Link to English version: Experimental and Analytical Investigation of the Load-Bearing Capacity of 3D Printed Concrete
In den letzten Jahren wurde 3D-gedruckter Beton (3DPC, von englisch “3D-printed concrete”) vorwiegend für nichttragende Anwendungen eingesetzt, etwa als Schalung für komplexe Geometrien oder hybride Bauteile, und seltener als wirklich tragendes Material. Das Hauptproblem liegt dabei darin, dass kein mechanisches Modell und keine damit einhergehende konsistente Bemessungsgrundlage für 3DPC existieren. Ein solches wurde aufgrund Unsicherheiten in der schichtweisen Herstellung und Herausforderungen bei der Bewehrungsintegration bislang noch nicht entwickelt. Durch den Druckprozess verhält sich 3DPC anisotrop: Die Festigkeit und Versagensmodi hängen nicht nur von der Betonmatrix ab, sondern auch von der Verbundqualität zwischen aufeinanderliegenden Schichten. Folglich lassen sich bestehende mechanische Modelle für konventionellen Beton nicht direkt auf 3DPC übertragen. Um 3DPC strukturell nutzen zu können, sind daher zuverlässige Prüfmethoden wie auch die Kenntnis von Versagenskriterien erforderlich. Damit kann eine Grundlage zur Bestimmung der Tragfähigkeit und zur Entwicklung eines konsistenten Bemessungsrahmens geschaffen werden. Um ein besseres Verständnis des Materialverhaltens unter verschiedenen Belastungszuständen zu ermöglichen, werden im Folgenden zwei an der ETH Zürich entwickelte Prüfmethoden präsentiert: der modifizierte Druckscherversuch und direkte Zugversuche an bewehrten 3D-gedruckten Beton-Zuggliedern.
Modifizierter Druckscherversuch
Der erste Versuch ist eine Modifikation des Druckscherversuchs, der bei konventionellem Beton eingesetzt wird, um den Verbund an Grenzflächen zu untersuchen, zum Beispiel zwischen zwei zu unterschiedlichen Zeitpunkten vergossenen Betonschichten oder zwischen Beton und Instandsetzungsmaterial (z.B. Klebstoffen). In diesem Versuch, gemäss EN 12615:1999, wird ein Prisma mit einer Grenzfläche, die in einem Winkel von ![]() = 60° zur Horizontalen geneigt ist, einer einachsigen Druckbelastung ausgesetzt.
= 60° zur Horizontalen geneigt ist, einer einachsigen Druckbelastung ausgesetzt.
Im Kontext von 3D-gedrucktem Beton wurde der modifizierte Druckscherversuch für die Bestimmung der wichtigsten Parameter des Materials 3DPC verwendet. Dies bedeutet, dass die Druckfestigkeit, die Kohäsion und der Reibungswinkel der Betonschichtgrenzfläche unter Berücksichtigung der durch die Schichtstruktur verursachten Anisotropie bestimmt wurden. Insgesamt wurden 45 Probekörper mit unterschiedlichen Aushärtezeiten (7, 14 und 28 Tagen nach dem 3D-Druck) geprüft. Jeder Probekörper bestand aus einem 400 mm hohen 3DPC-Prisma mit einem quadratischen Querschnitt (100 mm × 100 mm). Diese wurden mit unterschiedlichen Schichtneigungen (![]() = 0°, 30°, 60°, 75° und 90°) gedruckt, siehe Abbildung 1a. Um einen realistischen Unterbruch des 3D-Drucks abzubilden, wurde etwa auf halber Höhe des Prismas eine Kaltfuge (≈ 30 Min. Unterbruch) eingeführt. Nach Fertigstellung des Versuchskörpers kann er im Versuchsstand eingebaut werden. Dieser ist in Abbildung 1a dargestellt und besteht aus einer einachsigen Druckprüfung an den beschriebenen 3DPC-Prismen.
= 0°, 30°, 60°, 75° und 90°) gedruckt, siehe Abbildung 1a. Um einen realistischen Unterbruch des 3D-Drucks abzubilden, wurde etwa auf halber Höhe des Prismas eine Kaltfuge (≈ 30 Min. Unterbruch) eingeführt. Nach Fertigstellung des Versuchskörpers kann er im Versuchsstand eingebaut werden. Dieser ist in Abbildung 1a dargestellt und besteht aus einer einachsigen Druckprüfung an den beschriebenen 3DPC-Prismen.
Abbildung 1b zeigt die resultierende Spannungsverteilung auf horizontalen und geneigten Schnittebenen unter einer vertikalen Druckkraft (![]() ).
). ![]() bezeichnet die vertikale (normale) Spannung auf der Horizontalebene,
bezeichnet die vertikale (normale) Spannung auf der Horizontalebene, ![]() und
und ![]() bezeichnen die Normal- bzw. Schubspannungen in der Grenzfläche zwischen zwei gedruckten Schichten (Neigungswinkel
bezeichnen die Normal- bzw. Schubspannungen in der Grenzfläche zwischen zwei gedruckten Schichten (Neigungswinkel ![]() ). Diese Spannungen berechnen sich wie folgt:
). Diese Spannungen berechnen sich wie folgt:
(1) ![]()
wobei ![]() die effektive horizontale Fläche ist.
die effektive horizontale Fläche ist.

 und der auf der Schichtebene wirkenden Spannungen [1].
und der auf der Schichtebene wirkenden Spannungen [1]. Je nach Schichtneigung ![]() wurden zwei unterschiedliche Versagensarten beobachtet: (i) Matrixversagen oder (ii) Versagen der Schichtgrenzfläche. Probekörper, die mit Schichtneigungen von 0°, 30° und 90° gedruckt wurden, wiesen ein Matrixversagen auf, ähnlich wie bei konventionellem Beton (Abbildung 2a, b und e). Im Gegensatz dazu kann bei Schichtneigungen von 60° oder 75° die durch den Druckprozess verursachte Anisotropie zu vorzeitigem Versagen der Schichtgrenzfläche an der Kaltfuge führen (Abbildung 2c und d). Die Probekörper, die an der Schichtgrenzfläche versagten, wiesen im Vergleich zu denen mit Matrixversagen eine um etwa 10% bis 20% geringere Festigkeit auf.
wurden zwei unterschiedliche Versagensarten beobachtet: (i) Matrixversagen oder (ii) Versagen der Schichtgrenzfläche. Probekörper, die mit Schichtneigungen von 0°, 30° und 90° gedruckt wurden, wiesen ein Matrixversagen auf, ähnlich wie bei konventionellem Beton (Abbildung 2a, b und e). Im Gegensatz dazu kann bei Schichtneigungen von 60° oder 75° die durch den Druckprozess verursachte Anisotropie zu vorzeitigem Versagen der Schichtgrenzfläche an der Kaltfuge führen (Abbildung 2c und d). Die Probekörper, die an der Schichtgrenzfläche versagten, wiesen im Vergleich zu denen mit Matrixversagen eine um etwa 10% bis 20% geringere Festigkeit auf.

Basierend auf diesen Ergebnissen wurde eine allgemeine Umhüllende der Mohr’schen Kreise entwickelt, welche die Tragfähigkeit von 3DPC-Elementen unter Berücksichtigung der Schichtverbindungen charakterisiert. Das Modell kombiniert die modifizierte Coulomb-Fliessbedingung für die Betonmatrix mit einem Coulomb-Versagenskriterium für die Schichtverbindungen.
Die modifizierte Coulomb-Fliessbedingung der Betonmatrix wird aus den folgenden drei Grössen abgeleitet: (i) Der Durchschnitt der Spitzendruckspannung (![]() ) in den Probekörpern, die ein Matrixversagen aufweisen (
) in den Probekörpern, die ein Matrixversagen aufweisen (![]() = 0°, 30° und 90°), (ii) die Zugfestigkeit der Betonmatrix
= 0°, 30° und 90°), (ii) die Zugfestigkeit der Betonmatrix ![]() , und (iii) der Reibungswinkel
, und (iii) der Reibungswinkel ![]() und die Kohäsion
und die Kohäsion ![]() der Matrix. Diese können in den entsprechenden Mohrschen Kreisen eingezeichnet werden und sind gegeben durch:
der Matrix. Diese können in den entsprechenden Mohrschen Kreisen eingezeichnet werden und sind gegeben durch:
(2) 
Das Coulomb-Versagenskriterium für die Schichtgrenzen wurde aus den Probekörpern mit Schichtneigungen ![]() =60° und
=60° und ![]() =75° hergeleitet: Mittels linearer Regression wurde die folgende Formulierung aus den Spannungszuständen (
=75° hergeleitet: Mittels linearer Regression wurde die folgende Formulierung aus den Spannungszuständen (![]() und
und ![]() ) in der Schichtgrenzfläche bei der Spitzenbelastung abgeleitet:
) in der Schichtgrenzfläche bei der Spitzenbelastung abgeleitet:
(3) ![]()
wobei ![]() und
und ![]() jeweils der Reibungswinkel und der Kohäsionswinkel der Grenzfläche sind.
jeweils der Reibungswinkel und der Kohäsionswinkel der Grenzfläche sind.
Abbildung 3 zeigt die resultierenden allgemeinen Umhüllenden für 3DPC (Grenze der schraffierten Bereiche) im ebenen Spannungszustand mit kalten Fugen. In dieser Darstellung schneiden sich die Kurven der modifizierten Coulomb-Fliessbedingung der Betonmatrix und des Coulomb-Versagenskriteriums in den Punkten A und B. Diese entsprechen den kritischen Winkeln (![]() und
und ![]() ) und markieren den Übergang zwischen den unterschiedlichen Versagensmodi. Daher dominiert im modifizierten Druckscherversuch das Versagen der Schichtgrenzfläche, wenn die Schichtneigung innerhalb des kritischen Bereichs
) und markieren den Übergang zwischen den unterschiedlichen Versagensmodi. Daher dominiert im modifizierten Druckscherversuch das Versagen der Schichtgrenzfläche, wenn die Schichtneigung innerhalb des kritischen Bereichs ![]() liegt. Bei flacheren (
liegt. Bei flacheren (![]() ) oder steileren (
) oder steileren (![]() ) Schichtausrichtungen ist stattdessen ein Versagen der Matrix zu erwarten. In letzteren Fällen wird die Druckfestigkeit
) Schichtausrichtungen ist stattdessen ein Versagen der Matrix zu erwarten. In letzteren Fällen wird die Druckfestigkeit ![]() der Betonmatrix unter einachsiger Druckbeanspruchung erreicht, wie im modifizierten Druckscherversuch beobachtet. Umgekehrt versagt bei mittleren Neigungen innerhalb des kritischen Bereichs (
der Betonmatrix unter einachsiger Druckbeanspruchung erreicht, wie im modifizierten Druckscherversuch beobachtet. Umgekehrt versagt bei mittleren Neigungen innerhalb des kritischen Bereichs (![]() ) die Schichtgrenzfläche früher, was zu einer reduzierten Druckfestigkeit führt, die unter
) die Schichtgrenzfläche früher, was zu einer reduzierten Druckfestigkeit führt, die unter ![]() liegt. Der modifizierte Druckscherversuch bietet daher eine ideale Grundlage um Festigkeits- und Versagensmodi für verschiedene Neigungen der Schichtgrenzflächen von 3DPC festzustellen und darauf aufbauend die allgemeine Umhüllende der Mohr’schen Kreise für 3DPC zu bestimmen.
liegt. Der modifizierte Druckscherversuch bietet daher eine ideale Grundlage um Festigkeits- und Versagensmodi für verschiedene Neigungen der Schichtgrenzflächen von 3DPC festzustellen und darauf aufbauend die allgemeine Umhüllende der Mohr’schen Kreise für 3DPC zu bestimmen.

Die kritischen Schichtneigungen wurden mit ![]() = 60° und
= 60° und ![]() = 75° bestimmt, bei einem Grenzflächenreibungswinkel von etwa
= 75° bestimmt, bei einem Grenzflächenreibungswinkel von etwa ![]() = 46°. Abschliessend ist anzumerken, dass der 3DPC innerhalb von 14 Tagen nach dem 3D-Druck seine volle Druckfestigkeit – etwa 60 bis 80 MPa – erreichte und nach 7 Tagen etwa 80% dieser Festigkeit (55 bis 65 MPa) erreichte.
= 46°. Abschliessend ist anzumerken, dass der 3DPC innerhalb von 14 Tagen nach dem 3D-Druck seine volle Druckfestigkeit – etwa 60 bis 80 MPa – erreichte und nach 7 Tagen etwa 80% dieser Festigkeit (55 bis 65 MPa) erreichte.
Diese Ergebnisse zeigen, dass der modifizierte Druckscherversuch das anisotrope Verhalten von 3D-gedrucktem Beton effektiv erfassen kann und eine praktische Grundlage für die Entwicklung mechanischer Modelle und Sicherheitsfaktoren bietet. Weitere Forschung wird den Einfluss längerer 3D-Druckunterbrechungen untersuchen und den experimentellen Datensatz erweitern, um die vorgeschlagene allgemeine Umhüllende der Mohr’schen Kreise zu verfeinern. Ausführlichere Erläuterungen zu den Versuchsergebnissen finden Sie in [1].
Direkte Zugversuche an bewehrten 3DPC-Zuggliedern
Um 3DPC wirklich strukturell einsetzen zu können, müssen solche 3DPC-Elemente bewehrt werden. Die Bewehrung kann sowohl als Querbewehrung, die während des Drucks zwischen den Schichten angebracht wird, wie auch als Längsstab in den vergossenen Kanälen der 3D-gedruckten Schale angebracht werden, sodass das Element Zugspannungen sicher aufnehmen kann. Ergänzend zu den modifizierten Druckscherversuchen haben wir daher das Zugverhalten von bewehrten 3DPC-Zuggliedernuntersucht. Während das Zugverhalten von konventionellem Stahlbeton durch das Zuggurtmodell gut beschrieben werden kann, wurde dessen Anwendbarkeit auf 3DPC bisher nicht untersucht. Um diese Forschungslücke zu schliessen, wurde eine Pilotversuchsreihe durchgeführt, die sich auf das Zugverhalten von 3DPC konzentriert. Die Studie untersuchte den Einfluss verschiedener relevanter Parameter (Bewehrungsgehalt, lokale Querschnittsabweichungen aufgrund der Oberflächenstruktur der 3D-gedruckten Schichten, Inklusion von Querbewehrung (Bügel)) sowohl auf die Rissbildung als auch auf die Kraftübertragung zwischen den Materialien, aus denen die bewehrten 3DPC-Zugglieder bestehen. Das Ziel dieser Untersuchung war es, eine Grundlage für mechanisch konsistente Modelle zu schaffen, die die Strukturanalyse und den Entwurf von 3DPC-Elementen in zukünftigen Forschungsarbeiten unterstützen können.
3DPC-Zugglieder bestehen aus einer 3DPC-Hülle, in welche ein Stahlstab eingeführt wird und danach der restliche Zwischenraum mit Mörtel hinterfüllt wird. Das Zugverhalten und die Rissbildung eines solchen 3DPC-Zugglieds lassen sich analytisch durch ein Kräftegleichgewicht in einem idealisierten Zugstrang beschreiben (siehe Abbildung 4). Die Rissbildung liefert wertvolle Erkenntnisse, wie Zugkräfte vom Stahlstab über den Mörtelkern auf die 3DPC-Hülle übertragen werden. Die Rissbildung kann entweder in der 3DPC-Hülle oder im Mörtel beginnen, je nach Zugfestigkeit und Elastizitätsmodul der beiden Bestandteile. Wenn die Spannung nach dem ersten Materialriss weiter zunimmt, kann das zweite Material entweder nach einer weiteren Belastungserhöhung oder gleichzeitig mit dem ersten Material reissen. Daraus ergeben sich vier mögliche Rissbildungssequenzen (siehe Tabelle 1): (a1) Der 3DPC reisst zuerst, während der Mörtel unbeschädigt bleibt; (a2) der 3DPC und der Mörtel reissen gleichzeitig unter einer axialen Risslast (![]() ), die durch die 3DPC-Spannungen bestimmt wird; (b1) der Mörtel reisst zuerst, während der 3DPC unbeschädigt bleibt; und (b2) der Mörtel und der 3DPC reissen gleichzeitig unter einer axialen Risslast (
), die durch die 3DPC-Spannungen bestimmt wird; (b1) der Mörtel reisst zuerst, während der 3DPC unbeschädigt bleibt; und (b2) der Mörtel und der 3DPC reissen gleichzeitig unter einer axialen Risslast (![]() ), die durch die Mörtelspannungen bestimmt wird. Unter der Annahme eines linear-elastischen Verhaltens und einer starren Verbindung vor dem Reissen (gleiche Dehnung (
), die durch die Mörtelspannungen bestimmt wird. Unter der Annahme eines linear-elastischen Verhaltens und einer starren Verbindung vor dem Reissen (gleiche Dehnung (![]() ) in Stahl, Mörtel und 3DPC) kann die gesamte axiale Belastung vor dem Reissen (
) in Stahl, Mörtel und 3DPC) kann die gesamte axiale Belastung vor dem Reissen (![]() ) als Summe der axialen Kraftbeiträge jedes Materials formuliert werden:
) als Summe der axialen Kraftbeiträge jedes Materials formuliert werden: ![]() , wobei die Indizes
, wobei die Indizes ![]() ,
, ![]() und
und ![]() jeweils für 3DPC (engl. «concrete), Mörtel (engl. «mortar») und Stahl (engl. «steel») stehen. Tabelle 1 stellt eine Übersicht der wichtigsten Parameter zu den Rissbildungskriterien dar: die erste (
jeweils für 3DPC (engl. «concrete), Mörtel (engl. «mortar») und Stahl (engl. «steel») stehen. Tabelle 1 stellt eine Übersicht der wichtigsten Parameter zu den Rissbildungskriterien dar: die erste (![]() ) und zweite (
) und zweite (![]() ) Rissbildungslast, die entsprechenden Spannungen im Mörtel (
) Rissbildungslast, die entsprechenden Spannungen im Mörtel (![]() ) und 3DPC (
) und 3DPC (![]() ) nach dem ersten Riss und der Mindestbewehrungsgehalt (
) nach dem ersten Riss und der Mindestbewehrungsgehalt (![]() ), der erforderlich ist, um ein sprödes Versagen zu verhindern.
), der erforderlich ist, um ein sprödes Versagen zu verhindern.
Wenn ![]() (Szenarien a1 und a2) ist zu erwarten, dass der 3DPC zuerst reisst, andernfalls reisst der Mörtel zuerst (Szenarien b1 und b2). Unter der Annahme, dass
(Szenarien a1 und a2) ist zu erwarten, dass der 3DPC zuerst reisst, andernfalls reisst der Mörtel zuerst (Szenarien b1 und b2). Unter der Annahme, dass ![]() ist (eine vernünftige Schätzung), wird das abgeleitete Rissbildungskriterium in Tabelle 1 unter Szenario (a2) aufgeführt. Für diesen Fall besagt es, dass die Zugspannung des Mörtels seine Zugfestigkeit überschreitet, d.h. der Mörtel reisst unmittelbar nach dem 3DPC. Da der Mörtelanteil (
ist (eine vernünftige Schätzung), wird das abgeleitete Rissbildungskriterium in Tabelle 1 unter Szenario (a2) aufgeführt. Für diesen Fall besagt es, dass die Zugspannung des Mörtels seine Zugfestigkeit überschreitet, d.h. der Mörtel reisst unmittelbar nach dem 3DPC. Da der Mörtelanteil (![]() ) in der Regel gering ist, müsste dessen Zugfestigkeit um ein Vielfaches höher sein als die des 3DPC, um ein Reissen an derselben Stelle zu verhindern. Daraus folgt, dass Szenario (a1) in der Praxis seltener eintrifft. Daher gilt unter realistischen Konfigurationen:
) in der Regel gering ist, müsste dessen Zugfestigkeit um ein Vielfaches höher sein als die des 3DPC, um ein Reissen an derselben Stelle zu verhindern. Daraus folgt, dass Szenario (a1) in der Praxis seltener eintrifft. Daher gilt unter realistischen Konfigurationen:
- Wenn der 3DPC zuerst reisst, reisst der Mörtel gleichzeitig an derselben Stelle, da die Spannungen im Mörtel dort am höchsten sind, wo die 3DPC-Schale reisst (Szenario a2).
- Wenn der Mörtel zuerst reisst, bleibt der 3DPC möglicherweise kurzzeitig unbeschädigt (Szenario b1), reisst jedoch bald an derselben Stelle aufgrund der Spannungskonzentrationen, die sich in diesem Bereich entwickeln.


Jedes bewehrte 3DPC-Zugglied bestand aus einer konventionellen B500B-Stahlbewehrung, die in Mörtel eingebettet und von einer 3DPC-Hülle umgeben war. Die Versuchskörper waren 1.8 m lang, mit einem 1.44 m langen bewehrten 3DPC-Stab mit einem Querschnitt von 140 mm und einer 180 mm langen überstehenden Stange an jedem Ende. Der Mörtelkern hatte einen Durchmesser von 60 mm, die 3DPC-Hülle bestand aus 8 mm dicken und 40 mm breiten gedruckten Schichten (Abbildung 5b). Um den Einfluss des Bewehrungsgehalts zu untersuchen, wurden drei Proben mit Bewehrungsdurchmessern von Ø10, Ø12 und Ø14 mm verwendet, was einem Bewehrungsgehalt von 0.51%, 0.73% bzw. 1.00% entspricht. Zusätzlich wurden zwei Proben mit einem Bewehrungsdurchmesser von Ø12 mm an der Oberfläche abgeschliffen, um die Interpretation der Ergebnisse zu erleichtern und den Einfluss der gedruckten, unregelmässigen Oberflächenstruktur auf die DIC-Messungen (Digital Image Correlation) abschätzen zu können. Nur eine Probe wurde mit Querbewehrungsbügeln im Abstand von 240 mm versehen, alle anderen enthielten keine Querbewehrung. Abbildung 5c stellt eine Übersicht der Versuchsreihe dar, inklusive der Probebezeichnung mit der Prüfart (TC = Zugglied, von engl. «tension chord»), Nummer (1–5), Bewehrungsdurchmesser (D10, D12, D14), Oberflächenbehandlung (NG = nicht geschliffen, G = geschliffen) und Querbewehrung (S = Bügel, von engl. «stirrups»). Abbildung 5d zeigt den Versuchsaufbau für den direkten Zugversuch an bewehrten 3DPC-Verbindungselementen. Die Proben wurden in vertikaler Position platziert und an den Enden verformungsgesteuert einer axialen Zugbelastung ausgesetzt.
In dieser Versuchsreihe zeigen die Ergebnisse ein Verhalten, das mit Szenario (b1) übereinstimmt: Der Mörtel reisst zuerst (![]() ), während die 3DPC-Hülle zunächst unbeschädigt bleibt (Tabelle 1). Die Axialkraft, die erforderlich ist, um Risse im 3DPC zu verursachen, ist etwa 30% höher als die für den Mörtel erforderliche Axialkraft. Somit wurden die theoretischen Ergebnisse durch die Versuchsreihe mit fünf bewehrten 3DPC-Zuggliedern bestätigt, die unter Zugkraft bis zum Versagen getestet wurden.
), während die 3DPC-Hülle zunächst unbeschädigt bleibt (Tabelle 1). Die Axialkraft, die erforderlich ist, um Risse im 3DPC zu verursachen, ist etwa 30% höher als die für den Mörtel erforderliche Axialkraft. Somit wurden die theoretischen Ergebnisse durch die Versuchsreihe mit fünf bewehrten 3DPC-Zuggliedern bestätigt, die unter Zugkraft bis zum Versagen getestet wurden.


Die Prüfkörper wurden mit Digital Image Correlation (DIC) und Distributed Fibre Optic Sensing (DFOS) instrumentiert. DIC ermöglichte die kontinuierliche Messung von Verschiebungs- und Dehnungsfeldern auf der Oberfläche der 3DPC-Schale, während DFOS mithilfe integrierter Glasfasern quasi-kontinuierliche Dehnungsmessungen entlang der Bewehrungsstäbe lieferte, was die Untersuchung der Wechselwirkung zwischen der Bewehrung und dem umgebenden Mörtel erleichterte.
Abbildung 6 zeigt die Versuchsergebnisse bezüglich des Lastverformungsverhaltens, der Rissbildung und der durchschnittlichen Dehnungsentwicklung entlang der Probenlänge (T für oben (engl. «top») und B für unten (engl. «bottom») in Abbildung 6). Die Probe TC1_D10_NG wurde aus der Analyse ausgeschlossen, da ihr Bewehrungsgehalt ![]() unter dem Mindestwert
unter dem Mindestwert ![]() lag, was zu einer Filessengrenze vor der Rissbildung und somit zu einem spröden Versagen führte. Diese Konfiguration wurde nicht absichtlich gewählt und widerspiegelt praktische Einschränkungen, in diesem Fall die begrenzte Grösse der bewehrten 3DPC-Zugglieder, die eine Unsicherheit hinsichtlich der Zugfestigkeit des 3DPC hervorrief. Aus den anderen Experimenten lassen sich folgende Beobachtungen festhalten:
lag, was zu einer Filessengrenze vor der Rissbildung und somit zu einem spröden Versagen führte. Diese Konfiguration wurde nicht absichtlich gewählt und widerspiegelt praktische Einschränkungen, in diesem Fall die begrenzte Grösse der bewehrten 3DPC-Zugglieder, die eine Unsicherheit hinsichtlich der Zugfestigkeit des 3DPC hervorrief. Aus den anderen Experimenten lassen sich folgende Beobachtungen festhalten:
- Wie bei konventionellem Stahlbeton beeinflusst der Bewehrungsgehalt die Rissbildung: Höhere Bewehrungsgehalte führen zu geringeren Rissabständen und tragen dazu bei, das Fliessen bei Rissbildung zu verhindern (wie bei Probe TC2_D12_NG). Eine unzureichende Bewehrung führt zu wenig oder sogar keinen sichtbaren Rissen, wodurch die Verformungskapazität verringert wird (siehe auch durchschnittliche Dehnung der Probe TC2_D12_NG).
- Das Lastverformungsverhalten der bewehrten 3DPC-Zugglieder zeigte eine deutliche Zugversteifung, welchen man anhand der Parallelverschiebung der Kurven der bewehrten Proben (durchgezogene schwarze Kurve in Abbildung 6) und der nackten Stahlstange (gestrichelte graue Kurve in Abbildung 6) identifizieren kann.
- Die Bügel wirkten als lokale Schwachstellen und reduzierten den effektiven Querschnitt. Dadurch entstanden an diesen Stellen Risse und die Bildung einer konstanten Risslast wurde verhindert (siehe Probe TC4_D12_G_S).
- Die Oberflächenstruktur beeinflusste die Rissbildung: Geschliffene Proben entwickelten regelmässige Rissmuster bei konstanten Belastungsniveaus (siehe Probe TC3_D12_G), während ungeschliffene Proben unregelmässige Rissmuster aufwiesen und keine klare Plateauphase in der Lastverformungskurve zeigten (siehe Probe TC5_D14_NG).
- Korrelierte DIC- und DFOS-Messungen bestätigten eine effektive Zugkraftübertragung von Stahl auf Mörtel und 3DPC, wobei sich die Risse an derselben Stelle und fast gleichzeitig in beiden Materialien bildeten. Diese Beobachtungen werden durch die analytischen Ergebnisse gestützt und zeigen, dass nach dem Reissen des Mörtels der 3DPC zunächst kurzzeitig unbeschädigt bleiben kann, jedoch aufgrund von Spannungskonzentrationen schnell an derselben Stelle reisst. Auch bei nicht geschliffenen Proben konnten zuverlässige DIC-Daten erhoben werden, was bestätigt, dass die gedruckte Oberflächenstruktur die Messgenauigkeit nicht beeinträchtigte.

Diese Ergebnisse unterstreichen, dass das Zuggurtmodell mit den oben genannten Anpassungen auch für Bauteile aus 3DPC angewendet werden kann. Ausführlichere Erläuterungen zu den Versuchsergebnissen finden Sie in [2]. Die fünf erläuterten Experimente reichen jedoch noch nicht für eine vollständige Validierung des Zuggurtmodells aus. Deshalb werden in Kürze weitere Experimente durchgeführt. Bei Fragen dürfen Sie sich gerne direkt bei Lucia Licciardello melden.
Lucia Licciardello
Referenzen
- Licciardello L., Giraldo-Soto A., Kaufmann W., Metelli G. Determining the strength of 3D printed concrete with the modified slant shear test. Structural Concrete 2025;26:2467–86. https://doi.org/10.1002/suco.202400238.
- Licciardello L., Meillasson H., Giraldo-Soto A., Kaufmann W. Direct tensile tests on Reinforced 3D Printed Concrete ties, 4th fib Young Symposium 2025, Naples.
Link to English version: How accurate are current models for predicting reinforcement stresses under fatigue loads?
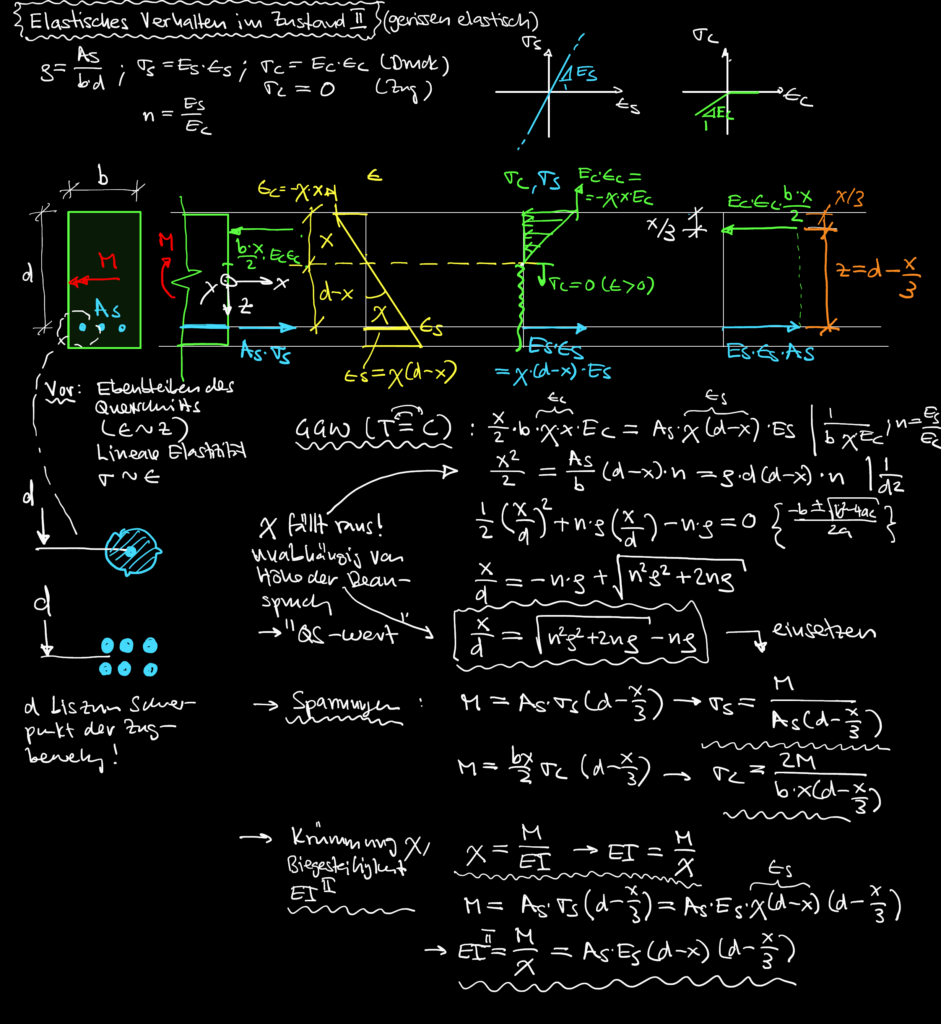
Um die Tragsicherheit von Brücken zu gewährleisten, ist neben dem Nachweis des Tragwiderstands auch der Nachweis der Ermüdungsfestigkeit erforderlich. Der Nachweis des Tragwiderstands ist gut erforscht und die entsprechenden Modelle (Normalmomenten-Fliessbedingung und Sandwich-Modell) sind in der Ingenieurpraxis etabliert. In diesen Modellen wird ein ausreichendes Verformungsvermögen angenommen und der Tragwiderstand unter Berücksichtigung von plastischen Umlagerungen ermittelt. Für den Ermüdungsnachweis und die zugehörige Ermittlung der Bewehrungsspannungen steht der Praxis bislang jedoch kein geeignetes Modell zur Verfügung. Gerade dieser Nachweis ist aber häufig für Fahrbahnplatten von Brücken massgebend. Unter Ermüdungslasten ist der Querschnitt der Fahrbahnplatte in der Regel gerissen, die Bewehrung fliesst jedoch noch nicht. Im Gegensatz zum Tragwiderstand sind für dieses komplexe, gerissen-elastische Tragverhalten keine plastischen Umlagerungen zulässig. Daher ist es wichtig, ein möglichst realitätsnahes Modell für Stahlbeton zu verwenden, das dieses Tragverhalten abbildet und somit eine zuverlässige Bestimmung der Bewehrungsspannungen ermöglicht.
Bei der Bemessung meiner ersten Brücke als Werkstudent wurde ich direkt mit diesem unbefriedigenden Zustand konfrontiert. Während ich die Nachweise des Tragwiderstands mit fachlicher Unterstützung und dem aus der Vorlesung erlernten Wissen führen konnte, fehlte ein geeignetes Modell, um die Spannungen der Bewehrung für den massgebenden Ermüdungsnachweis zuverlässig berechnen zu können. In diesem Blogbeitrag möchte ich deshalb die bestehenden Unsicherheiten bei der Anwendung des Ermüdungsnachweises für die Bewehrung zusammenfassen und anhand eines Vergleichs verschiedener Modelle zeigen, dass die in der Praxis gängigen Modelle dafür nicht geeignet sind. Im weiteren Verlauf des Blogbeitrags wird erläutert, wie ein Forschungsprojekt in Zusammenarbeit mit dem Bundesamt für Strassen (ASTRA) diese Unsicherheiten adressiert und wie damit verbundene zurzeit ungenutzte Reserven zusätzlich ausgeschöpft werden können. Ziel ist es, unnötige Verstärkungsmassnahmen zu vermeiden, Ressourcen zu schonen und damit aus einer planerischen Perspektive einen Beitrag zur Entlastung der Umwelt zu leisten.
Die oben beschriebenen Unsicherheiten für den Ermüdungsnachweis der Bewehrung können in zwei Kategorien zusammengefasst werden und sind in Abbildung 1 illustriert:
(i) Die Bestimmung der Schnittkräfte in der Fahrbahnplatte unter Ermüdungslasten
{nx, ny, nxy, mx, my, mxy, vx, vy}
(ii) Die Berechnung der daraus resultierenden Bewehrungsspannungen
{σsrx,inf, σsrx,sup, σsry,inf, σsry,sup}

(i) Bestimmung der Schnittkräfte unter Ermüdungslasten
Die Schnittkräfte in der Fahrbahnplatte infolge von Ermüdungslasten (siehe Abbildung 1 (i)) werden in der Praxis in der Regel mit linear-elastischen Finite Elemente Analysen (lineare FEA) bestimmt. Solche Berechnungen sind in verbreiteten Programmen wie Cubus oder Axis einfach anzuwenden und benötigen nur kurze Rechenzeiten. Im Gegensatz zu den numerisch aufwendigeren und zeitintensiveren nichtlinearen Finite-Elemente-Analysen (NLFEA) kann die lineare FEA jedoch das Verhalten des gerissen-elastischen Stahlbetonquerschnitts nicht abbilden. Für den Ermüdungsnachweis relevant sind dabei insbesondere die mit der Rissbildung verbundenen Druckmembranspannungszustände. Durch das Reissen des Querschnitts dehnt sich die Fahrbahnplatte bezüglich ihrer Mittelebene aus. Diese Ausdehnung wird durch steifere Bauteile wie beispielsweise Brückenstege eingeschränkt (siehe Abbildung 2 (a)), wodurch der zuvor erwähnte Druckmembranspannungszustand in der Fahrbahnplatte entsteht (siehe Abbildung 2 (b)). Wie der Name andeutet, erzeugt dieser Zustand Druckkräfte in der Ebene der Fahrbahnplatte, die die Spannungen in der Bewehrung reduzieren. Je stärker diese Ausdehnung behindert wird (grössere Federsteifigkeiten k in Abbildung 2 (b)), desto ausgeprägter ist die Spannungsreduktion in der Bewehrung. Bereits eine leicht eingeschränkte Ausdehnung kann zu einer deutlichen Verringerung der Bewehrungsspannungen führen. Um diese Reserven ausschöpfen zu können, muss für die Bestimmung der Schnittkräfte daher eine NLFEA verwendet werden, die diese Membranspannungszustände zuverlässig abbilden kann.

(ii) Ermittlung der resultierenden Bewehrungsspannungen
Selbst wenn die Schnittkräfte aus einer linearen FEA übernommen werden, gibt es kein praxistaugliches und experimentell validiertes Verfahren, um die resultierenden Spannungen in der Bewehrung zu ermitteln (siehe Abbildung 1 (ii)). In der Praxis werden häufig die Normalmomenten-Fliessbedingung (siehe Gleichungen in Abbildung 3 (a)) oder das Sandwich-Modell (siehe Abbildung 3 (b)) verwendet, um aus den linear-elastisch ermittelten Schnittkräften die Spannungen in der Bewehrung zu ermitteln. Diese Modelle nehmen jedoch plastische Umlagerungen an und sind somit nicht zulässig für die Ermittlung der Bewehrungsspannungen durch Ermüdungslasten.

In der Forschung gibt es durchaus Modelle, die auch das für die Ermüdung relevante gerissen-elastische Tragverhalten von Stahlbeton abbilden können. In der Regel werden dazu sogenannte Schichtenmodelle (beispielsweise CMM-Usermat in Abbildung 3 (c)) verwendet. Die Grundidee ist dabei ähnlich wie bei Spannungsberechnungen am Balken: Es wird angenommen, dass die jeweiligen Dehnungen linear über die Höhe des Querschnitts variieren. Das Element wird in mehrere Schichten unterteilt, die nur über die vorhergehende Annahme miteinander verknüpft werden. Unter der weiteren Annahme, dass jede Schicht einen ebenen Spannungszustand aufweist, können ausgehend von den Dehnungen jeder Schicht die zugehörigen Spannungszustände jeder Schicht ermittelt werden. Mittels Integration über die Schichten können dann die resultierenden Schnittgrössen ermittelt werden. Das an der Professur verfügbare CMM-Usermat [3], das auf dem mechanisch konsistenten Cracked Membrane Model (CMM) [4] basiert, ist ein solches Schichtenmodell. Da das Modell die Zugversteifung über das Zuggurtmodell berücksichtigt, sollte es die Ausdehnung der Mittelebene bei Rissbildung realitätsnah erfassen und damit auch die Druckmembrankräfte des Membranspannungszustands zuverlässig abbilden können. Das CMM-Usermat wurde in die kommerzielle Software ANSYS implementiert und ist bereits ausführlich mit Experimenten hinsichtlich des globalen Last-Verformungsverhaltens validiert worden. Für eine Überprüfung der resultierenden Bewehrungsspannungen und der zuvor beschriebenen grundlegenden Annahmen des Schichtenmodells stehen jedoch nicht genügend experimentelle Daten zur Verfügung.
In einem früheren Blogbeitrag hat Vera Balmer bereits die Entwicklung eines hybriden Machine-Learning-FE-Ansatzes vorgestellt, der ebenfalls auf diesem Schichtenmodell basiert. Zudem haben Balmer et al. [5] mit dem Schichtenmodell (CMM-Usermat) gezeigt, wie schon eine gering eingeschränkte Ausdehnung der Mittelebene κ die Bewehrungsspannungen erheblich reduziert (siehe Abbildung 4). Zusätzlich haben sie die mit dem CMM-Usermat ermittelten Bewehrungsspannungen mit denen verglichen, die sich aus der Normalmomenten-Fliessbedingung (NMYC) ergeben. Der Vergleich zeigt, dass die Normalmomenten-Fliessbedingung über weite Strecken von κ zu konservativ ist. Für kleine Werte von κ können die damit ermittelten Bewehrungsspannungen aber auch auf der unsicheren Seite liegen, wie in Abbildung 4 anhand von ρ = 1 dargestellt.

ASTRA-Forschungsprojekt zur Bestimmung der Bewehrungsspannungen unter Ermüdungslasten
Das ASTRA-Forschungsprojekt setzt bei beiden zuvor beschriebenen Unsicherheiten an: (i) Bestimmung der Schnittkräfte unter Ermüdungslasten und (ii) Ermittlung der resultierenden Bewehrungsspannungen. Zunächst sollen acht grossmassstäbliche Scheibenelementversuche im Large Universal Shell Element Tester (LUSET) durchgeführt werden, um mit geeigneten Lastkombinationen die grundlegenden Ansätze des Schichtenmodells und die daraus resultierenden Bewehrungsspannungen zu validieren. Das validierte Modell soll danach praktizierenden Ingenieur:innen zur Verfügung gestellt werden, damit sie aus linear-elastisch ermittelten Schnittkräften die resultierenden Bewehrungsspannungen zuverlässig berechnen können.
Im nächsten Schritt wird ein stufenweises Verfahren für die Ermüdungsbemessung der Bewehrung erarbeitet das der Praxis ebenfalls schlussendlich zur Verfügung gestellt wird. Ziel des Verfahrens ist es, die Reserven aus Druckmembranspannungszuständen (Abbildung 2) gezielt zu berücksichtigen. Dazu werden auf Basis des validierten Schichtenmodells mittels NLFEA die Schnittkräfte inklusive der vorteilhaften Druckmembranspannungszustände ermittelt. Die daraus resultierenden Bewehrungsspannungen werden mit denjenigen verglichen, die aus den linear-elastisch bestimmten Schnittkräften unter Verwendung des Schichtenmodells bestimmt wurden. Auf dieser Grundlage kann dann abgeschätzt werden, unter welchen Bedingungen die Reserven aus Druckmembranspannungszuständen tatsächlich genutzt werden können.
Zusätzlich zu den acht vom ASTRA-Forschungsprojekt finanzierten Versuchen wurden im vergangenen Jahr im Rahmen eines weiteren Projekts bereits zwei LUSET-Versuche durchgeführt. Diese Tests umfassten eine allgemeine Belastung mit Membrandruck- und Membranschubkräften sowie Querbiegung und Torsion. Bevor daraus erste Schlüsse für das Schichtenmodell und die folgenden LUSET-Versuche gezogen werden können, müssen die experimentellen Daten jedoch noch vollständig ausgewertet werden.
Die Ergebnisse der beiden zusätzlichen Tests werden hier zu einem späteren Zeitpunkt präsentiert. In den kommenden Jahren werden zudem die Resultate der weiteren LUSET-Versuche zur Erforschung des Tragverhaltens von Stahlbetonschalen im gerissen-elastischen Zustand und zur Ermittlung der Bewehrungsspannungen für den Ermüdungsnachweis erarbeitet und in späteren Blogposts oder Studien veröffentlicht.
Yannick Kummer
Referenzen
- K. Thoma, A. Kenel, G. Borkowski, “Ermüdung von vorwiegend auf Biegung beanspruchter Fahrbahnplatten”, Forschungsprojekt AGB 2010/001.
- W. Kaufmann, Lecture Notes Advanced Structural Concrete 2025, Chapter 5.2: Slabs–Yield conditions.
- K. Thoma, “Finite element analysis of experimentally tested RC and PC beams using the cracked membrane model”, Engineering Structures 167 (2018) 592-607.
- W. Kaufmann and P. Marti, ‘Structural Concrete: Cracked Membrane Model’, Journal of Structural Engineering, vol. 124, no. 12, pp. 1467–1475, 1998, doi: 10.1061/(ASCE)0733-9445(1998)124:12(1467).
- V. Balmer, K. Thoma, W. Kaufmann, “Design of Concrete Shells and Plates: A Solved Problem?”, IASS 2024, https://doi.org/10.3929/ethz-b-000698486.
Link to English version: Beauty of Experimental Research with LUSET
Die Schönheit experimenteller Forschung – mit LUSET
Hinweis: In diesem Beitrag teile ich meine Gedanken zur experimentellen Forschung im Bereich des konstruktiven Ingenieurbaus – basierend auf meinen Erfahrungen an der ETH Zürich. Andere Bereiche der experimentellen Forschung – insbesondere solche mit Tierversuchen – sind nicht Teil dieses Blogbeitrags.
Ich erinnere mich noch gut an mein erstes Gespräch mit Prof. Walter Kaufmann. Wir hatten einen Videoanruf und sprachen über das Forschungsvorhaben, für das ich mich beworben hatte. Irgendwann fragte er mich, ob ich Erfahrung mit experimenteller Forschung hätte. Meine Antwort war „jayn“ – eine Mischung aus ja und nein auf Deutsch – denn ich wusste nicht wirklich, was auf mich zukommt.
Was ist experimentelle Forschung?
Wozu dient sie? Warum brauchen wir sie im konstruktiven Ingenieurbau? Wie funktioniert sie? Welche Geräte sind dafür notwendig?
Wenn Du Dir diese Fragen stellst, erkläre ich Dir kurz die Prinzipien der experimentellen Forschung – und wie (und warum) wir sie in unserem Fachgebiet anwenden.
Experimentelle Forschung ist ein systematischer, wissenschaftlicher Ansatz, bei dem Forschende gezielt eine oder mehrere Variablen eines betrachteten Objekts verändern – mithilfe spezieller Versuchsanlagen, Maschinen oder Methoden. Idealerweise wird dabei immer nur eine Variable verändert, um klare und vergleichbare Ergebnisse zu erhalten.
Stell Dir vor, Du bist Koch in einem Sternerestaurant und willst ein neues Gericht perfektionieren. Du kochst es hundert Mal – aber jedes Mal veränderst Du nur eine Zutat, und beobachtest das Ergebnis. Einmal gibst Du 5 Gramm Salz hinzu, das nächste Mal 8 Gramm – bis Du am Ende das perfekte Spaghetti aglio e olio servierst.
Im Bauingenieurwesen geht es bei der experimentellen Forschung oft darum, das Tragverhalten von Materialien und Tragwerken unter verschiedenen Lasten zu verstehen. Das Spektrum reicht von kleinen Materialproben – wie z. B. Beton-Zylindern – bis hin zu grossen Bauteilen wie Balken, Stützen oder sogar Brückensegmenten in Originalgrösse. Ziel ist es, das reale Tragverhalten abzubilden, theoretische Modelle zu validieren und Entwurfsansätze zu verbessern.
Beispielsweise werden Versuche durchgeführt, um zu untersuchen, wie sich eine Betonschale unter kombinierter Biege- und Membrankraft verformt – oder wie ein Brückenträger auf Erdbebenbelastung reagiert. Diese Versuche liefern wichtige Daten zur Verbesserung numerischer Simulationen, zur Weiterentwicklung von Normen und zur Erhöhung der Sicherheit unserer Bauwerke.
In Fächern wie Medizin, Chemie oder Physik ist es oft einfacher, einzelne Variablen isoliert zu betrachten. Im konstruktiven Ingenieurbau ist das meist komplexer. Deshalb gilt: Ohne die richtige Ausrüstung kannst Du keine klaren und aussagekräftigen Experimente durchführen.
Fast jedes Institut für konstruktiven Ingenieurbau auf der Welt hat Labore – aber deren Qualität und Ausstattung sind sehr unterschiedlich. Das wirkt sich direkt auf die Forschungskapazität und den wissenschaftlichen Einfluss einer Universität aus. Genau das ist einer der vielen Gründe, warum das Bauingenieurwesen an der ETH Zürich auf Platz zwei der Weltrangliste steht [1] – und meiner Meinung nach das beste Labor für experimentelle Forschung in unserem Bereich hat.
Die Bauhalle
Als ich zum ersten Mal die Bauhalle – das experimentelle Forschungslabor der ETH Zürich in IBK – betreten habe, fühlte ich mich wie ein Kind im LEGOLAND. Der Raum selbst ist beeindruckend: 120 Meter lang, 30 Meter breit, 12 Meter hoch. Aber noch wichtiger als die Grösse sind die Versuchsaufbauten darin.
Ich will an dieser Stelle nicht zu sehr ins Detail gehen – mehr Infos findest Du hier [2] – aber ich kann Dir sagen: Diese Halle hat fast alles, was ein Labor im konstruktiven Ingenieurbau haben kann. Und darüber hinaus gibt es dort auch spezielle Prüfeinrichtungen wie LUSET und MAST.
In diesem Beitrag geht es aber vor allem um LUSET – der Large Universal Shell Element Tester [3].
LUSET
Seitdem ich an der ETH Zürich arbeite, verbringe ich den Grossteil meiner Zeit mit LUSET. Ich habe es schon so vielen Menschen vorgestellt, dass ich gar nicht mehr mitzählen kann. Wer mich in Zürich besucht, sieht zuerst LUSET – und erst danach den Rest der Stadt.
Auch die Bauhalle selbst bekommt regelmässig Besuch. Tatsächlich gehört eine Führung durch das Labor zu fast jedem Event des IBK. Ich kann mit Sicherheit sagen: Über 50-60 % der Besucher:innen sind fachfremd –aber trotzdem total begeistert, wenn sie LUSET sehen. Und sie stellen immer ähnliche Fragen, zum Beispiel:
Was ist ein Schalenelement?
Kurz erklärt: Tragwerke lassen sich nach ihrer Geometrie und ihrem Tragverhalten einteilen:
• Eindimensional: Stabtragwerke
• Zweidimensional: Flächentragwerke
• Dreidimensional: Volumentragwerke
Zweidimensionale Tragwerke lassen sich weiter unterteilen:
• Platten: durch senkrechte (aus der Ebene) Lasten beansprucht (z. B. Deckenplatten)
• Scheiben: durch Lasten in der Ebene beansprucht (z. B. Wände)
• Schalen: sowohl in der Ebene als auch aus der Ebene beansprucht (z. B. Kuppeln, gewölbte Dächer)
Jede dieser Tragwerksarten basiert auf unterschiedlichen Berechnungstheorien und hat unterschiedliche Freiheitsgrade – mit unterschiedlicher Komplexität.
Was macht LUSET?
Wie oben schon kurz erklärt, sind Schalenelemente die komplexeste Art von Flächentragwerken. Um sie gleichzeitig in- und aus der Ebene zu beanspruchen – und das noch im grossen Massstab – braucht es eine hochpräzise und technisch aufwendige Versuchseinrichtung.
Und genau das ist LUSET. Die Anlage hat 80 hydraulische Aktuatoren in der Ebene und 20 Aktuatoren aus der Ebene – insgesamt also 100 Aktuatoren, verteilt auf vier Quadranten (20 + 5 pro Quadrant). Damit kann LUSET Kräfte von bis zu 30 MN (3000 Tonnen) in Druck, 22 MN in Zug und 11 MN in reiner Schubkraft aufbringen – und noch mehr [4]. Theoretisch lässt sich jede mögliche Lastkombination, die ein Schalenelement erfahren könnte, simulieren.
Meine Erfahrungen mit LUSET
Das erste Projekt mit LUSET war der Test von Mauerwerkswänden unter zweiaxialer Belastung [5]. Es war das erste Mal, dass mit LUSET eine Mauerwerkswand getestet wurde. Um die Wand in die Testeinrichtung zu bekommen, mussten wir ein spezielles Montagesystem entwerfen. Besonders die Einspannung der Probe in LUSET und die präzise Krafteinleitung erforderten neue Ansätze und höchste Vorsicht, damit nichts beschädigt wird.

Das zweite Projekt ist Teil meiner aktuellen Doktorarbeit. Wir untersuchen die Rahmeneckbewehrungen von Rahmenbrücken im Eisenbahnverkehr – mit Fokus auf die Ermüdungsfestigkeit. Dafür haben wir die Rahmeneckbewehrungen mit faseroptischen Sensoren entlang der Bewehrung ausgestattet, um die Dehnungen detailliert zu erfassen. Insgesamt testen wir vier Probekörper – jeweils mit unterschiedlicher Geometrie und Bewehrungsführung an den Ecken – um den Einfluss dieser Parameter auf das Ermüdungsverhalten zu analysieren.

Eine Testeinrichtung – von 15 cm dicken Mauerwerkswänden bis hin zu grossmassstäblichen Rahmenbrücken… Jedes Projekt bringt neue Herausforderungen und neue Ansätze mit sich.
Die Schönheit experimenteller Forschung mit LUSET
Wenn Du jetzt weisst, was experimentelle Forschung im konstruktiven Ingenieurbau bedeutet – und was LUSET leisten kann – dann erkennst Du schnell, wie schön die Arbeit mit so einer Anlage sein kann.
Es geht nicht nur darum, eine riesige Maschine zu bedienen. Es geht darum, sinnvolle Fragestellungen zu beantworten, kreative Versuchsaufbauten zu entwickeln und aus den Ergebnissen zu lernen – ob sie nun Deinen Erwartungen entsprechen oder Dich komplett überraschen.
Fazit
In den letzten 16 Monaten an der ETH Zürich im kfmResearch Group habe ich den Grossteil meiner Zeit in der Bauhalle verbracht – ich habe neue Fähigkeiten gelernt, mich mit Kolleg:innen aus anderen Forschungsgruppen ausgetauscht und unzählige Tests beobachtet. Jeder Tag in der Bauhalle ist eine neue Gelegenheit, etwas dazuzulernen und Lösungen für komplexe ingenieurtechnische Probleme zu finden.
Und ehrlich gesagt: Wenn mich heute nochmal jemand fragt, ob ich Erfahrung mit experimenteller Forschung habe, würde ich immer noch „jayn“ sagen – denn man hat nie genug Erfahrung. Genau deshalb trägt dieser Beitrag den Titel Die Schönheit experimenteller Forschung mit LUSET.
Zum Schluss möchte ich allen danken, die mich auf diesem Weg begleitet haben – in und ausserhalb der Bauhalle. Ein besonderer Dank geht an das Bauhallen-Team und an alle meine studentischen Assistent:innen während dieser Zeit.
Und natürlich: Experimentelle Forschung hat auch ihre Schattenseiten. Es ist nicht immer einfach. Aber wir Ingenieur:innen kennen das ja – die Sinuskurve gehört dazu. Mit ihren Hochs und Tiefs…
Caglar Onbasi
Referenzen
- Mickein, Iris: ETH Zürich weltweit auf Platz 2 in Bauingenieurwissenschaften – https://baug.ethz.ch/news-und-veranstaltungen/news/2025/03/eth-zuerich-ist-die-weltbeste-hochschule-in-erdwissenschaften-und-geophysik.html
- Experimentelle Forschung (expRES@IBK) https://ibk.ethz.ch/de/forschung/ResearchFT.html
- The Large Universal Shell Element Tester (LUSET) – https://kaufmann.ibk.ethz.ch/de/forschung/ausgewaehlte-forschungsprojekte/LUSET.html
- Kaufmann, Walter; Beck, Alexander; Karagiannis, Demis; Werne, Dominik: The Large Universal Shell Element Tester – https://doi.org/10.3929/ethz-b-000379657
- Weber, Marius: «Einrichtung einer hochschulübergreifenden Gruppe für Forschung und Lehre im Bereich des konstruktiven Mauerwerkbaus» – https://concrete.ethz.ch/blog/einrichtung-einer-hochschuluebergreifenden-gruppe-fuer-forschung-und-lehre-im-bereich-des-konstruktiven-mauerwerkbaus/
Link to English version: Threaded stainless-steel rods: Relaxation and application in post-tensioning
Hochfeste Duplex-Gewindestangen (aus nichtrostendem Stahl) könnten eine Lösung für die externe Vorspannung von Bauteilen bei Neubauten oder zur Verstärkung bestehender Bauwerke darstellen. Der Mangel an verlässlichen Daten über die Relaxation von Stäben aus nichtrostendem Stahl schränkt jedoch ihre Verwendung als Vorspannung ein. Die Abschätzung der Relaxation ist entscheidend für die Verwendung von Stäben zur Vorspannung. Im Fall von nichtrostendem Stahl gewinnt sie sogar noch grössere Bedeutung, da die maximale Anfangsdehnung, die durch das Vorspannen erzeugt wird, deutlich geringer ist als bei konventionellem Spannstahl – sie beträgt nur etwa 50 % im Vergleich zu Y1860-S7. Ursache dafür ist die Begrenzung der Dehnung durch (i) die niedrigere Streckgrenze (![]() < 1’000 MPa gegenüber
< 1’000 MPa gegenüber ![]() > 1’000 MPa bei typischen Vorspannstählen) und (ii) die in SIA 263:2013 [1] definierte Bemessungszugfestigkeit von Gewindestangen (als Schrauben betrachtet):
> 1’000 MPa bei typischen Vorspannstählen) und (ii) die in SIA 263:2013 [1] definierte Bemessungszugfestigkeit von Gewindestangen (als Schrauben betrachtet):
(1) ![]()
wobei ![]() : Bemessungszugfestigkeit der Gewindestange;
: Bemessungszugfestigkeit der Gewindestange; ![]() : Zugfestigkeit der Gewindestange;
: Zugfestigkeit der Gewindestange; ![]() : Nettofläche der Gewindestange; und
: Nettofläche der Gewindestange; und ![]() : Widerstandsbeiwert für Verbindungsmittel und Nachweise im Nettoquerschnitt (
: Widerstandsbeiwert für Verbindungsmittel und Nachweise im Nettoquerschnitt (![]() = 1.25).
= 1.25).
Die Begrenzung der Vorspannkraft spielt eine grössere Rolle bei vorgespannten Bauteilen, die Zwangsverformungen (z. B. Kriechen und Schwinden) ausgesetzt sind, da die Spannkraftverluste in solchen Fällen unzulässige Werte erreichen können. Die nachstehende Tabelle vergleicht die Spannkraftverluste in Form von Dehnungen zwischen nichtrostenden Duplexstählen und dem Stahl Y1860 unter Verwendung typischer Konstruktions- und Werkstoffeigenschaften. Wird ein vorgespanntes Betonelement mit Duplex-Gewindestangen betrachtet und von den unten angegebenen Werten für Materialeigenschaften und Vorspannung ausgegangen, so betragen die Vorspannverluste 27% und liegen damit fast doppelt so hoch wie bei Y1860-Stahl (15%). Da hohe Spannkraftverluste gemäss SIA 262:2013 [2], welche die minimale Vorspannung nach Verlusten bei unendlicher Zeit auf 0.45·![]() begrenzt, unzulässig sein können, ergibt sich die Notwendigkeit, die Spannkraftverluste zu kontrollieren. Dies kann erreicht werden, indem die Relaxation der Duplex-Gewindestangen bekannt ist und die Vorspannkraft gezielt ausgenutzt wird (
begrenzt, unzulässig sein können, ergibt sich die Notwendigkeit, die Spannkraftverluste zu kontrollieren. Dies kann erreicht werden, indem die Relaxation der Duplex-Gewindestangen bekannt ist und die Vorspannkraft gezielt ausgenutzt wird (![]() ≥ 0.75·
≥ 0.75·![]() , d.h. eine Überschreitung der Bemessungszugfestigkeit nach Gl. (1).
, d.h. eine Überschreitung der Bemessungszugfestigkeit nach Gl. (1). ![]() ist die Anfangszugspannung des Spannstahls).
ist die Anfangszugspannung des Spannstahls).
| Beton | |||||
| 30 | Elastizitätsmodul | ||||
| 0.35 | Schwindmass | ||||
| 2.0 | Kriechzahl | ||||
| 5.0 | Anfangsspannungen | ||||
| 0.17 | Anfangsdehnung | ||||
| 0.33 | Langfristige Dehnungszunahme | ||||
| Duplex-Edelstahl | Stahl Y1860-S7 | ||||
| 160 | 195 | Elastizitätsmodul | |||
| 800 | 1860 | Zugfestigkeit / charakteristische Zugfestigkeit | |||
| 700 | 1640 | Streckgrenze / 0.1 %-Dehngrenze (charakteristisch) | |||
| 1.25 | 1.15 | Teilsicherheitsbeiwert | |||
| 576 | 1617 | Bemessungswert der Zugfestigkeit | |||
| 560 | 1302 | Anfangsvorspannung | |||
| 3.50 | 6.68 | Anfangsdehnung | |||
| 7.5% | 5% | Relaxation (Verlustquote der Vorspannung) | |||
| 27% | 15% | ||||
| (1) | |||||
| (2) | |||||
Zur Beurteilung des Vorspannpotenzials von hochfesten Duplex-Gewindestangen (nichtrostender Stahl) werden in diesem Beitrag die Ergebnisse einer Versuchskampagne zum Relaxationsverhalten von M24-, M27- und M30-Stäben vorgestellt. Die Relaxation wurde gemäss ISO 15630-3:2019 [3] über einen Zeitraum von 1’000 Stunden gemessen. Die Studie untersuchte auch, ob theoretische Modelle für Spannstahl die Langzeitrelaxation anhand kürzerer 120-Stunden-Versuche an Duplex-Gewindestangen zuverlässig vorhersagen können. Die Versuchsreihe wurde im Jahr 2023 in der Bauhalle der ETH Zürich durchgeführt und umfasste neun Relaxationsversuche (drei Proben pro Stangengrösse) an M24-, M27- und M30-Duplex-Gewindestangen. Zusätzliche Zugversuche (hier nicht im Detail aufgeführt) wurden an Stäben ohne vorherige Belastungsgeschichte sowie nach den Relaxationsversuchen durchgeführt, um die Veränderung der mechanischen Eigenschaften des Materials zu beurteilen.
Experimentelle Kampagne
Die Bezeichnungen und Eigenschaften der Proben sind in Tabelle 2 zusammengestellt. Alle Proben sind Gewindestangen aus hochfestem Duplexstahl (EN 1.44621Die Werkstoffeigenschaften von hochfestem Duplex EN 1.4462 gemäss der technischen Produktdokumentation der Leviat AG [4] sind wie folgt: Streckgrenze ![]() ≥ 700 MPa, Zugfestigkeit:
≥ 700 MPa, Zugfestigkeit: ![]() ≥ 900 MPa und Bruchdehnung:
≥ 900 MPa und Bruchdehnung: ![]() = 15‰ – 30‰). Um eine konstante Spannungs-Dehnungs-Kurve zu erhalten, wurden Duplex-Stäbe mit durchgehendem Gewinde gewählt. Bei Stäben mit durchgehendem Gewinde wird eine höhere Vorspannkraft (oder Dehnung) erreicht als bei Stäben, die nur im Verankerungsbereich mit einem Gewinde versehen sind (die maximale Vorspannung wird durch die Gewindebereiche begrenzt, wobei die Kapazität der gewindelosen Bereiche nicht ausgenutzt wird).
= 15‰ – 30‰). Um eine konstante Spannungs-Dehnungs-Kurve zu erhalten, wurden Duplex-Stäbe mit durchgehendem Gewinde gewählt. Bei Stäben mit durchgehendem Gewinde wird eine höhere Vorspannkraft (oder Dehnung) erreicht als bei Stäben, die nur im Verankerungsbereich mit einem Gewinde versehen sind (die maximale Vorspannung wird durch die Gewindebereiche begrenzt, wobei die Kapazität der gewindelosen Bereiche nicht ausgenutzt wird).
| ID (1) | Grösse | Material | [mm] | Querschnitt (2) (effektiv) [mm2] | Gesamtlänge [mm] | [kN] |
| SX-M24-r | M24 | EN 1.4462 | 24 | 353 | 1800 | 229 |
| SX-M27-r | M27 | EN 1.4462 | 27 | 459 | 1800 | 297 |
| SX-M30-r | M30 | EN 1.4462 | 30 | 561 | 1800 | 364 |
| (1) SX: Probe S1, S2 und S3; r: “Relaxationsprüfungen” | ||||||
| (2) Gemäss der technischen Produktdokumentation [4] | ||||||
| (3) Durch Anwendung der Gl. (1) | ||||||
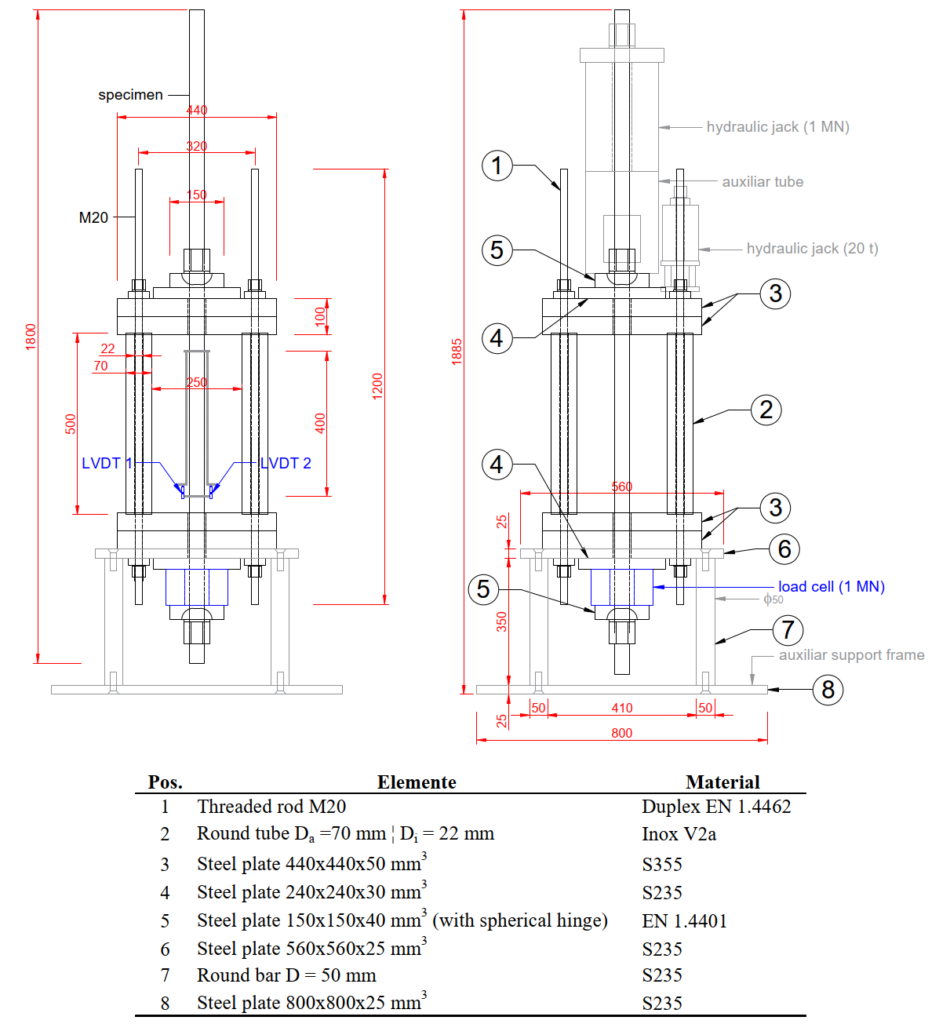
Abbildung 1 gibt einen Überblick über den an der ETH Zürich entwickelten Prüfstand zur Durchführung von Relaxationsprüfungen an Gewindestangen nach ISO 15630-3:2019. Der Prüfstand besteht aus einem Hauptrahmen (Pos. 1, 2 und 3), einem Stützrahmen (Pos. 6, 7 und 8), Verankerungsplatten (Pos. 4 und 5) und Messgeräten (zwei LVDT und eine Kraftmessdose).
Relaxation nach 1’000 Stunden
Die Relaxationsversuche an Duplex-Gewindestangen (M24, M27 und M30) wurden nach 1’000 Stunden mit einer Vorspannung (![]() ) durchgeführt, die zwischen 0.72 und 0.82 der durchschnittlichen Zugfestigkeit (
) durchgeführt, die zwischen 0.72 und 0.82 der durchschnittlichen Zugfestigkeit (![]() ) lag, welche Zugfestigkeit aus den Zugversuchen an Stäben ohne vorherige Belastungsgeschichte ermittelt wurde (siehe den Durchschnittswert von
) lag, welche Zugfestigkeit aus den Zugversuchen an Stäben ohne vorherige Belastungsgeschichte ermittelt wurde (siehe den Durchschnittswert von ![]() in Tabelle 3). Die Anfangsspannung
in Tabelle 3). Die Anfangsspannung ![]() variierte zwischen den Proben, da es während des Spannvorgangs nicht möglich war, die anfängliche Spannkraft (
variierte zwischen den Proben, da es während des Spannvorgangs nicht möglich war, die anfängliche Spannkraft (![]() ) genau zu kontrollieren, sondern nur zu schätzen. Dies lag an einem unkontrollierten Kraftverlust beim Loslassen des Hydraulikzylinders nach dem Anziehen der Mutter.
) genau zu kontrollieren, sondern nur zu schätzen. Dies lag an einem unkontrollierten Kraftverlust beim Loslassen des Hydraulikzylinders nach dem Anziehen der Mutter.
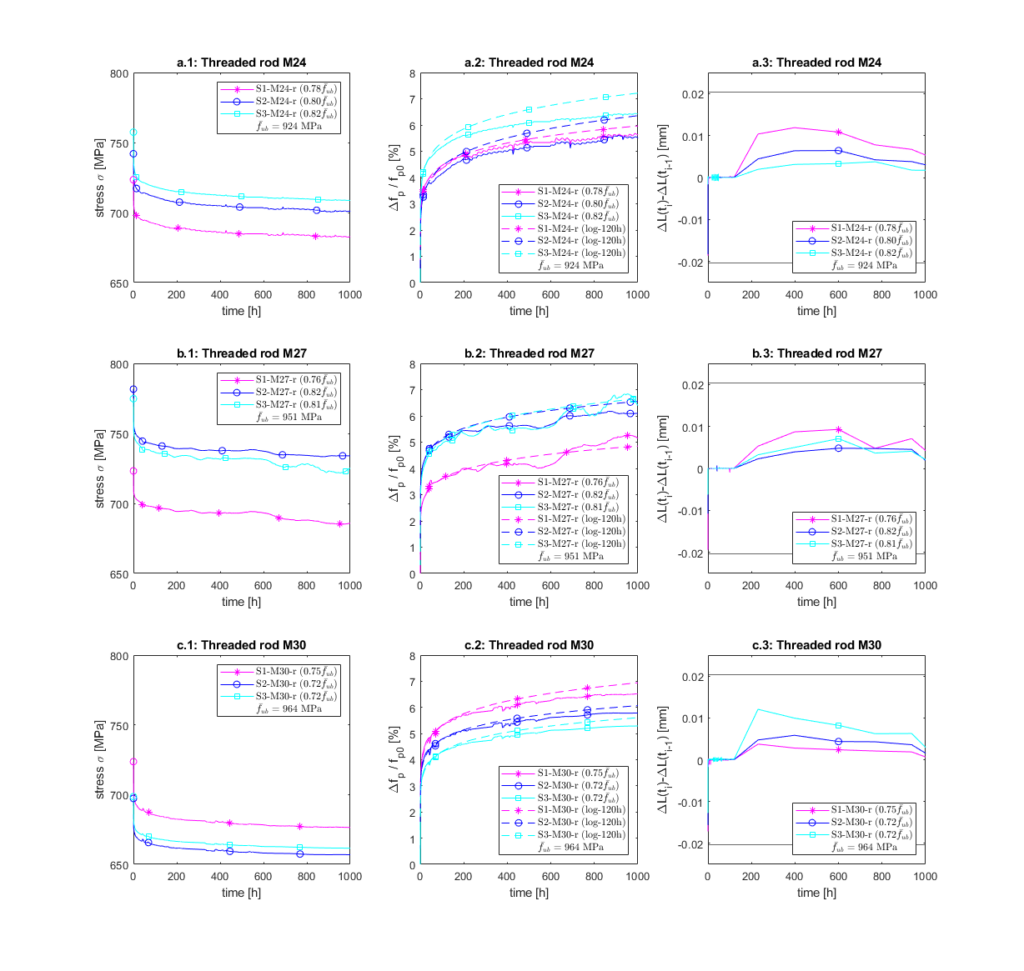
Abbildung 2 zeigt die experimentellen Spannungen, die Relaxation und die zeitliche Veränderung der Verformung für die Duplex-Gewindestangen M24, M27 und M30. Die (als positiv betrachtete) Relaxation — Spannungsverluste (![]() /
/ ![]() ) — wird als die Veränderung der Spannung im Verhältnis zur anfänglichen Spannung ausgedrückt. In den Diagrammen a.2 (M24), b.2 (M27) und c.2 (M30) in Abbildung 2 ist sie durch durchgezogene Linien dargestellt.
) — wird als die Veränderung der Spannung im Verhältnis zur anfänglichen Spannung ausgedrückt. In den Diagrammen a.2 (M24), b.2 (M27) und c.2 (M30) in Abbildung 2 ist sie durch durchgezogene Linien dargestellt.
Die Verformungsänderung, ![]() , dargestellt in Abbildung 2 (a.3, b.3 und c.3), wird überwacht, um sicherzustellen, dass die aufgezwungene Verformung innerhalb der in [3] festgelegten Grenzen konstant bleibt: “Die Veränderung von
, dargestellt in Abbildung 2 (a.3, b.3 und c.3), wird überwacht, um sicherzustellen, dass die aufgezwungene Verformung innerhalb der in [3] festgelegten Grenzen konstant bleibt: “Die Veränderung von ![]() darf zwischen zwei aufeinander folgenden Kraftmessungen 5 × 10−5
darf zwischen zwei aufeinander folgenden Kraftmessungen 5 × 10−5 ![]() nicht überschreiten “. Bei den Relaxationsversuchen beträgt die Referenzlänge
nicht überschreiten “. Bei den Relaxationsversuchen beträgt die Referenzlänge ![]() = 405 mm; die maximal zulässige Abweichung zwischen zwei aufeinanderfolgenden Kraftmessungen beträgt somit ± 0.0203 mm. Die Referenzkraftmessungen sind in Tabelle 2 der Quelle [3] angegeben. Die grössten Abweichungen (innerhalb der zulässigen Werte) treten unmittelbar in den ersten Sekunden auf und sind auf ein leichtes Abrutschen der Muttern zurückzuführen, welche die Kraft aufnehmen. Die übrigen Schwankungen liegen deutlich innerhalb der Toleranzgrenzen (± 0.0203 mm), was die ausreichende Steifigkeit der Prüfstände für die Durchführung von Relaxationsversuchen bestätigt.
= 405 mm; die maximal zulässige Abweichung zwischen zwei aufeinanderfolgenden Kraftmessungen beträgt somit ± 0.0203 mm. Die Referenzkraftmessungen sind in Tabelle 2 der Quelle [3] angegeben. Die grössten Abweichungen (innerhalb der zulässigen Werte) treten unmittelbar in den ersten Sekunden auf und sind auf ein leichtes Abrutschen der Muttern zurückzuführen, welche die Kraft aufnehmen. Die übrigen Schwankungen liegen deutlich innerhalb der Toleranzgrenzen (± 0.0203 mm), was die ausreichende Steifigkeit der Prüfstände für die Durchführung von Relaxationsversuchen bestätigt.
Tabelle 3 fasst die anfänglichen (![]() ) Spannungen sowie die Relaxation (Verlustquote der Vorspannung),
) Spannungen sowie die Relaxation (Verlustquote der Vorspannung), ![]() /
/![]() , nach 10 Minuten, 120 Stunden und 1’000 Stunden von Duplex-Gewindestangen M24, M27 und M30 gemäss Abbildung 2 zusammen. Die durchschnittliche Relaxation nach 1’000 Stunden beträgt für die drei Gewindestangengrössen (M24, M27 und M30) etwa 6%, bei anfänglichen Spannungen zwischen dem 0.70- und 0.85-fachen
, nach 10 Minuten, 120 Stunden und 1’000 Stunden von Duplex-Gewindestangen M24, M27 und M30 gemäss Abbildung 2 zusammen. Die durchschnittliche Relaxation nach 1’000 Stunden beträgt für die drei Gewindestangengrössen (M24, M27 und M30) etwa 6%, bei anfänglichen Spannungen zwischen dem 0.70- und 0.85-fachen ![]() . Die Entwicklung der Relaxation im Laufe der Zeit ähnelt einem logarithmischen Wachstum, wobei die grösste Veränderung innerhalb der ersten 120 Stunden auftritt. Etwa 30% und 80% der Relaxation nach 1’000 Stunden treten innerhalb der ersten 10 Minuten bzw. 120 Stunden auf.
. Die Entwicklung der Relaxation im Laufe der Zeit ähnelt einem logarithmischen Wachstum, wobei die grösste Veränderung innerhalb der ersten 120 Stunden auftritt. Etwa 30% und 80% der Relaxation nach 1’000 Stunden treten innerhalb der ersten 10 Minuten bzw. 120 Stunden auf.
| Probe | ||||||||
| [MPa] | [MPa] | [MPa] | [MPa] | [-] | [%] | [%] | [%] | |
| S1-M24-r | 911 | 716 | 797 | 725 | 0.78 | 1.9 | 4.5 | 5.6 |
| S2-M24-r | 911 | 738 | 791 | 747 | 0.80 | 1.4 | 4.3 | 5.5 |
| S3-M24-r | 950 | 731 | 809 | 757 | 0.82 | 2.3 | 5.3 | 6.4 |
| Avg. M24 | 924 | 728 | 799 | 743 | 0.80 | 1.9 | 4.7 | 5.8 |
| S1-M27-r | 941 | 713 | 809 | 723 | 0.76 | 1.6 | 3.7 | 5.2 |
| S2-M27-r | 970 | 720 | – | 782 | 0.82 | 2.6 | 5.2 | 6.1 |
| S3-M27-r | 942 | 709 | 855 | 775 | 0.81 | 2.3 | 5.0 | 6.4 |
| Avg. M27 | 951 | 714 | 832 | 760 | 0.80 | 2.1 | 4.6 | 5.9 |
| S1-M30-r | 996 | 783 | – | 724 | 0.75 | 1.9 | 5.4 | 6.5 |
| S2-M30-r | 938 | 777 | 855 | 697 | 0.72 | 1.8 | 4.9 | 5.8 |
| S3-M30-r | 957 | 794 | 830 | 699 | 0.72 | 1.5 | 4.4 | 5.3 |
| Avg. M30 | 964 | 785 | 842 | 706 | 0.73 | 1.7 | 4.9 | 5.9 |
| (1) Nach den direkten Zugversuchen, die an Stäben ohne vorherige Belastungsgeschichte durchgeführt wurden (2) Nach den direkten Zugversuchen, die nach den Relaxationsversuchen gemacht wurden | ||||||||
Relaxation nach 120 Stunden und theoretische Schätzungen nach 1’000 Stunden
Als Alternative zu den 1’000-Stunden-Relaxationsversuchen sieht die ISO 15630-3 [3] vor, die Versuche für einen reduzierten Zeitraum von mindestens 120 Stunden durchzuführen. Dabei kann die Relaxation nach 1’000 Stunden aus der folgenden semiempirischen Gleichung extrapoliert werden:
(2) ![]()
Dabei ist ![]() /
/![]() die Relaxation, allgemein in Prozent ausgedrückt;
die Relaxation, allgemein in Prozent ausgedrückt; ![]() ist die Zeit, ausgedrückt in Stunden, und
ist die Zeit, ausgedrückt in Stunden, und ![]() und
und ![]() sind Koeffizienten. Die Koeffizienten
sind Koeffizienten. Die Koeffizienten ![]() und
und ![]() werden durch logarithmische Regression auf der Grundlage der Versuchsergebnisse der ersten 120 Stunden ermittelt. Abbildung 2 (a2, b2 und c2) zeigt die aus der semiempirischen Gl. (2) erhaltene Relaxation, log-120h (gepunktete Linien). Es kann festgestellt werden, dass die log-120h-Kurven bis zu etwa 200 Stunden gut mit den experimentellen Kurven übereinstimmen, während sie die Relaxation nach 1’000 Stunden überbewerten.
werden durch logarithmische Regression auf der Grundlage der Versuchsergebnisse der ersten 120 Stunden ermittelt. Abbildung 2 (a2, b2 und c2) zeigt die aus der semiempirischen Gl. (2) erhaltene Relaxation, log-120h (gepunktete Linien). Es kann festgestellt werden, dass die log-120h-Kurven bis zu etwa 200 Stunden gut mit den experimentellen Kurven übereinstimmen, während sie die Relaxation nach 1’000 Stunden überbewerten.
Die aus der semiempirischen Gl. (2) abgeleiteten und mit experimentell bestimmten Daten verglichenen Relaxationswerte nach 1’000 Stunden sind in Tabelle 4 aufgeführt. Bemerkenswert ist, dass die durch Gl. (2) vorhergesagte Relaxation nach 1’000 Stunden tendenziell etwas höher ausfällt und Abweichungen von 11.3%, 1.9% bzw. 5.8% (Durchschnittswerte) für die Stäbe M24, M27 und M30 aufweist. Diese Abweichungen liegen innerhalb akzeptabler Grenzen und sind auf der sicheren Seite, wenn sie bei der Auslegung von Vorspannungen in Bauwerken berücksichtigt werden.
| Probe | |||
| exp. | Gl. (2) | ||
| [%] | [%] | [%] | |
| S1-M24-r | 5.61 | 5.96 | 6.2 |
| S2-M24-r | 5.51 | 6.36 | 15.4 |
| S3-M24-r | 6.42 | 7.21 | 12.3 |
| x̄r | 5.85 | 6.51 | 11.3 |
| S1-M27-r | 5.15 | 4.85 | -5.8 |
| S2-M27-r | 6.10 | 6.55 | 7.4 |
| S3-M27-r | 6.39 | 6.65 | 4.1 |
| x̄r | 5.88 | 6.02 | 1.9 |
| S1-M30-r | 6.52 | 6.94 | 6.4 |
| S2-M30-r | 5.79 | 6.07 | 4.8 |
| S3-M30-r | 5.29 | 5.61 | 6.0 |
| x̄r | 5.87 | 6.21 | 5.8 |
Diskussion und Empfehlungen
Die Relaxationsversuche an Duplex-Gewindestangen führten zu durchschnittlichen Verlusten von etwa 6% nach 1’000 Stunden, wobei der Verlauf im Laufe der Zeit einem logarithmischen Wachstum ähnelt. Die grösste Veränderung tritt innerhalb der ersten 120 Stunden auf. Ungefähr 30% bzw. 80% der Relaxation nach 1’000 Stunden findet innerhalb der ersten 10 Minuten bzw. 120 Stunden statt Allerdings wurde auf Grundlage von Vergleichen zum Zeitpunkt der 10. Minute während der direkten Zugrelaxationsversuche beobachtet, dass Gewindestangen, die zuvor Belastungs- und Entlastungszyklen ausgesetzt waren (in dieser Versuchskampagne aufgrund der Relaxationsversuche selbst), eine um 50% geringere Relaxation aufwiesen als Stangen ohne vorherige Belastungsgeschichte. Dieser Effekt führte zu einer Reduktion der Relaxation um 15 % bei vorgespannten Duplex-Gewindestangen nach 1’000 Stunden. Es ist wichtig zu beachten, dass die Ergebnisse der direkten Zugversuche in diesem Beitrag nicht dargestellt werden.
Um eine experimentelle Versuchsreihe mit möglichst hohen Anfangsspannungen in den Gewindestangen durchzuführen —sodass ihr Verhalten potenziell eine Anwendung in den Nachspannen von Tragwerken abbilden könnte—, wurden diese Spannungen maximiert. Infolgedessen wurden die Stangen Anfangsspannungen ausgesetzt, die über der in den technischen Produktspezifikationen angegebenen Mindeststreckgrenze lagen [4] (![]() > 700 MPa; siehe Tabelle 3). Darüber hinaus erhöhte der durch die Relaxationsversuche verursachte Be- und Entlastungsprozess die Streckgrenze der Gewindestangen im Vergleich zu den direkten Zugversuchen an Stäben ohne vorherige Belastungsgeschichte um mindestens 7% (siehe Tabelle 3), d. h. um mindestens 13% im Vergleich zu der in [4] angegebenen Mindeststreckgrenze. Man beachte, dass die Spannungs-Dehnungs-Kurve nichtrostender Stähle auch im Gebrauchsbereich ein nichtlineares Verhalten aufweist, was zu einem niedrigeren Elastizitätsmodul nach genormten Abschätzungskriterien führt.
> 700 MPa; siehe Tabelle 3). Darüber hinaus erhöhte der durch die Relaxationsversuche verursachte Be- und Entlastungsprozess die Streckgrenze der Gewindestangen im Vergleich zu den direkten Zugversuchen an Stäben ohne vorherige Belastungsgeschichte um mindestens 7% (siehe Tabelle 3), d. h. um mindestens 13% im Vergleich zu der in [4] angegebenen Mindeststreckgrenze. Man beachte, dass die Spannungs-Dehnungs-Kurve nichtrostender Stähle auch im Gebrauchsbereich ein nichtlineares Verhalten aufweist, was zu einem niedrigeren Elastizitätsmodul nach genormten Abschätzungskriterien führt.
Zudem betrugen die durchschnittlichen Vorspannspannungen das 0.78-fache der durchschnittlichen Zugfestigkeit aller Serien (![]() ), d.h.
), d.h. ![]() = 736 MPa. Diese Werte sind höher als die Bemessungszugfestigkeit fsd = 576 MPa (Gl. (1)), unter Berücksichtigung von
= 736 MPa. Diese Werte sind höher als die Bemessungszugfestigkeit fsd = 576 MPa (Gl. (1)), unter Berücksichtigung von ![]() = 800 MPa (Mindestzugfestigkeit gemäss [4]).
= 800 MPa (Mindestzugfestigkeit gemäss [4]).
Wenn die Berechnungen für das in Tabelle 1 dargestellte Beispiel erneut durchführt werden und dabei eine anfängliche Vorspannkraft von ![]() = 760 MPa (etwa das 0.80-fache der durchschnittlichen Festigkeit aller Serien,
= 760 MPa (etwa das 0.80-fache der durchschnittlichen Festigkeit aller Serien, ![]() ) und eine unendliche Relaxation von 6% berücksichtigt wird, ist feststellbar, dass die gesamten Spannkraftverluste 20% betragen. Dies liegt unter den 27% Verlusten, die in den vorläufigen Berechnungen (Tabelle 1) ermittelt wurden. Vorspannungsverluste von etwa 20% werden im Allgemeinen als akzeptabel für die Bemessung von vorgespannten Strukturen angesehen. Zu beachten ist, dass die in Gl. (1) angegebene Begrenzung der Bemessungszugfestigkeit ignoriert wurde und die in der technischen Produktdokumentation [4] definierte Mindeststreckgrenze bei dieser neuen Abschätzung überschritten wird.
) und eine unendliche Relaxation von 6% berücksichtigt wird, ist feststellbar, dass die gesamten Spannkraftverluste 20% betragen. Dies liegt unter den 27% Verlusten, die in den vorläufigen Berechnungen (Tabelle 1) ermittelt wurden. Vorspannungsverluste von etwa 20% werden im Allgemeinen als akzeptabel für die Bemessung von vorgespannten Strukturen angesehen. Zu beachten ist, dass die in Gl. (1) angegebene Begrenzung der Bemessungszugfestigkeit ignoriert wurde und die in der technischen Produktdokumentation [4] definierte Mindeststreckgrenze bei dieser neuen Abschätzung überschritten wird.
Hochfeste Duplex-Gewindestangen könnten eine mögliche Lösung für die externe Vorspannung von Bauwerken darstellen. Ihre wesentlichen Einschränkungen ergeben sich jedoch aus ihrer geringen Streckgrenze, der Bemessungszugfestigkeit nach SIA 263:2013 [2] (Gewindestangen werden als Schrauben betrachtet) und der Unsicherheit der Relaxation.
Daher werden im Folgenden einige Empfehlungen oder Massnahmen aufgeführt, um die Einschränkungen zu überwinden und die Verwendung von Duplex-Gewindestangen für externe Vorspannungen zu fördern:
- Die Gewindestangen werden vor dem Vorspannen einem Be- und Entlastungsprozess unterzogen (0.80…0.90-fache Zugfestigkeit,
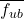 ). So bleibt das elastische Verhalten während des Vorspannens erhalten, Relaxationseffekte werden gemildert und die Spannungssteuerung kann durch elastische Verformungen genauer kontrolliert werden.
). So bleibt das elastische Verhalten während des Vorspannens erhalten, Relaxationseffekte werden gemildert und die Spannungssteuerung kann durch elastische Verformungen genauer kontrolliert werden. - Idealerweise sollten Duplex-Gewindestangen, die für das Vorspannen bestimmt sind, in der Produktionsstätte einem Vorspannprozess unterzogen werden. Darüber hinaus sollten in den technischen Unterlagen die mechanischen Eigenschaften des Produkts genauer definiert werden, einschliesslich der empfohlenen Werte für die Anfangsspannung beim Vorspannen (0.70…0.85·
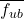 ) und der entsprechenden geschätzten Relaxation.
) und der entsprechenden geschätzten Relaxation. - Überarbeitung der Anwendbarkeit der in der SIA 263:2013 definierten Abschätzung der Bemessungszugfestigkeit für Duplex-Gewindestangen, die für Vorspannzwecke bestimmt sind.
Es ist zu beachten, dass die gegebenen Empfehlungen und Schlussfolgerungen aus einer begrenzten Versuchskampagne mit einer kleinen Anzahl von Proben abgeleitet sind. Daher sind diese Ergebnisse vorläufig, und es ist eine umfangreichere Versuchskampagne erforderlich, um einen sichereren Wert der Relaxation als Funktion des Spannungsniveaus und des Gewindestangendurchmessers sowie den Einfluss der Vorspannung auf das mechanische Verhalten des Materials zu ermitteln.
Alejandro Giraldo Soto
Referenzen
- Schweizerischer Ingenieur- und Architektenverein (SIA), SIA 263: Stahlbau. Zürich: SIA, 2013.
- Schweizerischer Ingenieur- und Architektenverein (SIA), SIA 262: Betonbau. Zürich: SIA, 2013.
- ISO, “ISO 15630-3 Steel for the reinforcement and prestressing of concrete (Test methods) Part 3: Prestressing steel,” Geneva, Switzerland, 2019.
- Leviat AG, “Nichtrostende Bewehrungen für die Bauindustrie.” Jun. 2019.
Link to English version: Thoughts on the evolution of Civil Engineering education
In den letzten Jahren wurde die Arbeitsweise der Hochschuleinrichtungen auf zweierlei Weise disruptiv beeinflusst: erstens durch die Beschränkung der physischen Anwesenheit während der Pandemie und zweitens durch die rasanten Fortschritte beim maschinellen Lernen (ML) und der künstlichen Intelligenz (KI). Die erste Störung war abrupt und erforderte eine rasche Anpassung an Online-Lehrmethoden, während die zweite sich schnell und unvorhersehbar entwickelt. Beide Entwicklungen stellen traditionelle Ansätze für das Lernen, Lehren und Bewerten in Frage. Diese Veränderungen haben mich dazu veranlasst, über meinen eigenen Bildungsweg nachzudenken, der mit einem früheren Umbruch zusammenfiel: der Internet-Revolution der 1990er und frühen 2000er Jahre. In diesem Blogpost1 möchte ich diese Erfahrungen in ihren spezifischen zeitlichen und institutionellen Kontext einordnen und sie mit meinen neueren Perspektiven an der ETH Zürich vergleichen, sowohl als Student als auch als Lehrer.
Mein Bildungsweg umfasst drei öffentliche Universitäten mit langjähriger Tradition im Bauingenieurwesen: ein Grundstudium an der Nationalen Technischen Universität Athen (NTUA) von 1994 bis 1999, ein Aufbaustudium an der University of Texas in Austin (UT) von 2001 bis 2003 und ein Doktoratsstudium an der Eidgenössischen Technischen Hochschule (ETH Zürich) seit 2020, alle mit einer Spezialisierung in Bauingenieurwesen. Obwohl diese Institutionen in ihrer akademischen Ausrichtung Gemeinsamkeiten aufweisen, unterscheiden sie sich über ihre geografische Lage hinaus in verschiedener Hinsicht erheblich. In den folgenden Abschnitten biete ich eine vergleichende Darstellung und eine kritische Reflexion über die unterschiedlichen Ausbildungsansätze der drei Hochschulen.
Grösse, Budget und Finanzierungsquellen, Studiengebühren
Ein wichtiger Unterschied zwischen den drei Universitäten liegt in ihrem akademischen Spektrum: Während sich NTUA und ETH hauptsächlich auf MINT-Disziplinen (Mathematik, Ingenieurwesen, Naturwissenschaften, und Technik) konzentrieren, bietet die UT Abschlüsse in fast allen akademischen Bereichen an. Dieses breitere Spektrum spiegelt sich in der Grösse der Institution wider – die Studierendenzahl an der UT ist etwa doppelt so hoch wie an der NTUA und der ETH – und beeinflusst auch die Struktur des Lehrplans, wie später noch erläutert wird.
Hinsichtlich des Budgets und der Finanzierung fallen zwei wesentliche Unterschiede auf. Erstens sind die Jahresbudgets von UT und ETH etwa eine Grössenordnung höher als das der NTUA. Zweitens: Obwohl alle drei Institutionen öffentlich finanziert werden, unterscheiden sich ihre Finanzierungsmodelle: An der NTUA und der ETH stammen rund zwei Drittel des Budgets aus staatlichen Mitteln, während an der UT nur etwa ein Zehntel staatlich unterstützt wird. Dieser Unterschied spiegelt sich in den Studiengebühren wider. Während die NTUA keine und die ETH nur minimale Studiengebühren erhebt, sind die Studiengebühren an der UT deutlich höher – vor allem für Studierende, die nicht aus dem Staat kommen. Diese finanziellen Unterschiede beeinflussen nicht nur die Zusammensetzung der Studentenschaft, sondern bis zu einem gewissen Grad auch die Motivation und die Dringlichkeit der Studenten, ihr Studium abzuschliessen.
Vielfalt
Die Vielfalt unter den Studierenden und Dozenten an jeder Hochschule wird in erster Linie durch die Unterrichtssprache geprägt, aber auch durch das Forschungsumfeld und die Beschäftigungsmöglichkeiten, die die Hochschule und das Land bieten. Die folgenden Beobachtungen beruhen auf meinen persönlichen Erfahrungen, die ich während meiner Zeit an den jeweiligen Universitäten gemacht habe, wobei der Schwerpunkt auf den Fachbereichen Bauwesen und – in geringerem Masse – Geotechnik liegt.
An der NTUA, wo der Unterricht vollständig auf Griechisch abgehalten wurde, waren fast alle Studenten und Professoren griechischer Herkunft, mit nur wenigen Ausnahmen. Die meisten Professoren hatten ihr Grundstudium an der NTUA absolviert und eine postgraduale Ausbildung im Vereinigten Königreich, in Deutschland oder in den USA absolviert.
An der UT war das Masterprogramm mit Studierenden aus einer Vielzahl von Ländern, darunter China, Indien, Südkorea, Japan, Kenia, Chile, Costa Rica, der Türkei, der Schweiz und Griechenland, bemerkenswert vielfältig. Im Gegensatz dazu stammten die Studenten im Grundstudium überwiegend aus Texas, was auf die deutlich niedrigeren Studiengebühren im Bundesstaat zurückzuführen ist. Die meisten Fakultätsmitglieder waren in den USA geboren und hatten ihr Studium im Inland abgeschlossen – viele an der Universität von Illinois in Urbana-Champaign.
An der ETH ist Deutsch die offizielle Unterrichtssprache auf der Bachelor-Stufe, während der Master-Studiengang letztes Jahr offiziell auf Englisch umgestellt wurde – obwohl viele Kurse auf Master-Stufe bereits vor der Umstellung auf Englisch abgehalten wurden. Dementsprechend sind rund drei Viertel der Bachelor-Studierenden Schweizerinnen und Schweizer. Auf der Master-Stufe nimmt der Anteil der internationalen Studierenden zu und kehrt sich auf der Doktoratsstufe um, wo der Anteil der Schweizer Studierenden rund ein Viertel beträgt. Speziell im Bauingenieurwesen ist der Anteil der Schweizer Studierenden etwas höher als im ETH-Durchschnitt. Die Dozierenden an den Instituten für Konstruktion und Geotechnik sind mehrheitlich europäischer Herkunft, Schweizerinnen und Schweizer sind in der Minderheit. Ihr Bildungshintergrund reicht von der Schweiz über die Nachbarländer bis hin zu Griechenland, Israel und den USA.
Zusammenfassend lässt sich sagen, dass ich an der UT die vielfältigste Studentenschaft angetroffen habe, während die ETH derzeit die international vielfältigste Gruppe von Professoren beherbergt. Im Gegensatz dazu hatte die NTUA die homogenste Studenten- und Fakultätsbevölkerung.
Zulassungsverfahren
Die Zulassungsverfahren für das Grundstudium sind in den drei Ländern sehr unterschiedlich und spiegeln unterschiedliche Bildungsphilosophien und institutionelle Strukturen wider.
In Griechenland werden die Zulassungen durch landesweite Prüfungen zentral vom Bildungsministerium verwaltet. Während sich die Einzelheiten im Laufe der Zeit geändert haben, ist die Kernstruktur seit Jahrzehnten erhalten geblieben. In den letzten beiden Jahren der Sekundarstufe wählen die Schüler einen von vier akademischen Bereichen: (a) Geistes-, Rechts- und Sozialwissenschaften, (b) MINT, (c) Gesundheits- und Lebenswissenschaften oder (d) Wirtschafts- und Informationswissenschaften. Jeder Bereich ermöglicht den Zugang zu den entsprechenden Universitätsprogrammen. Für den Zugang zu den Ingenieurwissenschaften ist beispielsweise der Abschluss des MINT-Bereichs erforderlich. Nach Abschluss der Sekundarschule legen die Schüler landesweite Prüfungen in vier Fächern ab; in der MINT-Bereich sind dies Mathematik, Physik, Chemie und Sprache/Literatur (letzteres ist für alle Schienen gleich). Die Schüler reichen ausserdem eine Rangliste ihrer bevorzugten Studiengänge ein (z. B. Bauingenieurwesen an der NTUA). Das Ministerium weist dann die Plätze auf der Grundlage von Prüfungsleistungen, Präferenzen und verfügbaren Plätzen pro Studiengang zu. Die Universitäten haben nur minimalen Einfluss auf die Zulassungen, da sie lediglich Aufnahmequoten und Mindestnoten festlegen. Dieses Verfahren ist weitgehend anonymisiert und standardisiert und fördert die Fairness, indem es sich auf einheitliche nationale Prüfungen und nicht auf unterschiedliche Schulnoten stützt. Die starke Abhängigkeit von einem einzigen Prüfungstag kann jedoch prüfungsstarke Studierende begünstigen und andere benachteiligen. Ausserdem hat es einen grossen privaten Nachhilfesektor gefördert, der die angestrebte sozioökonomische Inklusivität des öffentlichen Bildungswesens möglicherweise untergräbt. Nach ihrer Zulassung unterliegen die Schüler keinen Leistungs- oder Zeitbeschränkungen, so dass sie ihr Lerntempo flexibel gestalten können und die Möglichkeit haben, neben ihrer Ausbildung zu arbeiten.
In den USA verwaltet jede Universität ihre Zulassungen unabhängig durch ein umfassendes Bewerbungsverfahren. Schüler bewerben sich in der Regel in ihrem letzten High-School-Jahr bei mehreren Einrichtungen und reichen Unterlagen wie Zeugnisse, persönliche Erklärungen und optional Testergebnisse, Empfehlungsschreiben und Aufzeichnungen über ausserschulische Aktivitäten ein. Die Bewerber geben in der Regel ein bevorzugtes Studienfach an, das den Prüfungsprozess leitet, obwohl ein späterer Wechsel des Studienfachs oft möglich ist. Dieser ganzheitliche Ansatz zielt darauf ab, die Bewerber über die Noten und Testergebnisse hinaus zu bewerten und so eine umfassendere Beurteilung zu ermöglichen. Kritiker bemängeln jedoch, dass es dem Verfahren an Transparenz mangelt und es zu Verzerrungen kommen kann. An der UT werden etwa 75 % der für Bewerber aus Texas reservierten Studienplätze automatisch mit den besten 6 % der Absolventen jeder texanischen High School besetzt, um die Vielfalt zu fördern und die regionale Demografie zu repräsentieren. Die übrigen Stellen werden nach einem ganzheitlichen Verfahren besetzt.
In der Schweiz erhalten Studierende mit einer Matura im Inland in der Regel einen direkten Zugang zum Hochschulstudium ihrer Wahl. Unabhängig von der Vorbildung gilt die Zulassung zur ETH als provisorisch und wird erst nach erfolgreichem Abschluss der Prüfungen des ersten Studienjahres bestätigt, die als wichtiger akademischer Filter dienen. Bei internationalen Bewerbern hängt die Zulassung von ihrem Herkunftsland ab und kann eine vorherige Hochschulzulassung in einem verwandten Fachbereich oder eine Aufnahmeprüfung voraussetzen.
Studiengänge
Die Studiengänge an den drei Universitäten unterscheiden sich erheblich, insbesondere in Bezug auf Format und Dauer. Diese Unterschiede können den Wechsel zwischen den Einrichtungen erschweren – insbesondere für Studierende, die ein Grund- und Aufbaustudium an verschiedenen Universitäten absolvieren möchten – und können zu Unklarheiten hinsichtlich der relativen Wertigkeit der verliehenen Abschlüsse führen.
In den 1990er Jahren absolvierte ich an der NTUA ein fünfjähriges Programm, das mit einem Diplom in Bauingenieurwesen abschloss. Das Programm bestand aus neun Semestern Kursarbeit und einem Semester für die Diplomarbeit. Nach dem sechsten Semester wählten die Studenten eine Spezialisierung – Konstruktion, Verkehrswesen oder Wasserbau -, die für die letzten drei Semester des Studiums massgeblich war. Die spezifischen Kurse, die ich in der Vertiefungsrichtung „Konstruktion“ besuchte, sind in Tabelle 1 aufgeführt.
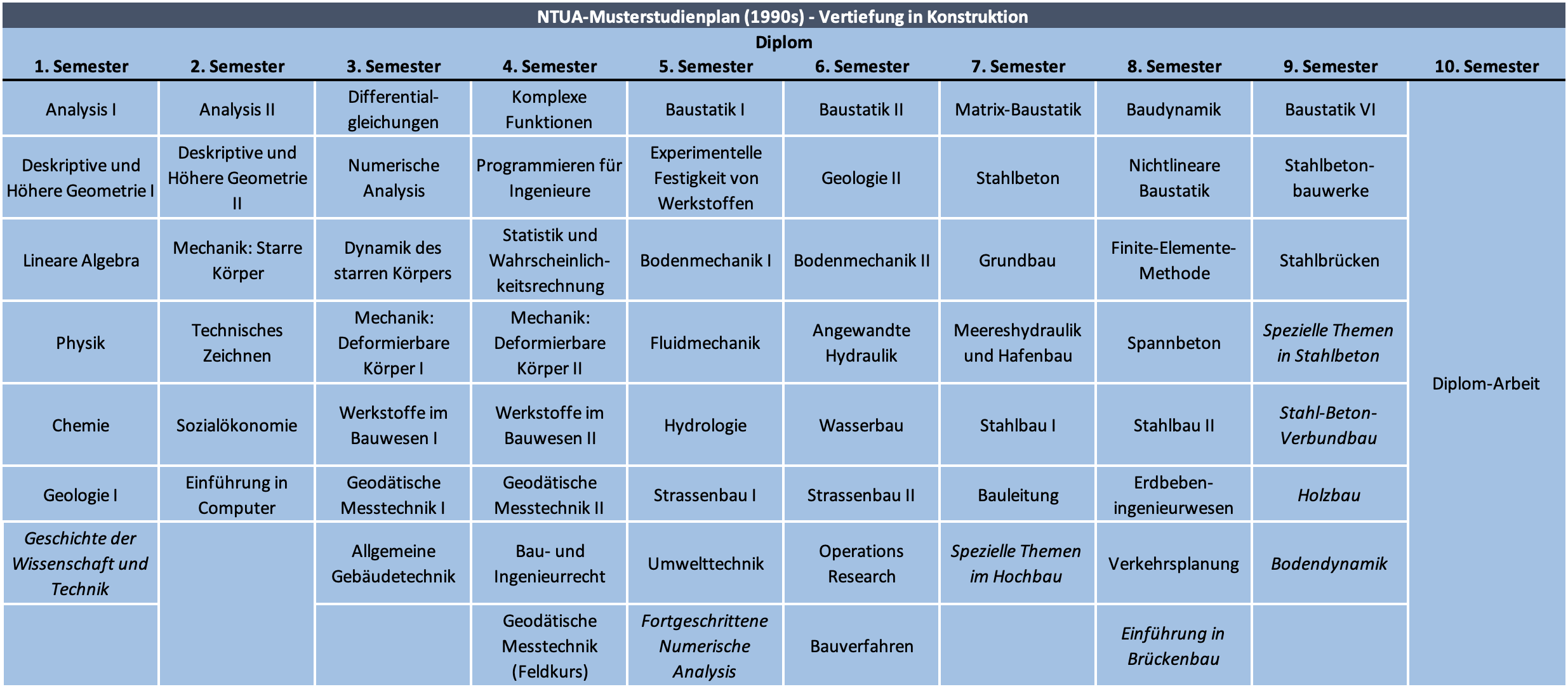
Der Studienplan war in drei Phasen gegliedert:
- Semester 1-4: Schwerpunkt auf Mathematik und Mechanik, um die Grundlage für die späteren technischen Kurse zu legen.
- Semester 5-6: Kernfächer in allen Disziplinen des Bauingenieurwesens, um den Studierenden eine breite Basis für die Wahl ihrer Spezialisierung zu bieten.
- Semester 7-9: Konzentriert sich auf die gewählte Spezialisierung, enthält jedoch auch einige interdisziplinäre Inhalte.
Mit Ausnahme des neunten Semesters waren die meisten Kurse obligatorisch. Die Voraussetzungen waren minimal, so dass die Studierenden die Kurse in flexibler Reihenfolge belegen konnten. Die Anwesenheitspflicht in den Vorlesungen war, ausser bei den Laborsitzungen, sehr locker.
Vergleicht man dies mit dem aktuellen Programm des NTUA (siehe Tabelle 2), so werden mehrere Aktualisierungen deutlich. Während die Gesamtstruktur ähnlich bleibt, sind folgende Änderungen bemerkenswert:
- Ein komprimierter Studienplan für Mathematik und Mechanik, der einen früheren Einstieg in die Themen des Bauingenieurwesens ermöglicht.
- Die Einführung eines projektbasierten Kurses im letzten Semester.
- Jährliche Laborkurse in den ersten vier Jahren zur Vertiefung der theoretischen Inhalte.
- Ein obligatorisches zweimonatiges Praktikum im letzten Semester in einer Organisation des öffentlichen oder privaten Sektors.
Mit diesen Überarbeitungen sollen offenbar bestimmte Mängel des früheren Programms behoben werden – mehr dazu im folgenden Abschnitt.
Die NTUA hat keine formale Begrenzung der Studiendauer oder der Anzahl der Versuche, einen bestimmten Kurs zu bestehen. Die Studierenden können theoretisch die meisten Lehrveranstaltungen in beliebiger Reihenfolge absolvieren, und die Leistungen werden in drei jährlichen Prüfungssitzungen bewertet:
- Wintersession: Mitte Januar bis Mitte Februar
- Sommersession: Anfang Juni bis Anfang Juli
- Septembersession: Ende August bis Ende September (für Wiederholungen oder Notenverbesserungen)
Die Absolventen erhalten den Diplomabschluss, müssen aber auch eine mündliche Prüfung vor der Technischen Kammer Griechenlands ablegen, um eine Berufszulassung als Ingenieur zu erhalten. Diese Prüfung stützt sich in der Regel auf die Diplomarbeit; vorher ist keine betreute Berufserfahrung erforderlich.
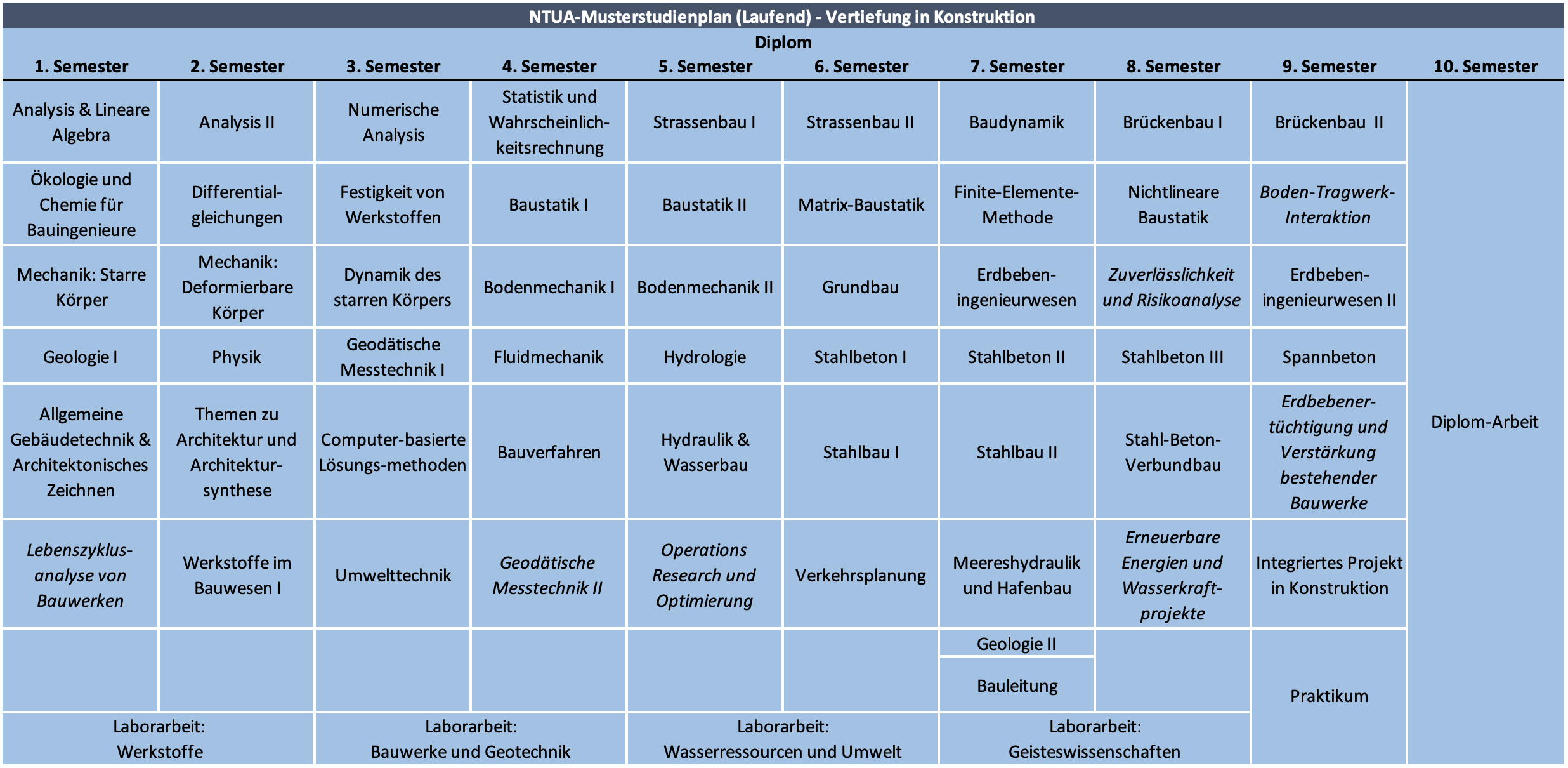
An der UT dauert das Studium, wie in den USA üblich, vier Jahre und schliesst mit dem Bachelor of Science (BSc) ab. Obwohl viele Beratungsunternehmen einen postgradualen Abschluss bevorzugen oder voraussetzen, ist es dennoch möglich, eine Karriere im Bauingenieurwesen nach dem Erwerb eines BSc-Abschlusses zu beginnen. Ein Muster für einen BSc-Studienplan ist in Tabelle 3 dargestellt. Das Programm ist in zwei Arten von Kursen gegliedert: Kernkurse, die eine breite Allgemeinbildung in Fächern wie Geschichte, Literatur und Politik vermitteln, und Hauptkurse, die auf das Bauingenieurwesen ausgerichtet sind. Die Studierenden geniessen ein gewisses Mass an Flexibilität bei der Gestaltung ihres Studiums, wobei sie häufig von einem akademischen Berater unterstützt werden. Dazu kann auch die Belegung eines Nebenfachs in einer anderen Disziplin gehören. Die Sommerpausen werden in der Regel für Praktika, Auslandsaufenthalte oder zusätzliche Lehrveranstaltungen genutzt.
Die akademischen Leistungen werden genau überwacht. Wenn die Leistungen eines Studenten unter einen bestimmten Schwellenwert fallen, kann dies zu einer akademischen Bewährung oder sogar zur Entlassung führen. In der Regel besteht Anwesenheitspflicht, und eine schlechte Anwesenheit kann zum Nichtbestehen eines Kurses führen. Ausserdem können die meisten Kurse nur einmal wiederholt werden. Die Abschlussprüfungen finden in der Woche nach dem Ende des Semesters statt. Das Herbstsemester dauert von Ende August bis Anfang Dezember, während das Frühjahrssemester Mitte Januar beginnt und Ende April endet.
Ein Vergleich zwischen den Studiengängen der NTUA und der UT zeigt einen relativen Mangel an Breite und Tiefe im Angebot der UT. Dies ist grösstenteils auf die kürzere Studiendauer und den erheblichen Zeitanteil für die Allgemeinbildung zurückzuführen. Dieser Unterschied wird jedoch durch zwei Faktoren teilweise gemildert:
- Eine postgraduale Ausbildung ist die Norm für den Einstieg in das Bauingenieurwesen.
- Die Berufszulassung ist in den USA streng geregelt.
In den USA beginnt das Zulassungsverfahren in der Regel mit der Prüfung Grundlagen des Ingenieurwesens (Fundamentals of Engineering: FE), die in der Regel im letzten Jahr des Bachelorstudiums abgelegt wird. Das Bestehen dieser Prüfung verleiht den Status: Ingenieur in Ausbildung (Engineer-in-Training: EIT). Um die Zulassung als Professioneller Ingenieur (Professional Engineer: PE) zu erlangen, muss man mehrere Jahre unter der Aufsicht eines PE arbeiten und eine zunehmende Verantwortung nachweisen. Die Anforderungen sind von Staat zu Staat unterschiedlich, umfassen aber in der Regel Referenzen und eine formale Bewerbung, um sich für die Prüfung zu qualifizieren. In einigen Staaten ist eine weitere Zulassungsstufe erforderlich, z. B. der Status Bauingenieur (Structural Engineer: SE) für Ingenieure, die komplexe Projekte wie Hochbauten oder weit gespannte Brücken leiten. Auch hierfür ist eine mehrjährige Aufsicht durch einen SE erforderlich. Ausserdem verlangen die meisten US-Bundesstaaten eine kontinuierliche Weiterbildung, um die Zulassung aufrechtzuerhalten. Trotz dieser gesetzlichen Schutzmassnahmen bin ich der festen Überzeugung, dass ein postgradualer Abschluss eine Mindestanforderung für die Ausübung des Bauingenieurwesens sein sollte. Wie ein UT-Professor bemerkte (hoffentlich etwas scherzhaft): „Es ist möglich, einen BSc-Abschluss in Bauingenieurwesen zu machen und dabei den Eindruck zu haben, dass die Welt statisch und elastisch ist.“ Ein Masterstudium an der UT ist in hohem Masse individuell gestaltbar und auf den Hintergrund und die Ziele des Studierenden zugeschnitten. Mein eigenes Masterstudium in den frühen 2000er Jahren (Tabelle 3) war flexibel, zum Teil aufgrund der umfassenden Grundlagen, die ich an der NTUA erworben hatte. Ich konnte die Kurse frei wählen, vorausgesetzt, ich belegte mindestens zwei Kurse ausserhalb des Fachgebiets „Konstruktion“. Im Gegensatz dazu würden Absolventen eines typischen amerikanischen BSc-Studiengangs ein starreres Programm mit Pflichtkursen in Mechanik, Baustatik sowie Beton- und Stahlbau absolvieren. Eine Schlüsselkomponente des Programms war die Forschungsarbeit im Master, die neben den Kursen durchgeführt wurde und in einer Masterarbeit gipfelte. Obwohl die Studierenden die Möglichkeit hatten, sich durch die Belegung zusätzlicher Kurse von der Masterarbeit zu befreien, wählten die meisten den Weg der Forschung. Viele der Forschungsprojekte wurden durch Drittmittel finanziert, die die Studiengebühren abdeckten und ein Stipendium zur Deckung der Lebenshaltungskosten boten.
Das Studienprogramm der ETH Zürich ist demjenigen der NTUA philosophisch sehr ähnlich, insbesondere in Bezug auf die starke technische Grundlage und die akademische Strenge. Ein wichtiger struktureller Unterschied ist jedoch die vollständige Umsetzung des Bologna-Prozesses an der ETH Zürich, die das Studium in einen dreijährigen Bachelor-Abschluss und einen zweijährigen Master-Abschluss gliedert. Im Gegensatz zum UT-System gilt der Bachelor-Abschluss allein nicht als berufsqualifizierend – dieser Status wird erst nach Abschluss des Masters erreicht. Dennoch entscheiden sich viele Studierende dafür, zwischen den beiden Abschlüssen eine Pause einzulegen, um Praktika zu absolvieren oder Erfahrungen in der Industrie zu sammeln – ein Weg, der sowohl üblich als auch empfohlen ist.
Der Studienplan des BSc an der ETH besteht fast ausschliesslich aus obligatorischen Kursen, die vorwiegend in deutscher Sprache unterrichtet werden. Diese vermitteln die theoretischen Grundlagen für das Masterstudium. Das Studium schliesst im sechsten Semester mit einer projektbezogenen Arbeit ab. Im Gegensatz dazu ist der Studienplan für den MSc grösstenteils wahlfrei und wird hauptsächlich in englischer Sprache unterrichtet, so dass die Studierenden ihr Studium durch die Wahl von zwei aus sechs Spezialisierungsbereichen individuell gestalten können: Konstruktion, Geotechnik, Verkehrssysteme, Wasserbau und Wasserwirtschaft, Werkstoffe und Mechanik, oder Bau- und Erhaltungsmanagement. Die abgehaltenen Kurse werden durch Projektarbeiten ergänzt und schliessen mit einer forschungsorientierten Masterarbeit im letzten Semester ab.
Die akademischen Leistungen sind streng geregelt. Im Allgemeinen dürfen die Studierenden eine nicht bestandene Prüfung nur einmal wiederholen, und es gibt keine Möglichkeit, eine bestandene Prüfung zu wiederholen, um die Note zu verbessern. Diese strengen Bewertungsregeln werden durch die Organisation bestimmter Kurse in Blöcken etwas ausgeglichen, bei denen es ausreicht, einen genügenden Notendurchschnitt für den gesamten Block zu erreichen. Dies bedeutet, dass schlechte Leistungen in einem Kurs durch gute Leistungen in einem anderen Kurs desselben Blocks ausgeglichen werden können.
Vergleicht man die drei Studienpläne, so könnte man argumentieren, dass – zumindest in der Theorie – die ETH eine Mischung aus dem umfassenden Studienplan der NTUA und der strengen akademischen Aufsicht der UT bietet.
Persönliche Überlegungen und rückblickende Bewertung
Insgesamt war meine Erfahrung an der NTUA positiv, und im Rückblick erkenne ich, dass der Studiengang mir die notwendigen Grundlagen für eine erfolgreiche Karriere im Bauingenieurwesen vermittelt hat. Nichtsdestotrotz haben einige Aspekte des Studienplans und seiner Umsetzung diese positive Erfahrung beeinträchtigt.
Nach zwei intensiven Jahren in dem Gymnasium, in denen ich mich auf die Aufnahmeprüfungen für die Universität vorbereitete – mit Schwerpunkt auf Mathematik und Physik – erwartete ich einen Perspektivenwechsel und eine Einführung in die angewandte Welt des Bauingenieurwesens. Stattdessen wurden die ersten beiden Jahre an der NTUA weitgehend in der gleichen theoretischen Richtung fortgesetzt und boten wenig bis gar keinen Zusammenhang zwischen dem Stoff und der technischen Praxis. Dieser Mangel an Integration war besonders überraschend, da alle Studenten in diesen Kursen das gleiche disziplinäre Interesse hatten, was eine massgeschneiderte, auf das Bauingenieurwesen ausgerichtete Vermittlung der Inhalte ermöglicht hätte.
Ausserdem schien der Ansatz, theoretisches Wissen vor der Einführung praktischer Anwendungen zu vermitteln, kontraintuitiv. In dem Gymnasium zum Beispiel hinkte unser mathematischer Hintergrund oft hinter dem Studienplan für Physik hinterher. Dennoch gelang es uns, die Kernkonzepte der Physik – wie Bewegung, Energie und Elektromagnetismus – zu verstehen, obwohl wir Probleme nur begrenzt rigoros lösen konnten. Sobald wir fortgeschrittenere mathematische Werkzeuge wie lineare Algebra oder Differentialrechnung lernten, wurde ihre praktische Relevanz sofort deutlich. An der Universität hingegen war diese Logik umgekehrt: Abstrakte Konzepte wurden ohne begleitende Anwendungen gelehrt. Infolgedessen war es schwierig, den Nutzen von Kursen über Informatik (2. und 4. Semester) und numerische Methoden (3. Semester) zu erkennen, da die meisten Probleme, mit denen wir bis dahin konfrontiert waren, analytisch gelöst wurden. Bis heute kann ich nicht verstehen, warum man ein ganzes Semester dem Studium komplexer Funktionen widmet. Diese „Frontloading“-Strategie hatte zwei wesentliche Konsequenzen:
- Einige Studenten verloren ganz das Interesse an ihrem Studium, während andere diese theoretischen Kurse als Pflichtübung betrachteten und sie oft auf spätere Semester verschoben;
- Am Ende des zweiten Jahres hatten die meisten Studenten den Stoff noch nicht „im Griff“, so dass die Professoren der technischen Studiengänge gezwungen waren, ihre Lehrpläne zu überarbeiten, um die wesentlichen Voraussetzungen erneut zu vermitteln. So wurden wir im Kurs Hydrologie an Statistik, im Kurs Bodenmechanik an Elastizität und den Mohrschen Kreis und in den Kursen Beton und Stahl an die Festigkeit von Werkstoffen „erinnert“. Die Trennung von Theorie und Anwendung mag zwar einige logistische Vorteile haben, aber ich glaube, dass sowohl die Zeit der Studenten als auch die der Professoren durch einen stärker integrierten und vielleicht gestrafften Studienplan effektiver genutzt werden könnte (mehr dazu im nächsten Abschnitt).
Diese Annahme wird auch durch die offiziellen Kursstatistiken gestützt, die in den einführenden Mechanikkursen häufig Bestehensquoten von weniger als 15 % ausweisen – trotz deutlich höherer Bestehensquoten (>50 %) in späteren Kursen wie Bodenmechanik oder Stahlbau, wo erstere theoretisch Voraussetzung ist.
Das Arbeitspensum und die Intensität des Studiengangs haben in den letzten drei Jahren erheblich zugenommen. Ein typisches Semester umfasste etwa 35 Stunden Vorlesungen, Kolloquien oder Laborsitzungen pro Woche. Obwohl die Anwesenheit in der Regel nicht verpflichtend war, wurde sie immer wichtiger. Hausarbeiten und Semesterprojekte, die häufig in den Weihnachts- und Osterferien angefertigt wurden, erhöhten das Arbeitspensum zusätzlich. Ein grosser Teil des Lernens fand während der einmonatigen Prüfungszeiträume statt, da es fast unmöglich war, während des Semesters in allen Kursen den Überblick zu behalten. Infolgedessen schloss nur ein kleiner Prozentsatz der Studenten das Studium rechtzeitig ab; die meisten brauchten sechs oder sieben Jahre, um den Studiengang abzuschliessen, ein Trend, der wahrscheinlich anhält.
Ein Aspekt, den ich besonders schätzte, war das Spektrum der praktischen Projekte, die wir durchführten: ein Autobahnabschnitt, ein kleines Hydrauliksystem, Wohn- und Industriegebäude aus Stahlbeton, ein Stahlhangar, Spannbeton- und Stahlfachwerkbrücken, ein Holzhaus und eine Hafenmole. Diese Projekte förderten zwar nicht die Kreativität, ermöglichten aber die praktische Anwendung von Entwurfs- und Analyseprinzipien. Insbesondere wurden alle Berechnungen manuell durchgeführt (mit Ausnahme einiger Tabellenkalkulationen), und alle Zeichnungen wurden von Hand erstellt.
Angesichts der Erdbebenanfälligkeit Griechenlands konzentrierten sich viele der Konstruktions- und Geotechnikkurse auf erdbebensicheres Design. Folglich haben wir uns eingehend mit dynamischem und unelastischem Verhalten befasst, wobei der Schwerpunkt auf duktilen Details lag. Vielleicht hat dieser seismische Kontext dazu geführt, dass ein konservativer Ansatz bei der Konzeptionierung vorherrschte. Die Studenten wurden oft auf einfache und robuste Struktursysteme verwiesen, die mit relativ einfachen Mitteln analysiert, entworfen und gebaut werden konnten. Damit sollte wahrscheinlich sichergestellt werden, dass die Absolventen zunächst vorhersehbare und sichere Entwürfe erstellen würden. Dies mag jedoch auch zu dem etwas eintönigen und wenig inspirierenden Erscheinungsbild vieler griechischer Städte beigetragen haben.
Zu den Höhepunkten meines Studiums gehörten Studienreisen ins Ausland – nach Mitteleuropa, Japan und in den Nordosten der USA – während des dritten und fünften Studienjahres. Diese Erfahrungen boten wertvolle Einblicke in verschiedene Ansätze der Ingenieurpraxis, ästhetische Werte, Baumaterialien und Umweltbedingungen.
Zwischen meinem Abschluss an der NTUA und dem Beginn meines Studiums an der UT (1999-2001) änderte sich die Art und Weise, wie auf Informationen zugegriffen wurde, mit dem Aufkommen des Internets dramatisch. Google war gerade auf den Markt gekommen (1998), die Dot-Com-Blase erreichte ihren Höhepunkt und die Web 2.0-Ära begann. An der NTUA bezog ich meine Informationen hauptsächlich von Professoren, der Universitätsbibliothek und einigen nahe gelegenen Fachbuchläden. Ich nutzte das Internet zum ersten Mal systematisch, um nach Graduiertenprogrammen in den USA zu suchen und mich dort zu bewerben. Als ich an der UT ankam, erhielten wir von einem Bibliothekar einen kurzen Kurs über die Nutzung von Online-Recherchetools – eine Erfahrung, die meine Studien- und Forschungsgewohnheiten im Vergleich zu dem eher geschützten akademischen Umfeld an der NTUA erheblich veränderte.
Viele andere Unterschiede zwischen NTUA und UT waren ebenfalls auffällig. An der NTUA war der Unterricht meist einseitig und vorlesungslastig, mit wenig Gelegenheit zum aktiven Lernen. Die Studierenden arbeiteten individuell, und das Lernen fand hauptsächlich kurz vor den Prüfungen statt, oft mit einem kurzfristigen, auswendig gelernten Schwerpunkt. Bestnoten waren fast unmöglich zu erreichen; in einigen Kursen schien sogar ein Bestehen erstrebenswert. Im Gegensatz dazu verfolgte die UT ein eher interaktives Lehrmodell. Die Vorlesungen umfassten nur 9-12 Stunden pro Woche, ergänzt durch regelmässige Lektüre und obligatorische Hausaufgaben, die dreimal so viel Arbeit ausserhalb des Unterrichts erforderten. Teamprojekte waren üblich. Da während des gesamten Semesters kontinuierlich gelernt wurde und Zwischenprüfungen Teil der Bewertung waren, waren Abschlussprüfungen für Studenten, die konsequent gearbeitet hatten, oft eine reine Formalität, bei der eine flüchtige Wiederholung des Stoffes normalerweise ausreichte, um die Höchstnote zu erreichen. Wöchentliche Seminare mit Fachleuten aus der Industrie und Ehemaligen boten ebenfalls nützliche Gelegenheiten zum Kennenlernen und Networking.
Der vielleicht bemerkenswerteste Unterschied lag in der Verwendung von Computern und Industriestandards in den Konstruktionskursen. An der NTUA wurde der Schwerpunkt auf manuelle Berechnungen gelegt, und der Zugang zu Computern war minimal. An der UT wurden die Studenten ermutigt, symbolische Mathematiksoftware zu verwenden, und hatten universellen Zugang zu Computern. Sogar im Grundstudium wurde Software für finite Elemente in die Strukturanalysekurse integriert. Während an der NTUA das grundlegende Verhalten neben den Anforderungen der Konstruktionsvorschriften gelehrt wurde, konzentrierten sich die Bachelor-Kurse an der UT auf die Anwendung der Konstruktionsvorschriften und behielten die theoretischen Grundlagen für die Master-Ebene vor. Dieser Ansatz ist teilweise durch die Erwartungen der Industrie geprägt: US-Arbeitgeber suchen Absolventen – auch auf BSc-Ebene -, die bereit sind, an Entwurfs- und Dokumentationsaufgaben unter Verwendung von Standardsoftware und Normen mitzuwirken.
An der UT hatte ich auch mit offeneren Aufgabenstellungen zu tun, bei denen die Studenten strukturelle Systeme unter vorgegebenen Bedingungen konzipieren und Alternativen ganzheitlich bewerten sollten. Meine in den USA ausgebildeten Studienkollegen zeigten Qualitäten, die hervorstachen: effektive Teamarbeit, Initiative, Präsentationsfähigkeiten und Selbstvertrauen beim Vorschlagen von Konzepten – auch wenn diese nicht immer auf einer soliden technischen Grundlage beruhten. Ich führe diese Stärken auf die Betonung von Initiative und Innovation im amerikanischen Bildungssystem, den frühen Kontakt mit der Industrie und die allgemeine unternehmerische Kultur zurück.
Die Unterrichtsphilosophie der ETH ist eng an die der NTUA angelehnt. Die Semester sind um die Vorlesungen herum strukturiert und das Lernen konzentriert sich auf die Zeit vor den Prüfungen. Die Teilnahme während des Semesters – der Besuch von Vorlesungen oder die Abgabe von Hausaufgaben – ist in der Regel freiwillig. Die ETH-Vorlesungen sind in der Regel noch weniger interaktiv als die der NTUA, und die Studierenden neigen eher zum passiven als zum aktiven Lernen. Die Umstellung auf Online-Vorlesungen auf Abruf während der Pandemie könnte die Lerngewohnheiten weiter beeinflusst haben. Innovation und kritisches Denken werden an der ETH jedoch stark gefördert. Die Studierenden können sich in praxis- und forschungsorientierten Projekten engagieren, insbesondere im Rahmen von Projekt- und Masterarbeiten oder durch Assistenzfunktionen in der Laborforschung.
Während meiner Lehrtätigkeit an der ETH, die sich in erster Linie auf den Brückenbau konzentrierte, aber auch Kollegen aus dem Departement für Architektur in Lehrveranstaltungen zum Tragwerksentwurf unterstützte, wurde schnell deutlich, dass grossen Wert auf den Entwurf von Bauwerken mit hoher ästhetischer Qualität gelegt wird – weit mehr als an der NTUA oder UT. Dies wird deutlich, wenn man die optischen Qualitäten vieler Schweizer Brücken mit den eher zweckmässigen Gegenstücken in Griechenland und den USA vergleicht. Darüber hinaus sind Effizienz- und Nachhaltigkeitskonzepte in den Vordergrund des Studienplans gerückt – eine Veränderung gegenüber den 1990er und frühen 2000er Jahren.
Ein wesentlicher Unterschied zwischen UT und ETH ist die Rolle der Doktorierenden in der Lehre. An der UT kümmerten sich vor allem Lehrassistenten um die Benotung und die Labore, während die Professoren die Masterarbeiten betreuten. An der ETH sind die Doktorierenden stärker involviert: Sie entwickeln Kursmaterial, leiten Übungen, entwerfen Prüfungen und betreuen Bachelor-, Projekt- und Masterarbeiten. Die Lehre auf der Bachelorstufe wird zusätzlich durch Masterstudierende unterstützt. Doktorierende an der ETH sammeln daher typischerweise viel mehr Lehr- und Betreuungserfahrung als jene an der UT. An der NTUA waren die Aufgaben der Doktoranden je nach betreuendem Professor sehr unterschiedlich, ähnelten aber im Allgemeinen eher dem ETH-Modell.
Ideen für die Zukunft
Mit Blick auf die Zukunft der Bauingenieurausbildung haben sich die jüngsten Diskussionen zunehmend auf die technologischen Entwicklungen im Bereich des maschinellen Lernens und der künstlichen Intelligenz (ML/KI) konzentriert und darauf, wie diese sowohl die Lehre als auch die Praxis des Ingenieurwesens beeinflussen könnten. Meiner Ansicht nach verstärken solche Fortschritte jedoch nur die Bedeutung eines soliden Fundaments an grundlegenden Konzepten, die durch einen klassischen Studienplan vermittelt werden, der in der Ingenieursmechanik und der Strukturtheorie verwurzelt ist und den Schwerpunkt auf manuelle und intuitive Berechnungsmethoden legt. Während sich die Materialwissenschaft, die Konstruktionsverfahren und die Berechnungswerkzeuge weiterentwickeln und die Art und Weise, wie wir Bauwerke analysieren, entwerfen, konstruieren und überwachen, verändern werden, bleiben die Kernprinzipien wesentlich und dienen als Grundlage für sinnvolle Innovationen.
Bei der Gestaltung künftiger Studiengänge ist es wichtig, zwischen Fächern zu unterscheiden, die sich am besten für die akademische Ausbildung eignen, und solchen, die eher für die Weiterbildung oder die Ausbildung am Arbeitsplatz geeignet sind. Kein akademischer Studiengang kann vollständig auf die breite Palette möglicher Karrierewege zugeschnitten sein, noch kann er mit jeder technologischen Entwicklung Schritt halten. Was er jedoch tun kann, ist, den Studierenden ein tiefes Verständnis der Grundlagen zu vermitteln und eine Einstellung zum lebenslangen Lernen zu kultivieren, die es ihnen ermöglicht, sich an neue Herausforderungen anzupassen und neue Methoden mit Zuversicht anzunehmen.
Was die Reihenfolge der Lehrveranstaltungen angeht, würde ich den herkömmlichen Ansatz in Frage stellen, den Studienplan in den ersten Semestern mit theoretischen Kursen zu füllen, die oft ohne Bezug zur realen Welt angeboten werden. Ich glaube, dass es sowohl machbar als auch ansprechender ist, Kurse, die keine fortgeschrittene Mathematik oder Berechnungswerkzeuge erfordern – wie einführende Mechanik und Statik sowie Themen der allgemeinen Bauplanung, Infrastrukturelemente und zugehörige Bauverfahren – bereits im ersten Jahr einzuführen. Auf diese Weise würden die Studierenden schon früh mit der Art von Problemen konfrontiert, mit denen sie im Laufe ihres Studiums konfrontiert werden, was den Kontext für die nachfolgenden, anspruchsvolleren Kurse schafft. Dieser Ansatz hat das Potenzial, das Engagement der Studierenden zu steigern und die Lernergebnisse zu verbessern.
Da die meisten von uns besser lernen, indem sie etwas tun, als zuzuhören, würde ich eine relative Verringerung der Vorlesungsstunden und eine entsprechende Erhöhung des aktiven Lernens durch zugewiesene Lektüre, Laborarbeit und obligatorische Einzel- und Gruppenaufgaben unterstützen. Gleichzeitig würde ich den Schwerpunkt weg von den anspruchsvollen Prüfungen am Ende des Semesters verlagern und mehr Gewicht auf kontinuierliches Lernen legen. Dies könnte dadurch erreicht werden, dass der Einfluss der Abschlussprüfung auf die Gesamtnote des Kurses verringert wird und mehr Gewicht auf wöchentliche Aufgaben und Semesterprojekte gelegt wird.
Abschliessend wäre ich sehr daran interessiert zu erfahren, wie meine Erfahrungen an der Universität im Vergleich zu denen anderer Universitäten in der ganzen Welt und über verschiedene Zeiträume hinweg aussehen, und mich darüber auszutauschen, wie sich die Bauingenieurausbildung so weiterentwickeln könnte, so dass sie unseren Gemeinschaften besser dient.
“Bildung ist das, was übrig bleibt, wenn man vergessen hat, was man in der Schule gelernt hat.”
Albert Einstein
“Bildung bedeutet nicht das Erlernen von Fakten, sondern die Schulung des Denkens.”
Haftungsausschluss
Ohne Verlust der Allgemeingültigkeit wurden die Informationen und Statistiken zu den oben genannten Hochschulprogrammen vereinfacht und/oder gerundet, um einen Vergleich und eine bessere Lesbarkeit zu ermöglichen. Sie spiegeln möglicherweise nicht die aktuellsten Daten wider, die zum Zeitpunkt der Veröffentlichung dieses Blogbeitrags verfügbar waren.
George Klonaris
- The cover image was created on 16.10.2024 with DALL-E. ↩︎
Link to English version: A new approach for a shell element of the finite element analysis
In diesem Blogpost werde ich mich darauf konzentrieren, die Entwicklung eines neuartigen sogenannten „hybriden Machine-Learning-Finite-Elemente-Analyse“-Ansatzes (hybride ML-FEA) für Schalenelemente zu erläutern. Insbesondere werde ich dabei den Fokus darauf legen, welche Daten zur Erstellung dieses Ansatzes verwendet wurden. In meinem letzten Blogpost habe ich bereits die Motivation für die Verwendung von Machine Learning in der Finite-Elemente-Analyse für Stahlbetonkonstruktionen geschildert und ein einfaches Beispiel für ein Surrogate Model («Ersatz-Modell») eines Stahlbetonbalkens gezeigt. Kurz zusammengefasst: Um die iterative Bestimmung der Krümmung aufgrund des Moments in einem potentiell gerissenen Querschnitt eines Stahlbetonträgers zu umgehen, wurde ein neuronales Netzwerk trainiert, das diese Aufgabe ersetzen kann.
Häufig werden jedoch Stahlbetonplatten und -schalen (und nicht Stahlbetonbalken) als Bestandteile in grossen Infrastrukturbauten verwendet. Abbildung 1 zeigt drei typische Beispiele von solchen Schalenelementen in der Fahrbahnplatte oder im Steg eines Brückenträgers ((a), Nr. 1 und 3) oder in einer standartmässigen Deckenplatte ((b), Nr. 2). Es ist deshalb wichtig, die Anwendbarkeit von Machine Learning in einer schalenbasierten FEA zu untersuchen, sodass ein zweckmässiger hybrider ML-FEA Ansatz für Stahlbetonbauten erstellt werden kann, welcher als Ersatz (oder Umgehung) der standardmässigen FEA dienen kann.
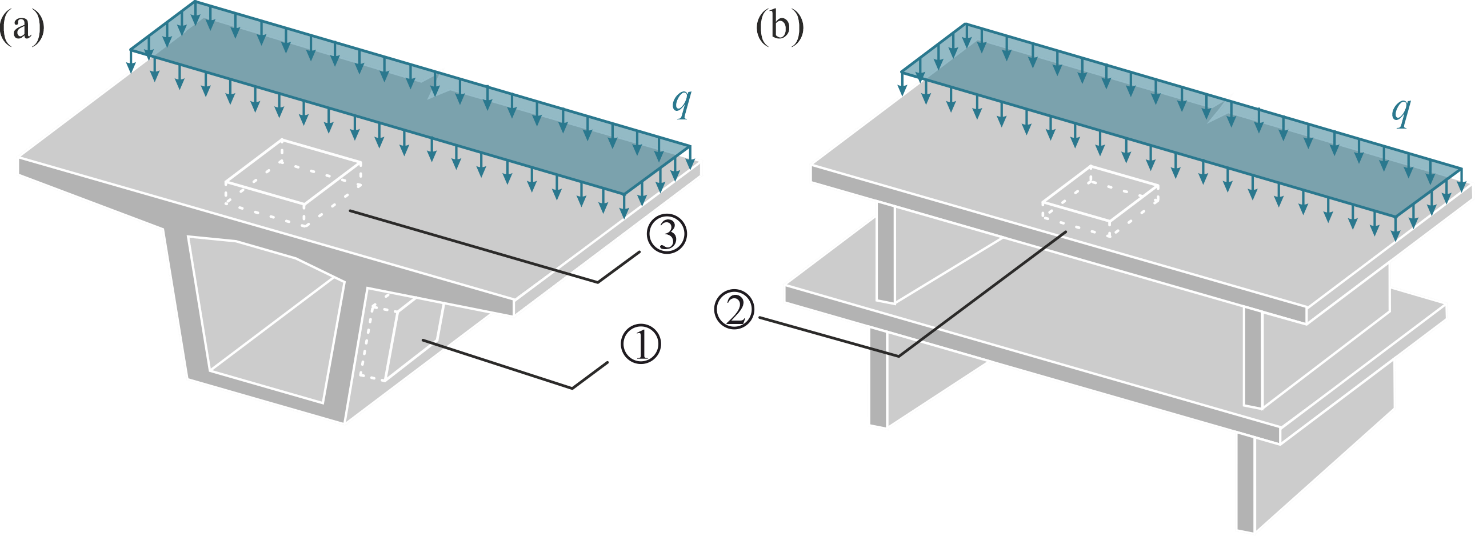
Im Vergleich zu anderen Machine-Learning basierten Surrogate Models, soll sich dieser Ansatz insbesondere durch das Niveau in der FEA auf dem er ansetzt hervorheben: Andere Methoden (z.B. Kuhn et al., siehe separater Blogpost) ersetzen die gesamte FEA oder versuchen durch den Ersatz von Spannungs(![]() )-Dehnungs(
)-Dehnungs(![]() )-Beziehungen auf einem Materialpunkt (z.B. Li et al., Neural Metamaterial Models) neue Materialmodelle zu entwickeln. Der hier vorgestellte hybride ML-FEA Ansatz soll jedoch für das finite Element Niveau erstellt werden können, das heisst für ein Schalenelement gültig sein.
)-Beziehungen auf einem Materialpunkt (z.B. Li et al., Neural Metamaterial Models) neue Materialmodelle zu entwickeln. Der hier vorgestellte hybride ML-FEA Ansatz soll jedoch für das finite Element Niveau erstellt werden können, das heisst für ein Schalenelement gültig sein.
Dies bedeutet, dass das ML Modell die Beziehung zwischen generalisierten Spannungen (![]() oder auch «resultierenden Schnittkräften») und generalisierten Dehnungen (
oder auch «resultierenden Schnittkräften») und generalisierten Dehnungen (![]() ) ersetzen soll. Beide bestehen aus acht Variablen wie sie für ein geschichtetes Schalenelement aus Stahlbeton verwendet werden (Abbildung 2 und Gleichung 1): Drei Membrankraft- resp. Membrandehnungskomponenten (
) ersetzen soll. Beide bestehen aus acht Variablen wie sie für ein geschichtetes Schalenelement aus Stahlbeton verwendet werden (Abbildung 2 und Gleichung 1): Drei Membrankraft- resp. Membrandehnungskomponenten (![]() resp.
resp. ![]() ), drei Momenten- resp. Krümmungskomponenten (
), drei Momenten- resp. Krümmungskomponenten (![]() resp.
resp. ![]() ) und zwei Querkraft- resp. Schubdehnungskomponenten: (
) und zwei Querkraft- resp. Schubdehnungskomponenten: (![]() resp.
resp. ![]() ). In Gleichung 1 entspricht
). In Gleichung 1 entspricht ![]() der generalisierten Steifigkeitsmatrix, welche den Bezug zwischen den generalisierten Dehnungen und den generalisierten Spannungen darstellt.
der generalisierten Steifigkeitsmatrix, welche den Bezug zwischen den generalisierten Dehnungen und den generalisierten Spannungen darstellt.

![Rendered by QuickLaTeX.com \[\left\{\begin{matrix} n_x, n_y, n_{xy} \\ m_x, m_y, m_{xy} \\ v_{xz}, v_{yz}\end{matrix} \right\} = \left[\mathbf{D}\right]\left\{ \begin{matrix} \varepsilon_x, \varepsilon_y, \varepsilon_{xy} \\ \chi_x, \chi_y, \chi_{xy} \\ \gamma_{xz}, \gamma_{yz}\end{matrix}\right\}\]](https://concrete.ethz.ch/wp-content/ql-cache/quicklatex.com-d5d52354e3fa2da1d0d41ff7897df52f_l3.png)
Gleichung 1: Beziehung zwischen generalisierten Spannungen und Dehnungen.
In einem ersten Beispiel der Untersuchung eines hybriden ML-FEA Ansatzes für Schalen, wird ein geschichtetes, linear-elastisches Schalenelement, basierend auf der Reissner-Mindlin Schalentheorie analysiert (Abbildung 2, Gleichung 1). Im Vergleich zu typischen Kirchhoff’schen Schalenelemente beinhalten Reissner-Mindlin-Elemente also auch Schubkomponenten und werden für dicke Schalenelemente verwendet (Gleichung 1). Aufgrund der Schichtung des Schalenelements können die individuellen Schichten, welche jeweils im ebenen Spannungszustand modelliert werden, separat analysiert werden. Während der klassischen FEA werden also zuerst die Dehnungs- und danach die Spannungszustände in jeder Schicht des Elements evaluiert. Danach werden die Spannungen über die Höhe des Elements zu den generalisierten Spannungen aufintegriert. Die lineare Elastizität vereinfacht das Problem für diesen ersten Schritt der Untersuchung und resultiert in einer geschlossenen Form für die Matrix ![]() (d.h.
(d.h. ![]() kann analytisch berechnet werden). In einem komplexeren Materialmodell, wie zum Beispiel für nichtlinearen Stahlbeton, wäre diese Matrix nicht in geschlossener Form verfügbar und müsste iterativ – je nach Dehnungszustand und entsprechendem Materialmodell – bestimmt werden (z.B. Materialmodelle, welche im gerissenen Scheibenmodell Usermat angewendet werden).
kann analytisch berechnet werden). In einem komplexeren Materialmodell, wie zum Beispiel für nichtlinearen Stahlbeton, wäre diese Matrix nicht in geschlossener Form verfügbar und müsste iterativ – je nach Dehnungszustand und entsprechendem Materialmodell – bestimmt werden (z.B. Materialmodelle, welche im gerissenen Scheibenmodell Usermat angewendet werden).
An dieser Stelle ist es wichtig zu erwähnen, dass die angenommene lineare Elastizität das Problem so fest vereinfacht, dass ein Machine Learning weder die Geschwindigkeit noch die Genauigkeit der FEA verbessern kann. Der Grund, warum dennoch ein hybrider ML-FEA Ansatz implementiert wird, liegt nur darin, die Machbarkeit eines solchen Ansatzes in einem Fall zu testen, in dem die standartmässige FEA-Lösung einfach verfügbar ist aufgrund der analytischen Lösung. In Zukunft wird das Ziel sein, diesen Ansatz auf geschichtete Scheibenelemente mit komplexeren Materialmodellen auszuweiten, wie zum Beispiel Elemente, die für nichtlineare Analysen von Stahlbeton verwendet werden.
Um das ML Modell zu erstellen, braucht es zwei Hauptkomponenten: Daten und eine passende ML Architektur. In diese Blogpost möchte ich mich auf die Datenakquisition fokussieren. In diesem ersten Schritt der Untersuchung werden die Daten aus der standartmässigen FEA generiert, es handelt sich also um sogenannte «synthetische Daten». Es dauert eine Weile bis alle benötigten Daten so simuliert werden können. Sobald jedoch der Datensatz erstellt und das ML Modell trainiert ist, dauert eine Anfrage des hybriden ML-FEA Ansatzes nicht länger als eine Berechnung mit der standartmässigen FEA. Es gibt zwei Arten, wie die Daten mittels FEA simuliert werden können: Globales und lokales Sampling (Abbildung 3). In der globalen Methode werden zuerst unterschiedliche Plattencharakteristika und Randbedingungen gewählt, die mit einem Latin Hypercube Sampler (siehe auch Wikipedia) gesampelt werden. Danach werden die generalisierten Spannungen mit einer normalen FEA ermittelt. Im Gegensatz dazu werden beim lokalen Sampling direkt die generalisierten Dehnungen mit dem Latin Hypercube Sampler ermittelt. Diese müssen dann nur durch das Materialmodell geschickt werden um die generalisierten Spannungen zu bestimmen und so den gewünschten Datensatz zu erstellen. Der endgültige Datensatz besteht dann aus n Reihen von ![]() ,
, ![]() ,
, ![]() und
und ![]() . Obwohl diese beiden Methoden auf den ersten Blick erscheinen, als ob sie dieselben Datensätze generieren würden, beeinflusst die Sampling-Methode die Trainierbarkeit der ML Modelle massgeblich: Wie in Abbildung 3 dargestellt führt der Datensatz, der aufgrund von lokalem Sampling erstellt wurde, zu viel gleichmässiger verteilten Daten und damit zu einem viel besseren Training für ein ML Modell. Es zeigt also wieder einmal, dass jedes ML Modell nur so gut ist wie die ihm zugrunde gelegten Daten.
. Obwohl diese beiden Methoden auf den ersten Blick erscheinen, als ob sie dieselben Datensätze generieren würden, beeinflusst die Sampling-Methode die Trainierbarkeit der ML Modelle massgeblich: Wie in Abbildung 3 dargestellt führt der Datensatz, der aufgrund von lokalem Sampling erstellt wurde, zu viel gleichmässiger verteilten Daten und damit zu einem viel besseren Training für ein ML Modell. Es zeigt also wieder einmal, dass jedes ML Modell nur so gut ist wie die ihm zugrunde gelegten Daten.
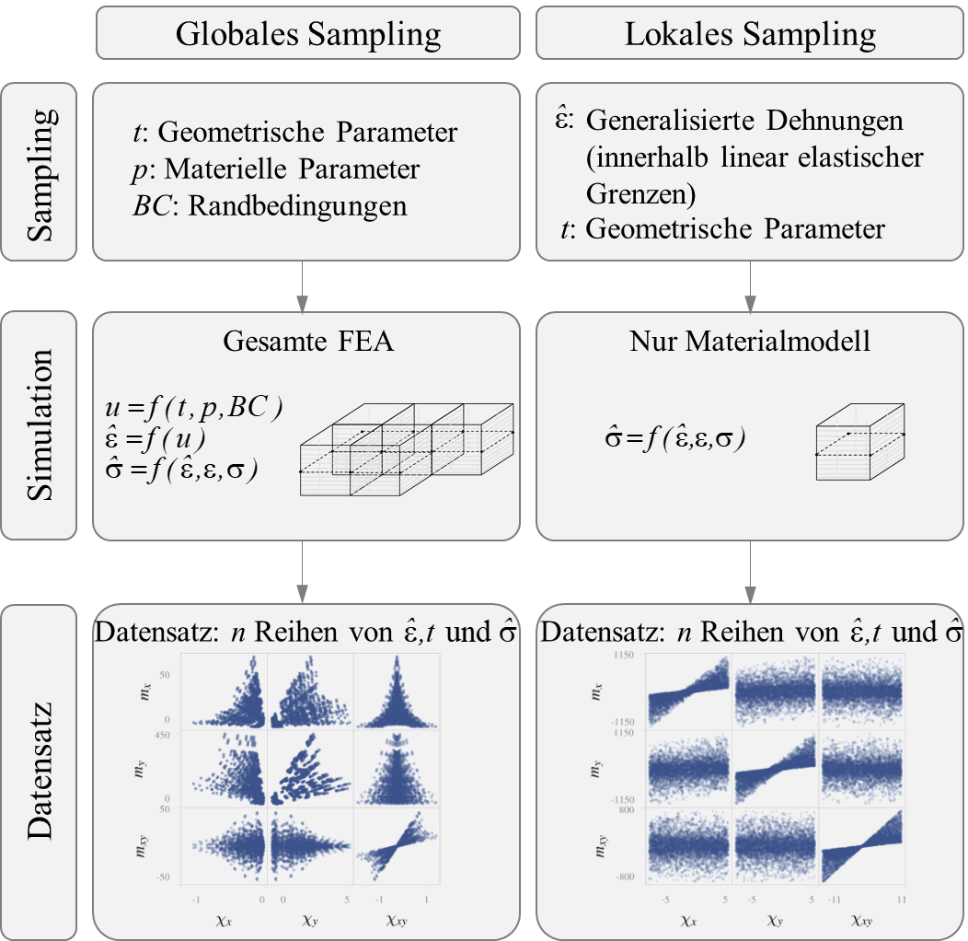
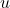 : Verschiebungen;
: Verschiebungen; 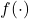 : eine Funktion).
: eine Funktion).Vielleicht fragen Sie sich nun, warum man nicht experimentelle Daten für diese Untersuchung verwendet, sondern sich die Mühe des Samplings vom linear-elastischen Materialmodell gemacht hat. Es gibt dafür zwei Gründe: Erstens handelt es sich beim betrachteten Ansatz um ein Einführungsbeispiel, das nur für linear-elastische Bedingungen verwendet werden kann, für welche die Daten aus Experimenten schwierig zu extrahieren wären und dann doch nicht das ganze Materialverhalten abbilden würden, d.h. nur den ungerissenen Teil. Zweitens sind experimentelle Daten nur spärlich verfügbar: Als nächsten Teil des Projekts, werden zurzeit experimentelle Daten von Schalenelementtests (z.B. von Experimenten am LUSET) gesammelt, um einen Datensatz für die nichtlineare Analyse von Stahlbeton zu erstellen. Zudem besteht die Möglichkeit, dass diese Daten nicht einer so schönen Verteilung folgen, wie sie für ein gutes ML Training benötigt würden.
Nach dem Sampling der Daten des linear-elastischen Materialmodells wurden verschiedene physik-basierte ML Modelle getestet, um die mechanische Beziehung ![]() in der ML Architektur einzubetten. Ein Training mit einem Deep Operator Network führte zu den besten Vorhersagen für die generalisierten Spannungen und wurde deshalb für den linear-elastischen, hybriden ML-FEA Ansatz verwendet. Detailliertere Informationen zur gewählten ML Architektur finden Sie im Paper [1]. Das Deep Operator Network wurde dann in der FEA verwendet, wobei Abbildung 4 eine Beispielberechnung von einer Deckenplatte zeigt, welche durch Biegung in eine Richtung beansprucht ist (Beispiel 2, Abbildung 1). Diese Beispielrechnung besteht aus 100 finiten Schalenelementen (10×10). Abbildung 4 zeigt nun, dass die standartmässige FEA (a) und der hybride ML-FEA Ansatz (b), in dem jedes Schalenelement mit dem ML Modell ersetzt wurde, sehr ähnliche Resultate ergeben, was weiter durch die Fehlerberechnung (c) eines normalisierten Wurzelquadratfehlers («normalised root squared error», nRSE) hervorgehoben wird. So konnte man die Machbarkeit des hybriden ML-FEA Ansatzes im vereinfachten linear-elastischen Beispiel überprüfen.
in der ML Architektur einzubetten. Ein Training mit einem Deep Operator Network führte zu den besten Vorhersagen für die generalisierten Spannungen und wurde deshalb für den linear-elastischen, hybriden ML-FEA Ansatz verwendet. Detailliertere Informationen zur gewählten ML Architektur finden Sie im Paper [1]. Das Deep Operator Network wurde dann in der FEA verwendet, wobei Abbildung 4 eine Beispielberechnung von einer Deckenplatte zeigt, welche durch Biegung in eine Richtung beansprucht ist (Beispiel 2, Abbildung 1). Diese Beispielrechnung besteht aus 100 finiten Schalenelementen (10×10). Abbildung 4 zeigt nun, dass die standartmässige FEA (a) und der hybride ML-FEA Ansatz (b), in dem jedes Schalenelement mit dem ML Modell ersetzt wurde, sehr ähnliche Resultate ergeben, was weiter durch die Fehlerberechnung (c) eines normalisierten Wurzelquadratfehlers («normalised root squared error», nRSE) hervorgehoben wird. So konnte man die Machbarkeit des hybriden ML-FEA Ansatzes im vereinfachten linear-elastischen Beispiel überprüfen.
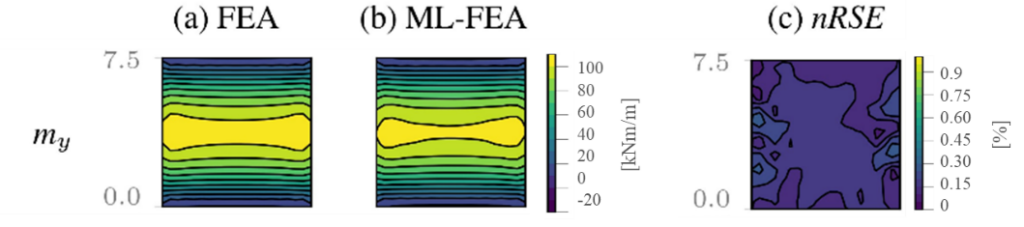
Ein Paper dazu wurde beim fib Symposium, das im Juni 2025 stattfindet, eingereicht. Dieses Paper wird hier verlinkt werden sobald es online verfügbar ist – bis dann können Sie sich gerne bei mir direkt melden, ich erläutere Ihnen gerne die weiteren Details. Bleiben Sie daran für weitere Erkenntnisse in Machine Learning für die Finite Elemente Analyse von Stahlbetontragwerken!
Vera Balmer
Literatur
Link to English version: Predictive Structural Assessment of Concrete Frame Bridges using Machine Learning
Viele Brücken in Europa und darüber hinaus erreichen das Ende ihrer ursprünglichen Lebensdauer. Dies stellt eine grosse Herausforderung dar, da die Sicherheit von Tausenden alternder Bauwerke in kurzer Zeit überprüft werden muss. Tragwerkseigentümer müssen ihre Ressourcen für die Instandhaltung strategisch einsetzen, während sie gleichzeitig Budgetbeschränkungen, Umweltauflagen und begrenzte personelle Kapazitäten berücksichtigen. Herkömmliche Methoden der statischen Überprüfung von Tragwerken sind jedoch zeitaufwendig, teuer und daher nicht effizient auf grosse Bestände skalierbar.
Jüngste Fortschritte im Bereich des maschinellen Lernens (ML) bieten vielversprechende Lösungen. Durch die Erstellung datengestützter Vorhersagemodelle können wir eine effiziente Vorüberprüfung ermöglichen, strukturelle Massnahmen priorisieren und Entscheidungsunterstützung im Vorgehen bei der statischen Überprüfung bieten.
In diesem Blogbeitrag stellen wir ein auf ML-basiertes Tool für die statische Vorüberprüfung von Stahlbetonrahmenbrücken vor – eine der häufigsten Brückenarten in der Schweiz. Dieser Prototyp wurde im Rahmen eines laufenden Forschungsprojekts an unserem Lehrstuhl in Zusammenarbeit mit den Schweizerischen Bundesbahnen (SBB) entwickelt. In den folgenden Abschnitten demonstrieren wir die Anwendung des Tools anhand eines Praxisbeispiels und diskutieren die praktischen Auswirkungen sowie die zukünftigen Entwicklungsmöglichkeiten. Für Interessierte bieten wir abschliessend Einblicke in die zugrunde liegende Methodik.
Anwendungsbeispiel aus dem SBB-Portfolio
Um zu demonstrieren, wie das ML-basiertes Tool eingesetzt werden kann, haben wir es auf eine bestehende Eisenbahnunterführung aus dem SBB-Brückenportfolio angewendet. Um die statische Ausnutzung einer bestehenden Rahmenbrücke abzuschätzen, können die Nutzer:innen die relevanten Brückenparameter in das Webtool eingeben oder importieren und Vorhersagen generieren (siehe Abbildung 1). Für eine erste Schätzung benötigt das Modell lediglich eine geringe Anzahl an geometrischen Dimensionen als Eingabe: Spannweite, Plattendicke sowie die Höhe und Breite der Brücke. Um die Vorhersagegenauigkeit zu erhöhen, können Nutzer:innen auch zusätzliche strukturelle Details wie die Bewehrungsanordnung, Materialeigenschaften und Lastanordnung einfügen.
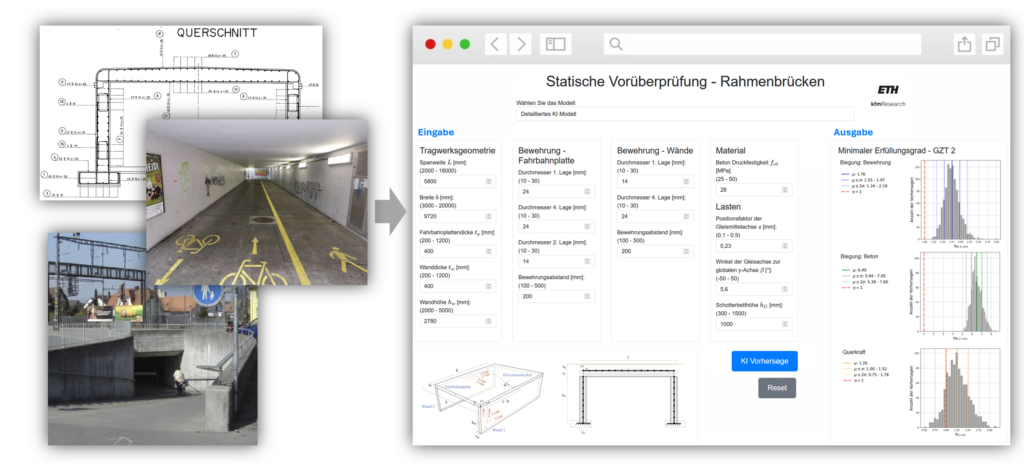
Abbildung 2 zeigt die Ergebnisse, die das ML-Modell für das Anwendungsbeispiel prognostiziert. Die Ausgabe besteht aus drei prädiktiven Verteilungen, die die geschätzten Erfüllungsgrade η für die eingegebene Brückenstruktur darstellen. Diese Werte zeigen an, ob eine Brücke die Tragsicherheitsanforderungen gemäss den Schweizer Normen für den Grenzzustand der Tragfähigkeit (GZT) erfüllt. Das zugrunde liegende datengestützte Modell wurde so trainiert und validiert, dass die Vorhersagen gut mit detaillierten mechanischen Strukturanalysen übereinstimmen.
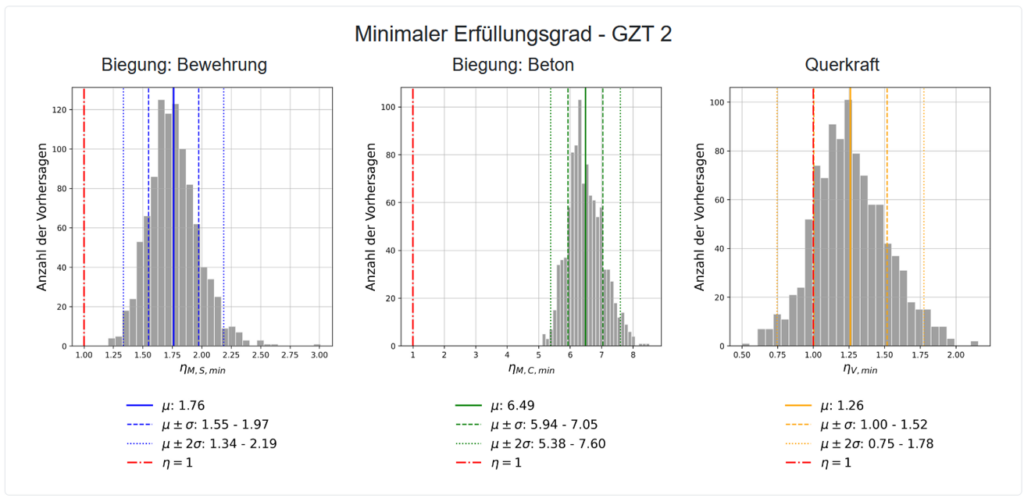
Für diese spezifische Brücke prognostiziert das ML-Modell, dass die Nachweise der Biegebeanspruchung die erforderlichen Erfüllungsgrade mit hoher Sicherheit erfüllen (η >> 1). Bei der Schubüberprüfung bleibt der beste Schätzwert (d. h. der Mittelwert der prädiktiven Verteilung μ) zwar über dem Grenzwert für die strukturelle Sicherheit (η = 1), das Modell zeigt jedoch eine gewisse Unsicherheit. Dies ist an der Streuung der prädiktiven Verteilung erkennbar, bei der ein kleiner Teil der Verteilung auch unter die Schwelle von 1 fällt. Das Tool identifiziert somit die Schubüberprüfung als kritisch. Aufgrund dieser Unsicherheit und des prognostizierten Werts, der nahe an der Schwelle von 1 liegt, empfiehlt das Tool die Anwendung detaillierter Analysemethoden, um die Tragsicherheit zu überprüfen. Anstatt vereinfachte Analysemethoden anzuwenden, die möglicherweise zu konservativ sind, um die Tragsicherheit der Struktur nachzuweisen.
Die Empfehlung des Tools für eine verfeinerte Strukturmodellierung und -analyse wurde durch eine anschliessende nichtlineare Finite-Element-Analyse (FEA) des Beispieltragwerkes bestätigt, die die Genauigkeit der Erfüllungsgradprognosen des ML-Modells für dieses Anwendungsbeispiel validiert. Zum Vergleich: Die Brücke wurde zuvor von einem Ingenieurbüro mit herkömmlichen linearen FEA-Methoden analysiert. Diese Berechnung ergab unzureichende Erfüllungsgrade, was zu einer Empfehlung für Verstärkungsmassnahmen führte, die auf etwa CHF 300’000 geschätzt wurden. Dieses Beispiel verdeutlicht den Vorteil des Vorhersagetools. Durch die Nutzung des ML-basierten Abschätzungstools konnte von Anfang an die passende verfeinerte Analysemethode ausgewählt werden. Die nichtlinearen FEA-Ergebnisse bestätigten letztendlich die Tragsicherheit und verhinderten unnötige Kosten und ressourcenintensive Verstärkungsmassnahmen.
Praktische Auswirkungen und Entwicklungspotenzial
Ein solches ML-basiertes Vorhersagetool soll nicht die mechanische Tragwerksanalyse ersetzen, sondern als effiziente und wirtschaftliche Abschätzungsmethode dienen. Das Anwendungsbeispiel veranschaulicht, dass die Prognosen des Modells eine Entscheidungsunterstützung bieten, die Tragwerkseigentümern hilft, die nächsten Schritte für die Strukturen innerhalb ihres Portfolios zu bestimmen. Es hilft auch Ingenieur:innen dabei, das geeignete Mass an Modellierungsgenauigkeit und Analyseaufwand für die statische Überprüfung einer spezifischen Struktur zu wählen. Wichtig ist, dass die Vorhersagen des Tools immer mit ingenieurtechnischem Urteilsvermögen interpretiert werden müssen.
Dieser Prototyp ist derzeit auf einfache Betonrahmenbrücken anwendbar. Die Methode kann jedoch auch auf andere Brückentypen, die Normen anderer Länder und zusätzliche Faktoren wie verschiedene Schadensbilder ausgeweitet werden. Die Weiterentwicklung des Tools zielt darauf ab, die Priorisierung und Durchführung der Bauewerksüberprüfungen über grosse Bestände hinweg effizienter zu gestalten und Ressourcen dort einzusetzen, wo sie benötigt werden.
Wie das ML-Modell entwickelt wurde
Basierend auf dem umfangreichen Rahmenbrückeninvetar der Schweizerischen Bundesbahnen (SBB) haben wir gängige Stahlbetonrahmenbrücken parametrisiert und eine parametrische Berechnungspipeline entwickelt, welche detaillierte nichtlineare FEA-Simulationen durchgeführt, um einen Datensatz von Erfüllungsgraden zu erstellen. Auf Basis dieses Datensatzes haben wir dann ein ML-Modell (speziell ein Bayessches neuronales Netz [1]) trainiert, um die Abbildung zwischen Brückenparametern und Erfüllungsgraden zu erlernen (siehe Abbildung 3). Dies ermöglicht es dem Modell, die Daten im hochdimensionalen Parameterraum zu interpolieren und Vorhersagen für Brücken zu treffen, die noch nicht analysiert wurden. Im Gegensatz zu Standard-Neuronalen Netzen schätzt der Bayessche Ansatz auch die Unsicherheit der Vorhersage. Sowohl die für die Datengenerierung verwendete parametrische Pipeline als auch das trainierte ML-Modell wurden anhand von Parameterstudien und bestehenden Strukturen (wie im oben gezeigten Anwendungsbeispiel) validiert. Die Vorhersagegenauigkeit des Modells wurde mit unbekannten Daten getestet, und die Unsicherheitsabschätzung wurde so kalibriert, dass akkurate Konfidenzintervalle gewährleistet sind.
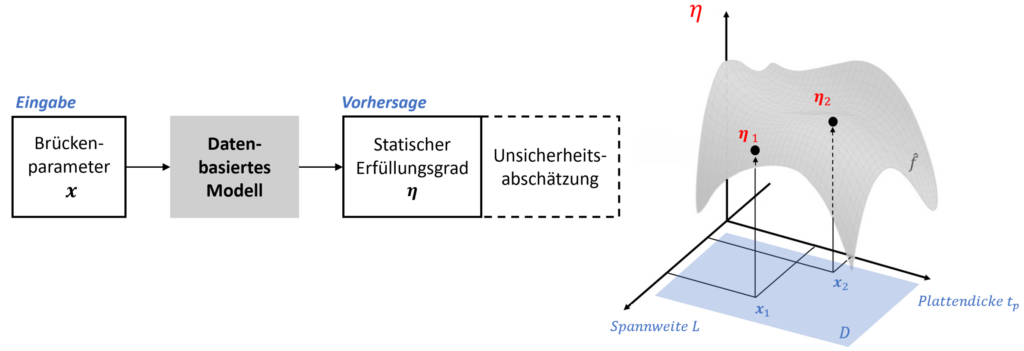
Wollen Sie mehr erfahren?
Haben Sie Fragen oder Anmerkungen zu diesem Projekt? Zögern Sie nicht, sich an Sophia Kuhn zu wenden.
Sophia Kuhn
Literatur
| [1] S. V. Kuhn, M. Weber, A. Binggeli, M. A. Kraus, F. Perez-Cruz, W. Kaufmann, Predictive structural assessment of concrete frame bridges with bayesian deep learning, manuscript to be submitted for publication (2025). |
Link to English version: Grammars for Strut-and-Tie Models Explained
Fachwerkmodelle dienen im Stahlbetonbau häufig als vereinfachte, sichere und meist händische Entwurfsmethode für Balken oder Wände. Um ein Fachwerkmodell herzuleiten brauchen Ingenieur:innen meist viel Zeit und Fachwissen, weshalb sich Forscher:innen seit Jahrzehnten mit anderen Möglichkeiten für die Fachwerkgenerierung beschäftigen. In meinem letzten Blogpost, habe ich die zwei Hauptansätze zur automatisierten Generierung von Fachwerkmodellen für Stahlbetontragwerke und ihre Vor- und Nachteile vorgestellt. Die kontinuierliche Topologieoptimierung hat das Ziel, möglichst viel Material zu entfernen, um die Masse oder das Volumen einer Struktur zu minimieren, während gleichzeitig strukturelle Bedingungen (z.B. Fliessgrenze der Bewehrungsstäbe) erfüllt werden müssen. Daraus muss dann ein Fachwerk abgeleitet werden. Bei dieser Methode ist es jedoch schwierig, ausführungstechnische Aspekte (z.B. Präferenz für eine regelmässige Anordnung der Bewehrung oder orthogonale Bewehrung) adequat zu berücksichtigen. Die diskrete Layoutoptimierung zielt darauf ab, eine verbundene Struktur auf Grundlage vordefinierter gitterartiger Knotenpunkte unter bestimmten strukturellen Bedingungen zu finden. Diese Methode hat jedoch Schwierigkeiten, benutzerspezifische Anpassungen zu berücksichten. Aufgrund dieser Nachteile konnten sich beide Methoden bisher noch nicht in der Praxis durchsetzen.
Um diese Forschungslücke anzugehen, haben wir einen Ansatz basierend auf Regeln und Grammatik entwickelt. Inspiriert von der theoretischen Informatik und formalen Sprachen, wurde das Konzept der Grammatik bereits auf Design-, Architektur- und Ingenieursanwendungen übertragen. Fachwissen und Präferenzen können somit in die Regeln integriert werden, die unterschiedliche Designs generieren können. Zuerst möchten wir dieses Konzept anhand eines einfachen Beispiels aus der formalen Sprache veranschaulichen. Sogenannte kontextfreie Grammatiken bestehen aus den Symbolen S (Startsymbol), P (Satz an Produktionsregeln), T (Terminalsymbole, Generierung stoppt; hier mit einem Rechteck dargestellt) und V (Nichtterminalsymbole, Generierung geht weiter; hier mit einer Ellipse dargestellt), siehe Abb. 1. Angenommen wir wollen einen Satz generieren, dann muss jede rechte Seite einer Regel im Generierungsprozess ein Nichtterminalsymbol (linke Seite der Regel) ersetzen. Wir beginnen mit der Regel S → Subjekt-Verb-Objekt. Als nächste Regeln ersetzen wir Subjekt durch «Die Studentin» usw. bis wir keine Nichtterminalsymbole mehr übrig haben und den Satz «Die Studentin liest ein Buch» gebildet haben.
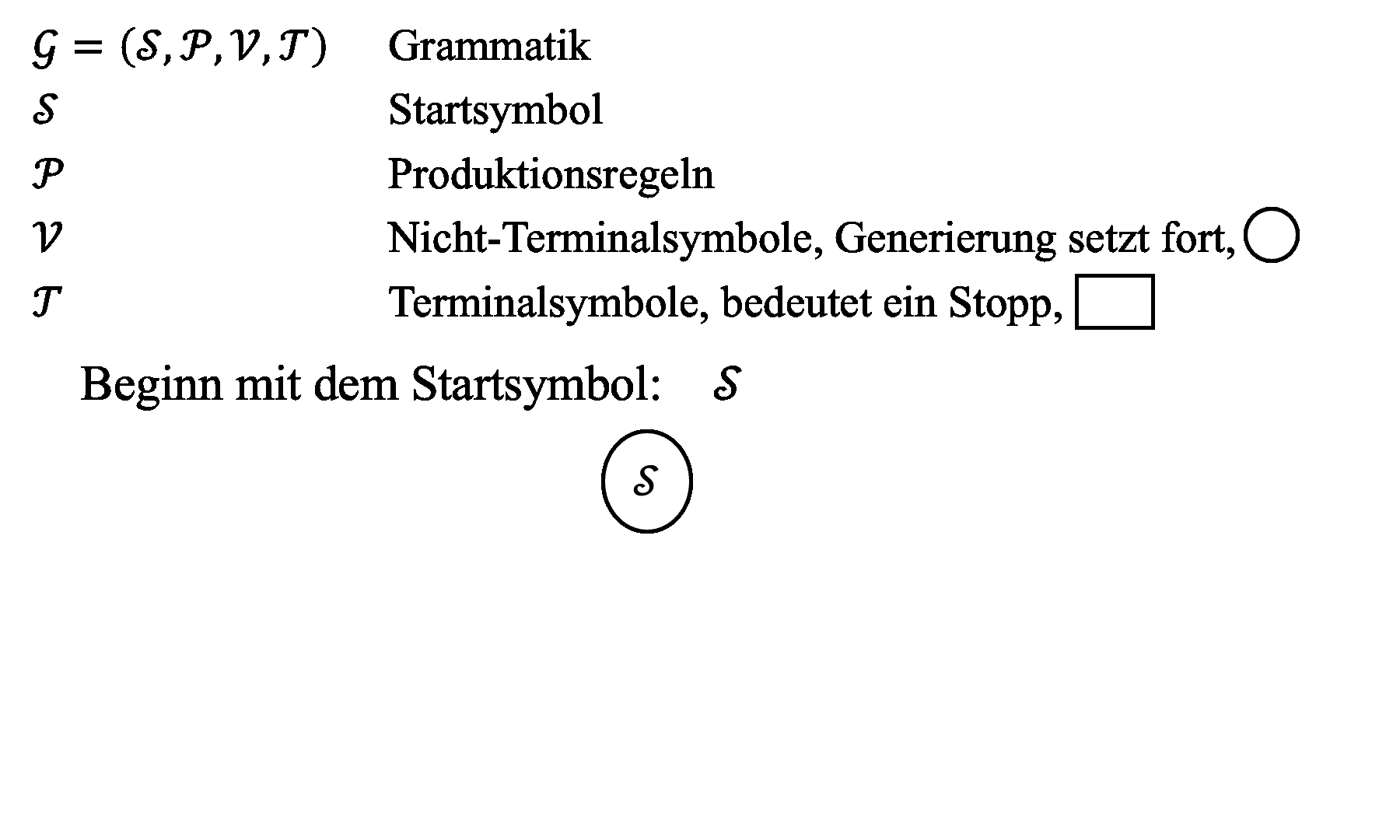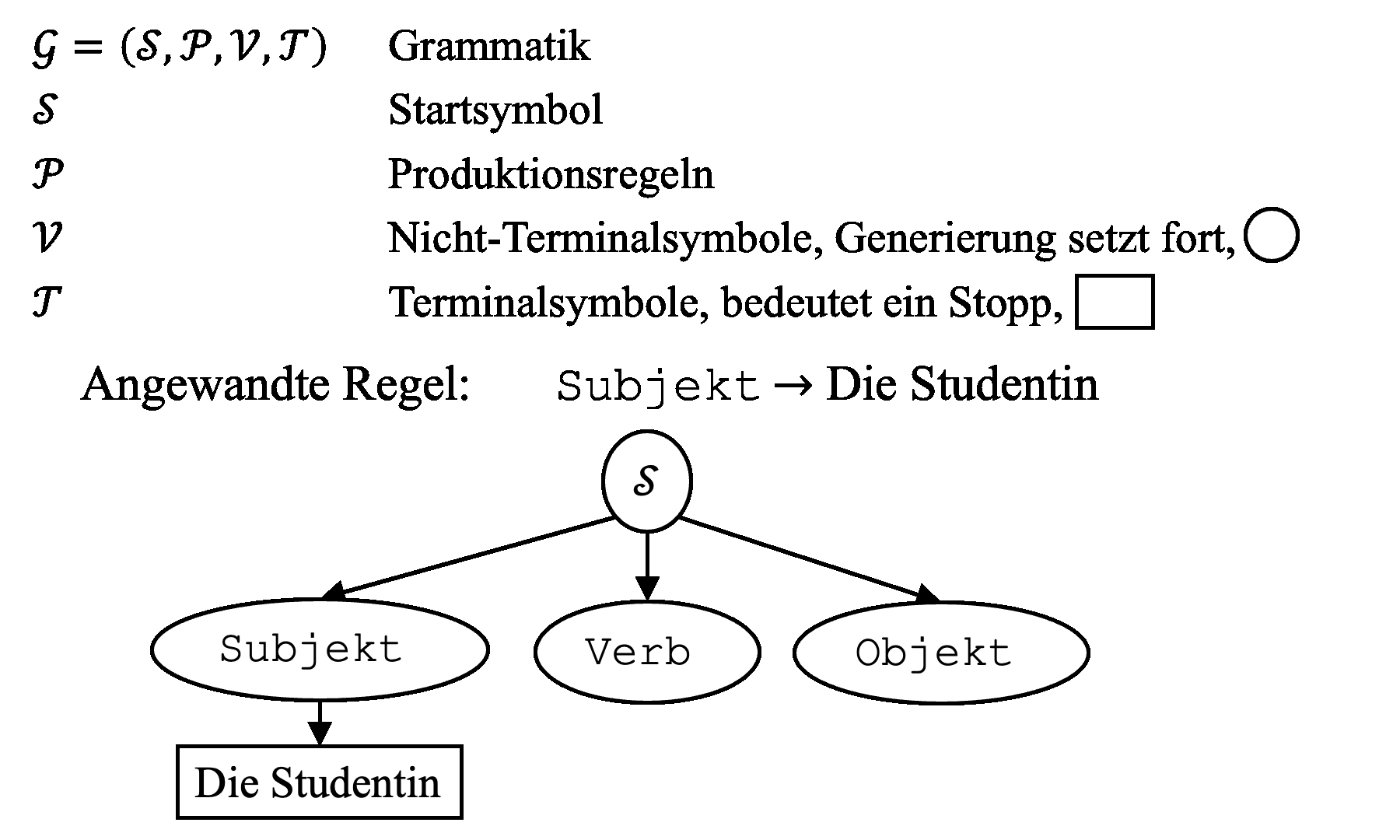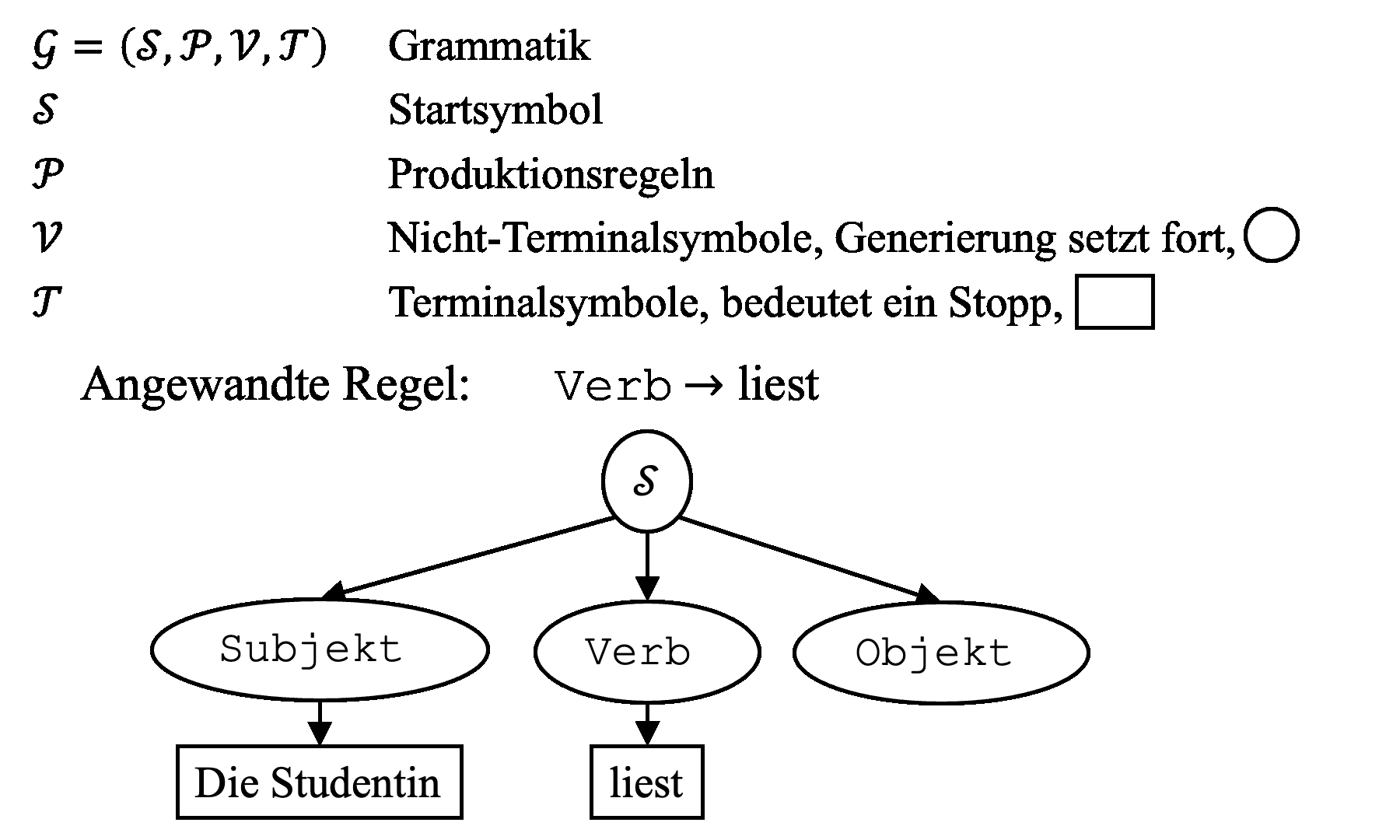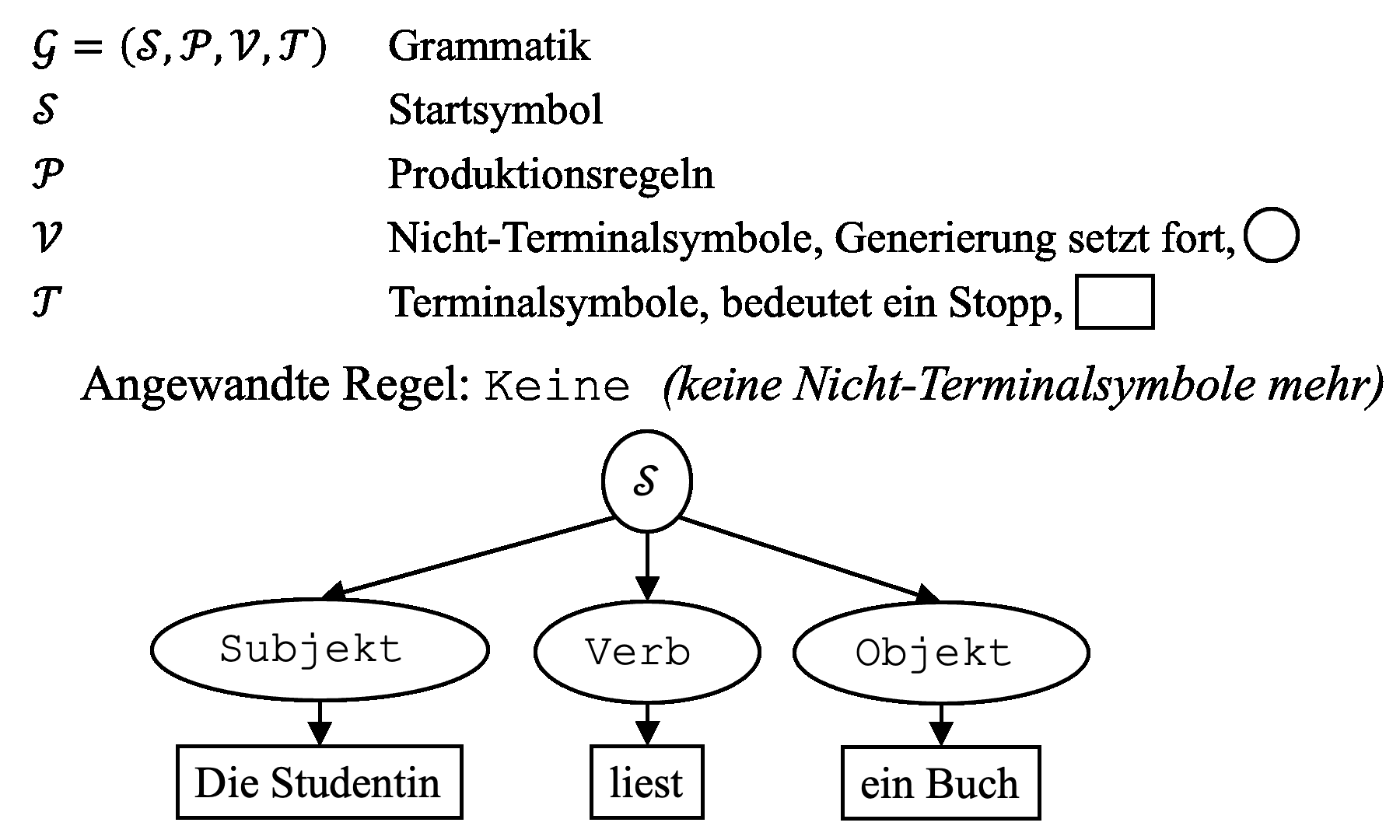
Dieses Konzept wurde auch im generativen Design angewendet. Unsere Forschungsinteressen lagen dabei hauptsächlich darin, ob man mit einem solchen Ansatz Fachwerkmodelle generieren kann und ob diese generierten Fachwerkmodelle praktischer als optimierungsbasierte Vorschläge sind.
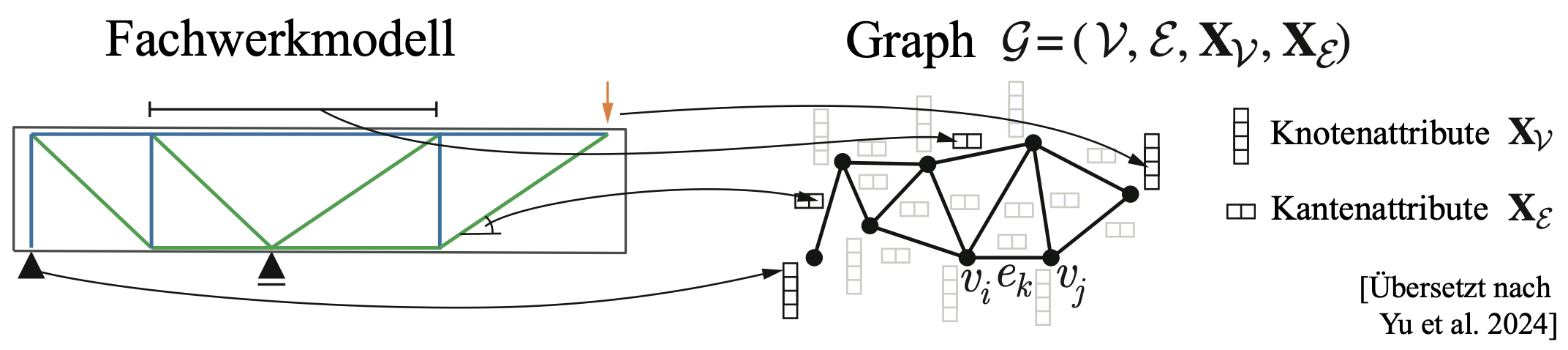
Als erster Schritt, wird das statische Problem als Graph dargestellt (Abb. 2). Wir sind normalerweise mit euklidischen Daten vertraut, welche man in Matrixform darstellen kann. Wenn wir jedoch komplexere Zusammenhänge von Daten (z.B. hierarchische Strukturen oder Abhängigkeiten) erfassen möchten, können wir nicht-euklidische Darstellungen wie Graphen, Gruppen oder Zellen verwenden. Darunter sind Graphen für uns vorteilshaft, da sie strukturierte Daten mittels Knoten und Kanten effizient darstellen können. Demnach kann man ein Fachwerkmodell einfach in eine Graphrepräsentierung umwandeln, indem die Knoten des Fachwerkes die Knoten des Graphen werden und die Druck- und Zugstäbe die Kanten. Dadurch erhalten wir einen Graph mit den gleichen Verbindungen wie das Fachwerk. Jedoch können wir aufgrund der Graphrepräsentierung nicht mehr die typische matrixbasierte statische Berechnungsmethode anwenden, um die Kräfte der Kanten zu erhalten. Darum verwenden wir die Gleichgewichtsbedingunen in den Knoten, um das statische Gleichgewicht zu finden. Für die computergestütze Implementierung, kann man zusätzliche Informationen wie Länge und Winkel einer Kante als Knoten- oder Kantenattribute hinzufügen.
Die Hauptschwierigkeit des grammatikbasierten Ansatzes besteht in der Herleitung der Regeln. Der Satz an Regeln sollte allgemein genug sein, um eine Vielzahl von verschiedenen Fachwerkmodelle zu generieren, aber auch spezifisch genug, um bestimmte bauliche und ingenieurtechnische Einschränkungen zu berücksichtigen, wie z.B. die Einhaltung von Mindestfachwerkwinkeln. Um diese Regeln herzuleiten, ist demnach ein gewisses geometrisches und statisches Verständnis erforderlich. Einzelheiten zu solchen Regeln finden Sie in unserem kürzlich veröffentlichten Fachzeitschriftenartikel [1], wovon einige Beispiele in Abb. 3.
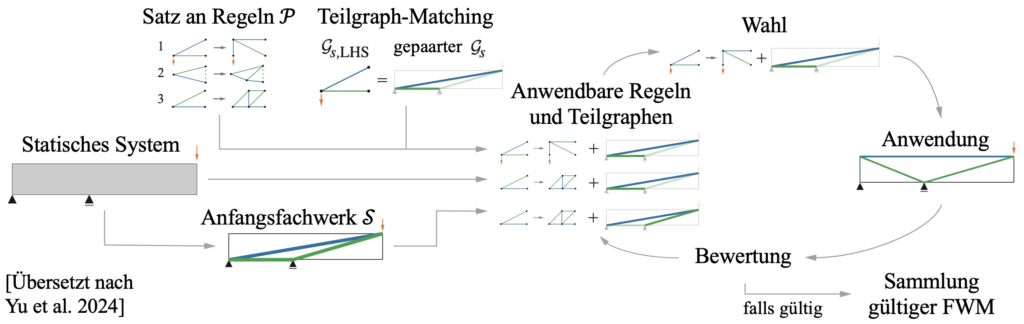
Sobald die Regeln definiert sind, folgt das Verfahren zur Generierung der Fachwerkmodelle demselben Vorgehen zur Generierung von Sätzen, siehe Abb. 3. Ein Anfangsfachwerk (das Startsymbol) kann aus dem statischen Problem abgeleitet werden, z.B. indem die Randbedingungen miteinander verbunden werden. Im Gegensatz zur formalen Sprache, hat dieser Ansatz jedoch keine direkten Terminal- und Nichtterminalsymbole. Kanten können als Terminalsymbole festgelegt werden, um die Anzahl möglicher Generierungen zu reduzieren. Andererseits, erkennt ein Teilgraph-Matching-Algorithmus1Ein Teilgraph-Matching-Algorithmus versucht einen gegebenen Teilgraph in einem Graphen effizient zu finden. In diesem Fall, wollen wir die linke Seite einer Regel im Fachwerk finden, wo wir dann die Regel anwenden können., basierend auf dem Satz der Produktionsregeln, welche linken Seiten der Regeln im aktuellen Fachwerk gefunden werden können. Diese möglichen Kombinationen werden dem Benutzer oder der Benutzerin vorgeschlagen, welche:r dann die nächste Regel auswählen kann. Nach der Transformation des Fachwerkes mit der gewählten Regel werden einige Kennzahlen zur Beurteilung der Qualität des Fachwerks angezeigt. Diese Kennzahlen beziehen sich sowohl auf die Gültigkeit (z.B. Geometrie, Überkreuzung von Kanten und Fachwerkwinkel) als auch auf die Eignung (z.B. Komplexität der Bewehrung und Stahlverbrauch) von Fachwerkmodellen.
Die Generierung von Fachwerken mit Grammatiken wird anhand des Beispiels einer Wand mit einer Öffnung in Abb. 4 veranschaulicht, welches ein übliches Beispiel2Dieses Beispiel wurde auch in meinem letzten Blogpost besprochen. aus der Literatur ist. Zuerst wenden wir eine Regel an, welche den linken Lagerknoten über der Öffnung aufhängt. Die Parameter der Regel können angepasst werden, um die Position des neu eingeführten Knotens zu beeinflussen (vergleichen Sie den ersten Schritt jeder Lösung). Durch Variieren von Regeln und Parametern können unterschiedliche Fachwerkmodelle generiert werden. Sowohl ein einfacher und effizienter Entwurf, wie Lösung A, mit geneigter Bewehrung, wie auch ein komplexerer Entwurf (Lösung C) mit orthogonaler Bewehrung können so also mit dem grammatikbasierten Ansatz generiert werden.

Diese und weitere Beispiele [1] zeigen, dass die grammatikbasierte Generierung es erlaubt, mittels Mensch-Computer Interaktion praktischere Fachwerkmodelle als mittels optimierungsbasierten Methoden3z.B. in Mozaffari et al. 2020 zu generieren. Diese Generierung könnte jedoch mit zunehmender Komplexität des Fachwerks und der Anzahl Regeln umständlich werden. Derzeit erforschen wir deshalb alternative rechnergestütze oder KI-basierte Methoden, um den Entwurfsraum automatisierter navigieren zu können, und hoffen, Sie im Verlaufe des Jahres über Fortschritte informieren zu können. Bei Fragen oder Anmerkungen, können Sie gerne Karin Yu kontaktieren.
Karin Yu
Literatur
| [1] Yu, K. L., Kraus, M. A., Chatzi, E., Kaufmann W. (2024). Grammar-Based Generation of Strut-and-Tie Models for Designing Reinforced Concrete Structures. Computers & Structures. Volume 305. 107549. doi.org/10.1016/j.compstruc.2024.107549 |
Link to English version: Structural Testing of a CFRP-Prestressed Railway Bridge Prototype
Nach meinem letzten Blogbeitrag zur Herstellung des ersten CFK-vorgespannten Eisenbahnbrückenprototyps der Schweiz war das Projekt «Prototyp» für mich eigentlich abgeschlossen und ich habe mich darauf gefreut, mal wieder seriöse Wissenschaft aus dem Bürostuhl betreiben zu können – am liebsten etwas mit AI. Unweigerlich kam jedoch im Verlauf des Sommers die Frage auf, was wir jetzt mit diesem etwas klobigen Ding anfangen sollen: es konnte ja – Dauerhaftigkeit in Ehren – nicht für immer bei uns in der Bauhalle rumstehen. Als vertikal bepflanzbare Blumenkiste im Kaffeeraum aufstellen? Zwecks Vermarktung unseres Leuchtturmprojekts in Sachen Nachhaltigkeit ins All feuern? Mit seinen 10 t Gewicht wäre der Prototyp ja nur unwesentlich schwerer als der rote Tesla, der dort bereits seit Jahren seine Runden dreht… Nachdem beide Ideen in erster Linie aufgrund überbordender ETH-interner Bürokratie (versuch mal, in einem Bundesbetrieb die Genehmigung für einen Raketenstart zu kriegen) versenkt werden mussten, kam die Idee auf, den Prototyp auf sein Tragverhalten zu testen. Ziemlich wild, dafür hätte ja jemand einen Teststand mit 3 MN Kapazität bauen, Unmengen an Kraftmessdosen, Wegaufnehmern und Kameras herumliegen haben und bereits in der Herstellung des Prototyps optische Fasern zur Dehnungsmessung an Bewehrung und Vorspannung eingebaut haben müssen…
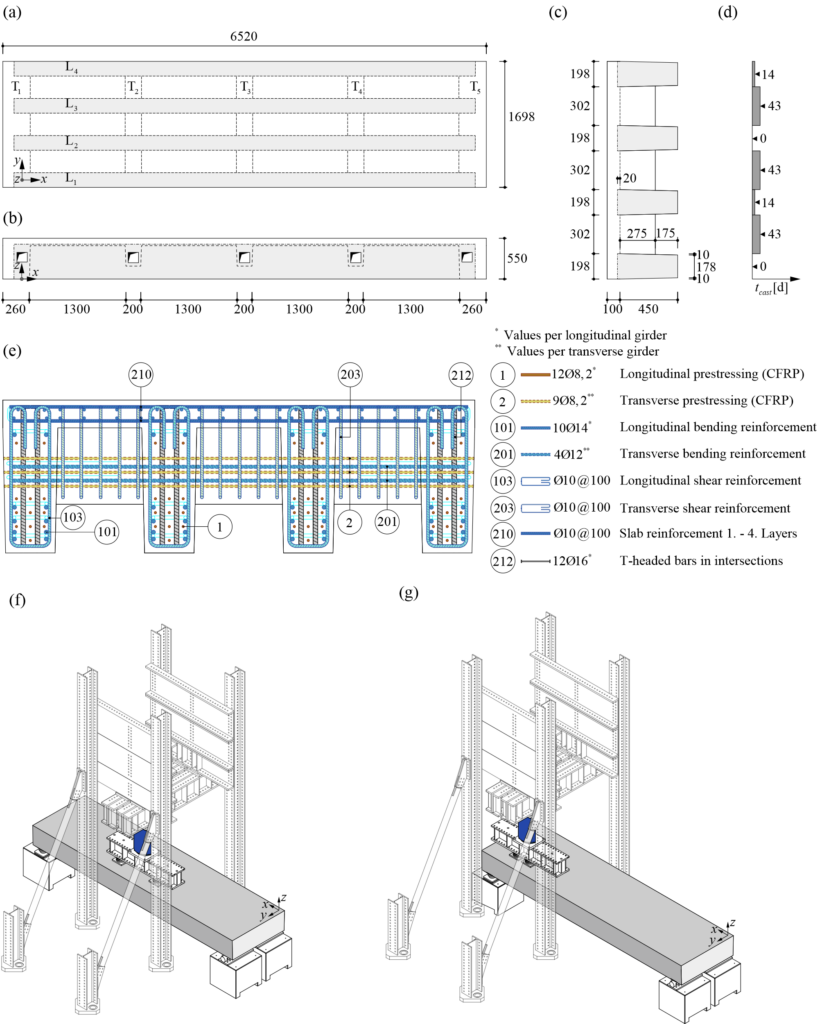
Das Ziel des Prototypversuchs war – neben dem «proof of concept» für die Herstellung – der «proof of concept» für das Tragverhalten des Werkstoffs «CFK-vorgespannter Stahlbeton» und seine Eignung für Eisenbahnbrücken. Insbesondere die folgenden Fragen waren dabei von zentraler Bedeutung:
- Funktioniert die Verankerung der im Spannbett vorgespannten CFK-Stäbe über Verbund mit dem Beton? Funktioniert sie insbesondere auch bei zyklischer und auflagernaher Belastung?
- Wie verhält sich der Verbundwerkstoff im Grenzzustand der Tragsicherheit? Erreichen wir den angestrebten Biegeversagensmechanismus «Betonversagen bei Stahlfliessen» und eine gewisse plastische Verformung in der Bewehrung trotz des spröden CFK?
- Wie verhält sich der Prototyp bei auflagernaher Belastung, was für ein Querkraftversagen stellt sich ein? Welche Druckfeldneigungen darf ich bei einem Hochleistungsbeton mit CFK-Vorspannung für den Querkraftnachweis annehmen?
Eins vorweg: Im Rahmen dieses Blogbeitrags kann ich natürlich nicht im Detail auf diese Fragen eingehen. Für ausführliche Versuchsauswertungen und -interpretationen sei die interessierte Leser:in auf unsere wissenschaftlichen Publikationen zum Thema (z.B. hier) verwiesen. Doch der Reihe nach: Abbildung 1 gibt einen Überblick über den Prototyp und die Versuchsanordnungen des Biege- und Querkraftversuchs. Der aus vier CFK-vorgespannten Längs- und drei Querträgern (im Feld) bestehende Prototyp wurde zunächst in im Querschnitt exzentrischer Vier-Punkt-Biegung belastet. Die Lasten standen dabei auf dem zweiten von vier Längsträgern. Nach 60’000 Lastzyklen auf drei verschiedenen Lastniveaus wurde der Prüfkörper zu Bruch gefahren, wobei der Versagensmechanismus ein Betonbruch bei Fliessen der Stahlbewehrung und anschliessendem (gut hörbaren) Reissen erster CFK-Stäbe im Feld war. Anschliessend wurde der Prüfstand etwas modifiziert, und in einem weitgehend intakten Bereich des Prüfkörpers (der um 180° gedreht wieder eingebaut wurde) ein Querkraftversuch durchgeführt, bei dem die Last auflagernah aufgebracht wurde.
Videos 1 (Zeitrafferaufnahme) und 2 (Versuchsende) zeigen Ausschnitte aus dem Biegebruchversuch. Wichtig dabei ist zu betonen, dass trotz des Betonbruchs in der Biegedruckzone (siehe Video 2), der sich nahezu über die gesamte Breite des Prüfkörpers erstreckte, und trotz des Bruchs einzelner Spannstäbe (Video 2 mit Ton), kein totaler Kollaps des Prototyps stattgefunden hat.
Zusammen mit Abbildung 2 (Last-Verformung in Biege- und Querkraftversuch, Bild des Schubversagens) geben die Videos einen Einblick in einige, aber nicht alle der eingangs formulierten Fragestellungen:
- Die Vorspannung blieb während der gesamten Versuchsserie intakt, was exemplarisch am Wiederaufrichten des Prüfkörpers nach dem Biegeversuch (siehe Video 1) festgemacht werden kann. Inwieweit sich die Verankerungszonen der Spannstäbe aufgrund der zyklischen und auflagernahen Belastung verlängert haben, liess sich leider nicht abschliessend feststellen, da die optischen Fasern auf den gespannten CFK-Stäben der Längsträger während der Versuche nicht funktioniert haben.
- Der angestrebte Biegeversagensmechanismus wurde erreicht. In drei von vier Längsträgern kam der Bewehrungsstahl im Biegeversuch ins Fliessen, was eine Umverteilung von Kräften im Prüfkörper zur Folge hatte. Abbildung 2 (a) zeigt (i) wie alle vier Längsträger aktiviert wurden, und (ii) das erhebliche Verformungsvermögen nach Erreichen der Maximallast (Betondruckzonenversagen), bei welcher kein signifikanter Abfall der Last im verformungsgesteuerten Test-setup stattfand. Stattdessen konnte sich das System bei ungefähr gleichbleibender Last noch erheblich verformen, bevor der Test abgebrochen wurde.
- Auch bei auflagernaher Belastung wurden alle vier Längsträger signifikant aktiviert, wie dem Last-Verformungsdiagramm in Abbildung 2 (b) entnommen werden kann. Wie erwartet, fand das Schubversagen im belasteten Träger L2 statt, bei einer Querkraft im Längsträger von ca. 900 kN. Daraus folgt, dass die Bügel im Fliessen waren, das Versagen fand jedoch wie in Abbildung 2 (c) zu sehen ist im Beton statt, und zwar bei einer ziemlich steilen Druckfeldneigung von ca. 35-40°. Es stellten sich folglich nicht wie üblicherweise angenommen «rotierende Risse» mit zum Schluss sehr flachen Neigungen (vergleiche erlaubte Druckfeldneigungen vorgespannter Tragwerke gem. SIA 262) ein, was für Hochleistungsbetone aufgrund ihrer kleinen Rissrauigkeit nicht unüblich ist.
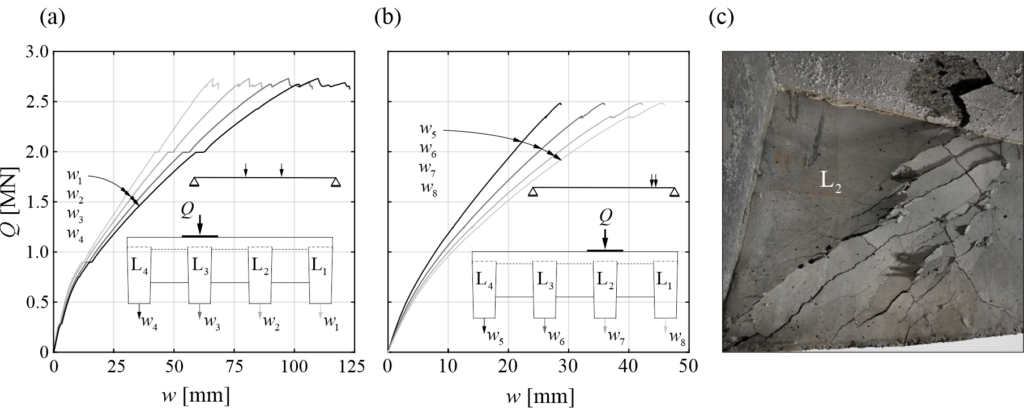
Aus Sicht des Projektteams ist der «proof of concept» gelungen. Das Biegetragverhalten ist wie antizipiert, der Bewehrungsstahl bringt eine gewisse plastische Verformungskapazität in das System. Die Vorspannung ist robust, muss aber weiter im Detail (mit funktionierenden faseroptischen Dehnungsmessungen) untersucht werden. Dasselbe gilt für das Schubtragverhalten. Was bedeutet das? Im Rahmen der momentanen Projektphase «Wissenschaftliche Aufarbeitung» (Phase 3 von 5 auf dem Weg zum tatsächlichen Bau einer CFK-vorgespannten Bahnbrücke auf dem SBB-Netz) stehen weitere Versuche an; besonders spannend werden dabei die statischen und zyklischen Schubversuche an einzelnen CFK-vorgespannten T-Trägern. Parallel zu den Versuchsserien beginnen wir nun mit der mechanischen Modellierung und den Nachweiskonzepten. Ausserdem bedeutet es, dass das mit mir und der AI weiter warten muss… stay tuned!
Andreas Näsbom
Literatur
| [1] | A. Näsbom, K. Thoma and W. Kaufmann, “Construction and testing of a CFRP-prestressed railway bridge prototype”, in IABSE Symposium Manchester 2024, Manchester, Apr. 2024. |
Link to English version: 3D-Apps with AR capabilities for teaching structural concrete
Einführung
Zum Erlernen der Grundlagen der Tragwerksplanung gehört nicht nur das Verständnis mathematischer Formeln und mechanischer Modelle, sondern auch deren Interaktion mit dem realen 3D-Raum. Unsere Professur hat gute Erfahrungen mit der Einführung von Webanwendungen gemacht, die unseren Studierenden helfen, die wichtigsten Prinzipien der Vorlesungen zu Stahlbeton zu verstehen. Diese Anwendungen konzentrieren sich jedoch hauptsächlich auf die abstrakte Darstellung des Inhalts durch 2D-Zeichnungen, Diagramme und Text. Zusätzlich bieten sie die Möglichkeit, mit den zugrundeliegenden mechanischen Modellen zu interagieren, indem die geometrischen, materiellen oder anderen Eigenschaften mit Hilfe von Schiebereglern und Texteingabefeldern verändert werden. Während dieser Ansatz für verschiedene Lehrinhalte geeignet ist, wie die 17 Anwendungen zeigen, die bereits in unseren Bachelor-Kursen eingesetzt werden, haben wir auch Beispiele gefunden, die von einem anderen Präsentationsstil profitieren würden. Es wurden drei Aspekte der bisherigen Apps identifiziert, die uns zur Arbeit an einer neuen Generation von Apps motiviert haben. Diese sind:
- Abstrakte Darstellung von Konzepten mit Hilfe von 2D-Zeichnungen oder Diagrammen. Dies kann es den Studierenden erschweren, die gezeigten Konzepte mit Beispielen aus dem wirklichen Leben in Verbindung zu bringen.
- Viele verschiedene Eingabemöglichkeiten wie Schieberegler, Textfelder und mehrere Ausgabeziffern können für die Studierenden überwältigend sein
- Die Apps sind in verschiedenen Programmierumgebungen geschrieben, was für unerfahrene Lehrkräfte eine Hürde für die Anpassung oder Erstellung neuer Apps darstellen kann.
Um diese drei Punkte anzugehen, basiert die neue Generation von Apps auf den folgenden drei Ideen:
- Die Darstellung von Geometrie im 3D-Raum sowohl in einer virtuellen Umgebung als auch verankert in der realen Welt mit Hilfe von Augmented-Reality-Funktionen.
- Eine klare Benutzer-/Studierendenführung durch die Anwendung, um zu vermeiden, dass die Studierenden von der Komplexität des Modells überwältigt werden.
- Ein möglichst simples Implementierungskonzept im Backend, das die einfache Manipulation bestehender Beispiele und die schnelle Erstellung neuer Beispiele ermöglicht.
Es ist zu betonen, dass das neu entwickelte Framework für 3D-AR-Apps nicht dazu gedacht ist, die derzeit an unserer Professur verwendete Sammlung von Apps zu ersetzen. Vielmehr ist das Ziel, diese dort einzusetzen, wo die aktuelle Generation von Apps nicht geeignet ist.
Prototyp
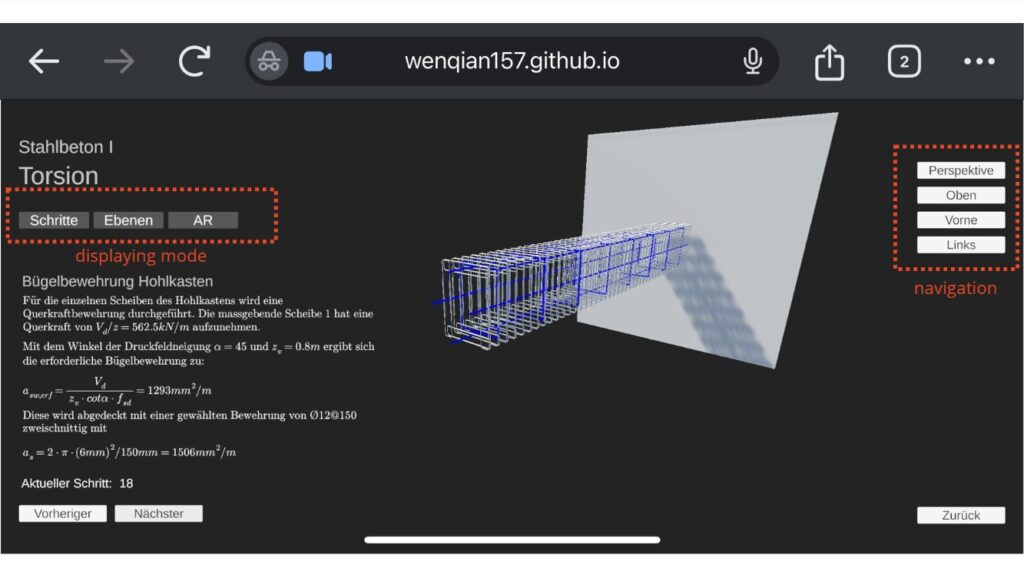

Unser erstes Beispiel basiert auf einer der Übungen in der Vorlesung „Stahlbeton 1“, die sich mit der Bemessung eines Torsionsbalkens mithilfe von Fachwerkmodellen beschäftigt. Der Benutzer kann die App mit den meisten gängigen Browsern auf einem mobilen Gerät oder einem Computer aufrufen. Besuchen Sie dazu einfach den angegebenen Link oder scannen Sie den QR-Code mit der Kamera.
Sobald die App gestartet ist, können Sie ihre Funktionen über die Benutzeroberfläche erkunden.
Für die AR-Funktion gewähren Sie den Kamerazugriff, wenn Sie dazu aufgefordert werden, und scannen dann einen Aruco 6×6-Marker, um die Augmented-Reality-Funktionen zu nutzen.
Backend-Implementierungsrahmen
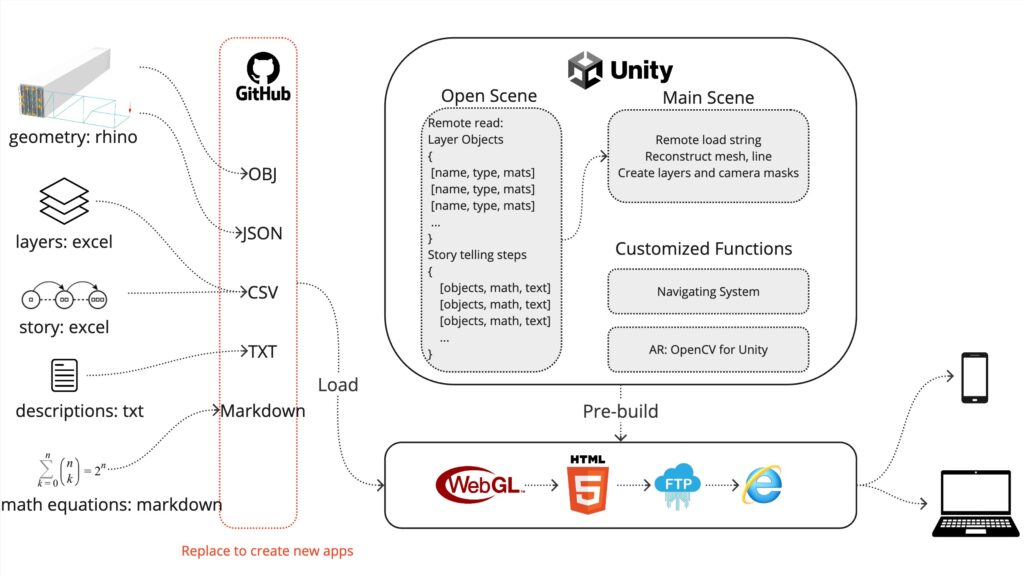
Der Grundgedanke des Frameworks ist, dass es auch für App-Entwickler, die nicht mit Unity vertraut sind, leicht zu verwenden und anzupassen ist. Daher wurden weit verbreitete Dateitypen als Input gewählt. Im aktuellen Stand der Projektimplementierung sind dies die folgenden rohen Eingabedateien:
– 3D-Geometrie (.3dm)
– Ebenen-Informationen (.xlsx)
– Ablaufinformationen (.xlsx)
– Schrittbeschreibungen (.markdown)
Das Framework besteht aus drei Hauptteilen. Der erste Schritt besteht darin, alle rohen Eingabedateien in Formate zu konvertieren, die leicht über das Internet kommuniziert werden können, wie OBJ, JSON und CSV. Im zweiten Schritt wird ein Unity-Projekt entworfen, das diese Materialien empfängt und in 3D-Geometrie, Diagramme oder mathematische Gleichungen umwandelt. Es wurde ein Bediensystem für Maus- und Toucheingaben in einer Browserumgebung entwickelt, das es dem Benutzer ermöglicht, die Inhalte im 3D-Raum zu erleben. Zusätzlich wird eine AR-Implementierung eingeführt, die den Studierenden helfen soll, die Geometrie im Raum zu verstehen. Der dritte Schritt umfasst die Kompilierung und Bereitstellung dieser Anwendung als Webanwendung, die dann auf einem Webserver gehostet wird, damit die Benutzer darauf zugreifen können.
Falls Sie mehr über den Ablauf zum Erstellen eines neuen Beispiels erfahren wollen, werfen Sie einen Blick auf die readMe Datei.
Fazit
Die aktuelle Version der App ist ein Zwischenstand der Ideen und stellt Fortschritte des Teams in den letzten Monaten dar. Wir wollen die Stabilität und die Benutzerfreundlichkeit der interaktiven Funktionen testen und die Kompatibilität mit einer Vielzahl von Geräten sicherstellen, bevor wir eine robuste Version für die Studierenden freigeben. Das Hauptziel der nächsten Phase ist die Erweiterung des Projekts durch weitere Beispiele.
Wir laden Sie ein, den ersten Prototyp der App auf unserer Website zu testen und würden uns freuen, wenn Sie uns Ihre Meinung mit Hilfe dieses Feedback-Fragebogens mitteilen würden.
Paul Merz and Wenqian Yang
Link to English version: Effects of concrete floor slab requirements
Es ist fast ein Jahr her, seit wir in einem Blogbeitrag erläutert haben, wie die digitale Fabrikation die Verbreitung von statisch effizienten Betondecken fördern könnte und so einen Beitrag zur Verminderung der negativen ökologischen Auswirkungen der Bauindustrie leisten. Seitdem haben wir im Rahmen desselben Forschungsprojekts eine Studie über die Anforderungen an Betondecken durchgeführt und freuen uns, in diesem Blogbeitrag einige Ergebnisse daraus vorstellen zu können. Die Studie wurde auf dem fib PhD-Symposium 2024 in Budapest vorgestellt (ein Blogbeitrag zu dieser Konferenz befindet sich hier) und mit einer “special mention” ausgezeichnet. Weitere Details finden Sie im Konferenzbeitrag mit dem Titel „Correlations of requirements and performance metrics for concrete floor slabs“ von Rebecca Ammann (der Autorin dieses Blogposts), Dr. Karel Thoma, Prof. Dr. Jaime Mata-Falcón und Prof. Dr. Walter Kaufmann.
In akademischen Arbeiten zu statisch effizienten Betondecken werden oft Einsparpotentiale ausgewiesen, bei welchen es fraglich ist, ob diese in realen Anwendungen erzielt werden können: Einerseits werden in den meisten Studien idealisierte Grundrisse betrachtet, welche nur bedingt repräsentativ für reale Projekte sind. Andererseits werden Anforderungen, welche in der Praxis häufig massgebend sind (zum Beispiel bezüglich Brandschutz oder Schallschutz) in akademischen Arbeiten oft vernachlässigt. Solche Anforderungen können nicht nur für die Entwicklung und die Untersuchung von neuen Deckensystemen entscheidend sein (was ein Ziel dieses Forschungsprojekts ist), sondern auch die Effizienz von konventionellen Betondecken einschränken. Daher sehen wir es als wichtig an, die Auswirkungen dieser Anforderungen bei Betondecken systematisch zu untersuchen.
Da es zahlreiche Anforderungen gibt und die Auswirkungen einer Anforderung stark vom betrachteten Beispiel abhängen, haben wir hierfür eine Datengenerierungspipeline entwickelt. Mit dieser Pipeline können die Auswirkungen verschiedener Anforderungen schnell, automatisiert und objektiv für eine Vielzahl von Beispielen bewertet werden. Eine schematische Darstellung der Datengenerierungspipeline, die in Python mit einer Schnittstelle zur Software RFEM 6 implementiert wurde, ist in Abbildung 1 zu sehen: Die Eingabedaten beinhalten Angaben zur Geometrie der Betondecke, den Lasten, den Materialeigenschaften und den zu berücksichtigenden Anforderungen. Für jeden Satz von Eingabedaten wird eine Finite-Elemente-Analyse (FE-Analyse) durchgeführt. Basierend auf den FE-Ergebnissen wird dann iterativ ein Bewehrungslayout entwickelt. Sobald ein Bewehrungslayout gefunden wurde, welches konstruierbar ist und mit welchem alle notwendigen Tragsicherheitsnachweise erfüllt werden, werden die entsprechenden Kennzahlen berechnet und die Anforderungen überprüft.
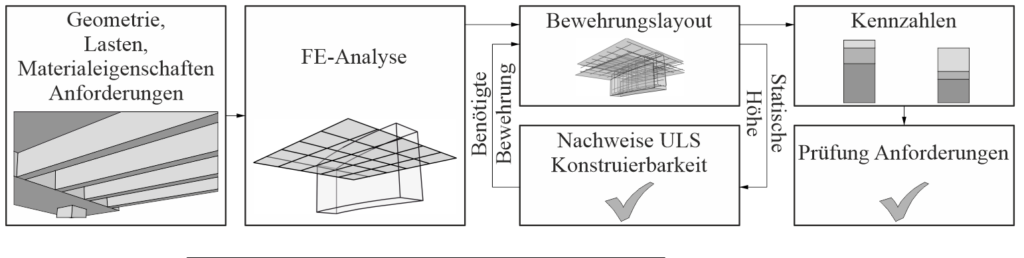
Diese Datengenerierungspipeline haben wir auf ein einfaches Beispiel mit einem quadratischen Grundriss und zwei Deckensystemen (Flach- und Rippendecke), wie in Abbildung 2 dargestellt, angewendet.
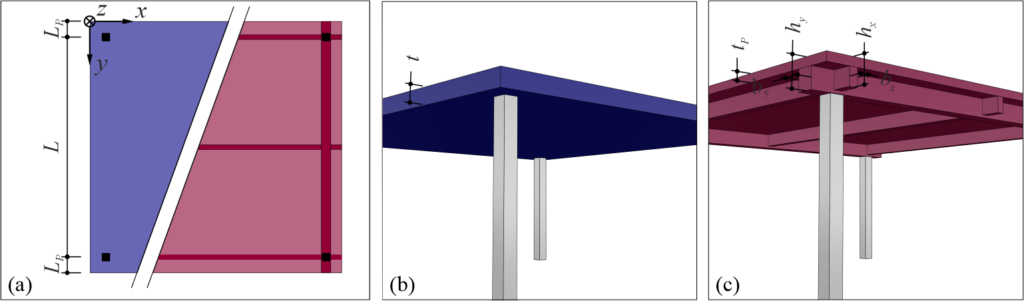
Um den Rahmen dieses Blogbeitrags nicht zu sprengen, werden im Folgenden nur die Ergebnisse bezüglich der Beschränkung der zulässigen Durchbiegungen w (Gebrauchstauglichkeit) gezeigt. Weitere Resultate sind im oben erwähnten Konferenzbeitrag zu finden.
Da die Geometrie der Betondecke Teil der Eingabedaten für die Datengenerierungspipeline ist und die optimale Geometrie nicht im Voraus bekannt ist, wurden zahlreiche mögliche Geometriekonfigurationen analysiert. In Abbildung 3 sind die Kennzahlen (relative Kosten und Treibhauspotenzial GWP) aller Konfigurationen, für welche eine Lösung gefunden wurde, für eine Spannweite L von (a) 5 m und (b) 8 m dargestellt. Die minimalen Kosten und das minimale GWP für verschiedene Spannweiten und verschiedene zulässige Durchbiegungen sind in Abbildung 3 (c) bzw. (d) dargestellt.
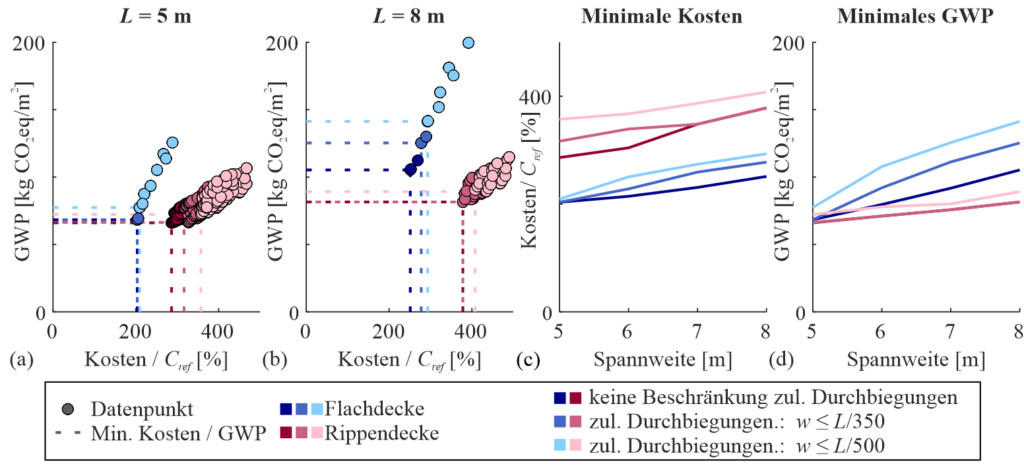
Bei Flachdecken (blau dargestellt) führt die Begrenzung der zulässigen Durchbiegungen w zu einem erheblichen Anstieg des GWP und – in geringerem Masse – der Kosten, insbesondere bei grösseren Spannweiten (Vergleich der hellblauen Linie mit der dunkelblauen Linie für eine bestimmte Spannweite). Im Gegensatz dazu ist bei Rippendecken (in rosa dargestellt) der Kostenanstieg aufgrund der Begrenzung der zulässigen Durchbiegungen (Vergleich der hellrosa Linie mit der dunkelrosa Linie für eine gegebene Spannweite) bedeutender als der entsprechende Anstieg des GWP.
Aufgrund der sehr vereinfachten Fallstudie sind die gezeigten Werte nur begrenzt aussagekräftig. Jedoch konnten wir zeigen, dass mit der Datengenerierungspipeline die signifikanten Auswirkungen von Anforderungen wie der Gebrauchstauglichkeit auf Kosten und GWP beziffert werden können. In einer Folgestudie wird diese Pipeline nun auf reale Projekte angewandt, zu welchen uns Angaben von einem Industriepartner zur Verfügung gestellt werden, wobei weitere Anforderungen und Kennzahlen berücksichtigt werden sollen. Da Anforderungen im Allgemeinen in einem sehr frühen Entwurfsstadium festgelegt werden, ohne ihre Auswirkungen zu kennen, hoffen wir, mit unserer Arbeit das Bewusstsein für die enormen Auswirkungen, die diese Anforderungen haben können, zu schärfen und die Diskussion über dieses Thema zu fördern.
Die Datengenerierungspipeline lässt sich zudem auf weitere Probleme anzuwenden, wie z. B. den Vergleich verschiedener Betondeckensysteme oder die Beurteilung der Eignung eines Systems bei verschiedenen Grundrissen – die Möglichkeiten sind schier endlos, und wir freuen uns darauf, hier zu gegebener Zeit über unsere Fortschritte zu informieren.
Rebecca Ammann
Link to English version: fib PhD Symposium Budapest 2024 – An Experience Report
Ich habe Ende August am fib PhD Symposium teilgenommen. Der fib (frz.: Fédération internationale du béton; engl.: The International Federation for Structural Concrete) organisierte diese Konferenz bereits zum 15. Mal. An dieser Konferenz präsentierten ausschliesslich PhD-Studierende und Doktorierende, die sich im weiteren Sinne mit Beton beschäftigen, ihre Arbeit. (Es gibt aber auch Konferenzen vom fib und anderen Verbänden, die sich sowohl an die Praxis als auch an die Forschung richtet.) Die über 150 Präsentationen wurden auf fünf parallele Sessions aufgeteilt, d.h. dass während den drei Tagen immer fünf Präsentationen gleichzeitig stattfanden. Die Themenvielfalt kann anhand der Titel der verschiedenen Sessions abgeleitet werden:
- Analyse, Modellierung und Bemessung von Tragwerken
- Untersuchung und Überwachung des Tragwerkzustandes
- Neuerungen im Bereich metallischer und nicht-metallischer Bewehrung
- Dauerhaftigkeit von bestehenden und zukünftigen Betontragwerken
- Neuerungen im Bereich Beton und Betontechnologie
- Brücken, Stauseen, Dämme, Tunnels und Strassenbauten
- Nachhaltigkeit von Materialien und Tragwerken, einschliesslich denkmalgeschützter Betontragwerke
- Ökobilanzierung in Verbindung mit Bemessung, Restlebensdauer
- Verbundwerkstoffe zur Verstärkung von Betontragwerken
- Instandhaltung, Sanierung und Verstärkung von Betontragwerken
- Digitalisierung – 3D-Betondruck
- Gebäude und Schalen
- Zuverlässigkeit und Risikoanalyse von Tragwerken
Teilnehmer:innen aus 72 Universitäten, verteilt über alle Kontinente, waren vertreten, wobei die Mehrheit aus Europa stammte.
Im ersten Teil meines Blogpostes werde ich vier Präsentationen/Ideen vorstellen, die ich interessant fand (und nicht aus unserer Forschungsgruppe stammen). Im zweiten Teil werde ich über die sozialen Aspekte der Konferenz berichten, die meiner Meinung nach genau so wertvoll sind wie die fachlichen Inputs.
Teil 1 – Interessante Präsentationen
Konferenzen sind nicht nur dazu da, um die eigene Arbeit zu verbreiten, sondern auch, um inspiriert zu werden von der Arbeit von anderen und diese entsprechend zu würdigen. In diesem Sinne möchte ich eine Auswahl an Vorträgen vorstellen, die bei mir einen bleibenden Eindruck hinterlassen haben:

Jens Skovgaard Larsen (Univerity of Southern Denmark / COWI [Industrial PhD Student]; Mitautoren: Henrik Brøner Jørgensen und Søren Gustenhoff Hansen) hat in seinem ersten Jahr als PhD-Student bereits mehrere Grossversuche auf einem selber entwickelten Versuchsstand durchgeführt (siehe Abbildung 1). In diesen Versuchen wird die Interaktion von Schub in und aus der Ebene von Stahlbetonplatten ohne Schubbewehrung untersucht. Er plant auch noch die Interaktion mit Momenten zu untersuchen.

Mohammed Sirage Ibrahim (TU Delft; Mitautoren: Mauro Poliotti, Yuguang Yang und Max Hendriks) hat über zwanzig 15m lange vorgespannte Betonträger auf Schub getestet (siehe Abbildung 2). Hintergrund des Projekts ist der Fakt, dass es in den Niederlanden viele bestehende Brücken gibt, die aus vorfabrizierten vorgespannten Einfeldträgern bestehen, die zu Durchlaufträgern zusammengeschlossen wurden. Bei diesen spezifischen Trägern stellen sich nun Fragen unter anderem bezüglich Schubtragverhalten. Sehr interessant finde ich an diesem Projekt auch, dass es einen blind-prediction contest beinhaltet. Emilia Andrade Borges (TU Delft) wird das Projekt weiterführen und weitere Versuche durchführen.
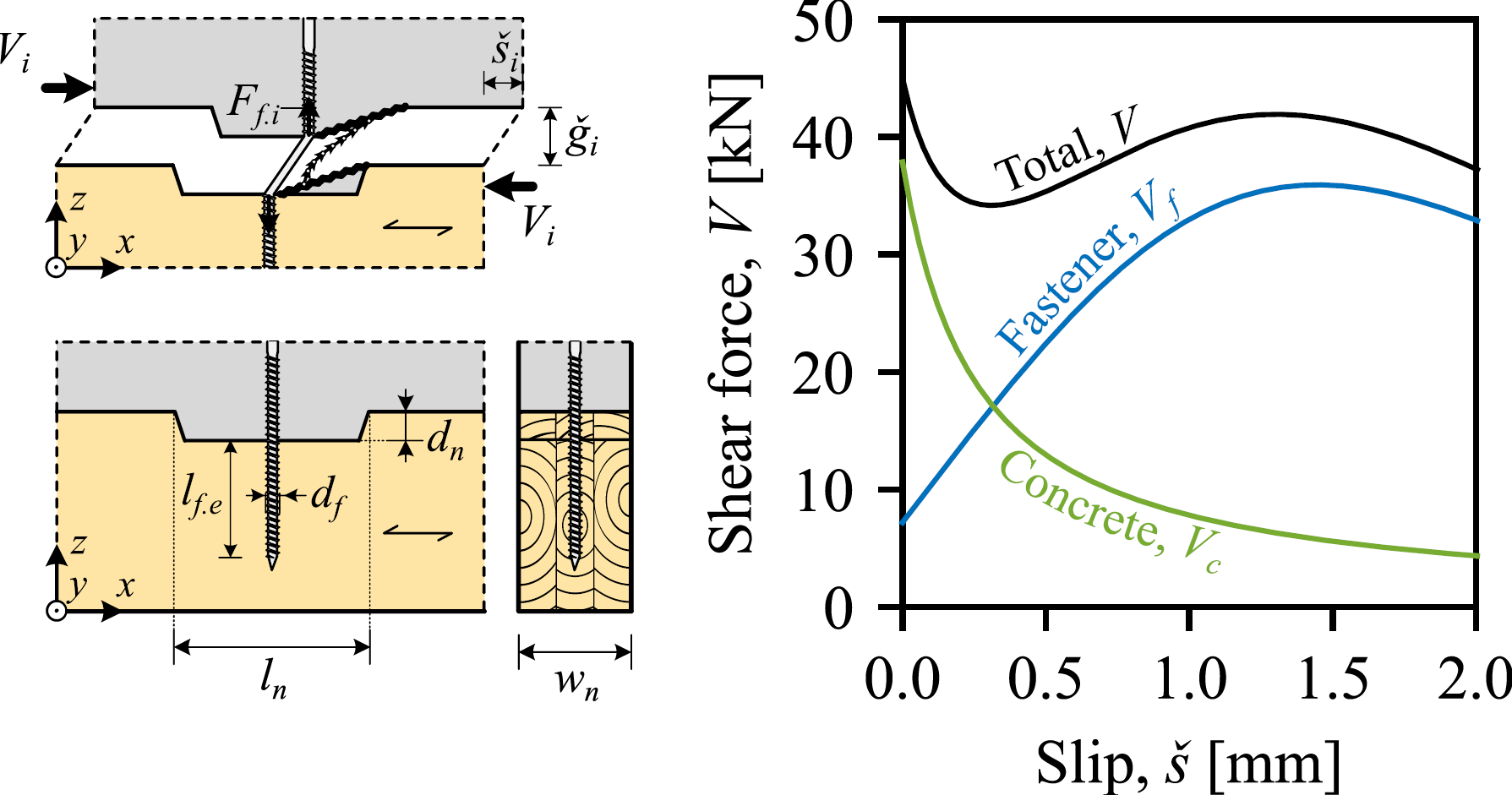
Peter Kolt Rasmussen (Technical University of Denmark/Ramboll [Industrial PhD Student]; Mitautoren: Linh Cao Hoang, Jesper Harrild Sørensen und Bent Feddersen) stellte ein mechanisch konsistentes Modell vor, das das lokale Betonversagen von Holz-Beton-Verbunddecken mit Schubnocken abbildet. Basierend auf dem fortschreitenden Verformungszustand berücksichtigt das Modell die allmähliche Entfestigung des Betons sowie die zunehmende Aktivierung der Schrauben (siehe Abbildung 3). Mit diesem Ansatz können die Schrauben so ausgelegt werden, dass die Schubnocken garantiert duktil versagen, wodurch bestehende Beschränkungen aufgehoben werden und die Verwendung von Beton mit geringerer Festigkeit (und geringerem Zementgehalt) möglich wird.

Dr. Akio Kasuga (The University of Tokyo / Sumitomo Mitsui Construction; keynote speaker) gab eine beeindruckende Präsentation über verschiedene Projekte mit Ultra-Hochleistungs-Beton, in die er in den letzten 30 Jahren als Ingenieur involviert war. Er hat bereits um 1990 kleine Brücken mit vorgespannter, nicht-metallischer Bewehrung (Aramid) realisiert – wahre Pionierarbeit. Ebenfalls beeindruckt war ich von der Entwicklung der «Schmetterlingsstege» mit hochfestem Beton und vorgespannter nicht-metallischer Bewehrung (siehe Abbildung 4). Die erste Autobahnbrücke ohne metallische Bewehrung mit diesen Stegen wurde 2020 fertiggestellt.
Diese Projekte werde ich mit Sicherheit weiterverfolgen. Ich bin gespannt auf die Resultate und die Artikel, die aus diesen Projekten entstehen. Meine Auswahl ist nicht repräsentativ, sondern entspricht einzig meinen eigenen Präferenzen. Es gab eine Vielzahl von weiteren interessanten Projekten an der Konferenz.
Teil 2 – Soziale Aspekte
Abgesehen vom Fachlichen, habe ich die folgenden Aspekte mitgenommen von der Konferenz in Budapest:
Die Diskussionen nach den Präsentationen waren meistens sehr konstruktiv und angenehm. Dies habe ich sehr geschätzt. Man hat gemerkt, dass die Zuhörer:innen beispielsweise verstehen, was es bedeutet in der Versuchshalle zu stehen und Versuche durchzuführen. Dementsprechend waren die Inputs immer sehr wohlwollend. In den Pausen kam man leicht in ein Gespräch mit anderen Teilnehmer:innen. Es fühlte sich ein wenig an, wie in der allerersten Woche im Studium.
Ich habe sehr freundliche und brilliante Forscher:innen kennengelernt mit denen ich in Kontakt bleiben werde. Die Diskussionen starteten meist beim Forschungsthema, gingen dann weiter zu allgemeineren Themen, wie den Anstellungsverhältnissen an den Universitäten oder der Arbeitskultur in der Bauindustrie in den verschiedenen Ländern, und endeten bei privaten Themen. Ich habe den Austausch ungemein geschätzt.
Erwähnen möchte ich auch noch, dass es richtig cool war, mit Fabian Morger und Rebecca Ammann (beide von der kfmResearch Gruppe) eine Woche in Budapest zu verbringen. Die Anwesenheit von Walter Kaufmann an der Konferenz haben wir auch sehr geschätzt.
Teil 3 – Fazit
Mein Fazit fällt sehr positive aus. Mein Forschungshorizont hat sich durch die Konferenz erweitert und ich kam sehr motiviert zurück nach Zürich. Ich kann nur empfehlen, das fib PhD Symposium 2026 in Wien zu besuchen.
(Tipp: Wenn man früh bucht, kann man – umweltschonend und komfortabel – mit dem Zug in der 1. Klasse für unter 100 Euro von Zürich nach Wien reisen.)

Simon Karrer
Link to English version: Gaining Insights into a Mechanical Model with Decision Trees
In diesem Blogbeitrag möchte ich zeigen, wie ich Entscheidungsbäume genutzt habe, um Einblick in ein bestehendes Modell zu gewinnen.
Dieser Blog enthält bereits mehrere Beiträge zu Anwendungen der künstlichen Intelligenz (KI) und, spezifischer, des maschinellen Lernens (ML) im Bauingenieurwesen (KI-gestützte Tragwerksplanung, KI-gestützte Fachwerkmodellgenerierung, eine Kombination aus ML und Finiten-Elemente-Analyse und die Nutzung von neuronalen Netzen in der direkten Steifigkeitsmethode). Dieser Beitrag stellt eine vergleichsweise einfache Anwendung vor, die sich an Lesende ohne vorgängige Erfahrung im maschinellen Lernen richtet.
Einer der Hauptvorteile der Entscheidungsbäume ist, dass sie auch ohne viel Erfahrung im Programmieren und ohne Vorwissen zum maschinellen Lerne relativ einfach zu implementieren sind. Dadurch sind sie besonders gut als Einstieg ins maschinelle Lernen geeignet. Gleichzeitig sind die Resultate einfach zu interpretieren, da sie als intuitiv verständliches Baumdiagramm dargestellt werden können. In diesem Beitrag benutze ich diese Eigenschaft der Entscheidungsbäume um ein bestehendes Modell besser zu verstehen, im Anwendungsbeispiel ein mechanisches Modell, das die Tragfähigkeit eines zweifeldrigen Plattenstreifens aus Stahlbeton berechnet.
Hintergrundwissen
Das maschinelle Lernen, ein Teilgebiet der künstlichen Intelligenz, umfasst verschiedene Methoden zur Beschreibung und zum Lernen aus grossen Datenmengen. Um ihrem größten Nachteil entgegenzuwirken, nämlich, dass man nicht nachvollziehen kann, wie und warum der ML-Algorithmus zu einem bestimmten Ergebnis kommt (Black-Box-Modell), wird seit kurzem im Bereich der Ingenieurwissenschaften die erklärbare KI erforscht. Bei erklärbaren KI-Algorithmen können Vorhersagen auf ihre Plausibilität und Genauigkeit hin beurteilt oder sogar mit Fachwissen nachvollzogen werden. Eine umfassende Übersicht über erklärbare KI findet sich in diesem Open-Source Paper.
Einer der einfachsten und am besten erklärbaren Algorithmen im maschinellen Lernen ist der (Klassifizierungs-)Entscheidungsbaum. Der Entscheidungsbaum lernt einen Wert (oft die Klasse “ja” oder “nein”) vorherzusagen, indem er die Eingabedaten auf der Grundlage bestimmter Eingabeparameter (der Merkmale) sukzessive aufteilt.
Der Entscheidungsprozess kann als Baum dargestellt werden, der sich bei jeder Aufteilung verzweigt. Da jeder Aufteilungsschritt durch Benutzende bewertet werden kann, ist das Ergebnis des Modells sehr gut erklärbar. Abbildung 1 zeigt das Beispiel eines Entscheidungsbaums, der Zahlen in die Klassen “Primzahl > 10” und “keine Primzahl > 10” einteilt, wobei die Merkmale «Wert» und «Anzahl Teiler» jeder Zahl im Datensatz zur Verfügung stehen. Beim Training mit dem Datensatz auf der linken Seite in Abbildung 1 sucht der Algorithmus die beste Aufteilung. Der trainierte Entscheidungsbaum (rechte Seite in Abbildung 1) kann dann genutzt werden um die Klasse von neuen Datenpunkten vorherzusagen. Das Jupyter Notebook mit dem Code dieses Beispiels befindet sich in diesem Github-Repository.
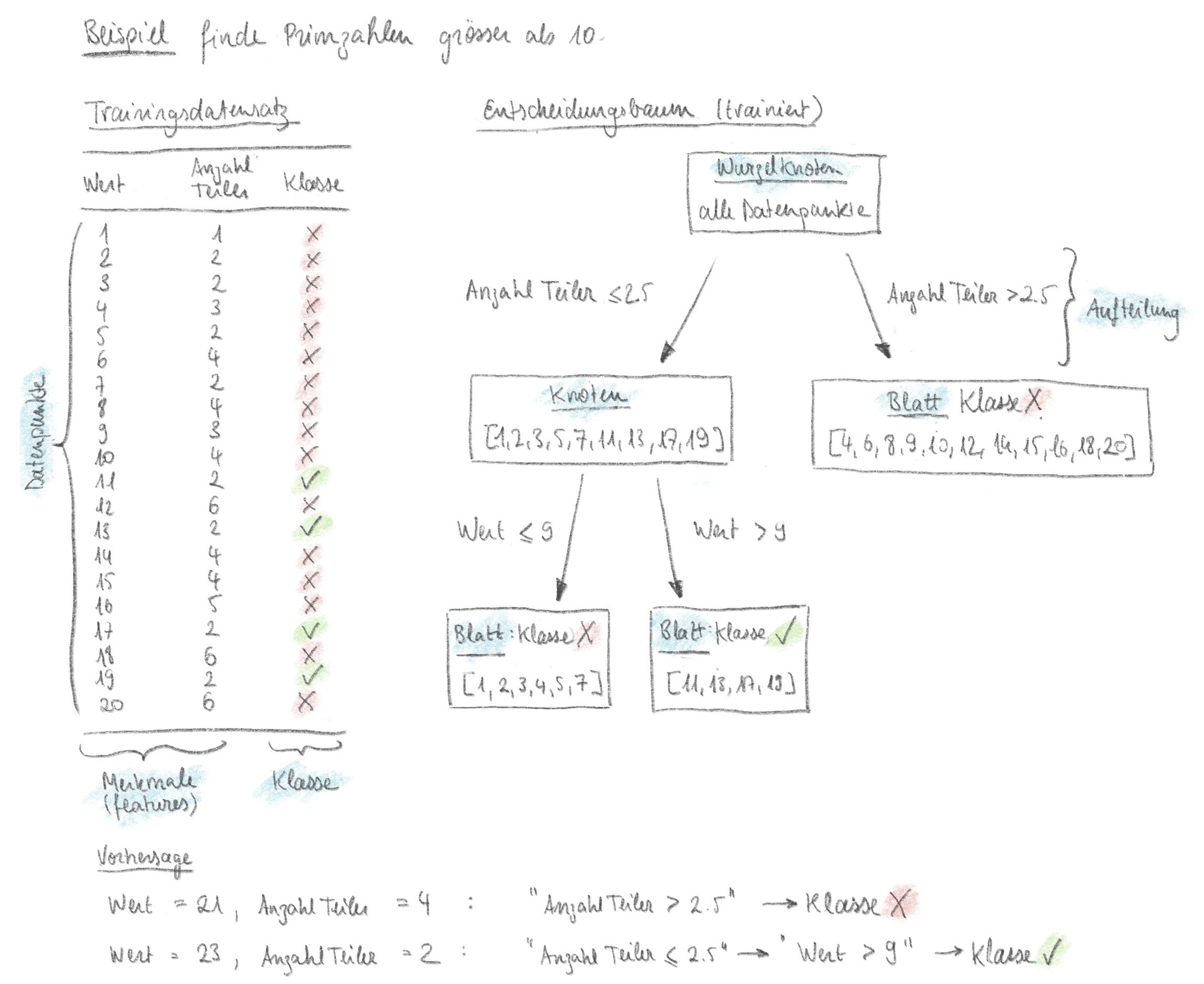
Anwendungsbeispiel
Das folgende Beispiel zeigt, wie ein Entscheidungsbaum verwendet werden kann, um Einblick in ein bestehendes mechanisches Modell zu erhalten. Der Schwerpunkt liegt nicht, wie üblich und im vorigen einfachen Beispiel gezeigt, auf der Suche nach dem genauesten Klassifizierungsmodell zur Vorhersage der Klasse neuer Daten, sondern darauf zu verstehen, mit welchen Aufteilungen der Entscheidungsbaum zum Ergebnis gelangt. Dies kann helfen zu verstehen, welche Parameter für das Ergebnis des mechanischen Modells am wichtigsten sind.
Im Anwendungsbeispiel wird ein bestehendes mechanisches Modell für einen zweifeldrigen Plattenstreifen aus Stahlbeton (Abbildung 2) verwendet. Das mit Grossversuchen validierte mechanische Modell berechnet die nichtlineare Reaktion des Plattenstreifens und kann seine Tragfähigkeit vorhersagen, wobei das begrenzte Verformungsvermögen der verwendeten Materialien berücksichtigt wird. Es ist von Interesse, welche Parameterkombinationen zu einer Tragfähigkeit führen, die grösser als die nach der Plastizitätstheorie berechnete Traglast ist1Es ist möglich mit dem mechanischen Modell Tragfähigkeiten (als Last bei Versagen) höher als die plastische Traglast zu finden, da das mechanische Modell die Verfestigung der Bewehrung berücksichtigt, während die Traglast nach Plastizitätstheorie mit der Fliessgrenze des Stahls berechnet wird.. Das bedeutet, dass die verwendeten Materialien in dieser Konfiguration ein ausreichend großes Verformungsvermögen haben, um vereinfachte Berechnungsmethoden nach der Plastizitätstheorie sicher anwenden zu können. Mehr Hintergrundinformationen dazu sind zum Beispiel in diesem Blogbeitrag.
Der Entscheidungsbaum wird so trainiert, dass er die Klasse “ok” vorhersagt, wenn die mit dem nichtlinearen mechanischen Modell berechnete Tragfähigkeit die plastische Traglast überschreitet (Qu/Qpl > 1), und andernfalls “not ok”.

Erstellung des Datensatzes
Indem das mechanische Modell viele Male mit verschiedenen Eingabewerten ausgeführt wird, kann ein Datensatz erzeugt werden. Die Wahl der richtigen Merkmale, ist einer der wichtigsten Schritte bei der Datenerzeugung. Der Datensatz könnte wie folgt aussehen:
| fs [MPa] | k [-] | εsu [-] | c [-] | ρs [%] | L [m] | fc [MPa] | Klasse |
|---|---|---|---|---|---|---|---|
| 496 | 1.09 | 0.087 | 0.11 | 0.78 | 4.37 | 54.1 | ok |
| 505 | 1.13 | 0.026 | 0.06 | 2.94 | 4.53 | 41.7 | not ok |
| 483 | 1.13 | 0.092 | 0.25 | 0.51 | 7.12 | 36.4 | ok |
| 517 | 1.07 | 0.082 | 0.08 | 0.88 | 4.37 | 57.8 | ok |
| 491 | 1.11 | 0.081 | 0.18 | 1.74 | 6.61 | 29.0 | not ok |
| … | … | … | … | … | … | … | … |
Bezeichnungen
fs: Fliessgrenze der Bewehrung
k: Verfestigungsmodul der Bewehrung (k = fs/ft, wobei ft = Zugfestigkeit der Bewehrung)
εsu: Dehnung der Bewehrung bei Erreichen der Zugfestigkeit
c: “Ausrundung” des Materialgesetzes der Bewehrung , siehe Parameter c3 in “S. Haefliger, K. Thoma, and W. Kaufmann, ‘Influence of a triaxial stress state on the load-deformation behaviour of axisymmetrically corroded reinforcing bars’, Construction and Building Materials, vol. 407 (Link)
ρs: Bewehrungsgehalt beim Zwischenauflager (der Bewehrungsgehalt im Feld wird entsprechend der elastischen Biegemomentenlinie berechnet)
L: Spannweite
fc: Druckfestigkeit des Beton
Es sollte darauf geachtet werden, das Problem so zu formulieren, dass die Klassen ausgewogen sind, d. h. dass es eine annähernd gleiche Anzahl von Daten pro Klasse gibt, da der Algorithmus sonst dazu neigt, die grösseren Klassen zu bevorzugen.
Erstellen des Entscheidungsbaums
Der Entscheidungsbaum kann zum Beispiel mit einer Implementierung aus der Open-Source Python Bibliothek scikit-learn erstellt werden. Wichtige Parameter (im maschinellen Lernen Hyperparameter genannt) sind die maximale Tiefe des Baums und die Mindestanzahl von Datenpunkten pro Split (Zwischenknoten) oder pro Blatt (Endknoten). Diese Hyperparameter helfen eine Überanpassung (Overfitting) der Daten zu verhindern, wie später erläutert wird.
Training
Der Trainingsprozess beginnt mit dem Wurzelknoten, der den gesamten Datensatz enthält. Die Daten werden dann z. B. anhand des Gini-Unreinheitskriteriums aufgeteilt. Für verschiedene mögliche Merkmale und Teilungswerte berechnet der Algorithmus die Gini-Unreinheit, um die Teilung zu finden, die die Unreinheit am besten minimiert. Anders ausgedrückt werden das Merkmal und der Wert ermittelt, die die Daten am besten in reine Teilmengen aufteilen. Der Algorithmus erstellt so eine neue Ebene mit Knoten und wechselt zu dieser.
Dieser Vorgang wird so lange wiederholt, bis die maximale Baumtiefe erreicht ist oder die Anzahl der Datenpunkte in einem Knoten zu gering ist, um eine weitere Aufteilung vorzunehmen (d. h. die Mindestanzahl der Werte pro Blatt ist erreicht). Die Genauigkeit des Entscheidungsbaums wird dann bewertet, um sicherzustellen, dass die Vorhersagen genau genug für die Interpretation sind. Dieser Artikel gibt einen Überblick über die Methoden zur Bewertung von Entscheidungsbäumen.
Interpretation der Resultate
Am einfachsten lassen sich die Ergebnisse mit Hilfe einer grafischen Darstellung des Baums interpretieren, wie z. B. mit der in scikit-learn enthaltenen Funktion oder mit dtreeviz. Dies ist natürlich nur bis zu einer bestimmten Baumtiefe möglich, danach wird es unhandlich. Abbildung 3 zeigt ein Beispiel für einen Baum mit Tiefe 3, wobei für dieses Anwendungsbeispiel auch Entscheidungsbäume mit unterschiedlichen Hyperparametern, die auf demselben Datensatz trainiert wurden, analysiert wurden.
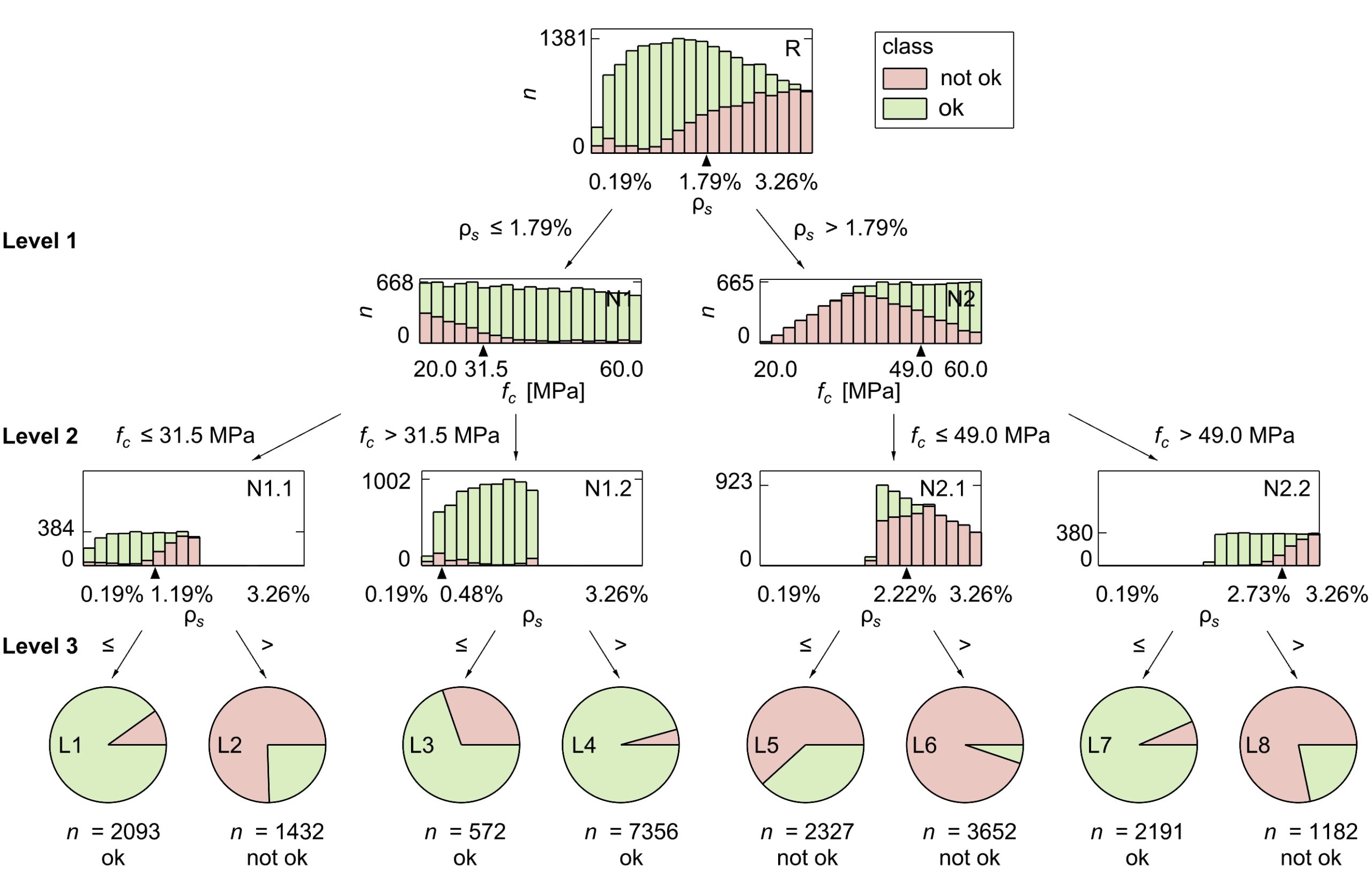
Die Aufteilungen im resultierenden Baum können mit Fachwissen interpretiert werden. Im Anwendungsbeispiel ist die erste Aufteilung immer (d. h. für alle analysierten Baumtiefen) bei einem Bewehrungsgehalt von etwa 1,8 % (siehe Abbildung 3, Level 1). Dies deutet auf einen aussagekräftigen Zusammenhang innerhalb der Daten hin.
Dieser Zusammenhang kann mit Hintergrundinformationen zu den Versagenskriterien in jedem Schnitt des mechanischen Modells interpretiert werden. Der Querschnitt kann entweder durch Bruch der Bewehrung versagen oder wenn der Beton in der Druckzone eine festgelegte Dehnung erreicht, die ein Versagen durch Betonbruch anzeigt. In Anlehnung an die grafische Darstellung, in diesem Blogbeitrag, wird deutlich, dass der Algorithmus die Daten nach der Versagensart trennt, siehe Abbildung 4. Dies ist bemerkenswert, wenn man bedenkt, dass die Daten keine Informationen über die Versagensart enthalten (siehe Tabelle 1) und spricht für deren Bedeutung im mechanischen Modell.
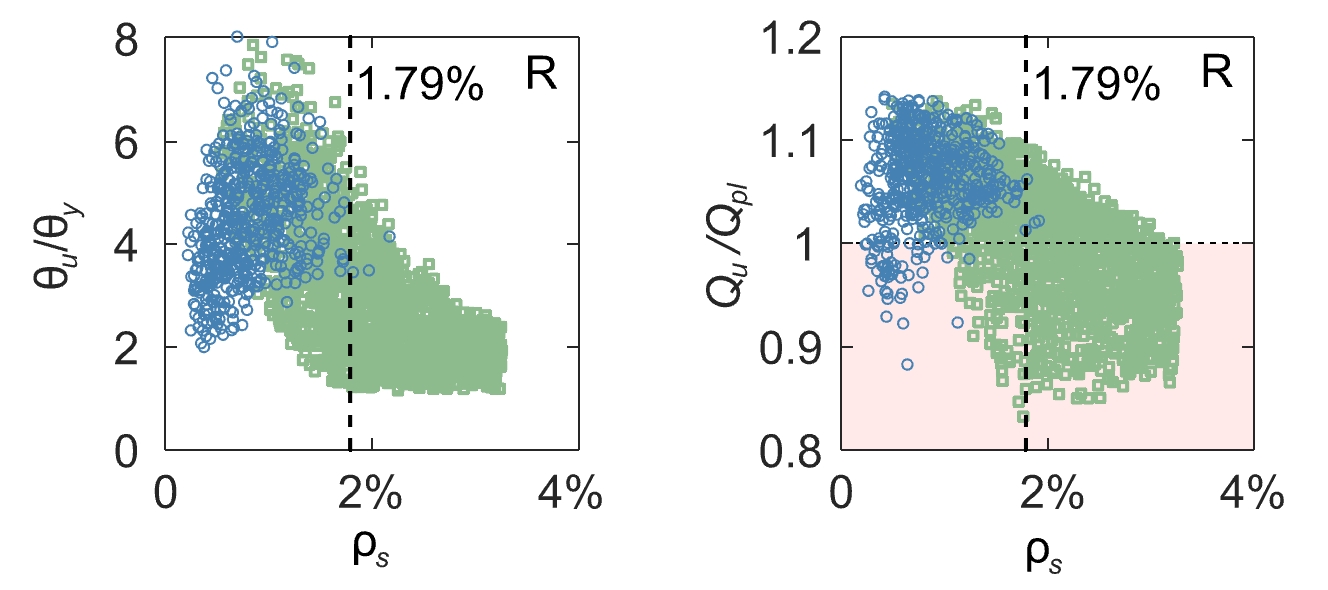
Die zweite Ebene der Unterteilungen (Abbildung 3) ist etwas weniger intuitiv, da keines der Versagenskriterien direkt von der Betondruckfestigkeit fc abhängt2Versagen durch Reissen der Bewehrung falls die Dehnung der Bewehrung in einem Schnitt grösser ist als die Bruchdehnung εsu. Versagen durch Betonbruch falls die mittlere Betondehnung am Rand des Querschnitts 5‰ überschreitet, unabhängig von der Betondruckfestigkeit.. Wenn man die Daten mit dem mechanischen Bewehrungsgrad ω auf der Abszisse aufträgt, ergibt sich ein klareres Bild. Die Betondruckfestigkeit ist Teil der Definition des mechanischen Bewehrungsgehaltes.
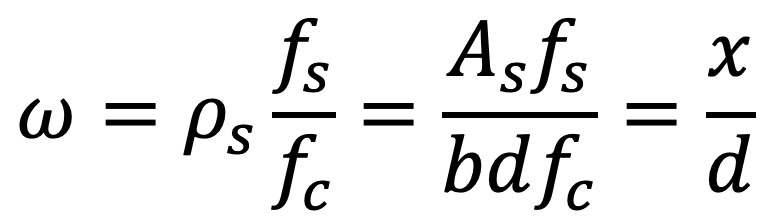
Notationen
ω: mechanischer Bewehrungsgehalt
ρs: Bewehrungsgehalt
fs: Fliessgrenze der Bewehrung
fc: Betondruckfestigkeit
As: Querschnittsfläche der Bewehrung
b: Querschnittsbreite
d: statische Höhe
x: Distanz zur neutralen Achse / Höhe der Betondruckzone
Es ist bekannt, dass dieses Verhältnis einen erheblichen Einfluss auf die Duktilität von Bauwerken hat. Es ist in den schweizerischen und europäischen Normen mit der Bedingung x/d < 0.35 enthalten, die erfüllt sein muss, um plastische Methoden bei der Bemessung anwenden zu dürfen. Interpretiert man die Aufteilung auf Ebene 2 des Entscheidungsbaums aus mechanischer Sicht, so verringert eine hohe Betondruckfestigkeit die Druckzonenhöhe x, was Reissen der Bewehrung als Versagensmechanismus und große Rotationen beim Versagen θu (d.h. hohe Duktilität) begünstigt.
Eine hohe Betondruckfestigkeit fc hält das Verhältnis niedrig, und je höher der Bewehrungsgehalt ρs, desto höher muss fc sein, um dem entgegenzuwirken. Dies könnte die unterschiedlichen Aufteilungswerte fc = 31.5 MPa und fc = 49.0 MPa an den Abzweigungen der Stufe 2 erklären, siehe Abbildung 3 und Abbildung 5.
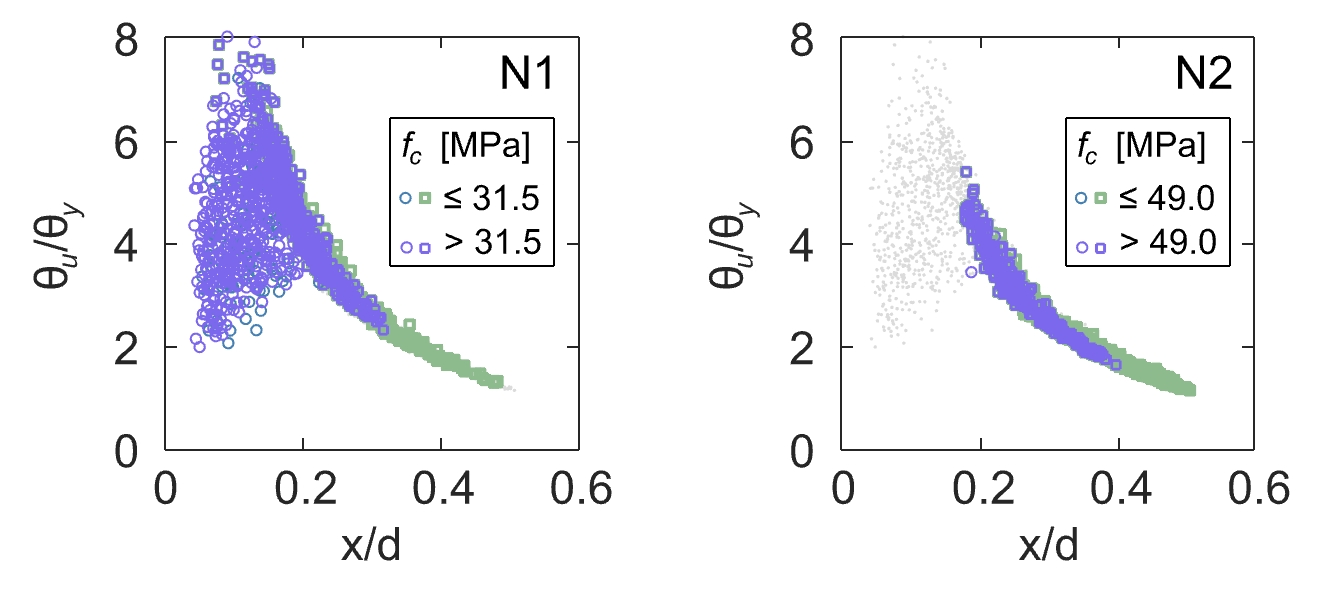
Auf Ebene 3 (siehe Abbildung 3 und Abbildung 6) sind die Daten wieder entlang des Bewehrungsgehalts ρs aufgeteilt, was die Annahme bestätigt, dass dies eine der wichtigsten Bemessungsvariablen ist. Es ist jedoch nicht üblich, dass alle Knoten auf der gleichen Ebene entlang der gleichen Variablen aufgeteilt sind. Bei der Interpretation ist es auch wichtig zu berücksichtigen, wie genau das Modell die Daten aufteilen kann. Bei der Vorhersage der Daten in Blatt L5 liegt der Entscheidungsbaum bei fast 40% des Trainingsdatensatzes falsch, siehe Abbildung 3. Aus der Aufteilung in Knoten N2.1 folgt also, dass die Klasse bei ρs > 2.22% relativ sicher «not ok» ist, und bei ρs < 2.22% eine weitere Baumebene helfen würde die Daten treffender aufzuteilen.
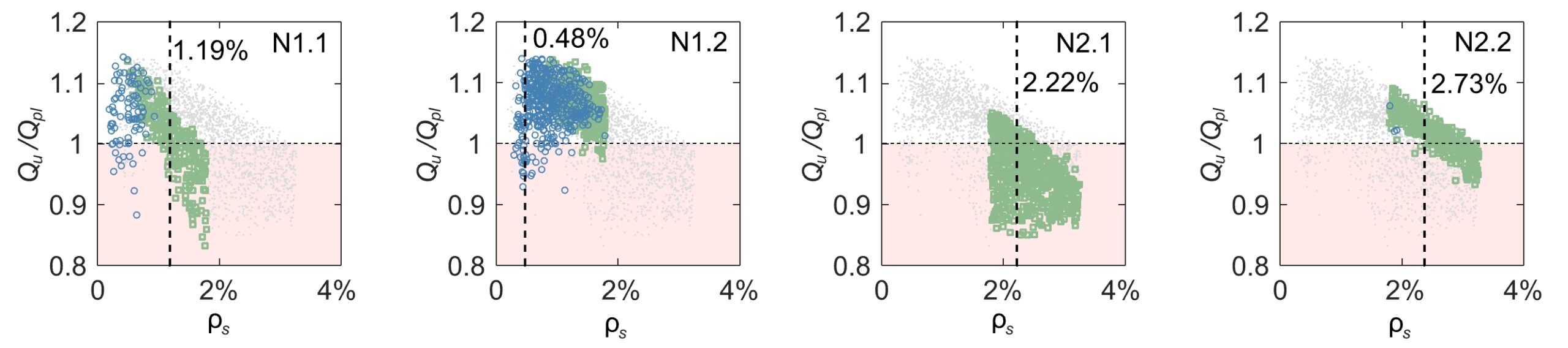
Zusammenfassend hat die Analyse der verschiedenen Aufteilungen im Entscheidungsbaum (i) dazu beigetragen, einen Einblick in die wichtigsten Merkmale zu gewinnen, und (ii) einen Anreiz geschaffen, die Beziehung zwischen diesen Merkmalen und bekannten mechanischen Prinzipien aufzudecken.
Anwendungsgrenzen
Wie bereits erwähnt, sind die Ergebnisse nur bis zu einer bestimmten Baumtiefe leicht interpretierbar, was die Anwendbarkeit für sehr komplexe Probleme einschränkt. Der Ansatz ist nur für (eine) kategorische Frage mit wenigen Antworten einfach, wie im Anwendungsbeispiel zu sehen. Darüber hinaus kann die Tatsache, dass der Entscheidungsbaum den Datensatz je Knoten nur entlang eines Merkmales aufteilen kann (siehe Abbildung 7 für eine Illustration in 2 Dimensionen), seine Anwendung auf komplexe, nichtlineare Probleme mit vielen abhängigen Merkmalen einschränken.
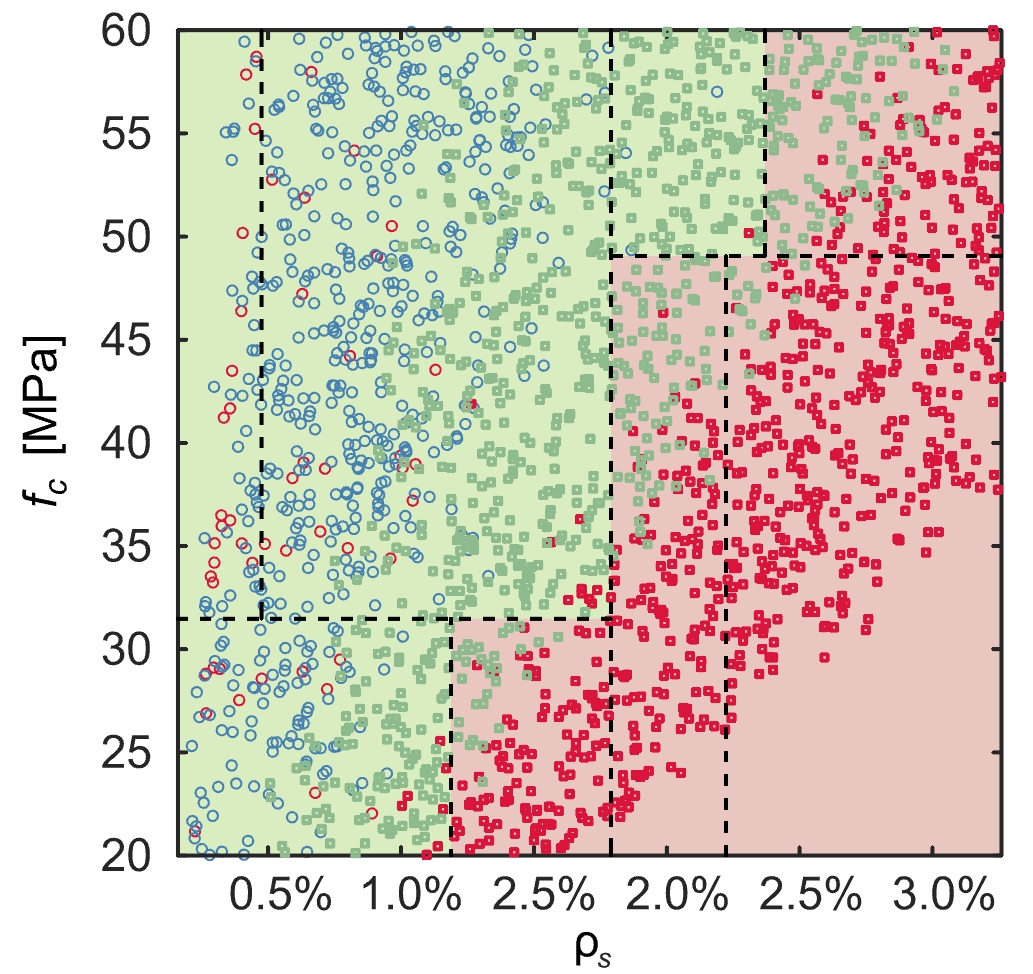
Wenn die maximale Baumtiefe zu hoch oder die Mindestanzahl von Datenpunkten pro Blatt zu niedrig angesetzt ist, kann der Entscheidungsbaum überangepasst werden und einzelne Punkte herausfiltern. Dadurch wird der angepasste Entscheidungsbaum weniger verallgemeinerbar und die physikalische Interpretierbarkeit wird untergraben. Dies kann überprüft werden, indem der Datensatz in einen Trainingsdatensatz und einen Testdatensatz aufgeteilt wird. Der Entscheidungsbaum wird mit dem Trainingsdatensatz trainiert, ohne je den Testdatensatz zu sehen. Falls der trainierte Entscheidungsbaum am Testdatensatz bedeutende weniger zuverlässige Vorhersagen liefert als am Trainingsdatensatz ist es wahrscheinlich, dass er überangepasst ist. Dieser Artikel gibt eine Übersicht über Methoden, um Überanpassung zu vermeiden oder abzumindern.
Entscheidungsbäume sind auf einen ausgewogenen Datensatz angewiesen (d.h. mit einer ähnlichen Anzahl Datenpunkte pro Klasse), da sie sonst tendenziell die stärker vertretene Klasse bevorzugen. Dieses Problem kann durch die Einführung von Gewichtungsfaktoren entschärft werden, die allerdings ihr eigenes Problem mit sich bringen, da sie Ausreissern eine übermässige Bedeutung zuschreiben. Falls der Gewichtungsfaktor der weniger vertretenden Klasse fünfmal grösser ist als der der stärker vertretenen Klasse, kann der Entscheidungsbaum ein Blatt mit einem Ausreisser der weniger vertretenen Klasse und vier gültigen Datenpunkten der stärker vertreten Klasse erstellen und dort die weniger vertretene Klasse vorhersagen. Dies ist nur durch eine genaue Plausibilitätskontrolle aller Aufteilungen im Baum bemerkbar. Es ist daher vorzuziehen, ausgewogene Datensätze zu erstellen oder, wenn möglich, vor dem Training des Entscheidungsbaums Ausreisser zu entfernen.
Wie bei allen ML-Modellen hängt das Ergebnis von Entscheidungsbäumen stark von den Daten ab. Man sollte sich bewusst sein, dass kleine Änderungen in den Daten oder auch der Hyperparameter zu einem anderen Entscheidungsbaum führen können. Da Entscheidungsbäume schnell trainiert werden können, empfiehlt es sich, die Hyperparameter zu variieren und zu prüfen, ob die Bäume und ihre Interpretation ähnlich bleiben.
Falls der Entscheidungsbaum nicht genau genug ist, kann man stattdessen ein Random-Forest-Algorithmus nutzen, der während des Trainings mehrere Entscheidungsbäume erzeugt und die Mehrheitsentscheidung dieser Bäume für einen bestimmten Datensatz und bestimmte Hyperparameter liefert. Der Algorithmus kann komplexe Datensätze besser darstellen und ist robuster gegen Überanpassung (siehe diesen Artikel für einen Vergleich). Dies geht jedoch auf Kosten der Erklärbarkeit, da die große Anzahl der generierten Entscheidungsbäume es unpraktisch macht, sie alle manuell zu interpretieren. Bei Random Forests ist es daher üblicher, die relative «Feature Importance» zur Interpretation heranzuziehen, siehe Abbildung 8.
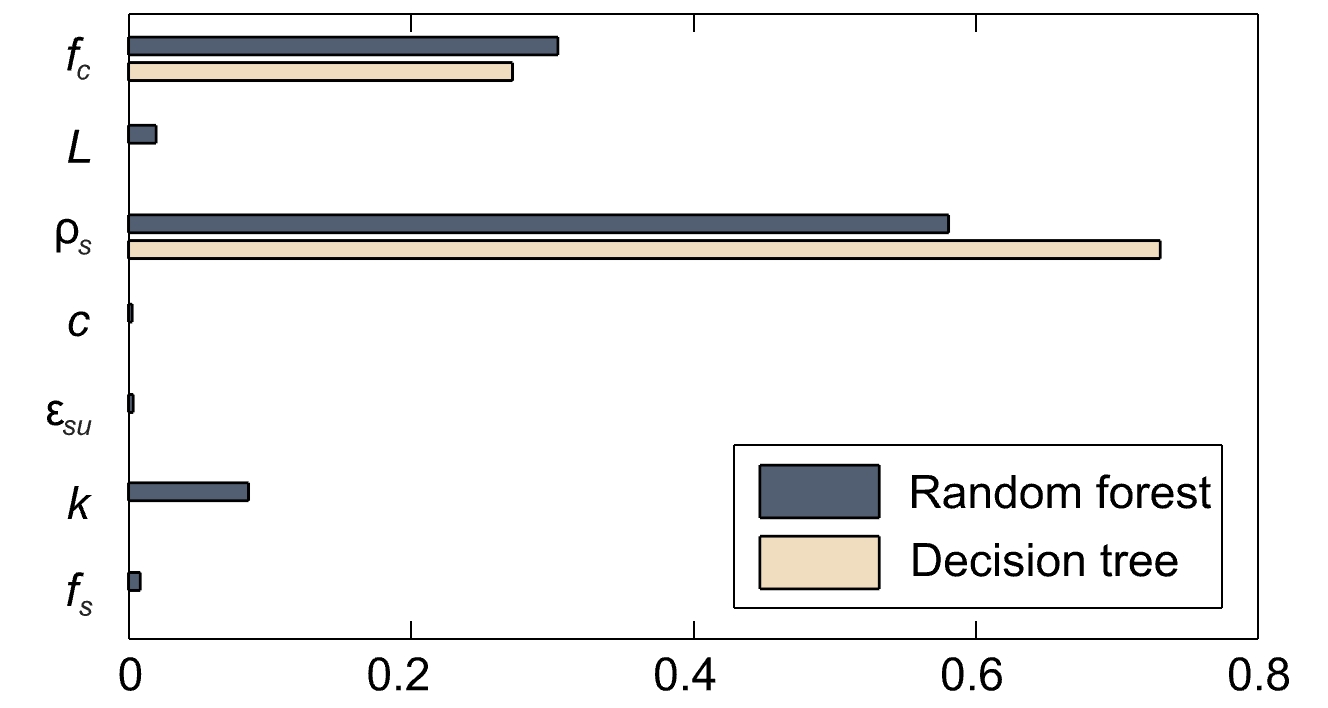
Persönliche Einschätzung
Trotz der Einschränkungen halte ich die Verwendung eines Entscheidungsbaums auf Daten, die von einem bestehenden Modell generiert wurden, für einen interessanten Ansatz, da man mit wenig Aufwand ein besseres Verständnis des Modells und der Daten erlangen kann. Der Prozess hat mir geholfen, mich nicht von der hohen Dimensionalität (viele Merkmale) des mechanischen Modells überwältigen zu lassen, da der Entscheidungsbaum einige Hinweise darauf gab, auf welche Merkmale ich mich konzentrieren sollte. Es hatte auch den Vorteil, dass es meine Kreativität anregte und mich dazu brachte, anders über das Problem nachzudenken, wenn die Ergebnisse nicht mit meinen Erwartungen übereinstimmten. Dies führte dazu, dass ich mein vorläufiges theoretisches Wissen über das Problem vertiefte und schließlich zu einem tieferen Verständnis des mechanischen Modells gelangte.
Ressourcen
Dieses Github-Repository enthält eine kurze Anleitung für den Einstieg ins maschinelle Lernen mit Entscheidungsbäumen (mithilfe der sklearn Toolbox und Visual Studio Code) und das Jupyter Notebook mit dem Code für den Entscheidungsbaum aus Abbildung 1 (Primzahlen).
Nathalie Reckinger
Link to English version: Introduction to the Deep Neural Network Direct Stiffness Method (DNN-DSM)
Dieser Blog-Beitrag beschreibt einige grundlegenden Schritte, die für die Herleitung der Deep Neural Network Direct Stiffness Method (DNN-DSM) erforderlich waren. Die konzeptionelle Methodenableitung ist im Wesentlichen in drei Teile gegliedert: (i) die Finite-Elemente-Simulation und die Entwicklung geeigneter Datensätze auf der Grundlage lokaler Schalenelement-Simulationen, die Instabilitäten auf Querschnittsebene abdecken; (ii) die Entwicklung neuronaler Netze, die zur Vorhersage einzelner inkrementeller Tangentensteifigkeiten geeignet sind; (iii) die Implementierung neuronalen Netze in die direkte Steifigkeitsmethode.
Die entwickelten DNN-Modelle wurden auf Datensätzen trainiert, die aus einem Pool numerischer (LBA und GMNIA) Schalen-FE-Simulationen abgeleitet wurden. Diese wurden so konzipiert, dass ausschliesslich lokales Beulen das Hauptinstabilitätsphänomen für die untersuchten rechteckigen und quadratischen (RHS und SHS) Querschnitte ist, siehe Abbildung 1.
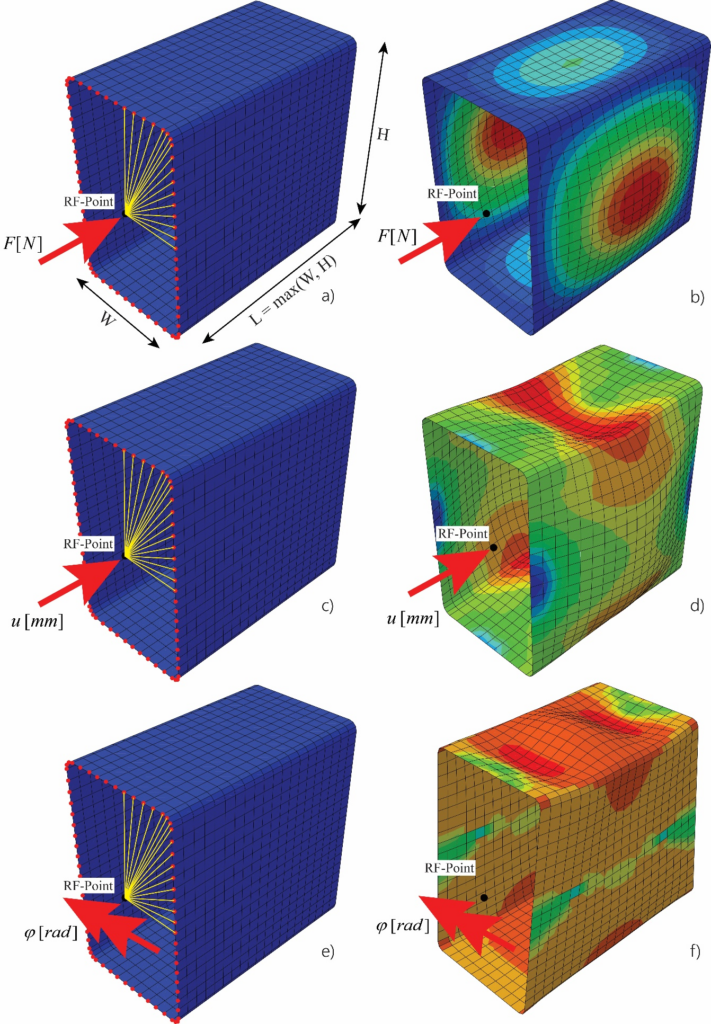
Die hauptsächliche Verifizierungsarbeit, basierend auf einer Vielzahl experimenteller und numerischer Untersuchungen, geht auf das Hollosstab-Projekt zurück (Link). Die abgeleiteten FE-Modelle wurden auf der Grundlage dieser Untersuchung teilweise angepasst und weiterentwickelt, um die Bedingungen für lokales Beulen zu erfüllen. Die entwickelten FE-Modelle werden wie folgt beschrieben: (i) Abaqus Typ S4R Elemente, mit einer Diskretisierung von etwa 60 Elementen in Umfangsrichtung und 50 – 100 Elementen pro Meter in Längsrichtung; (ii) Geometrien basieren auf den Normvorgaben von EN 10210-2:2006 und EN 10219-2: 2006, mit der Länge L als dem größeren Wert der Breite W oder der Höhe H; (iii) Verformungen, die durch definierte Bezugspunkte am oberen und unteren Rand des Querschnitts aufgebracht werden sind verbunden durch MPC-Pin-Formulierungen; (iv) Verwendung von nichtlineare Materialmodelle für warmgewalzten (bilineares + nichtlineares Modell) und kaltgeformten Stahl (zweistufiges Ramberg-Osgood-Modell); (v) LBA-Analyse zur Ermittlung des elastischen kritischen Beulwiderstands und der Eigenform (lokale Imperfektionen); (vi) GMNIA-Simulation zur Bestimmung des realistischen Knickwiderstands.
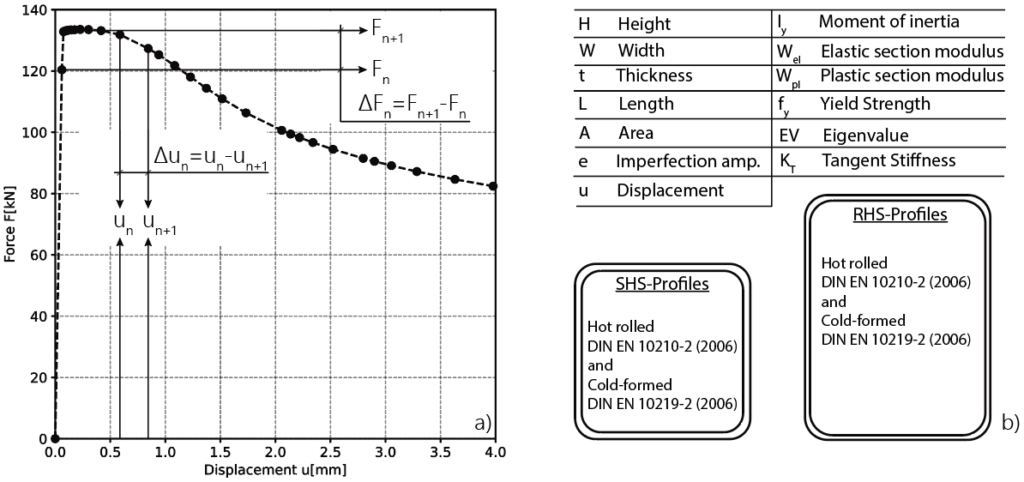
526 europäische warmgewalzte und kaltgeformte RHS- und SHS-Profile, drei verschiedene Stahlsorten von normal- bis hochfest (S355, S460 und S700), sowie drei verschiedene lokale Imperfektionsamplituden (B/200, B/300 und B/400; wobei B das kleinere Maß der Profilhöhe oder -breite ist) wurden bei der Datenerstellung berücksichtigt. Insgesamt wurden 9468 GMNIA-Simulationen durchgeführt, um die Grundlage für die anschliessende Datensatzgenerierung zu schaffen.
Hierbei wurden die LBA Ergebnisse aus Abaqus verwendet, um die querschnittsabhängige elastische kritische Beullast zu extrahieren. Die Ergebnisse der GMNIA-Analysen wurden hingegen zur Bestimmung der inkrementellen Verformungs- und Rotationsschritte und der damit verbundenen Differenzialkräfte und -momente verwendet, siehe Abbildung 2 a) beispielhaft für den Lastfall Druck. Diese Werte wurden anschließend zur Berechnung der inkrementellen Tangentensteifigkeiten herangezogen, die die Grundlage für den Trainingsoutput der DNN-Modelle bilden.
Insgesamt sind im Rahmen von Voruntersuchungen 193 Einzelkombinationen für verschiedene DNN-Modelle mit der Random Search Methode getestet worden. Dieser Arbeitsablauf ist geeignet, um die allgemeinen Tendenzen innerhalb der DNN-Architektur zu erkennen. Alle Berechnungen wurden auf der Grundlage einer Train-und-Test-Philosophie durchgeführt, d.h. eine bestimmte Datenmenge wurde für das Training (80%) und eine zusätzliche unabhängige Menge für den Validierungsprozess (20%) verwendet. Das verwendete DNN-Modell besteht aus vier Schichten (27, 27, 18 und 9 Neuronen), die jeweils mit einer ReLU-Aktivierungsfunktion enden. Während des Optimierungsprozess wurde eine Lernrate von 0,0005 sowie der Adam-Optimizer verwendet.

Die allgemeine Implementierung der DNN-DSM basiert auf der generischen Definition der direkten Steifigkeitsmethode für Balkenelemente.
![]()
Die DNN-DSM nutzt diese Implementierung zur Vorhersage einer lokalen nichtlinearen Tangentensteifigkeitsmatrix in Abhängigkeit von gegebenen Knotenverformungen oder -verdrehungen. Das neuronale Netz verwendet einige der Merkmale aus Abbildung 2 b)sowie eine absolute Verformung bzw. Verdrehung in jedem Belastungsschritt (siehe Abbildung 3 a) für Druck und b) für Biegung), um eine lokale nichtlineare Tangentensteifigkeitsmatrix vorherzusagen, wie durch die folgende Gleichung für die getrennten Fälle vorgeschlagen.
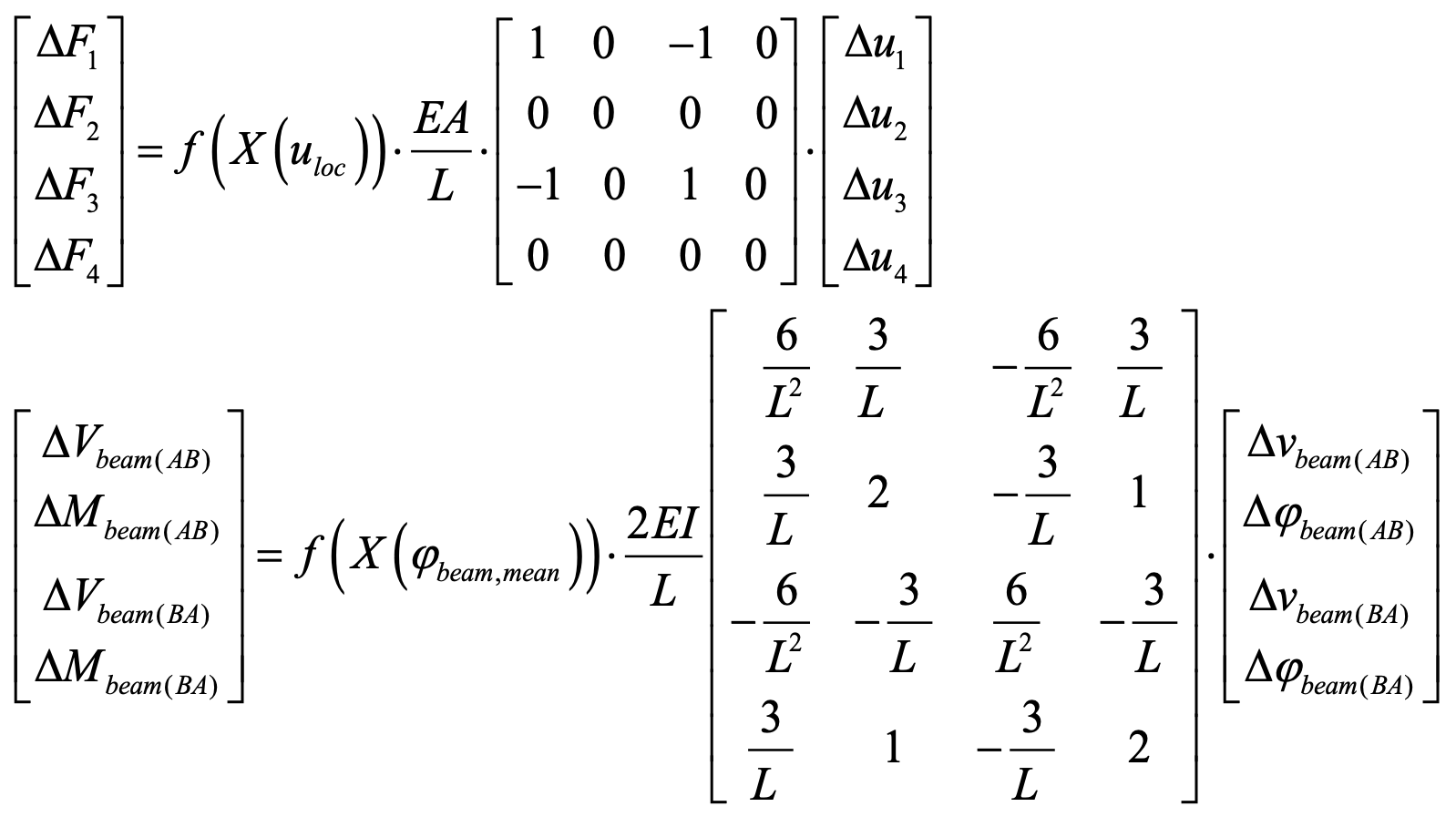
Die Implementierung des Balkenelements unterscheidet sich geringfügig von der des Fachwerkelements, indem die Balkensteifigkeitsmatrix entsprechend einer vorgegebenen mittleren Drehung φ modifiziert wird. Eine zugehörige Definition ist Abbildung 3 b) zu entnehmen. Im Rahmen der vorgestellten Methode wird eine gleiche konstante Verdrehung (in der Ebene) an beiden Enden angenommen. Dies ist unter der Annahme kleiner Elementlängen genau genug für die Approximation von Schnittkräften.
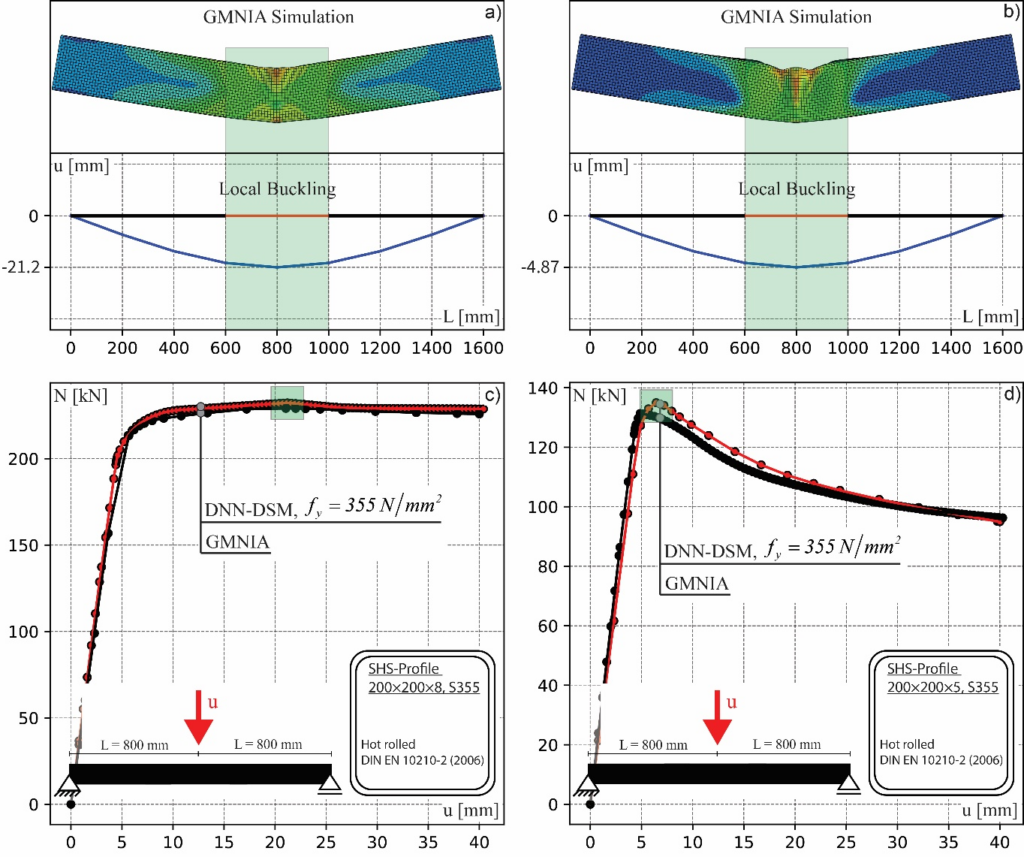
Ein exemplarischer Auszug der Ergebnisse für Dreipunktbiegung ist in Abbildung 4 für zwei warmgewalzte Profile dargestellt, ein SHS200x8 (S355) und ein SHS200x5 (S355). Weiter werden in Abbildung 4 a) und b) die Ausgangsverformungen aus Abaqus und den entsprechenden DNN-DSM-Vorhersagen dargestellt. Beide Abaqus-Modelle bilden eine lokale Beule um den bzw. im Lasteinleitungsbereich. Die DNN-DSM Modelle werden aus 8 Elemente zusammengestellt mit jeweils 2 dofs an jedem Endknoten, die die vertikale Verschiebung und Verdrehung repräsentieren. Diese Definition führt zu einer Gesamtzahl von 18 dofs für das dargestellte System. Zu beachten ist, dass das Abaqus-Modell 77298 dofs verwendet, um die nichtlinearen Last-Verformungs-Kurven aus Abbildung 4 c) und d) zu berechnen. Im Vergleich kann nun ein sehr ähnliches Ergebnis mit dem DNN-DSM-Ansatz nachgeahmt werden. Die Elemente um die Lasteinleitung herum erreichen ihre maximale querschnittsabhängige Kapazität und gehen in den Nachbeulbereich über, mit stetigem Steifigkeitsverlust und einem Gesamtabfall der Lasten. Die Abweichungen der maximalen Kräfte liegen in diesem Fall unter 3%. Für das Profil SHS200×5 liegen die Ergebnisse mit dem DNN-DSM-Ansatz 30% über den der schalenbasierten GMNIA Ergebnissen. Dies kann auf Effekte zurückgehen, die durch die DNN-DSM nicht zwangsläufig berücksichtigt werden und das Gesamtverhalten beeinflussen könnten, wie z.B. lokale Quetschungen im Bereich der Lasteinleitung oder Unterschiede in den Beullängen. Nichtsdestotrotz konnte das Gesamtsystemverhalten mit der DNN-DSM erfolgreich nachgebildet werden, wobei rechenzeitliche Vorteile gegenüber Abaqus Simulationen ersichtlich waren. Der DNN-DSM Berechnungsprozess wurde nach ca. 150 Sekunden beendet, die Abaqus-Berechnung nach ca. 240 Sekunden. Diese Zeit beinhaltet nur die eigentliche Berechnung. Die Berücksichtigung des Modellierungsaufwands zur Erstellung der LBA und GMNIA Analysen würde zu deutlich größeren Unterschieden führen.
Zusammenfassend gibt dieser Beitrag einen Einblick in die Entwicklung und Anwendung der DNN-DSM Methode, einem neuartigen Ansatz, bei dem die direkte Steifigkeitsmethode mit neuronalen Netzwerkmodellen gekoppelt wurde, um das lokale Beulverhalten schalenbasierter FE-Simulationen zu imitieren. Neben der Datenentwicklung, der Datensatzgenerierung und der Methodenimplementierung wurde ein exemplarischer Vergleich zwischen der DNN-DSM und Abaqus GMNIA Simulationen herausgearbeitet. Dieser Vergleich zeigt einerseits, dass der gesamte Last-Verformungspfad im Vor- und Nachbeulbereich reproduziert werden kann und andererseits die Möglichkeiten hinsichtlich Modellgrössenreduktion und Zeitersparnis. Falls dieser Artikel das ein oder andere Interesse geweckt hat finden sich ausführlichere Erläuterungen mit zusätzlichen Hintergrundinformationen unter der folgenden Veröffentlichung (Link, [1]).
Andreas Müller
Literatur
| [1] | Müller, A. Advanced Inelastic Analysis and Design of High Strength Steel Structures with Machine-Learning-Derived Predictive Methods. Doctoral Thesis (2023). ETH Zürich. |
Link to the English version: On the use of High-Performance Fiber Reinforced Concrete in bridge design.
Dieser Beitrag beleuchtet die Ergebnisse eines laufenden Forschungsprojekts der Universidad Politécnica de Madrid (UPM) zusammen mit dem Construction Technology Centre von ACCIONA, das die Anwendung von Hochleistungsfaserbeton (HPFRC) im Infrastrukturbau untersuchen soll. Das Projekt verfolgt einen umfassenden Ansatz, der die Entwurfsplanung, die Materialentwicklung und Versuche umfasst. Das führende UPM-Team besteht aus Rafael Ruiz, Hugo Corres und Leonardo Todisco. Leonardo ist in diesem Semester als Gastprofessor am Lehrstuhl für Massiv- und Brückenbau an der ETH Zürich tätig.
HPFRC hat eine Druckfestigkeit von etwa 100-120 MPa, was im Vergleich zu herkömmlichem Beton höhere Vorspanngrade ermöglicht. Dieses Potenzial erlaubt eine erhebliche Verringerung des Betonvolumens und fördert die Realisierung grösserer Spannweiten bei Betonfertigteilbrücken. Darüber hinaus können die Beiträge der Stahlfasern und der Vorspannung zum Schubwiderstand die herkömmliche Schubbewehrung ersetzen, die bei konventionellen Balkenbrücken etwa 40% des Bewehrungsstahls ausmacht. Die Forschungsergebnisse zeigen, dass ein Fasergehalt von etwa 80 kg/m3 (Vf ≈ 1%) ausreicht, um eine ausreichende Duktilität zu gewährleisten, wenn die Bügel entfernt werden. Darüber hinaus ermöglicht die schnelle Festigkeitsentwicklung des Betons ein frühes Vorspannen, was den Herstellungsprozess beschleunigt. Diese hohe Frühfestigkeit ist mit einer schnelleren Entwicklung der Kriechverformungen verbunden, wodurch Langzeiteffekte wie verzögerte Vorspannkraftverluste reduziert werden. Schliesslich werden diese mechanischen Eigenschaften durch eine erhebliche Verbesserung der Dauerhaftigkeit im Vergleich zu herkömmlichem Beton ergänzt.
Die entwickelte HPFRC-Mischung, die 500 kg/m3 Zement, 50 kg/m3 Silikastaub und 80 kg/m3 Stahlfasern der Länge 4d-60 mm enthält, bietet vielversprechende mechanische Eigenschaften bei Kosten, die etwa 2,5 bis 3,0 mal so hoch sind, wie die von herkömmlichem Beton, also deutlich niedriger als bei einem Ultra-Hochleistungs-Faserbeton. Der entwickelte HPFRC weist eine Druckfestigkeitsklasse C120, eine Biegefestigkeitsklasse nach Rissbildung von 13a und eine Ausbreitungsklasse F5 auf.
Der entwickelte HPFRC wurde für den Entwurf eines U-förmigen Trägers für Strassenbrücken verwendet (Link).
Der Brückenüberbau besteht aus zwei U-förmigen Trägern, die jeweils aus drei 20 Meter langen Fertigteilsegmenten bestehen, so dass sich eine Gesamtspannweite von 60 Metern ergibt. Der Brückenüberbau wird durch eine Fahrbahnplatte aus herkömmlichem Beton vervollständigt. Sein Querschnitt und ein 3D-Bild sind in Abbildung 1 dargestellt. Die Vorspannung befindet sich ausserhalb des Betons, innerhalb des U-Trägers, was zu einer starken Reduzierung der Dicke von Stegen und Bodenplatte führt. Ausserdem weichen einige Spannglieder bei L/5 von den Stützen ab, um eine bessere Annäherung an die Biegemomentenverteilung zu erreichen.
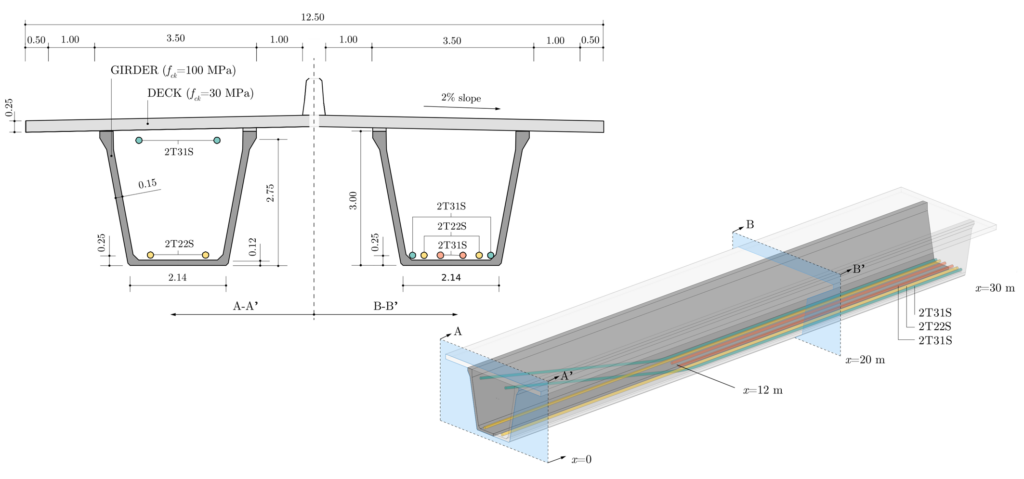
Im Vergleich zu anderen Referenzprojekten mit ähnlichen geometrischen Merkmalen und konventionellen Materialien wird der Betonverbrauch um 50% reduziert, die Bewehrung um 67% und der Spannstahl um 17%. Insgesamt führt die HPFRC-Lösung zu einer Kostenreduzierung von 14%, ungeachtet zusätzlicher Vorteile wie einem geringeren Eigengewicht und einer höheren Haltbarkeit.
Um Bedenken hinsichtlich (i) Kaltfugen zwischen den Gussstücken und (ii) der Faserorientierung auszuräumen, wurden zwei rechteckige Platten (Abbildung 2, links) in vier Schichten gegossen und mit einer Vibriernadel verdichtet. Es wurden prismatische Proben mit variabler Ausrichtung entnommen. Die Ergebnisse nach EN 14651 (Abbildung 2, rechts) wurden als zufriedenstellend eingestuft, ohne erkennbare Auswirkungen, die auf die Faserausrichtung oder Diskontinuitätsebenen zurückzuführen sind (Link).
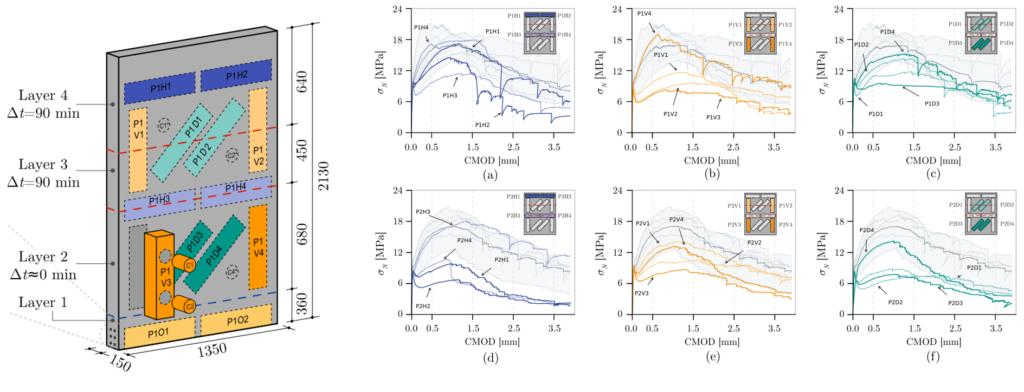
Das Schubverhalten solcher Elemente wird jedoch immer noch wissenschaftlich diskutiert und die meisten Bemessungsmodelle liefern stark streuende und sehr konservative Vorhersagen (Link), die von der Verwendung von HPFRC abhalten. Daher wurde eine experimentelle Untersuchung an acht HPFRC-Balken in Originalgrösse durchgeführt (Abbildung 3). Die Balken wurden mit unterschiedlichen Vorspanngraden getestet und die Verformungen wurden mit Digitaler Bildkorrelation (DIC) gemessen.
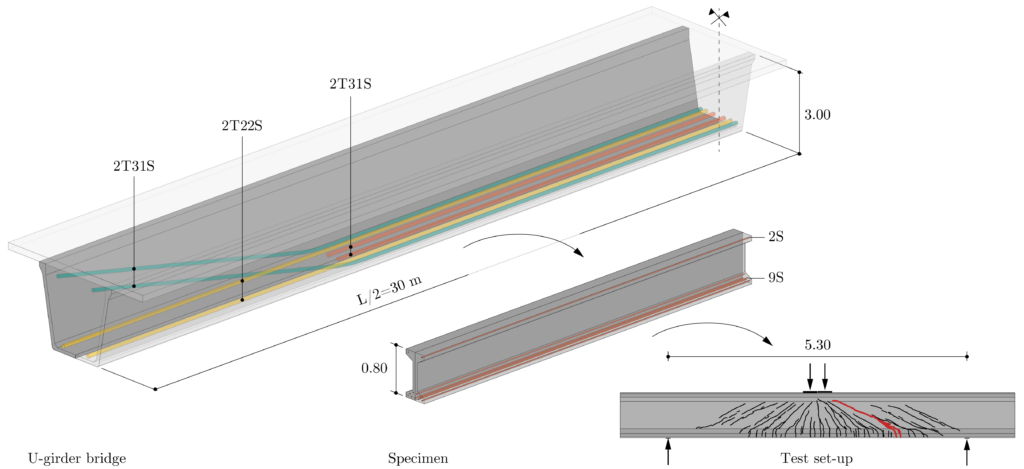
Anhand der experimentellen DIC-Daten wurden die Rissentwicklung und -Kinematik im Detail untersucht, ebenso die damit verbundenen Beiträge potenzieller Schubübertragungsvorgänge (Link). Die Ergebnisse (Abbildung 4) zeigen einen signifikanten Beitrag der Fasern sowie der Neigung des Druckgurtes bei hohen Vorspannungen, während die anderen potenziellen Schubbeiträge (d.h. Rissverzahnung, Dübelwirkung) vernachlässigbar sind.
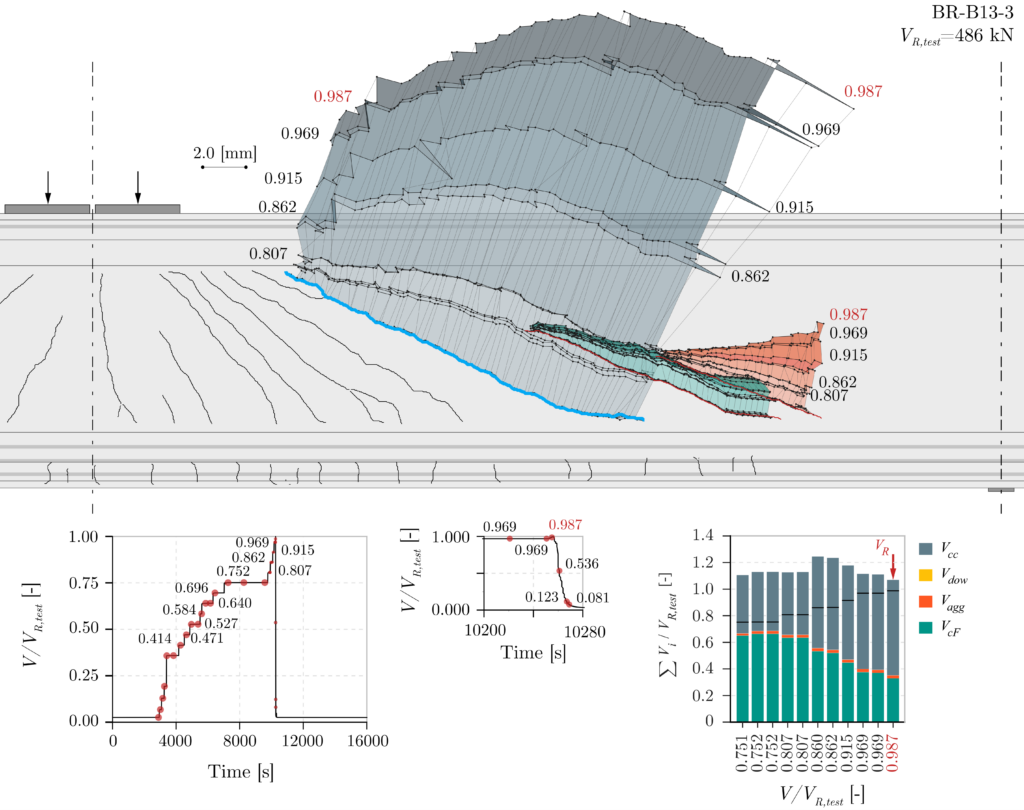
Zusammenfassend lässt sich sagen, dass die Studie wertvolle Einblicke in die Anwendung von HPFRC im Infrastrukturbau lieferte und dessen Potenzial zur Veränderung des traditionellen Brückenentwurfs hervorhob. Eine Balkenbrücke mit 60 m Spannweite aus HPFRC wurde als kostengünstige (-14%) Alternative zu konventionellen Lösungen identifiziert. Sie besteht aus drei vorgefertigten Segmenten, die durch Spannglieder ohne Verbund vorgespannt sind. Dank der Vorspannung und dem Beitrag der Fasern zum Schubwiderstand ist keine Bügelbewehrung erforderlich. Die laufenden Bemühungen konzentrieren sich auf die Verfeinerung der Modelle für die Schubbemessung, um den einzigartigen Eigenschaften von HPFRC besser Rechnung zu tragen und seine breite Einführung in der Praxis zu erleichtern.
Leonardo Todisco
Link to the English version: A novel combination of Machine Learning and the Finite Element Analysis.
Einige der letzten blog Beiträge haben sich schon der Nachhaltigkeit im Betonbau gewidmet (z.B. Blog Rebecca Ammann, Blog Sophia Kuhn). In diesem Blogpost wird eine neue Methodik vorgestellt, die effizientere Entwürfe und Überprüfungen von bestehenden Stahlbetonbauten ermöglichen soll, sodass die Verwendung von Beton reduziert werden kann und wir nachhaltiger bauen können.
Bestehende Entwurfsmethoden für Stahlbetonbauten basieren hauptsächlich auf den linear-elastischen Finite-Elemente-Analysen (LFEA). Sie approximieren das stark nichtlineare Materialverhalten von Stahlbeton mit linearen Modellen und sind deshalb teils sehr konservativ (Thoma et al. 2014). Solche Annäherungen können deshalb zu wirtschaftlich wie auch umwelttechnisch ineffizienten Designs von Stahlbetonbauten führen. Andererseits bestehen viele Modelle für nichtlineare Finite-Elemente-Analysen (NLFEA), welche unterschiedlichen methodologischen Ansätzen folgen. Ein Beispiel ist die Implementierung des mechanisch konsistenten Gerissenen Scheibenmodell (engl.: Cracked Membrane Model, Kaufmann und Marti 1998, Thoma et al. 2014). Diese Methode kann das Materialverhalten von Stahlbeton im Vergleich zur LFEA genauer abbilden und ist universell einsetzbar, auch bei diskontinuierlichen Strukturen (siehe auch füherer Blogbeitrag von Marius Weber). Dennoch werden NLFEA selten in der Praxis verwendet, da sie rechnerisch ineffizient sind und komplexe Abhängigkeiten von verschiedenen Materialparametern aufweisen. Nur selten wird mehr als eine NLFEA Berechnung ausgeführt, was es schwierig macht, unterschiedliche Lastsituationen oder Überprüfungsszenarien zu betrachten oder sogar Strukturen zu optimieren.
Neue digitale Prozesse, wie maschinelles oder tiefes Lernen (engl.: Machine and Deep Learning, ML / DL), wie auch differenzierbare Simulation sind hingegen der neuste Stand der Technik bezüglich ableitungsbasierten Optimierungsmethoden. Für ML und DL wurde zum Beispiel gezeigt, dass diese Methoden neue Muster aus Daten erkennen können und gut über Datensätze hinweg generalisieren können (LeCun et al. 2015, Shen et al. 2023). Sobald sie trainiert sind, können sie schnell gewünschte Zielparameter vorhersagen. Neue Entwicklungen in physik-basiertem maschinellem Lernen (PBML) haben gezeigt, dass die Kombination von ML mit bestehenden computergestützen physikalischen Modellen ein grosses Potenzial birgt. Dies wurde in diversen Anwendungsgebieten wie zum Beispiel Fluiddynamik, Festkörpermechanik wie auch Strukturmechanik gezeigt. Ein Beispiel von PBML sind physik-informierte neuronale Netze (PINNs, Raissi et al. 2019), bei denen im Vergleich zu konventionellen neuronalen Netzen (NN) die zugrundeliegenden physikalischen Gleichungen, z.B. Differenzialgleichungen, direkt in die Verlustterme des NNs eingefügt werden. Abbildung 1 zeigt ein Beispiel eines PINNs für einen Stahlbetonbalken mit Euler-Bernoulli Balkengleichung. Als Datensatz werden nur die Stellen x benötigt, an denen man die Differenzialgleichung auswerten möchte. Sobald das PINN trainiert ist, kann es für gegebene Geometrie, Materialparameter und Last die Verschiebungen (w) und Momente (M) eines einfach gelagerten Balkens an der gewünschten Stelle x vorhersagen.
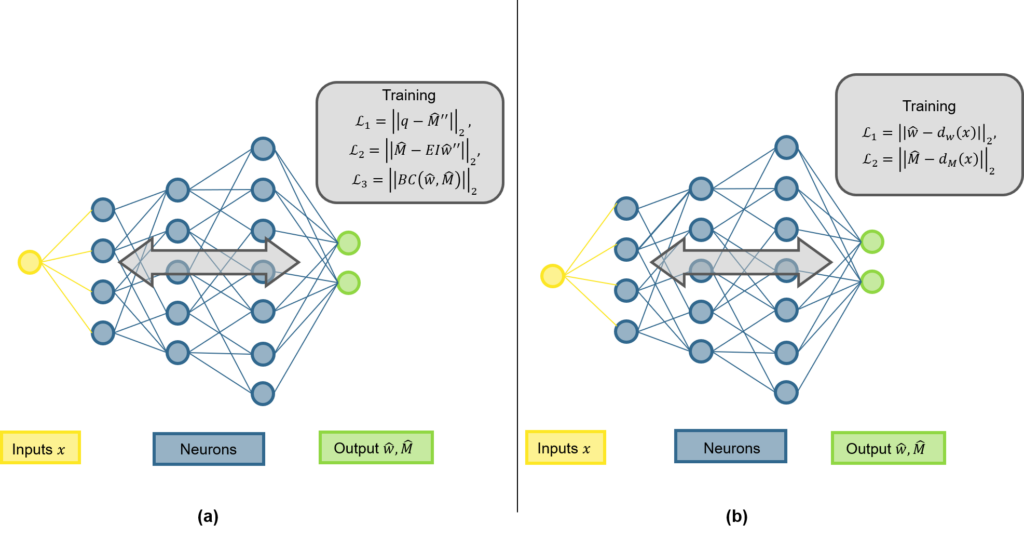
Damit man ML / DL – Methoden im Bausektor anwenden kann, ist es wichtig, grundlegende Theorien des Anwendungsgebiets (z.B. die Differenzialgleichung des Euler-Bernoulli-Balkens) miteinzubeziehen bei der Erstellung der Methode, wie es zum Beispiel bei PINNs möglich ist, sodass eine Akzeptanz wie auch Validierungsmöglichkeit geschaffen wird. Zusätzlich gibt es im Bausektor typischerweise wenig verfügbare Daten mit denen man ein ML Modell trainieren könnte, weshalb es noch wichtiger ist, physik-basierte Methoden zu verwenden. Obwohl diese Methoden gute Resultate zeigen, sind sie limitiert in ihrer Generalisierbarkeit ausserhalb des Parameterraums in dem sie trainiert wurden, was die Anwendung solcher Methoden auf reale Probleme im Betonbau äusserst einschränkt. Deshalb wollen wir eine neue Methode entwickeln, die ML mit traditionellen FEA kombiniert, wobei die Hauptanliegen in Abbildung 2 dargestellt sind: Die Methodik soll auf Bauteilebene entwickelt werden, das heisst für einzelne Balken, Platten oder Schalenelemente und schlussendlich die Effizienz der zur Zeit verwendeten FE-Methoden verbessern. Dies soll durch eine interpretierbare Mechanik-gestützte Methode, die in die FEA eingegliedert wird erreicht werden, idealerweise mit einer praxistauglichen Implementierung in einer kommerziellen FE-Software.
Zur Veranschaulichung der Idee wurde eine Vorstudie durchgeführt, die eine vereinfachte NLFEA eines Balkenelements untersucht. Abbildung 3 zeigt den Ablauf dieser vereinfachten NLFEA, bei der zuerst der einfach gelagerte Balken in finite Elemente unterteilt wird, welche auf der Querschnittsebene analysiert werden, die dann zu den Werten für die lokalen und globalen Steifigkeitsmatrizen führen, um schlussendlich das globale Gleichgewicht zu lösen. Das Ziel war nun, die iterative und zeitaufwändige Berechnung auf Querschnittsebene durch ein normales NN zu ersetzen (siehe Abbildung 3). Das NN wird auf Daten von parametrisierten Simulationen trainiert. Die Parametrisierung enthält Variationen von Materialsteifigkeiten und -stärken wie auch von Breite und Höhe des finiten Elements, etc. Zum Schluss werden dem NN als Input das Moment am finiten Element gegeben und es kann dann Krümmungen und zugehörige Tangentensteifigkeiten (EI) des Querschnitts vorhersagen. Durch den Ersatz dieses Berechnungsschrittes wird ein stellvertretendes finites Element erstellt, welches für alle mit Balkenelementen modellierbare Strukturen eingesetzt werden kann und dadurch zu grösserer Generalisierbarkeit führt. Als nächste Schritte sollen diese Resultate nun für Schalenelemente adaptiert werden und physikalische Zusammenhänge im NN eingebracht werden gemäss den Erläuterungen oben. Zuletzt wird die entwickelte ML-FEA Methode mit dem aktuellsten Stand der Technik von NLFEA Methoden verglichen.
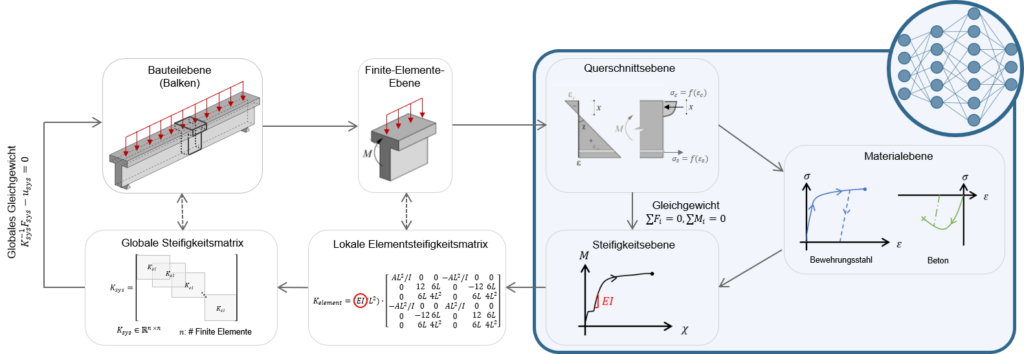
Zusammenfassend hoffen wir mit dieser Kombination von ML und FEA Methoden ein neues Werkzeug zu entwickeln, mit dessen Hilfe Entwurf und Überprüfung von bestehenden Bauten detaillierter durchgeführt werden können und somit Stahlbeton effizienter eingesetzt werden kann. Falls Sie Interesse an diesem Thema haben, bleiben Sie dran, wir werden Sie gerne über die aktuellsten Entwicklungen dieses Projekts auf dem Laufenden halten.
Vera Balmer
Link to the English version: A first step towards AI-assisted strut-and-tie model generation.
Fachwerkmodelle sind ein weit verbreiteter Ansatz zur Bemessung von in der Ebene belasteten Stahlbetontragwerken wie Balken oder Wände auf der Näherungsstufe 1. Sie sind insbesondere für geometrische oder Lastdiskontinuitäten geeignet. Mit der Fachwerkanalogie wird der Kraftfluss dargestellt, in welchem Druckstreben den Beton unter Druck und Zugstreben die Bewehrung unter Zug repräsentieren. Klassische Spannungsfelder bieten einen detaillierteren Bemessungsansatz auf der Näherungsstufe 2 an, der den Kraftfluss kontinuierlicher betrachtet. Geeignete Spannungsfelder kann man durch Berücksichtigung der Knotenbereiche aus einem Fachwerkmodell ableiten1Weitere Erweiterungen der klassischen Spannungsfelder können elastisch-plastische oder nichtlineare Materialgesetze beinhalten und werden häufig in Finite-Elemente-Modellen implementiert, wie z. B. die «Compatible Stress Field Method», die sich besonders für bestehende Tragwerke eignet.. Fachwerkmodelle und Spannungsfelder sind Lösungen nach dem unteren Grenzwertsatz der Plastizitätstheorie. Demnach lohnt es sich während der Entwurfsphase verschiedene Lösungen zu untersuchen, um diejenige zu finden, die der vollständigen Lösung am nächsten kommt, und um die zulässige Last zu maximieren. Ausserdem können sie als Plausibilitätsüberprüfung der Ergebnisse aus Finite-Element-Analysen dienen, um Modellierungsfehler zu vermeiden. Die Auswahl oder der Vorschlag geeigneter Fachwerkmodelle ist einerseits stark von der Expertise und der Erfahrung des:der Bauingenieur:in abhängig und andererseits ein zeitintensives und iteratives Verfahren2Für den historischen Hintergrund der Entwicklung von Fachwerken, lesen Sie bitte diesen Blogartikel.. Diese Punkte erschweren den breiten Einsatz von Fachwerkmodellen, welche eine interpretierbare und sichere Bemessung ermöglichen. Digitale Hilfsmittel, wie maschinelles Lernen, könnten diese Lücke schliessen. Sie könnten dazu beitragen, dass unterschiedliche Ingenineur:innen einheitlichere Entwürfe für Stahlbetonkonstruktionen erstellen, und könnten letztlich zur Qualitätskontrolle und Materialreduktion eingesetzt werden. Als erster Schritt in diese Richtung stellt dieser Artikel verschiedene Ansätze von Fachwerkmodellgenerierungsmethoden und ihre Grenzen vor, gefolgt von unserer Forschungsfrage und wie ein Hilfsmittel zur Validierung von Fachwerkmodellen uns beim Erreichen unserers Forschungsziels hilft.
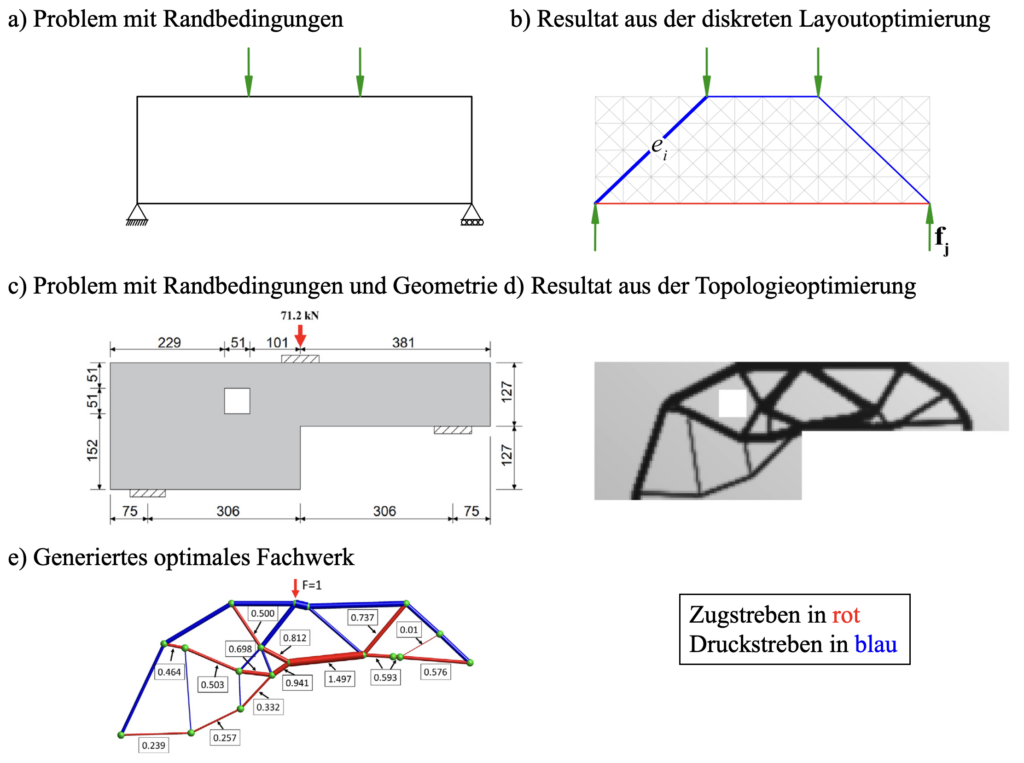
Verschiedene Ansätze wurden zur automatisierten Generierung von Fachwerkmodellen entwickelt, welche grösstenteils auf Optimierungsalgorithmen basieren. Die Mehrheit dieser Ansätze können in die folgende zwei Kategorien unterteilt werden: diskrete (Layout-) oder kontinuierliche Optimierung. Diskrete (Layout-)Optimierungsverfahren basieren auf einem vordefinierten Gitter oder Layout, das alle möglichen Knoten und Kanten des resultierenden Fachwerks darstellt (siehe Abbildung 1a-b). Mathematische Optimierungsalgorithmen werden verwendet, um eine Zielfunktion, wie z.B. das Gesamtstahlvolumen, unter vordefinierten Bedingungen zu minimieren. Aus der diskreten Optimierung erhält man ein regelmässiges Muster, wo man auch schiefe Bewehrungen pönalisieren kann, damit man ein Fachwerk mit nur orthogonaler Bewehrung erhält, aber dennoch schräge Druckstreben erlaubt.
Im Gegensatz dazu basieren kontinuierliche Optimierungsverfahren oft auf der Topologieoptimierung. Die Topologieoptimierung zielt in der Regel auf die Minimierung des Gesamtgewichts oder Volumens einer Struktur unter bestimmten strukturellen Bedingungen, wie z.B. Spannungsgrenzen oder Verformungen, indem Material entfernt wird (siehe Abbildungen 1c-d). Sie erfordert grosse geometrische Freiheiten und liefert meistens Ergebnisse basierend auf einem linear elastischen, isotropen Materialverhalten, was die Berechnungen erheblich beschleunigt. Im Falle von Stahlbeton, entspricht diese vereinfachende Annahme aber nicht dem wahren Materialverhalten, da sie den Einfluss der Bewehrungsrichtung, der Rissbildung, das unterschiedliche Materialverhalten unter Zug und Druck und andere materielle Nichtlinearitäten vernachlässigt. Die Topologieoptimierung liefert nur ein Zwischenresultat und noch nicht das finale Fachwerk (Abbildung 1d) mit spezifischen Knotenpunkten und Streben. Es ist schwierig, ein geeignetes Fachwerk zu finden, da man die Aspekte der Bauausführung (z.B. Vermeidung von schiefer Bewehrung oder die Berücksichtigung der Bewehrungsverankerung) gegenüber der strukturellen und materiellen Ausnutzung abwägen muss (Abbildung 1e).
Zusammenfassend lässt sich sagen, dass der diskrete Optimierungsansatz oft zu rigide ist, um komplexe Geometrien zu erfassen, und wenig Flexibilität für Anpassungen durch den:die Benutzer:in anbietet, während der kontinuierliche Ansatz Schwierigkeiten hat, Aspekte der Bauausführung, wie schiefe Bewehrungen oder kurze Zugstreben, zu berücksichtigen. Ausserdem wurde das Problem von mehreren verschiedenen Lastfällen, wo man für jeden einzelnen Lastfall wieder ein neues Fachwerkmodell definieren müsste, wenig erforscht. Diese Herausforderungen haben zu einer Lücke in den derzeitigen Fachwerkmodellgenerierungsmethoden geführt. Wenige kommerzielle Programme beinhalten diese optimierungsbasierten Ansätze und sie haben sich in der Praxis noch nicht durchgesetzt. Des Weiteren führen Optimierungen nur zu einem einzelnen Fachwerkmodell. Jedoch benötigt der:die Ingenieur:in Freiheiten, um andere problemspezifische und erfahrungsbasierte Aspekte zu berücksichtigen, und auch die Möglichkeit das resultierende Fachwerk zu beeinflussen, da er:sie am Ende des Tages der:die Entscheidungsträger:in bleibt. Wir möchten diese Forschungsfrage auf eine datenbasierte und domänenspezifische Weise mit Hilfe von maschinellem Lernen angehen, indem wir ein KI-gestütztes automatisiertes Fachwerkmodellgenerierungstool entwickeln. Dieses Tool konzentriert sich nicht nur auf die Generierung eines optimalen Fachwerks, sondern schlägt eine Auswahl von Fachwerkmodellen vor und erlaubt ein Zusammenspiel zwischen Benutzer:in und Maschine, um den:die Ingenieur:in im Entscheidungsprozess zu unterstützen.
Als ersten Schritt in Richtung dieses Ziels und für eine zuverlässige Datengenerierungspipeline, benötigen wir ein Validierungstool zur Überprüfung der vorgeschlagenen Fachwerke. Eine solche Pipeline wird für das Training und Testen des maschinellen Lernmodells benötigt, und um die endgültigen Vorschläge zu validieren. Dieses Tool, das derzeit nur die Traglast berücksichtigt, überprüft nicht nur das Kräftegleichgewicht, sondern auch die Spannungsfelder und Knotenbereiche, um eine verfeinerte Bemessung auf Näherungsstufe 2 zu erreichen.
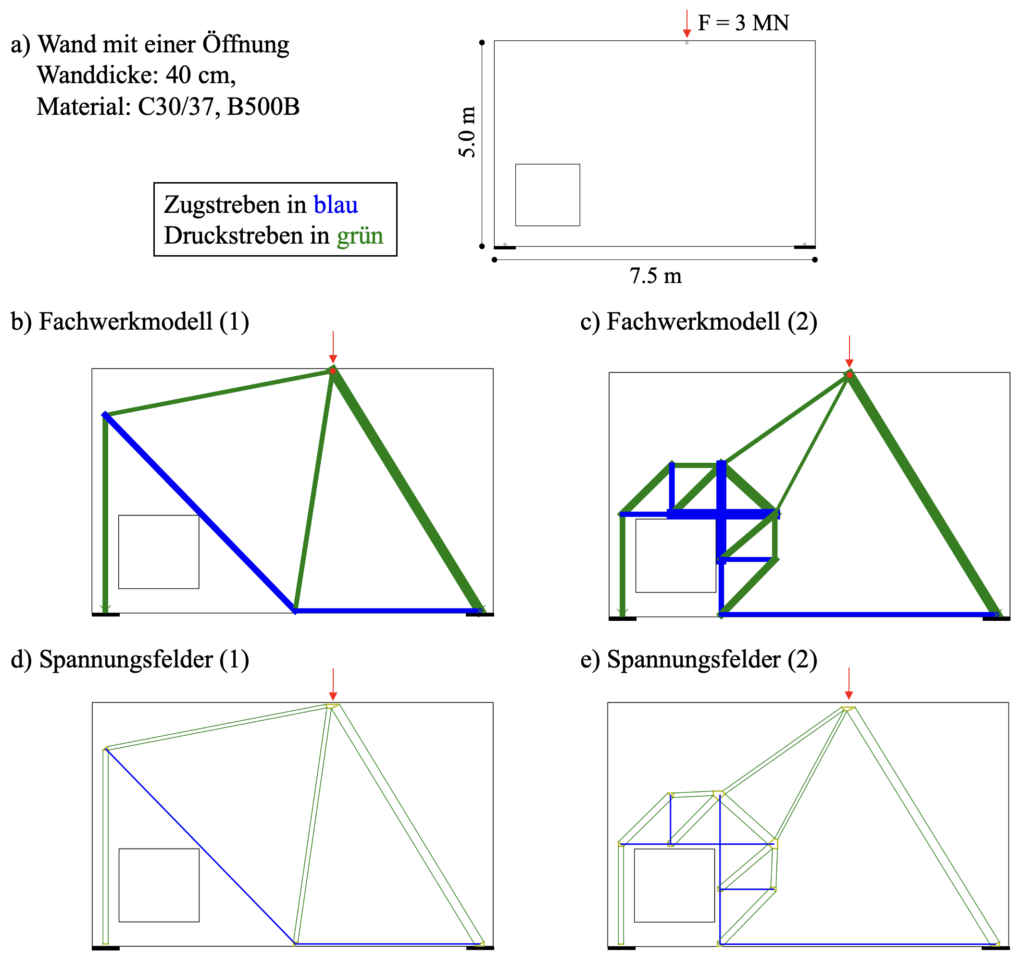
Anhand des Beispiels einer Wand mit einer Öffnung (siehe Abbildung 2a, Beispiel aus Schlaich et al. 1987) und zwei verschiedenen entsprechenden Fachwerken3Die rechte konzentrierte Druckstrebe ist eine Vereinfachung, und man sollte Querbewehrung einlegen, um die Kräfte zu verteilen., möchten wir die Notwendigkeit für die Generierung mehrerer Fachwerke aufzeigen. Das erste Modell (Abbildung 2b) veranschaulicht ein einfaches aber effizientes Fachwerk, das schiefe Bewehrung verwendet und einen geringen Gesamtstahlverbrauch aufweist. Ohne die Mindestbewehrung, die Verankerung der Bewehrung und andere konstruktive Details zu berücksichtigen, beträgt das Gesamtstahlvolumen 0.021 m3. Das zweite Modell (Abbildung 2c) zeigt ein regelmässigeres Fachwerk mit nur orthogonaler Bewehrung. Allerdings benötigt dieses Modell 70% mehr Stahl und zwar 0.036 m3. Dennoch sollte man keine voreiligen Schlüsse ziehen.
Die sichere Anwendung von Fachwerken setzt die Erfüllung der zugrunde liegenden Annahmen der Plastizitätstheorie, einschliesslich der Duktilität, voraus. Eine ausreichende Mindestbewehrung, z.B. hier 12@150 ist unumgänglich. Da die Fachwerkmodelle auf linear elastischem Materialverhalten basieren, können diese superponiert werden. Durch die Verwendung der Mindestbewehrung, kann die Traglast des zweiten Fachwerkmodells um 9% ausgenutzt werden. Dies verringert in Kombination die Last des ersten Modells, sodass dies zu einer Reduktion des Stahlvolumens um 10% führt. Es gibt selbstverständlich andere mögliche Aufteilungen. Schlaich et al. schlagen z.B. vor, dass jedes Modell die Hälfte der Last trägt. Dieses Beispiel zeigt, dass es optional ist, nur ein Fachwerk zu betrachten; stattdessen können mehrere kombiniert werden, um die Vorteile jedes Modells auszunutzen.
Das Validierungstool liefert uns die äquivalenten Spannungsfelder in den Abbildungen 2d und e, unter der Annahme einer Verankerung der Bewehrung ausserhalb der Knotenbereiche und hydrostatische Knoten. Es zeigt, ob genug Beton aktiviert werden kann und macht somit kritische Bereiche für den:die Benutzer:in ersichtlicher.
Dieses Beispiel veranschaulicht die Abwägung zwischen einem simplerem Fachwerk (1), das den Stahlverbrauch optimiert, aber die Bauausführung beeinträchtigen kann, und einem regelmässigeren Fachwerk (2) mit einem höheren Stahlverbrauch aber dafür einer einfacheren Bauweise.
Als nächsten Schritt untersuchen wir verschiedene Algorithmen und Methoden des maschinellen Lernens, um unser Problem der KI-gestützten automatischen Generierung von Fachwerkmodellen anzugehen. Dies wird jedoch ein Thema für einen zukünftigen Blogbeitrag sein. In der Zwischenzeit können Sie sich gerne an Karin Yu wenden, wenn Sie Vorschläge oder Bemerkungen haben.
Karin Yu
Link to the English version: Establishment of an inter-university research and teaching group in the field of structural masonry.
Lehre und Forschung im Bereich des konstruktiven Mauerwerkbaus haben am Institut für Baustatik und Konstruktion der ETHZ eine langjährige Tradition. Diverse Pionierarbeiten zur Beschreibung des Tragverhaltens von Mauerwerk und wegweisende experimentelle Untersuchungen an Mauerwerksbauteilen wurden ab den 70er Jahren unter der Leitung von Prof. Dr. Bruno Thürlimann und seinem Nachfolger Prof. Dr. Peter Marti durchgeführt. Diese bahnbrechenden Arbeiten fanden in der Wissenschaft einen breiten Anklang und liefern die Grundlagen für die heutige Bemessungsnorm SIA 266 und wurden an der ETHZ durch Dr. Nebojsa Mojsilovic und Prof. Dr. Joseph Schwartz fortgeführt . Die Emeritierung von Prof. Schwartz Anfang 2023 und die anstehende Pensionierung von Dr. Mojsilovic im Jahre 2025 veranlassten die Ziegelindustrie Schweiz (Weblink), eine Anschlusslösung zur Weiterführung von Lehre und Forschung im Bereich des konstruktiven Mauerwerkbaus zu finden.
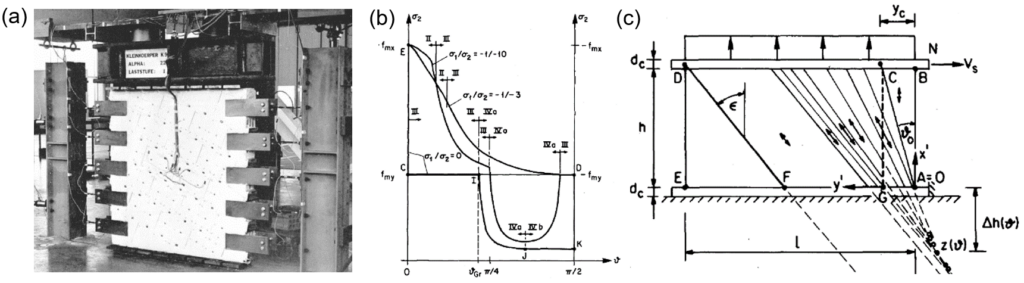
Etablierung einer hochschulübergreifenden Mauerwerksgruppe
Über Prof. Dr. Walter Kaufmann (Leiter der Professur für Massiv- und Brückenbau) bekam ich die Anfrage, ob ich künftig die Lehr- und Forschungstätigkeiten im Bereich des konstruktiven Mauerwerkbaus übernehmen möchte. In einigen Gesprächen mit der Ziegelindustrie Schweiz entwickelte sich schliesslich die Idee einer hochschulübergreifenden Mauerwerksgruppe, die ich ab diesem Sommer an der Professur für Massiv- und Brückenbau (Weblink) der ETHZ und am Institut für Bauingenieurwesen (IBI) der Hochschule Luzern Technik und Architektur (HSLU T&A) leiten darf. Die Mauerwerksgruppe wird durch eine grosszügige Donation der Ziegelindustrie Schweiz unterstützt, wobei die Vereinbarung – gemäss unseren akademischen Prinzipien – festhält, dass die Freiheit von Forschung und Lehre jederzeit gewährleistet ist. Bis zu seiner Pensionierung wird Dr. Mojsilovic die Mauerwerksgruppe mit seiner Expertise unterstützen, was sehr wertvoll ist und die Kontinuität gewährleistet.
Faszination Mauerwerk – eine uralte Bauweise in der modernen Welt
Seit meiner Studienzeit begleitet mich der Werkstoff Mauerwerk in verschiedenen Lehr- und Forschungstätigkeiten, die ich insbesondere während meines Doktorates am Institut für Werkstoffe im Bauwesen (IWB) der Universität Stuttgart bearbeitete (Publikationsliste siehe hier). Neben zahlreichen analytischen und experimentellen Untersuchungen galt meine Faszination der Beschreibung und Analyse des Tragverhaltens von Mauerwerk und Mischtragwerken (Mauerwerk/Stahlbeton) mit modernen Simulationstools – oder etwas fachtechnischer ausgedrückt, der Entwicklung von mechanisch konsistenten Modellvorstellungen und deren Implementierung in numerische Verfahren (z.B. lineare/nichtlineare Finite Elemente → siehe Blogbeitrag vom Jahre 2022). Zudem kam ich immer wieder in den Genuss, innerhalb von Lehrveranstaltungen und der Betreuung von Studierendenarbeiten das Wissen weiterzugeben.
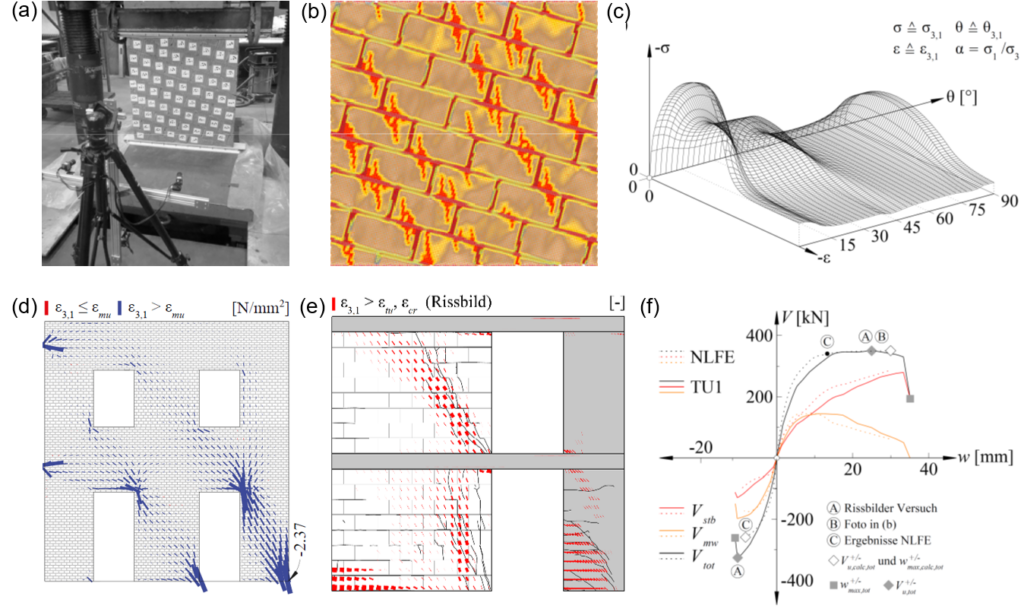
Obwohl sich die Mauerwerksbauweise1Heutzutage steht allerdings eine breite Palette von Hochleistungssteinen zur Verfügung, die je nach statischen, bauphysikalischen und ästhetischen Anforderungen verwendet werden. über Jahrtausende entwickelte, hat sich das Grundprinzip (das Aufeinanderschichten von Steinen2Heutzutage steht allerdings eine breite Palette von Hochleistungssteinen zur Verfügung, die je nach statischen, bauphysikalischen und ästhetischen Anforderungen verwendet werden.) über die kulturhistorischen Zivilisationen kaum verändert – die Art und Weise zur Analyse, Untersuchung und Berechnung jedoch radikal. Während bereits in der Antike die Römer und Griechen die selbsttragende Form von Mauerwerksgewölben erkannt hatten, beschäftigten sich in der Renaissance erste Gelehrte systematisch mit der Frage nach einer dem Kräfteverlauf angepassten Bogenform, woraus sich später die Stützlinie entwickelte – d.h. die mathematische Beschreibung der Linie in einem Bogen, entlang welcher die aus der Belastung entstehenden, zusammengefassten Druckkräfte verlaufen (vgl. Abbildung 3 (a)). Diese physikalischen Grundprinzip des Kräfteabtrages über Druckstreben macht man sich für die rechnerische Beurteilung von Mauerwerksbauten noch heute zunutze, beispielsweise bei der Überprüfung von Bogenbrücken aus Mauerwerk mittels graphischer Statik oder bei der Bemessung von herkömmlichen Mauerwerkswänden auf Basis von ideal plastischen Druckspannungsfeldern gemäss der SIA Norm 266 (vgl. Abbildung 3 (b)). Die Methodik zur Berechnung des Kräfteverlaufes und der Traglasten hat sich jedoch durch die digitale Revolution in den letzten Jahren elementar verändert. Aufwendige Rechen- und Routineaufgaben werden effizient vom Computern übernommen – die Kunst und das Wissen der baustatischen und physikalischen Grundlagen sind jedoch nicht überflüssig, sondern im Gegenteil für die Resultatinterpretation unabdingbar (und anspruchsvoller denn je!). Bereits herkömmliche Computer verfügen über genügend Rechenpower für die Verwendung von verfeinerten (z.B. nichtlinearen) Materialmodellen, womit “automatisert”3“automatisiert” bezieht sich auf den eigentlichen Berechnungs- und Optimierungsprozess des Computers. Die Anwendung, Interpretation und Verifizierung solcher verfeinerten Modellvorstellung (allen voran die nichtlineare Finite Elemente Methode) ist jedoch äusserst zeitaufwendig und verlangt ein hohes Mass an Fachkompetenz. der Kräfteverlauf berechnet werden kann (vgl. Abbildung 3 (c)) und Aussagen zum Last-Verformungsverhalten, der Rissbildung und der damit einhergehenden Schnittkraftumlagerung möglich sind (z.B. mit dem während meiner Dissertation entwickelten URM-Usermat für die nichtlineare Finite Element Analyse von allgemein beanspruchten4Unter einer allgemeinen Beanspruchung wird die Kombination aus Scheiben- und Plattentragwirkung verstanden. Mauerwerksbauteilen). Vor dieser Entwicklung darf auch die Ausbildung und Forschung im Bereich des konstruktiven Mauerwerkbaus nicht halt machen – die konsequente Anwendung des Gleichgewichts und mechanischer Grundprinzipien ist jedoch entscheidend (oder besser gesagt zwingend) für deren Erfolg.
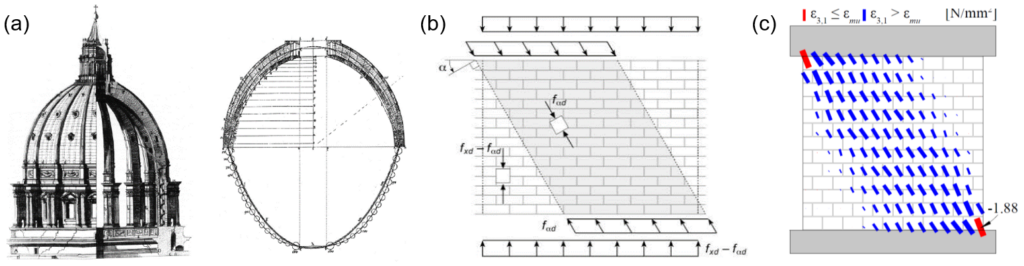
Forschung, Lehre und Praxis verbinden
Eine zentrale Aufgabe der Mauerwerksgruppe sind die Lehr- und Forschungstätigkeiten im Bereich des konstruktiven Mauerwerkbaus, die gleichzeitig an der Professur für Massiv- und Brückenbau der ETHZ und dem IBI der HSLU T&A etabliert werden. Im Fokus steht dabei insbesondere die Förderung und Entwicklung von numerischen Simulationstools für die Lösung von Problemstellungen aus der Praxis.
Forschungsschwerpunkt ist dabei die Entwicklung von mechanisch konsistenten Materialmodellen und deren Implementierung in die an der Professur für Massiv- und Brückenbau entwickelten Software- und Analysetools – wie z.B. der aktuell in Entwicklung stehenden Open-Source-Toolbox StrucEng Library (mehr dazu im Blogbeitrag aus dem Jahr 2022). Die Tools zielen drauf ab, neue Tragwerke effizienter zu entwerfen sowie Traglastreserven bestehender Tragwerke zur Minimierung von Verstärkungsmassnahmen zu identifizieren, ohne dabei die Tragsicherheit und Robustheit zu gefährden. Als Grundlage für die Entwicklung und Validierung der Materialmodelle führen wir experimentelle Untersuchungen zum Tragverhalten von Mauerwerk durch. Dazu steht unter anderem der weltweit einzigartige Large Universal Shell Element Tester (LUSET) an der Professur für Massiv- und Brückenbau der ETHZ zur Verfügung, mit dem wir das Tragverhalten von allgemein beanspruchten Schalenelementen aus Mauerwerk erstmalig experimentell untersuchen können (vgl. Abbildung 4 (b)).
Des Weiteren widmen wir uns offenen Fragestellungen zum mechanischen Tragverhalten im Bereich des konstruktiven Mauerwerkbaus, die noch nicht vollständig geklärt sind. Dazu gehören z.B. die Frage nach den Anwendungsgrenzen ideal plastischer Berechnungsmethoden (ein “ausreichendes” Verformungsmögen wird dabei vorausgesetzt) auf den Werkstoff Mauerwerk mit seinem bekanntlich stark eingeschränkten Verformungsvermögen oder dem Tragverhalten von Mischsystemen aus Mauerwerk und Stahlbeton (z.B. Lastverteilung durch die Stahlbetonplatten, Mitwirkung von Stahlbetonscheiben, Einfluss von Sturz- und Brüstungselementen). Zur Beantwortung solcher Fragestellungen kombinieren wir die numerischen Tools und mechanischen Modellvorstellungen mit grossmassstäblichen Versuchen, mit dem Ziel, entsprechende Bemessungsmodelle oder Entwurfskriterien mit direktem Nutzen für die Baupraxis abzuleiten. Im Zentrum steht dabei immer die konsequente Anwendung mechanisch konsistenter Modelle.
In Zukunft werden wir uns zudem vermehrt mit der Anwendung und Eingliederung der Softwaretools in den digitalen Planungs-, Fertigungs-, und Erhaltungsprozess von Tragwerken beschäftigen und an neuen innovativen Lösungen für digital (vor)fabrizierte Mauerwerksbauteilen forschen.

Ein zentrales Anliegen der Mauerwerksgruppe ist zudem die Sicherstellung des Transfers der Forschungsergebnisse und die Vermittlung des Fachwissens im Bereich des konstruktiven Mauerwerkbaus in die Baupraxis. Dazu gehört einerseits die künftige Bereitstellung der StrucEng Library als Open-Source-Toolbox für die freie Verwendung in der Baupraxis. Anderseits führen wir Lehrveranstaltungen an der ETHZ und HSLU durch, wobei wir Bauingenieurinnen und Bauingenieure in den Bereichen Bemessung, Entwurf und Überprüfung von Mauerwerksbauten ausbilden und im Umgang mit computerunterstützten Berechnungsmethoden sensibilisieren. Des Weiteren engagieren wir uns in Berufsverbänden und Normkommissionen, wie z.B. der Fachgruppe für die Erhaltung von Bauwerken (FEB) der SIA (Weblink) und der Normkommission SIA 266 (Weblink) und arbeiten eng mit der Industrie an nachhaltigen Lösungen für die Baupraxis.
Last but not least soll die Mauerwerksgruppe eine Plattform für den Austausch und die Diskussion im Bereich des konstruktiven Mauerwerkbaus sein, und wir laden sie daher ein, gemeinsam an den Lösungen heutiger und künftiger Herausforderungen unserer Gesellschaft zu arbeiten. Wir freuen uns, die Zukunft des Werkstoffes Mauerwerk aktiv mitgestallten zu können und danken der Ziegelindustrie Schweiz für die wertvolle Unterstützung. Let’s give masonry a new shine!
Marius Weber
Link to the English version: The path to more sustainable concrete floor slabs through digital fabrication
In Anbetracht der Klimakrise müssen die Treibhausgasemissionen drastisch reduziert werden. Dabei muss auch der Gebäudesektor, welchem rund 37 Prozent der globalen betrieblichen energie- und prozessbedingten Treibhausgasemissionen zugeordnet werden, deutlich umweltfreundlicher werden, insbesondere wenn man bedenkt, dass die benötigte Fläche für Wohnen und Infrastruktur in den kommenden Jahren massiv zunehmen wird (2022 Global Status Report for Buildings and Construction). Um diese Reduktion der negativen Umweltauswirkungen zu erreichen ist ein Umdenken auf allen Ebenen nötig. Während aktuell alternative Baustoffe in der Forschung und Praxis grosse Beachtung finden, ist die Umsetzung von effizienten Tragwerken eine oft unterschätzte Massnahme, mit welcher enorme Einsparungen erreicht werden können. (The Institution of Structural Engineers, 2022)
Da in typischen Gebäuden rund die Hälfte des Materials in Decken verbaut wird (Bischof et al. 2022), liegt es nahe, Optimierungen der Materialeffizienz in diesen Bauteilen anzustreben. Tatsächlich existieren zahlreiche praxiserprobte Deckensysteme, welche im Vergleich zu den weitverbreiteten Flachdecken massiv reduzierte Treibhausgasemissionen verursachen: Durch die Wahl von statisch effizienten Systemen wie beispielsweise Rippendecken, Kassettendecken oder Hohlkörperdecken können in Abhängigkeit der Spannweite bis zu 60% der Treibhausgasemissionen im Vergleich zu Flachdecken eingespart werden (Regúlez et al., 2022). Wieso also bauen wir auch heute noch überwiegend Flachdecken?
Dies lässt sich mit einer ganzheitlichen Betrachtung des Problems erklären: Deckensysteme werden nicht oder nur bedingt aufgrund ihrer Treibhausgasemissionen gewählt. Vielmehr sind Kriterien wie Baukosten, Bauzeit, Schallschutz, Möglichkeit zur Integration von Haustechnikeinlagen und viele weitere entscheidend. Anders ausgedrückt müssen Deckensysteme sowohl ökologisch nachhaltig (u.a. Emissionen, Ressourcenverbrauch und Abfallproduktion, Dauerhaftigkeit und gegebenenfalls Zirkularität) als auch sozial nachhaltig (u.a. Sicherheit, Funktionalität und Anpassungsfähigkeit) und wirtschaftlich nachhaltig (u.a. Kosten, Baubarkeit und Flexibilität) sein, um auf dem Massenmarkt Verbreitung zu finden und so wirkungsvoll zur Steigerung der Umweltfreundlichkeit beizutragen. Die Komplexität dieser Anforderungen ist in Abbildung 1 zusammengefasst.
Bei vielen dieser Kriterien ist die Wahl einer Flachdecke, deren Produktion jahrzehntelang optimiert wurde, vorteilhaft: Nicht nur sind Flachdecken günstig in der Erstellung, sondern sie weisen auch eine niedrige Gesamthöhe und gute akustische Schalldämmeigenschaften auf und bieten die Möglichkeit, Haustechnik als Deckeneinlagen zu integrieren. Auch nicht zu unterschätzen ist die geometrische Freiheit im Grundriss, welche durch die Wahl von Flachdecken ermöglicht wird: Die statische Effizienz, welche mit Tragsystemen wie zum Beispiel Rippendecken erreicht wird, bedingt häufig eine höhere geometrische Komplexität der Querschnitte. Wegen des dafür erforderlichen höheren Schalungsaufwandes werden solche Decken im Allgemeinen nicht im Ortbetonverfahren sondern mittels Vorfabrikation hergestellt, wobei wiederverwendbare Schalungen eingesetzt werden. Dies wiederum reduziert die geometrische Freiheit der damit herstellbaren Grundrisse, da sich solch wiederverwendbare Schalungen im Allgemeinen nur für regelmässige und sich wiederholende Grundrisse eignen. Auch tragen Deckensysteme wie Rippendecken und Hohlkörperdecken primär in eine Richtung (in Gegensatz zu Flachdecken), was die geometrische Freiheit im Grundriss weiter eingrenzt.
All diese Gründe führen dazu, dass in der Praxis trotz des in den letzten Jahren gesteigerten Nachhaltigkeitsbewusstseins die Wahl häufig auf eine emissionsintensive Flachdecke fällt.
Das innovative Feld der digitalen Fertigung mit Beton (DFB) könnte dazu beitragen, dass diese Wahl in Zukunft häufiger auf ein effizienteres Tragsytem fällt: Durch eine Vielzahl von Fertigungsverfahren, das Bekannteste davon der 3D-Druck mit Beton (3DDB), soll der Bau von geometrisch komplexen, massgefertigten Bauteilen ohne oder nur mit minimaler Schalung bei reduzierten Produktionskosten und gesteigerter Arbeitssicherheit ermöglicht werden (Wangler et al., 2016). Was diese geometrische Freiheit in der Praxis bedeuten könnte, ist in Abbildung 2 ersichtlich: Für einen Grundriss wurden eine konventionelle Flachdecke, eine Rippendecke mit geraden, regelmässigen Rippen und eine Freiform-Rippendecke, wie sie potentiell mithilfe von digitalen Fertigungsmethoden produziert werden könnte, vordimensioniert. Aufgrund des direkteren Lastabtrags sind nicht nur die potentiellen Materialeinsparungen bei der Freiform-Rippendecke grösser als bei der Rippendecke mit geraden Rippen (27% – 38% anstatt 18% – 28% weniger Betonverbrauch in der Decke), sondern es resultieren weniger Anpassungen im Grundriss (wie zum Beispiel zusätzlich benötigte Stützen).
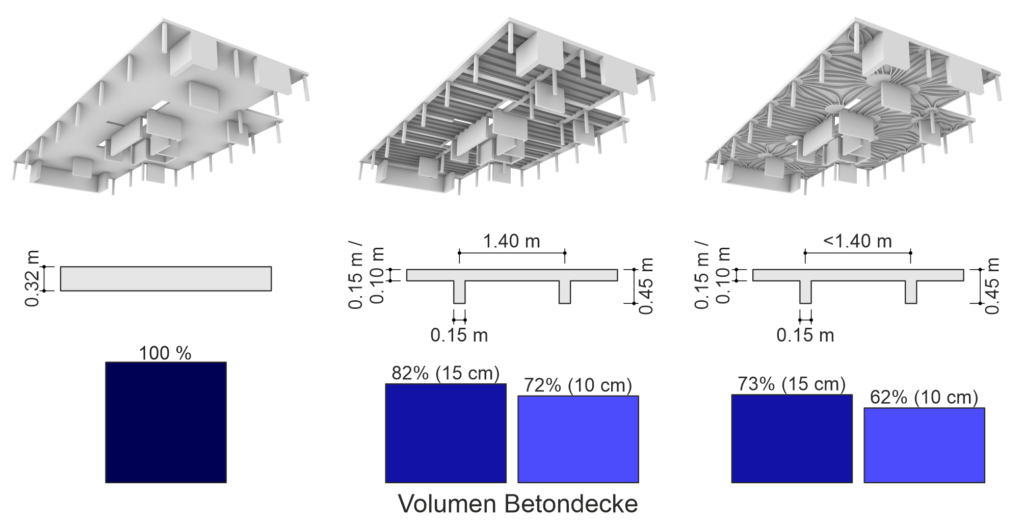
Die Herausforderung besteht nun darin, zuverlässige und effiziente Methoden zu finden, solche oder ähnliche geometrisch komplexen Tragwerke mithilfe von DFB herzustellen. Tatsächlich wurden sowohl an der ETH (im Rahmen des NFS Digitale Fabrikation) als auch weltweit bereits erste Konzepte für digital fabrizierte Betondecken entwickelt – Beispiele hierfür sind in Abbildung 3 ersichtlich. Von den meist aufwendig produzierten Prototypen zu einem massenmarkttauglichen System, welches die Möglichkeiten der digitalen Fertigung voll ausschöpft, ist es jedoch noch ein weiter Weg. Wir wollen dabei einen Beitrag leisten, indem wir Systeme entwickeln, welche DFB nur einsetzt, wo die gewonnene geometrische Freiheit vorteilhaft ist und so die Vorteile von DFB und herkömmlichen Bauverfahren vereinen.

Die Vielfältigkeit der Anforderungen, welche an Decken gestellt werden in Kombination mit den Möglichkeiten und Herausforderungen, welche DFB mit sich bringt, machen dieses Forschungsprojekt zu einer komplexen Aufgabe – es bleibt also spannend und wir freuen uns, hier zu gegebener Zeit über die Fortschritte des Projekts zu informieren.
Rebecca Ammann
Link to the English version: Production of a CFRP-Prestressed Railway Bridge Prototype.
Seit dem letzten Blogpost zum Thema ist einige Zeit vergangen, in der sich entsprechend viel getan hat. Dem Ziel, Bahnbrücken im Spannweitenbereich von 2-10 m mit karbonfaserverstärktem Kunststoff (CFK) vorzuspannen, ist das Projektteam bestehend aus SBB, alphabeton AG, HSLU, Empa und ETH einiges nähergekommen: Es ist gelungen, einen 1.7 m x 6.5 m grossen Prototypen zu bauen. Der Prototyp ist biaxial CFK-vorgespannt und repräsentiert einen Ausschnitt (bestehend aus vier anstelle von neun Längsträgern) einer Überführung mit 6 m Spannweite. Die Vorspannung ist dabei so ausgelegt, dass die Brücke unter Gebrauchslasten (LM1) ungerissen bleiben soll. Abbildung 1 zeigt die Grundidee des Brückensystems sowie den nichtrostenden Bewehrungsstahl und die sandbeschichteten CFK-Spannstäbe.

Der detaillierte Bewehrungsplan des Prototyps im Querschnitt ist in Abbildung 2 gezeigt. Er beinhaltet folgende Elemente:
- CFK-Spannstäbe (Längsvorspannung Pos. (1), Quervorspannung Pos. (2))
- Biegebewehrung der Längs- (101) und Querträger (201) aus Duplex Stahl mit Werkstoffnummer 1.4362
- Bügel und Plattenbewehrung (im Prototyp aus Kostengründen in herkömmlichem B500B Stahl)
- Aufhängebewehrung in den Kreuzungsbereichen der Längs- und Querträger (Pos. 212)
- Transportanker in den äussersten Längsträgern
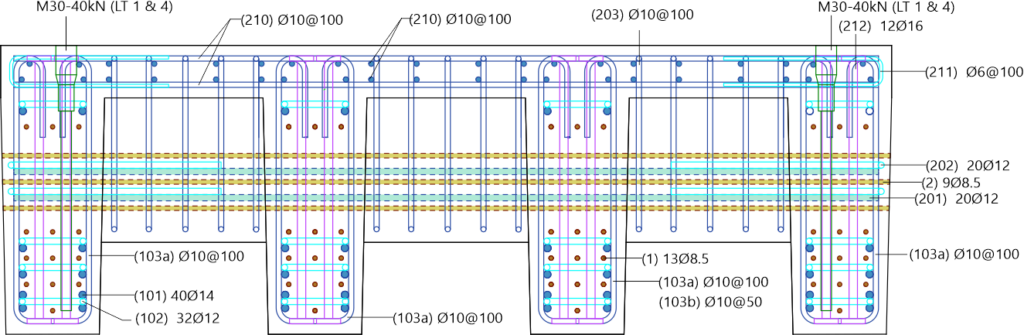
Zwei wesentliche Änderungen im Konzept und dem Herstellungsverfahren wurden seit dem letzten Blogbeitrag vorgenommen:
- Anstelle eines Ultrahochleistungsbetons (UHB) wurde ein Hochleistungsbeton C80/95 verwendet. Vorversuche haben gezeigt, dass dieser Beton ausreichend ist, um die im Spannbettverfahren vorgespannten CFK-Stäbe über Verbund zu verankern – bei wesentlich kleinerem Zementgehalt als der UHB.
- Die Herstellung erfolgte schrittweise: In einem ersten Schritt wurden die Längsträger (jeweils zwei hintereinander mit den gleichen Spannstäben vorgespannt) betoniert. Nach Fertigung der vier Längsträger wurden diese nebeneinander platziert, um die vorgespannten Querträger (Quervorspannung und -bewehrung durch Aussparungen in den Längsträgern) und die Platte zu betonieren.
Für die Herstellung (Vorspannung im Spannbettverfahren) des Prototyps waren umfangreiche Technologieentwicklung und Vorarbeiten vonnöten. Dies betrifft einerseits die Entwicklung von insgesamt vier Spannrahmen für die Vorspannung in Längs- und Querrichtung, federführend projektiert durch Prof. Dr. Albin Kenel und Martina Rohrer, HSLU. Renderings der Spannrahmen sind in Abbildung 3 zu sehen. Der Spannrahmen für die Längsträger (Abbildung 3 (a)) ist insgesamt gut 14 m lang (wobei er modular auf beliebige Längen <14 m einstellbar ist) und auf eine totale Spannkraft von 2.8 MN ausgelegt. Die drei Rahmen für die Quervorspannung (Abbildung 3(b)) müssen wesentlich weniger Last (~0.8 MN) verankern können. Das Grundsystem ist überall identisch: die CFK-Stäbe werden in Lochplatten verankert, die über hydraulische Pressen verschoben werden können, um die gewünschte Spannkraft auf die Stäbe zu bringen. Anschliessend wird um die gespannten Stäbe betoniert; die Vorspannung wird abgesenkt sobald der Beton die nötige Festigkeit aufweist.
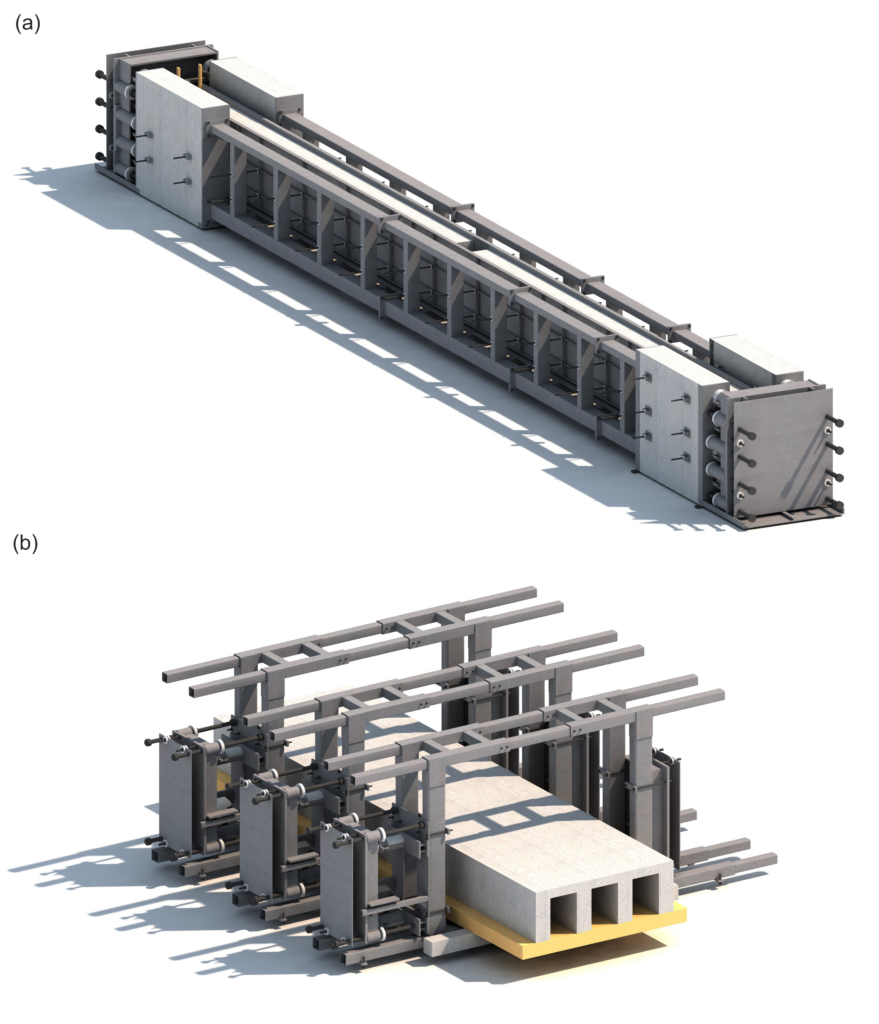
Die zweite grosse Herausforderung war die Keilverankerung der aufgrund ihrer Anisotropie äusserst anspruchsvoll zu spannenden CFK-Stäbe. Die Verankerung (entwickelt durch Prof. Dr. Giovanni Terrasi und Valentin Ott, Empa) bestehend aus einer Stahlhülse und drei Kunststoffkeilen ist auf ihrem jetzigen Entwicklungsstand in der Lage, zuverlässig eine Kraft von 55 kN pro Stab (entspricht einer Spannung von 1041 MPa bezogen auf den nominellen Durchmesser von 8.2 mm) zu verankern. Abbildung 4 zeigt (a) eine einzelne Verankerung, (b) das hydraulische Einpressen der Keile auf eine definierte Einpresskraft, sowie (c) die Anordnung der Keile in der Lochplatte für die Herstellung der Längsträger.

Abbildung 5 zeigt Bilder der Herstellung im Werk der alphabeton AG:
| (a) | Bewehrungskörbe der Längsträger im Spannrahmen. Diese mussten äusserst präzise gefertigt sein, damit die Spannglieder durchgeführt werden konnten ohne die Bewehrungseisen zu touchieren (vgl. Abbildung 2). Kontakt würde (i) zu nicht kontrollierbaren Umlenkungskräften und schlimmstenfalls Versagen der Spannstäbe führen, und (ii) das Risiko galvanischer Korrosion der Bewehrungsstäbe erhöhen. |
| (b) | Bewehrungskörbe mit den unteren Lagen der CFK-Spannstäbe inklusive der horizontal geteilten Abschalung. |
| (c) | Bewehrungskorb inklusive CFK-Spannstäbe. |
| (d) | (a) Detail der Aussparungen inklusive Aufhängebewehrung (im Kreuzungsbereich der Längs- und Querträger) und eigens für diesen Zweck an der Empa 3D-gedruckte Abstandhalter, die auf das Längseisen montiert werden konnten. So konnte die geforderte Präzision der Aussparungen für das Durchführen der Quervorspannung sichergestellt werden. |
| (e) | Längsträger in der Schalung nach dem Betonieren. |
| (f) | Platzierung der Längsträger in den Spannrahmen für die Quervorspannung. |
| (g) | Bewehrung der Endscheiben und Brückenplatte. |
| (h) | Einpressen der Keile für die Quervorspannung. Man beachte, dass während des Spannvorgangs massive Stahlplatten hinter die Verankerungen montiert wurden, um ein allfälliges unkontrolliertes Absprengen bei potentiellem Versagen der Spannstäbe zu verhindern (siehe Abbildung 3). |
| (i) | Detail der Quervorspannung in den Aussparungen der Längsträger. |
| (j) | Fertiger Prototyp: Seitenansicht. |
| (k) | Fertiger Prototyp: Ansicht von unten mit Längs- und Querträgern. |

Als Fazit lässt sich festhalten, dass die Herstellung des Prototyps wie geplant gelungen ist. Erste faseroptische Dehnungsmessungen an den CFK-Stäben zeigen, dass die Vorspannung auf einer Länge von weniger als 200 mm voll über Verbund verankert wird und die Spannbettvorspannung mit sandbeschichteten CFK-Stäben somit funktioniert. «Lessons learned» umfassen sowohl das Design als auch die Ausführung. Statische Effizienz muss sorgfältig gegen die Komplexität der Fertigung abgewogen werden; der eine oder andere Millimeter mehr zwischen CFK – und Bewehrungsstäben hätte die Herstellung des Prototyps erheblich vereinfacht. Das Vorspannen der CFK-Stäbe ist anspruchsvoll und bedarf neben massgeschneiderter Hardware wie Spannrahmen und Keilankern äusserst präziser Arbeit im Werk, insbesondere beim Binden der Bewehrungskörbe. Aus Sicht des Projektteams hat die alphabeton AG den «Proof of concept» für die Herstellung erbracht, der Weg zum Bau der ersten Bahnbrücke aus CFK-vorgespanntem Beton ist jedoch noch weit… Stay tuned!
Andreas Näsbom
Link to English version: Innovating Bridge Design: Exploring the Potential of AI-Augmented Structural Engineering
Brücken sind wichtige Infrastrukturelemente, die Gemeinden miteinander verbinden, den Verkehr begünstigen und zur wirtschaftlichen Entwicklung beitragen. Der Entwurf und Bau von Brücken erfordert eine sorgfältige Planung und technisches Fachwissen, um Sicherheit, Effizienz, Ästhetik und auch Dauerhaftigkeit zu gewährleisten. Bislang war dieser Prozess in hohem Masse von menschlichem Fachwissen und manuellen Iterationen über mehrere Teams hinweg abhängig, was zu einem langwierigen und weitestgehend starren Entwurfsprozess führte. Die jüngsten Fortschritte im Bereich der künstlichen Intelligenz (KI) haben bereits viele Forschungs- und Industriebereiche transformiert und haben zudem das Potenzial, die Art und Weise zu revolutionieren, wie Ingenieure Strukturen konzipieren, analysieren und optimieren.
An unserer Professur arbeiten wir an der Integration von modernen KI-Algorithmen in das konstruktive Ingenieurwesen. Konkret befasst sich unser laufendes Forschungsprojekt “Domain-Aware-AI Augmented Design of Bridge Structures (DAAAD_Bridges)” mit der Implementierung von generativen KI-Algorithmen für die Anwendung im Brückenbau. Zusammen mit dem Swiss Data Science Center entwickeln wir eine Deep-Learning-basierte Software-Toolbox, die als Co-Pilot in frühen Entwurfsphasen fungieren und die Stärken der KI und des Menschen kombinieren soll.
In der heutigen Praxis wird Simulationssoftware (z.B. Finite-Elemente-Software) zur Qualitätsevaluation von Entwürfen eingesetzt. Zu den wichtigen Entwurfszielen gehören Sicherheit, Gebrauchstauglichkeit, Nachhaltigkeit, Baubarkeit und Kostenminimierung. Eine detaillierte und genaue Entwurfsbewertung mit Hilfe von Simulationssoftware wird jedoch bei komplexen und hochdimensionalen Entwurfsproblemen wie Brückenbauwerken rechenintensiv. Daher ist der Einsatz moderner Simulationssoftware zeitaufwändig oder sogar unbrauchbar, wenn es darum geht, mehrere Entwurfsalternativen in einer frühen Entwurfsphase effizient zu untersuchen und zu vergleichen (siehe Abbildung 1). Die früheren Entwurfsentscheidungen sind jedoch massgeblich und erfolgsentscheid für das gesamte Bauprojekt.
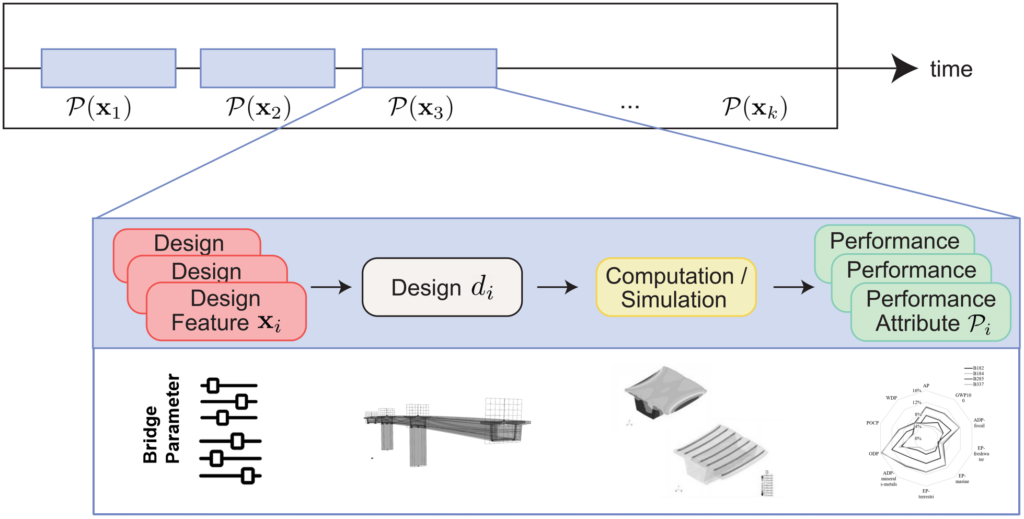
Wir stellen uns diesen Herausforderungen und formulieren den aktuellen Entwurfsprozess neu und unterstützen ihn mit datenbasierten Erkenntnissen, vgl. Abbildung 2. Wir konzentrieren uns auf Brückendesigns, die eine parametrisch Darstellung besitzen und entwickeln Deep-Learning-Modelle, die als approximative Ersatzmodelle für die Vorhersage der Qualität eines definierten Designs (“Vorwärtsdesign”) fungieren, und zusätzlich die Generierung von leistungsstarken Designalternativen ermöglichen, welche geforderte Qualitätsanforderungen erfüllen (“Inversdesign”). Das Forward-Design-Model nimmt die Entwurfsattribute (z.B. Trägerhöhe, Anzahl der Pfeiler, Materialfestigkeit, etc.) als Eingabe und approximiert die Qualität (z.B. strukturelle Ausnutzung, Treibhauspotential, Kosten, etc.) des definierten Designs. Das inverse Modell ermöglicht auf innovative Weise die Generierung einer Reihe von Entwurfsalternativen auf der Grundlage von (selbstdefinierten) Entwurfszielen und -beschränkungen (z.B. Budget, strukturelle Ausnutzungsbeschränkung, lichte Höhe, usw.).
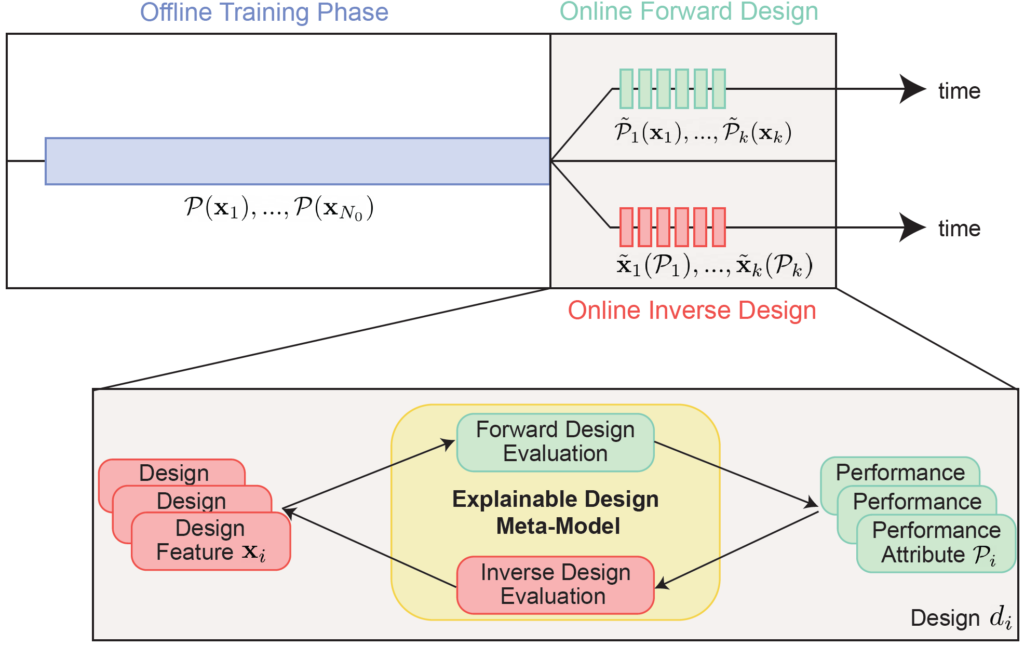
Wir haben eine Variante eines Conditional Variational Autoencoders (CVAE) abgeleitet (vgl. Abbildung 3), welche die Grundlage für die Entwurfsmetamodelle bildet. Der CVAE kann auf einem Datensatz von existierenden und/oder synthetisch erzeugten Brückenstrukturen trainiert werden. Während des Trainings werden die Modellparameter des CVAEs an die Trainingsdaten gefitted, indem die in Abbildung 3 definierte Verlustfunktion minimiert wird. Der Encoder lernt die Abbildung des euklidischen Vektors x auf den entsprechenden Leistungsvektor ŷ (Vorwärtsdesign). Zugleich lernt der Decoder, neue Deisgnattribute x̂ unter Berücksichtigung des gewählten Designzielvektors y zu erzeugen (Inversdesign). Im Anschluss an das Training wird das Modell anhand von einem Testdatenset evaluiert, welches aus Brückenstrukturen bestehen, die das Modell noch nicht zuvor gesehen hat. Da neuronale Netze vollständig differenzierbar sind, nutzt die CVAE ausserdem die automatische Differenzierung (AD) zur effizienten Berechnung der Ableitungen von den Qualitätskennwerte nach den Entwurfsvariablen (d.h. dy/dx) für eine anschliessende lokale Sensitivitäts- oder Unsicherheitsanalyse.

In einer Pilotstudie mit Basler & Hofmann wurden die entwickelten Werkzeuge auf die Projektsituation einer Fussgängerbrücke in St. Gallen angewendet [2]. Mit Hilfe von Dynamo in Revit und SOFiSTiK wurde ein Datensatz für die vorliegende reale Projektsituation generiert, auf dessen Basis der CVAE trainiert wurde. Im Projekt wurde ebenfalls eine erste Version einer grafischen Benutzeroberfläche für die Interaktion zwischen Brückeningenieur:innen und dem KI-Modell entwickelt, vgl. Abbildung 4. Es konnte gezeigt werden, dass mit dem CVAE sowohl die vorwärtsgerichteten als auch die inversen Abbildungen genau erlernt werden können und die Vorhersage der Entwurfsqualität (inkl. strukturelle Ausnutzung, Materialvolumen und Kosten) sowie die bedingte Entwurfsgeneration in Echtzeit möglich sind. Das Modell ermöglicht daher eine schnelle Untersuchung einer grossen Anzahl von Entwurfsalternativen und die Ermittlung optimaler Entwürfe, die die vorgegebenen Designziele erfüllen. Durch die Anwendung von Sensitivitätsanalysen liefern die trainierten Modelle ein Verständnis für die Abhängigkeiten der Designqualitäten von den Designattribute in den hochdimensionalen Entwurfsräumen und ermöglichen die Ableitung von Entwurfsregeln für die analysierten Strukturen. Das Tool kann daher wichtige Entscheidungen in der Konzeptionsphase eines Bauprojektes unterstützen und so Strukturen fördern, die sich durch Effizienz, Wirtschaftlichkeit und Umweltverträglichkeit auszeichnen. Die Einschränkung besteht darin, dass der Aufbau der Datengenerierungspipeline, die Datengenerierung und der Trainingsprozess selbst (d.h. die Offlinephase, vgl. Abbildung 2) einen erheblichen Zeitaufwand erfordern. Daher sollten die datengestützten Entwurfsmodelle so allgemein wie möglich anwendbar erstellt werden, was zum Beispiel durch die Erweiterung der Trainingsdatenbank um mehrere Projektsituationen und Brückenbauwerkstypen erreicht werden kann. Die Studie zeigt ausserdem die Notwendigkeit und das Potenzial systematischer und detaillierter Datenbanken, welche die geplanten und gebauten Strukturen von heute und morgen enthalten.
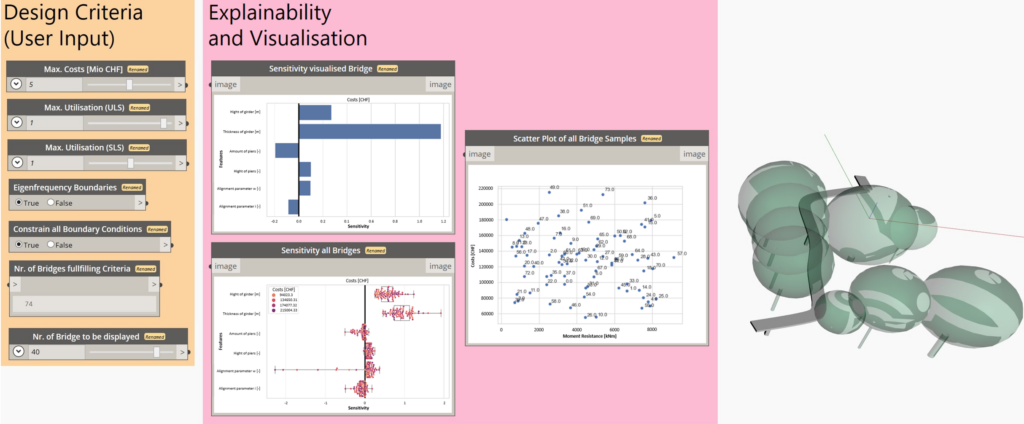
Die sich in der Entwicklung befindende Software-Toolbox ist strukturunabhängig anwendbar und kann daher ein breites Spektrum parametrischer Entwurfsprobleme unterstützen. Die breite Anwendbarkeit unseres Ansatzes demonstrieren wir mit einigen Anwendungsstudien, zum Beispiel des Entwurfes von Stahl- und Holzgitterschalentragwerken in Zusammenarbeit mit der Digital Structures Gruppe des MITs [3] und der Holzverbindungsbemessung mit der Holzbaugruppe der ETH. Klingt spannend? Fühlen Sie sich eingeladen, einen Blick auf die Projekt-Webseiten zu werfen oder uns zu kontaktieren, wenn Sie daran interessiert sind, unsere Toolbox in Ihrem Forschungsprojekt oder Ihrem laufenden Projekt in der Industrie einzusetzen.
Sophia Kuhn
Literatur
| [1] | Kuhn, S. V., Hodel, A., Bischof, R., Balmer, V. M., Perez Cruz, F., Kaufmann, W., Kraus, M. A. (2023). Assessment and Integration of Sustainability and Circularity Metrics within Generative Bridge Design. International Conference on Intelligent Computing in Engineering, London. https://doi.org/10.3929/ethz-b-000646105 |
| [2] | Balmer, V. and Kuhn, S. V., Bischof, R., A., Salamanca, L., Kaufmann, W., Perez-Cruz, F., Kraus, M. (2024). Design Space Exploration and Explanation via Conditional Variational Autoencoders in Meta-Model-Based Conceptual Design of Pedestrian Bridges. Automation in Construction, 163, 105411. https://doi.org/10.1016/j.autcon.2024.105411 |
| [3] | Fang,D., Kuhn, S. V., Kaufmann, W. , Kraus, M. A., Mueller, C. (2023). Quantifying the influence of continuous and discrete design decisions using sensitivities. Advances in architectural geometry, Stuttgart. https://doi.org/10.1515/9783111162683-031 |
Links
https://mkrausai.github.io/research/01_SciML/01_BH_PedestrianBridge_XAI/
Link to the English version: Developing a material model for reinforced concrete structures subjected to cyclic loading
An der Professur für Massiv- und Brückenbau setzen wir seit einigen Jahren ein selbst entwickeltes Materialmodell für Simulationen von Stahlbetonstrukturen ein, unter anderem für Nachrechnungen von bestehenden SBB Rahmenbrücken. Die Simulationen werden auch nicht-lineare Finite-Elemente (NLFE) Analysen genannt. Mehr über den Begriff “NLFE Analysen” können Sie im Blogbeitrag “Die Finite-Elemente-Methode im konstruktiven Ingenieurbau” lesen. Wie in diesem beschrieben wird, besteht das Grundprinzip von FE Analysen in der Tragwerksplanung darin, eine komplexe Tragstruktur in viele Elemente zu unterteilen (Diskretisierung) und die Elemente mathematisch zu einem Gesamtmodell zu verknüpfen. Für eine FE Analyse wird neben der Geometrie der Tragstruktur, der Einwirkung und den Randbedingungen/Lagerung auch ein Materialmodell benötigt, um (auf der Elementebene, präziser gesagt im Integrationspunkt) aus den Verformungen, resp. Dehnungen, die zugehörige Kraft, resp. Spannung zu berechnen. Das an unserer Professur verwendete nicht-lineare Materialmodell, genannt CMM-Usermat, simuliert die Steifigkeiten (= Kraft / Verformung resp. = Spannungen / Dehnungen) von Scheiben-, Platten und Schalenelementen akkurat, und die in Versuchen beobachteten Verformungen, Versagensarten und Maximallasten werden vom Modell im Allgemeinen gut abgebildet. Für einen vertieften Einblick in den Aufbau und Verifikation des Materialmodelles verweise ich auf folgende Literatur: [1]–[4]. Das CMM-Usermat ist zurzeit auf unidirektionale Belastungen beschränkt, d.h. es können nur monoton ansteigende Belastungen berücksichtigt werden; Ent- und Wiederbelastungen können nicht simuliert werden.
Als logischer nächster Schritt in der Entwicklung des Materialmodelles soll es verallgemeinert werden, damit Ent- und Wiederbelastungen / zyklische Belastungen aufgebracht werden können. Dies ermöglicht es uns, Simulationen der Tragstrukturen für verschiedene Zeitpunkte der zyklischen Belastung (z.B. bei einem Erdbeben) durchzuführen, auch bezeichnet als Zeitverlaufsanalyse. In meinem Doktorat befasse ich mich mit dieser Weiterentwicklung des Materialmodelles. Ziel des Forschungsprojektes ist es, mit dem zu entwickelnden zyklisches Materialmodell stabile und zuverlässige FE Analysen durchzuführen, die das Tragverhalten von zyklisch beanspruchten Stahlbetonstrukturen möglichst exakt wiedergeben. Caminada hat sich im Rahmen von seinem Masterstudium an der Hochschule Luzern (HSLU) bereits dieser Thematik angenommen und vielversprechende Resultate erzielt [5]-[7], die eine vertiefte Erforschung rechtfertigen.
Finanzierung des Forschungsprojektes:
Das in diesem Blogbeitrag beschriebene Forschungsprojekt, das auf drei Jahre ausgelegt ist und 2025 endet, wird vom Eidgenössischen Nuklearsicherheitsinspektorat (ENSI) finanziert und von seinen Fachexpert:innen begleitet. Ein Forschungsschwerpunkt des ENSIs liegt bei der Erdbebenanalyse von Stahlbetontragwerken mit dominanter Scheibentragwirkung (Schubwände). Mit den Erkenntnissen aus diesem Projekt sichert das ENSI seine Kompetenz bei der Bewertung der Tragsicherheit solcher Tragelemente. Weitere Informationen zur Forschung des ENSI findet man im jährlich erscheinenden Erfahrungs- und Forschungsbericht.
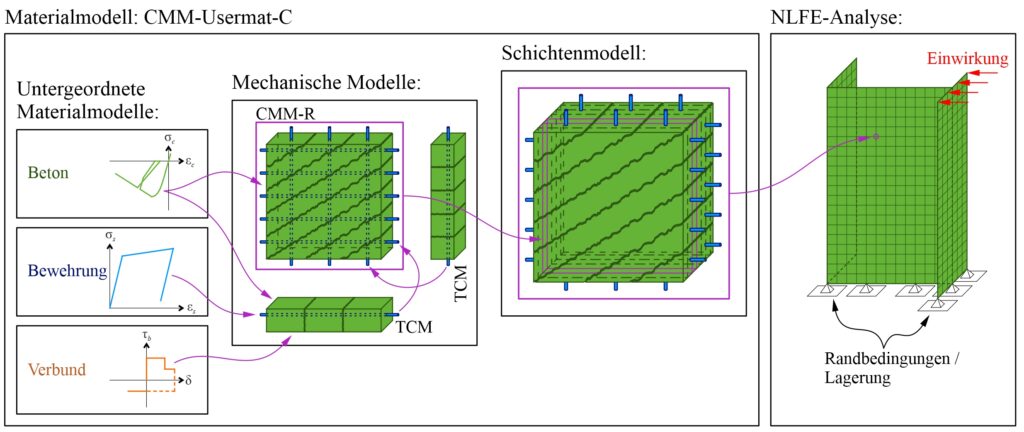
In der Folge wird der Aufbau des zyklischen Materialmodelles beschrieben, wobei CMM-Usermat-U bzw. CMM-Usermat-C das unidirektionale bzw. zyklische Materialmodell bezeichnet.
Stahlbeton in a nutshell (für Nicht-Bauingenieur:innen):
Beton hält einer relativ hohen Druckbelastung stand, aber wenn er auf Zug beansprucht wird, ist die maximal aufnehmbare Last eine Grössenordnung kleiner, wobei das Versagen auch noch spröde ist. Die tiefe und stark streuende Betonzugfestigkeit wird daher meist vernachlässigt bei der Bemessung der Tragsicherheit. Beton wird jedoch mindestens in zwei Richtungen (normalerweise senkrecht zueinander) mit duktilem Stahlstäben (Bewehrung), die im Vergleich zu Beton eine sehr hohe Zugfestigkeit aufweisen, verstärkt. Die Kombination von Beton und Bewehrung führt zum charakteristischen Tragverhalten von Stahlbeton: Zugkräfte werden von der Bewehrung übernommen (nachdem der Beton gerissen ist) und Druckkräfte werden überwiegend vom Beton abgetragen.
Wie dieser kurzen Beschreibung der Bestandteile und des Tragverhaltens zu entnehmen ist, kann Stahlbeton nicht als homogenes isotropes Material betrachtet werden. Das Zusammenwirken der Bewehrungsstäbe mit dem umhüllenden Beton ist sehr komplex und daher erfordert die Modellierung gewisse Vereinfachungen.
Um eine gute Näherungslösung für das komplexe Stahlbetontragverhalten zu erhalten, wurde beim CMM-Usermat-C ein Ansatz gewählt, der in drei Ebenen gegliedert werden kann: Untergeordnete Materialmodelle, mechanische Modelle und Schichtenmodell (siehe Abbildung 1).
Die untergeordneten Materialmodelle beschreiben die Spannungs-Dehnungsbeziehungen der Stahlbetonkomponenten (Beton und Bewehrung) sowie die Verbundspannungs-Schlupfbeziehung zwischen Beton und Bewehrung. Eine Bibliothek von verschiedenen untergeordneten Materialmodellen für Beton, Bewehrung und Verbund wird zurzeit aufgebaut.
Die mechanischen Modelle, die das Herzstück des CMM-Usermat-C darstellen, abstrahieren das Tragverhalten von Stahlbetonelementen so, dass die wesentlichen Mechanismen, unter anderem das Zusammenwirken der Stahlbetonkomponenten, abgebildet werden. Der Fokus liegt dabei auf einer mechanisch konsistenten Modellierung, bei der das Gleichgewicht der Kräfte und die Kompatibilität (Dehnungen und Spannungen stimmen in jedem Punkt mit den beschriebenen untergeordneten Materialmodellen für Bewehrung und Beton überein) erfüllt sind. Konkret basiert das CMM-Usermat-C auf dem Zuggurtmodell [8] (auf Englisch: Tension Chord Model (TCM)), welches die Mitwirkung des Betons zwischen den Rissen (Zugversteifung) mitberücksichtig und dem Gerissenen Scheibenmodell mit frei rotierenden Rissen [9] (auf Englisch: Cracked Membrane Model with rotating, stress-free cracks (CMM-R)), das den Lastabtrag von primär auf Schub belasteten Scheiben modelliert. Das TCM und das CMM-R greifen für das Materialverhalten der Komponenten auf die Bibliothek der untergeordneten Materialmodelle zurück. Nebenbemerkung: Der Name des Materialmodelles CMM-Usermat-C leitet sich vom verwendeten mechanischen Modell CMM-R ab, wobei «Usermat» für «user-defined material» steht.
Die dritte und höchste Ebene im CMM-Usermat-C bildet das Schichtenmodell [10], das für die Erweiterung von den bisher diskutierten mechanischen Modellen (1D und 2D) zu dreidimensionalen Platten- oder Schalenelementen zuständig ist. Dabei wird das Schalen- oder Plattenelement in Schichten unterteilt, wobei für jede Schicht ein ebener Spannungszustand angenommen wird. Die einzelnen Schichten können mit den oben beschriebenen mechanischen Modellen simuliert werden. Alle resultierenden Kräfte in den Schichten werden addiert/integriert und ergeben schlussendlich die allgemeine Beanspruchung (Membrankräfte, Biegung und Drillung) an einem bestimmten Punkt im FE-Netz.
Nachdem der gesamte Aufbau des CMM-Usermat-C erklärt wurde, beschreiben die beiden nächsten Abschnitten die konkrete Erweiterung des TCM auf zyklische Belastungen und die Verifikation des TCM für zyklische Belastungen anhand von Nachrechnungen eines zyklisch belasteten Zuggurtversuches.
Erweiterung des TCM auf zyklische Belastungen
Das TCM wird im CMM-Usermat-C gebraucht, um die Beziehung zwischen durchschnittlicher Längsdehnung und Stahlspannung am Riss für ein auf Zug belastetes 1D-Stahlbetonelement zu simulieren. Eine analytische Lösung für die Beziehung zwischen durchschnittlicher Längsdehnung und Stahlspannung am Riss, wie sie für unidirektionale Belastung (CMM-Usermat-U) verwendet wird, ist bei zyklischen Beanspruchungen, angesichts der unendlichen Anzahl möglicher Lastverläufe, schwierig zu erreichen. Daher wurde eine algorithmische Lösung implementiert, in der der 1D-Zuggurt in endliche Tranchen unterteilt und Spannungen, Dehnungen und Verschiebungen in der Bewehrung und im Beton Tranche für Tranche berechnet werden (siehe Abbildung 2). Es wird angenommen, dass die Verbundschubspannung über die Dicke der Tranchen konstant ist. Alle Variablen (σs, σc, εs, εc, us, uc, wr) ausser der Verbundschubspannung (τb) werden an den Gitterpunkten zwischen zwei benachbarten Tranchen ausgewertet. Anhand von Gleichgewichtsüberlegungen können die Spannungen in der Bewehrung, dem Beton und die Verbundschubspannungen bestimmt werden. Mit den untergeordneten Materialmodellen können die berechneten Spannungen in der Bewehrung (σs,i) oder im Beton (σc,i) am Gitterpunkt i mit den Dehnungen (εs,i, εc,i) oder Verbundspannungen (τb,k) in Beziehung gesetzt werden.
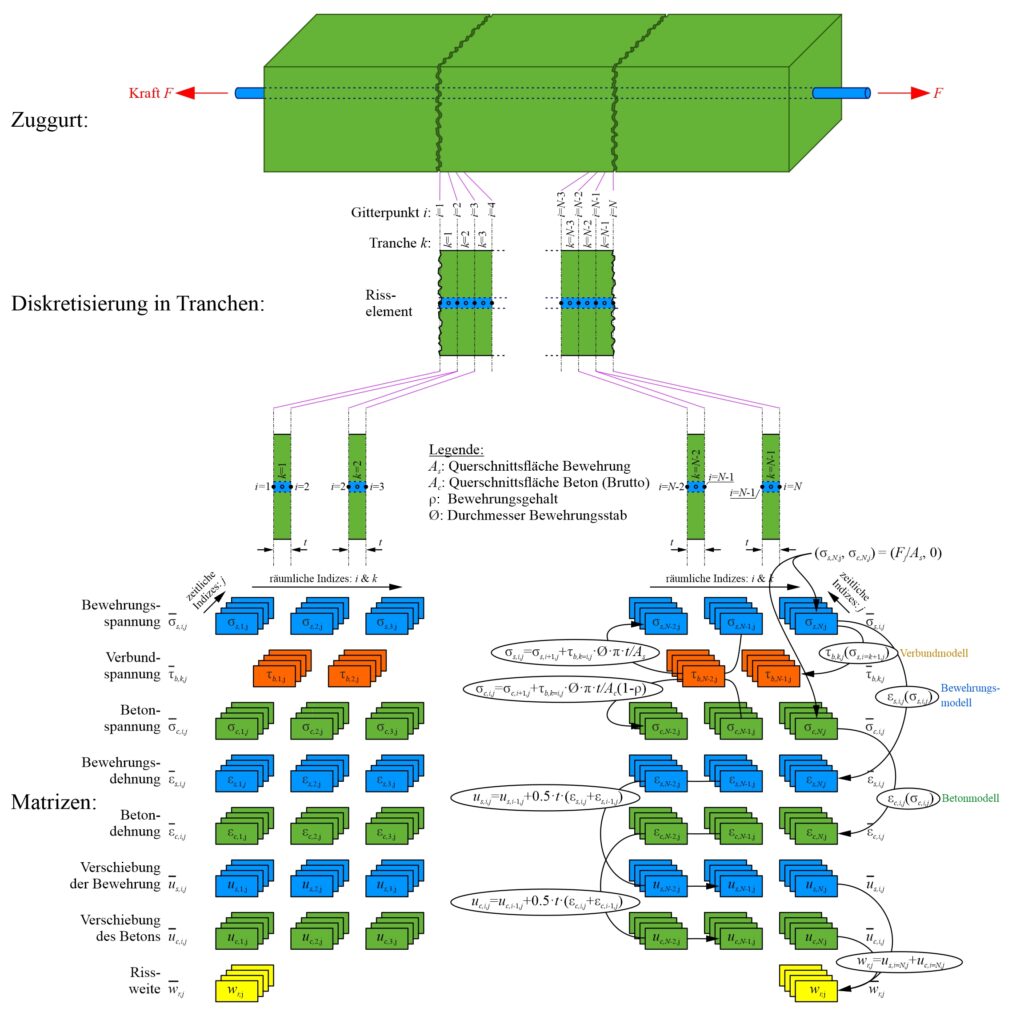
Verifikation des TCM für zyklische Belastungen
Mit dem in Python implementierten Algorithmus des zyklischen TCM können Zugversuche an Stahlbetonelementen simuliert werden. Die Ergebnisse von drei Simulationen und einem von Pfyl [11] durchgeführten Versuch sind in Abbildung 3 dargestellt. Der Stahlbeton-Zuggurt wird belastet, bis sich Risse bilden. Nach einem weiteren Lastanstieg überschreitet die Bewehrung die Fliessgrenze. Die Last wird danach auf null reduziert und wieder erhöht, bis das Versagen erreicht ist. Abbildung 3 zeigt, dass die TCM-Simulationen das Gesamtverhalten gut wiedergeben, wobei es erhebliche Unterschiede zwischen den Verbundmodellen {voller Verbund; Koppitz et al. [12]} und {kein Verbund} gibt. Letzteres berücksichtigt die Zugversteifung im gerissenen elastischen Bereich nicht und überschätzt die Verformungen im plastischen Bereich. Die TCM-Simulationen mit den Verbundmodellen {voller Verbund; Koppitz et al. [12]} überschätzen die Energiedissipation während der Ent- und Wiederbelastung (Hystereseschleife), wobei das Verbundmodell {Koppitz et al. [12]}, das eine Verbundschädigung nach dem ersten Lastwechsel berücksichtigt, weniger von der experimentellen Kurve abweicht als das Verbundmodelle {voller Verbund}. Die Ergebnisse der Simulationen sind im Allgemeinen zufriedenstellend.
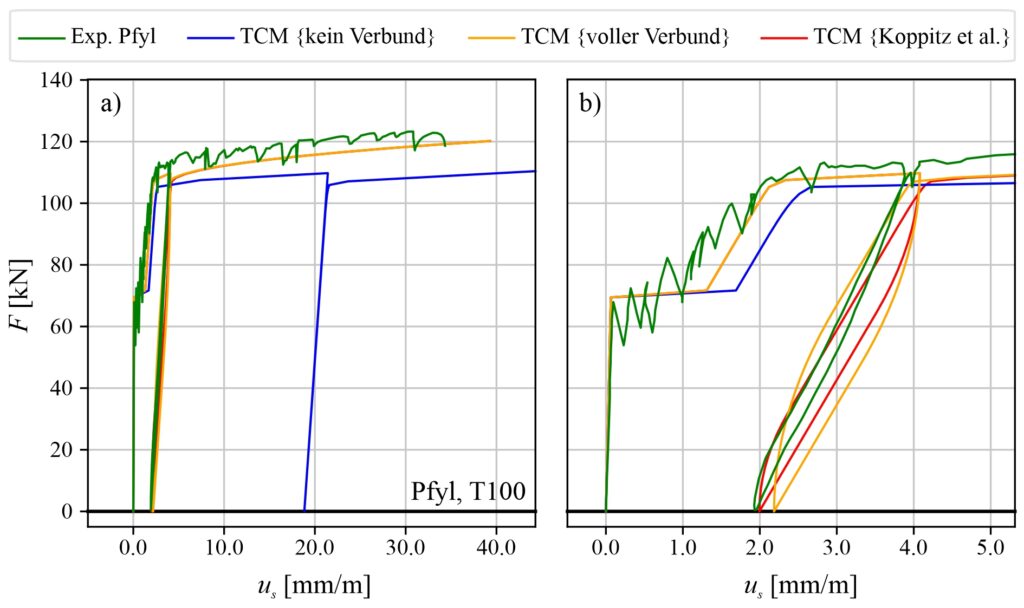
Weitere Beschreibungen und Ergebnisse werden folgen, sobald das Projekt weiter fortgeschritten ist.
Simon Karrer
Literatur
[1] P. Roos, “FEM Modelle für Stahlbetonplatten – Verifizierung des Schichtenmodells anhand von Bauteilversuchen”, Hochschule Luzern Technik & Architektur, Horw, 2014.
[2] K. Thoma, P. Roos, and M. Weber, “Finite-Elemente-Analyse von Stahlbetonbauteilen im ebenen Spannungszustand”, Beton- und Stahlbetonbau, vol. 109, no. 4, pp. 275–283, 2014, doi: 10.1002/best.201300087.
[3] K. Thoma, P. Roos, and G. Borkowski, “Finite Elemente Analyse von Stahlbetonplatten”, Beton- und Stahlbetonbau, vol. 109, no. 12, pp. 895–904, 2014, doi:10.1002/best.201400047.
[4] K. Thoma, “Finite element analysis of experimentally tested RC and PC beams using the cracked membrane model”, Engineering Structures, vol. 167, no. 15, pp. 592–607, Jul. 2018.
[5] T. Caminada, “Zuggurtmodell – zykische Beanspruchug”, Vertiefungsmodul I, Fachgruppe Massivbau HSLU, Horw, 2017
[6] T. Caminada, “Normalkraft beanspruchte Betonelemente”, Vertiefungsmodul II, Fachgruppe Massivbau HSLU, Horw, 2017
[7] T. Caminada, “Gerissenes Scheibenmodell für zyklische Beanspruchungen”, Master’s Thesis, Fachgruppe Massivbau HSLU, Horw, 2018
[8] P. Marti, M. Alvarez, W. Kaufmann and V. Sigrist, “Tension Chord Model for Structural Concrete”, Structural Engineering International, vol. 8, no. 4, pp. 287–298, Nov. 1998, doi: 10.2749/101686698780488875.
[9] W. Kaufmann, “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces”, Doctoral dissertation, Institut für Baustatik und Konstruktion, ETH Zürich, Basel, 1998. doi: 10.1007/978-3-0348-7612-4.
[10] H. Seelhofer, Ebener Spannungszustand im Betonbau: Grundlagen und Anwendungen. Zürich: vdf Hochschulverl. an d. ETH, 2010.
[11] T. Pfyl and P. Marti, Versuche an stahlfaserverstärkten Stahlbetonelementen, vol. 268. 2001. [Online]. Available: https://doi.org/10.3929/ethz-a-004273447
[12] R. Koppitz, A. Kenel, and T. Keller, “Tension Chord Model Modification for Uniaxial Unloading and Reloading in Elastic and Plastic States”, Journal of Structural Engineering, vol. 140, no. 10, p. 04014077, Oct. 2014, doi: 10.1061/(ASCE)ST.1943-541X.0000999.
Link to the English version: Load-bearing behaviour of reinforced concrete tunnel lining joints
Es mag überraschen, dass sich der Lehrstuhl für Massiv- und Brückenbau auch mit Tunnelbau befasst. Allerdings werden beim Vortrieb von Tunnel mittels Tunnelbohrmaschine (TBM) häufig Tunnelauskleidungssegmente, die sogenannten Tübbinge, aus Betonfertigteilen verwendet. Aufgrund der grossen Anzahl der benötigten Segmente kann dessen Optimierung einen grossen Einfluss auf das Tunnelbauprojekt haben. Schlankere Tübbinge können die Kosten und die Umweltauswirkungen erheblich reduzieren, da eine dünnere Auskleidung nicht nur weniger Baumaterial verbraucht, sondern vor allem auch den erforderlichen Aushub verringert.
Die Tübbinge übernehmen eine Vielzahl von Aufgaben: Sie nehmen den Gebirgsdruck auf, dichten den Tunnel ab, dienen als Befestigungselemente von Ausrüstungsteilen und übertragen die Vortriebs- und Steuerungskräfte der TBM. Die entsprechenden Kräfte müssen bei der Bemessung der Tübbinge berücksichtigt werden, wobei den Fugen eine Schlüsselrolle zukommt.
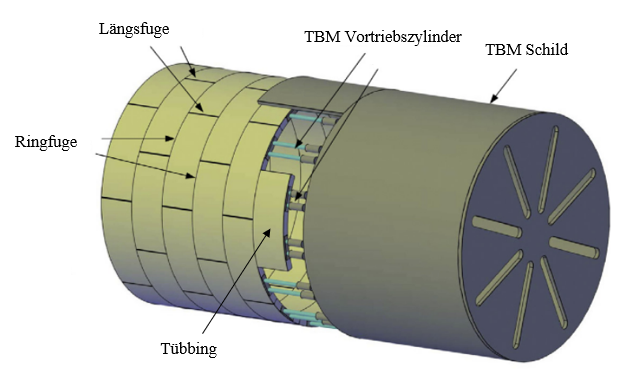
Die Längsfugen zwischen den Segmenten (siehe Abbildung 1) übertragen bei einschaligen Tunnel die Lasten während des Baus und der gesamten Lebensdauer. Im druckhaften und quellfähigen Gebirge treten typischerweise grosse Ringdruckkräfte auf. Die Kontaktfläche in der Längsfuge ist meistens im Vergleich zum Normalquerschnitt des Tübbings reduziert. Dies erleichtert den Tübbingeinbau, vermeidet Abplatzungen und ermöglicht das Anbringen von Dichtungen. Aufgrund der verringerten Kontaktfläche resultieren im Bereich der Lasteinleitung höhere Druckspannungen als im Normalquerschnitt des Tübbings und es treten Spaltzugkräfte aufgrund der Lastausbreitung auf. Die Tübbingstärke von Tunnel mit grossen Ringdruckkräften wird häufig durch die Gestaltung der Längsfugen bestimmt.
Im Schildvortrieb wirken die über den Umfang verteilten Einzellasten der TBM-Vortriebszylinder auf den zuletzt eingebauten Tübbingring und werden über die Ringfugen auf die zuvor eingebauten Tübbingringe übertragen (siehe Abbildung 1). Aus dieser Einwirkung resultieren unter anderem Zugsbeanspruchungen, aufgrund der Lastausbreitung und Einbautoleranzen, welche häufig massgebend sind für die Bemessung der Bewehrung zur Begrenzung der Rissbreiten.
Ein vom ASTRA und BAV unterstütztes Forschungsprojekt am Lehrstuhl für Massiv- und Brückenbau untersucht die Längs- und Ringfugen von Tunneltübbingen. Das Ziel des Projekts ist es, verbesserte Bemessungsansätze zur Dimensionierung der Fugen zu entwickeln. Dieser Blogbeitrag fokussiert auf die Längsfugen und präsentiert die Ergebnisse einer experimentellen Versuchskampagne.
Der Lastabtrag in den Längsfugen stellt ein Problem der Teilflächenpressung mit überwiegend unidirektionaler Lastausbreitung dar und kann als Streifenbelastung idealisiert werden. Bei der Streifenbelastung wird ein Bauteil über eine schmalere Breite als die Bauteilbreite und über eine wesentlich grössere Länge belastet. Die Last breitet sich aus, bis der gesamte Querschnitt homogen belastet wird. Aus umfangreichen Versuchsreihen ist bekannt, dass bei Teilflächenbelastung wesentlich höhere Kontaktpressungen als die einaxiale Betondruckfestigkeit auftreten können. Die meisten aktuellen Bemessungsansätze zur Teilflächenbelastung (z.B. SIA 262, Eurocode 2 oder fib Model Code 2010) basieren auf dem sogenannten Quadratwurzelansatz. Dabei wird die mittlere Tragfähigkeit der belasteten Fläche, ausgedrückt als Spannung qx,u, mit der einachsigen Druckfestigkeit fc und der Quadratwurzel aus dem Verhältnis der für den Lastabtragung zur Verfügung stehenden Fläche Ac2 und der belasteten Fläche Ac1 in Beziehung gesetzt:
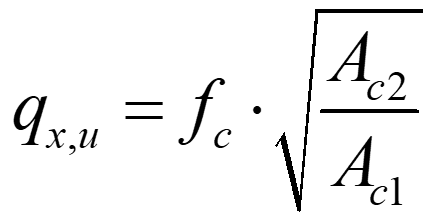
Der Quadratwurzelansatz ist rein empirischer Natur und daher ist dessen Anwendung in den Normen durch mehrere Bedingungen begrenzt: Geometrische Ähnlichkeit der Flächen Ac1 und Ac2, Begrenzung des Festigkeitszuwachses auf den Faktor drei und ausreichend Querbewehrung zur Aufnahme der Spaltzugkräfte. Dabei schränkt die erste Bedingung die Festigkeitserhöhung für Längsfugen in Tunneltübbingen stark ein. Der erforderliche Widerstand der Spaltzugbewehrung kann mit einem einfachen Fachwerkmodell zuverlässig bestimmt werden. Dabei ist es wichtig zu erwähnen, dass mit dem Quadratwurzelansatz weder die positive Wirkung der Querbewehrung, die sich in der Nähe des Lasteinleitungsbereichs befindet, noch die der Spaltzugbewehrung, die die erforderliche Mindestmenge überschreitet, berücksichtigt wird. Experimente an Tübbinglängsfugen haben gezeigt, dass wesentlich höhere Lasten aufgenommen werden können, als mit dem Quadratwurzelansatz vorhergesagt. Die Durchführung projektspezifischer Tests ist jedoch teuer und zeitaufwändig.
Als Alternative zum Quadratwurzelansatz können Längsfugen von Tunneltübbingen als Bauteile mit Umschnürungsbewehrung, z.B. nach SIA 262, Ziffer 4.2.1.8, bemessen werden. Dieser mechanisch solide Ansatz, der vor allem bei der Bemessung von Vorspannverankerungen und Druckgliedern verwendet wird, ermöglicht die Aktivierung der Querbewehrung, sowohl in der Nähe der Lasteinleitung als auch der Spaltzugbewehrung, die über das für die Lastausbreitung erforderliche Mindestmass hinausgeht. Dabei wird jedoch der günstige Einfluss der Lastausbreitung bei Teilflächenbelastung vernachlässigt. Zudem bestehen Unsicherheiten, inwieweit die Bewehrung aktiviert werden kann und ob bereits im Grenzzustand der Gebrauchstauglichkeit Abplatzungen des Überdeckungsbetons auftreten können. Nach SIA 262 ist die Kombination des Quadratwurselansatzes mit der günstigen Wirkung der Umschnürungsbewehrung nicht zulässig. Es ist jedoch bekannt, dass sich die Lastausbreitung und die Umschnürungsbewehrung positiv auf die Tragfähigkeit von teilbelasteten Flächen auswirken.
In der Vergangenheit wurden nur wenige Versuche an streifenbelasteten Stahlbetonkörpern mit ausgeprägter Umschnürungsbewehrung durchgeführt. Aus diesem Grund wurde eine Versuchskampagne mit 20 streifenbelasteten Stahlbetonblöcken (350x550x525 mm3) entworfen. Die Proben wurden mittels einer 20 MN Amsler Prüfmaschine an der Empa in Dübendorf getestet (siehe Abbildung 2). Die Probekörper bestanden entweder aus normalfestem Beton, hochfestem Beton oder faserbewehrtem Beton und waren mit geschweissten Leitern, Bügeln oder Doppelkopfankern kontinuierlich in Quer- und Längsrichtung über die gesamte Höhe bewehrt (siehe Abbildung 3). Die Proben wurden mit kleinen Stahlklötzen über eine durchgehende Länge von 450 mm und einer Breite von 140 mm bzw. 210 mm belastet, was einem Lastkonzentrationsverhältnis von 40% (= 140 mm / 350 mm) bzw. 60% (= 210 mm / 350 mm) entsprach. Alle Proben bis auf zwei wurden zentrisch belastet.


Aus der Versuchskampagne lassen sich die folgenden Schlussfolgerungen für streifenbelastete Stahlbetonblöcke ableiten:
- Höhere Bewehrungsmengen führen zu höheren Traglasten.
- In Querrichtung kann Bewehrung bis zu einem geometrischen Bewehrungsgehalt von 4% aktiviert werden.
- Geschweisste Leiterbewehrung zeigt ein ähnliches Tragverhalten wie Bügelbewehrung und Doppelkopfankerbewehrung.
- Proben mit Hybridbewehrung (konventionelle Bewehrung kombiniert mit Stahlfasern) weisen höhere Traglasten auf als Proben mit gleicher Menge an konventioneller Bewehrung.
- Die Traglast von streifenbelasteten Stahlbetonblöcken, normiert mit der Betonfestigkeit, nimmt mit höherer Betonfestigkeit ab.
- Ein kleineres Lastkonzentrationsverhältnis führt zu einer höheren maximalen Pressung qx,u,exp. Man beachte, dass trotz des Anstiegs der Spannung qx,u,exp bei verringerter Belastungsbreite die Höchstlast aufgrund der kleineren belasteten Fläche abnimmt.
Für weitere Details zur Versuchsreihe wird auf Morger und Kaufmann verwiesen.
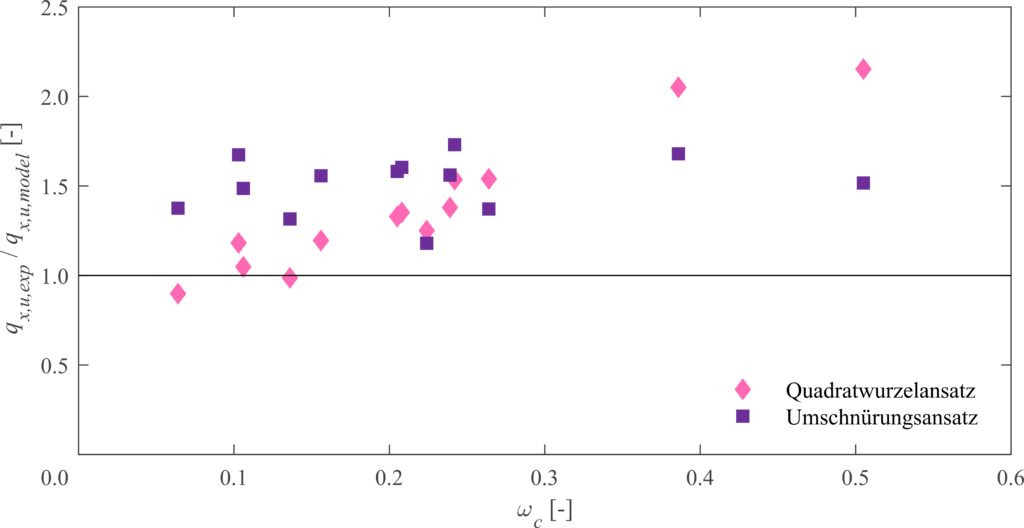
In Abbildung 4 ist das Verhältnis zwischen den experimentell gemessenen durchschnittlichen Pressungen beim Versagen qx,u,exp und den Vorhersagen der Bemessungsansätze qx,u,model gegen den mechanischen Bewehrungsgehalt ωc aufgetragen. Abbildung 4 zeigt nur die zentrisch belasteten Probekörper aus normal- und hochfestem Beton. Beim Quadratwurzelansatz ist zu erkennen, dass die Zuverlässigkeit der Vorhersagen mit zunehmendem Bewehrungsgrad abnimmt. Dabei ist zu beachten, dass die Bedingung der geometrischen Ähnlichkeit vernachlässigt wurde. Andernfalls resultierten wesentlich konservativere Vorhersagen. Mit dem Umschnürungsansatz wird der Einfluss unterschiedlicher Bewehrungsgehalte erfasst, jedoch wird die Tragfähigkeit der Versuchskörper unterschätzt, da der Einfluss der Lastausbreitung vernachlässigt wird.
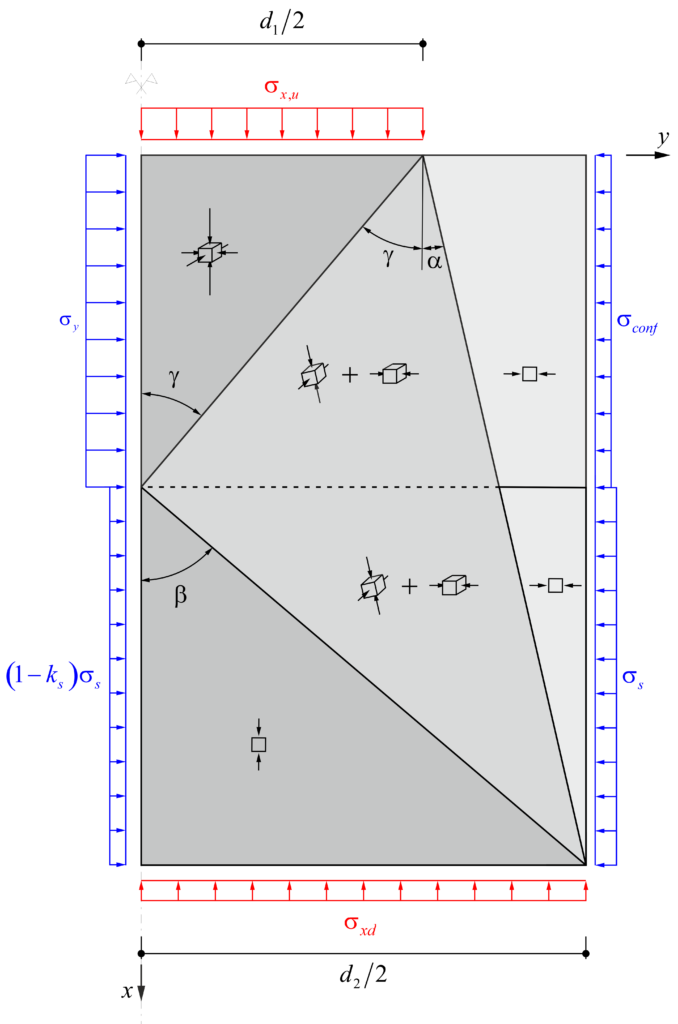
Das kürzlich publizierte mechanisch konsistente Dual-Wedge-Spannungsfeld (siehe Abbildung 5 oder Markic, Morger und Kaufmann) berücksichtigt sowohl die Lastausbreitung als auch die Umschnürungsbewehrung. Im Vergleich mit dem Quadratwurzel- und Umschnürungsansatz zeigt das Dual-Wedge-Spannungsfeld gute Übereinstimmung mit den Versuchen an streifenbelasteten Stahlbetonblöcken. Der detaillierte Vergleich des Dual-Wedge-Spannungsfeld mit den Experimenten wird in einer zukünftigen Publikation präsentiert.
Der fünfte Betontag wurde kürzlich an der Hochschule für Technik und Architektur Fribourg HTA-FR durchgeführt. Zu diesem Anlass widmet sich der aktuelle Blogpost der Schweizer Delegation der Fédération internationale du béton (fib-CH). In einem Interview haben wir uns mit Herrn Thierry Delémont, dem Delegationsleiter der fib-CH, und Herrn Dr. Patrick Valeri, seit kurzem Delegationsmitglied und Vorsteher der fib-CH Young Members Group, unterhalten. Sie stellen uns die Organisation, ihre Aufgaben und Ziele vor.
Das Comité Européen du Béton (CEB) und die Fédération Internationale de la Précontrainte (fip) schlossen sich 1998 zur heutigen Fédération internationale du béton (fib) zusammen. Das CEB, gegründet 1953 mit dem Ziel der Vereinheitlichung der Bestimmungen im Bauwesen auf europäischer Ebene, publizierte 1964 ihre ersten Empfehlungen für ein Normenwerk. In Zusammenarbeit mit der fip folgte dann 1978 die Publikation «International System of Unified Standard Codes of Practice for Structure», welche später die Grundlage für den Eurocode für Stahlbetonbauten bildete. Seit 1985 liegt der Sitz des CEB (und der heutigen fib) an der EPF Lausanne.
Was ist die Rolle der Schweizer Gruppe (fib-CH) innerhalb der fib?
Thierry Delémont: Die Schweiz hat bei der Gründung des CEB und der fib eine führende Rolle gespielt. In dieser Funktion bleibt sie trotz der Kleinheit unseres Landes ein wichtiger Akteur in der Organisation. Die strategischen Entscheidungen des fib werden jährlich im “Technical Council” und an der “General Assembly” getroffen. Mit drei Delegierten ist die Schweiz eines der am stärksten vertretenen Länder. Die fib-CH will die Ziele der fib auf nationaler Ebene vorantreiben: Förderung der Forschung im Bereich Betonbau, Verbreitung von Forschungs- und Entwicklungsergebnissen, Organisation von Kongressen, Symposien und Workshops, Erarbeitung von Empfehlungen auf nationaler und internationaler Ebene, Information der Mitglieder über die neusten Entwicklungen.
Unser Ziel ist es, eine Verbindung zwischen Berufseinsteigern und erfahrenen Ingenieur:innen herzustellen, damit die junge Generation auch eine aktive Rolle im Verband spielen kann.
Herr Valeri, Sie sind der fib während Ihres Doktorats beigetreten und haben da den Vorsitz der Schweizer fib Young Members Group (YMG) übernommen. Was ist die Funktion der YMG? Wer kann Mitglied werden? Hat sie ihre eigene Agenda und Ziele mit eigenen Prioritäten gegenüber dem Rest der fib?
Patrick Valeri: Die Kerninteressen der YMG sind der Wissenstransfer, das Networking, die Unterstützung der Task-Groups und die Organisation von Symposien. Unser Ziel ist es, eine Verbindung zwischen Berufseinsteigern und erfahrenen Ingenieur:innen herzustellen, damit die junge Generation auch eine aktive Rolle im Verband spielen kann. Laut Tomaž Ulaga, Mitglied der Schweizer Delegation, war es vor einigen Jahrzehnten Tradition, dass jeder Ingenieur / jede Ingenieurin Mitglied von mindestens einem Fachverband war. Heutzutage nimmt der hektische Berufsalltag sehr viel Zeit in Anspruch, und die Zahl der Verbandsmitglieder verringert sich stetig. Die YMG versucht diesem Trend entgegenzusteuern.

Am 25. Oktober 2022 fand an der Hochschule für Technik und Architektur in Fribourg der fünfte fib-CH Betontag statt. Seit wann wird dieser durchgeführt? An wen ist er gerichtet und welche Ziele hat er?
Thierry Delémont: Das Hauptziel ist es, mit der Publikation Betonbau in der Schweiz, das Know-how der Schweizer Ingenieure der internationalen Ingenieurgemeinschaft vorzustellen. Dies, trotz des Fakts, dass nur sehr wenige Schweizer Ingenieure ihre Projekte an den fib-Kongressen vorstellen. In einem zweiten Schritt wird mit dem Betontag ein regelmässig stattfindender Anlass geschaffen, an dem sich die Akteure der Branche treffen und austauschen können.
Patrick Valeri: Die Publikation erscheint im Vierjahrestakt, sprich im selben Rythmus wie der fib-Kongress, welcher ebenfalls alle vier Jahre stattfindet. Zudem stellt der Betontag eine Verbindung der Schweizer Delegation der fib mit der fib-International her und erhält sie aufrecht.
Eine Auswahl der wichtigsten Betonbauprojekte wird in der Publikation Betonbau in der Schweiz vorgestellt und am folgenden Betontag präsentiert. Eine der ersten Schweizer Publikationen, Spannbeton in der Schweiz, kam als Sammlung Schweizer Beiträge vom siebten fip Kongress 1974 zustande. In dieser Publikation ist ein Beitrag zum Entwurf und Bau des Viadukts über die Paudèze zu finden, und in der diesjährigen Ausgabe wurde die Erweiterung und Sanierung des Bauwerks vorgestellt. Der Betontag und die Publikationen tragen so zu einer Baukultur mit hoher Qualität in der Schweiz und deren Aufrechterhaltung bei.

Welche Bedeutung hat dieser Betontag für Sie beide persönlich? Wieso nehmen Sie daran teil?
Thierry Delémont: Dieser Anlass ist immer eine gute Gelegenheit, Kollegen zu treffen, denen man nicht regelmässig begegnet, und neue Bekanntschaften zu schliessen. Es bietet auch die Möglichkeit, Projekte aus anderen Regionen der Schweiz zu entdecken, von denen man sonst nicht hören würde. Ich hatte die Gelegenheit, bei einer früheren Veranstaltung ein Projekt vorzustellen, doch heute nehme ich als Organisator teil.
Patrick Valeri: Der Betontag hat für mich verschiedene Funktionen. Zum einen, ist er eine Drehscheibe, um neue Verbindungen zu knüpfen und bestehende Bekanntschaften aufrecht zu erhalten und zu pflegen. Idealerweise treffen sich hier Planer, Unternehmer, Bauherren und Studierende, um sich informell austauschen zu können. Dieser Austausch fördert Innovation und Qualität in der Projektierung und bei der Realisierung. Zum anderen können wir uns auch von den Vorträgen inspirieren lassen, wobei wir einen Überblick bekommen, wo wir als Gesellschaft gerade hinsteuern, und an welchen Themen wir noch arbeiten müssen.
Wie hat sich die fib-CH Gruppe und die Schweizer BauIngenieur:innen-Gesellschaft im Allgemeinen über die letzten paar Jahrzehnte hinweg entwickelt? Und wohin will man sich weiterentwickeln?
Thierry Delémont: Aus persönlicher Sicht bedauere ich, dass die Mehrheit der praktizierenden Bauingenieur:innen in der Schweiz nicht besonders daran interessiert ist, sich über Verbände wie die fib am internationalen Austausch zu beteiligen. Wahrscheinlich ermutigt die privilegierte Situation der Schweiz die Ingenieur:innen nicht, sich im Ausland zu engagieren. Im Gegensatz dazu sind die beiden technischen Hochschulen und einige Fachhochschulen sehr aktiv, was auf die Initiative ihrer Professor:innen zurückzuführen ist, die viel stärker für die Bedeutung des internationalen Austauschs sensibilisiert sind. Es wäre daher wünschenswert in Zukunft mehr praktizierende Bauingenieur:innen aus der Schweiz davon zu überzeugen, sich in fib-Arbeitsgruppen zu engagieren, da sie dort nicht nur viel beitragen, sondern auch viel lernen können.
Wo sehen Sie noch Verbesserungspotenzial im Austausch und in der Zusammenarbeit auf internationaler Ebene und zwischen Industrie und Forschung?
Patrick Valeri: Durch die Digitalisierung haben wir in den letzten Jahrzehnten eine allgemeine Beschleunigung unserer Gesellschaft erlebt. In meinen Augen kann dies, unter Umständern zu einer Spaltung zwischen Forschung und Praxis führen, denn Normen, Richtlinien und marktreife Produkte können nicht immer auf dem letzten Stand des Wissens sein. Hinzu kommt, dass in der Praxis (Projektierung, Produktherstellung) und Forschung nicht immer die gleichen Ziele verfolgt werden – weil hier andere Markt- und Finanzkräfte im Spiel sind.
Die fib-International besteht aus Hochschulprofessor:innen und Ingenieur:innen die in Forschung, Projektierung und Produktentwicklung tätig sind. Die Zusammenarbeit dieser Leute, die sich an einen gemeinsamen Tisch setzen, versucht, der Spaltung von Forschung und Praxis entgegenzusteuern. Dazu haben wir zwei Mechanismen: zum Einen können neue Forschungsarbeiten auf die Praxisanforderungen und Markterwartungen zugeschnitten werden. Und zum Anderen kann die Vielzahl an wissenschaftlichen Publikationen in praxistaugliche Richtlinien transformiert werden (fib Bulletins). In diesem Sinne bildet die fib einen internationalen Arbeitsrahmen, damit Forschung und Praxis synergetisch zusammenarbeiten können.
Wir leben in einer globalisierten Welt mit Problemen, die den ganzen Planeten betreffen. Auch die Lösungen müssen auf globaler Ebene gedacht werden, und es wird immer wichtiger, Kontakte mit der gesamten internationalen Gemeinschaft der Ingenieure zu fördern, z.B. durch Verbände wie die fib.
Meine Kolleg:innen nehmen dieses Jahr zum ersten Mal am Betontag teil. Das ist für einige von Ihnen der erste Kontakt mit der fib. Wie wichtig ist es, dass sich vor allem jüngere Ingenieur:innen aktiv engagieren?
Patrick Valeri: Aus miener Sicht ist es aus mindestens zwei Blickwinkeln wichtig ist, dass sich die junge Generation aktiv in einem Verband engagiert. Erstens wird die bestehende Generation in Zukunft kürzer treten und in den Ruhestand gehen. Je früher wir als junge Ingenieure einem Verband beitreten, desto länger können wir diese Transitionsphase ausdehnen – und in dieser Zeit viel voneinander lernen. Zum Zweiten ist Verbandsarbeit auch mehr oder weniger das Gegenteil von unserem beruflichen Alltag, wo Projekte abgewickelt und abgeschlossen werden. In der fib, wie auch in anderen Fachverbänden, können wir unser Projektwissen in einem strukturierten Rahmen mit unseren Kolleg:innen teilen, um künftig davon zu profitieren. In diesem Sinne ist unsere Arbeit für einen Verband projektübergreifend und eine inspirierende Abwechslung zum Projektalltag.
Thierry Delémont: Wir leben in einer globalisierten Welt mit Problemen, die den ganzen Planeten betreffen. Auch die Lösungen müssen auf globaler Ebene gedacht werden, und es wird immer wichtiger, Kontakte mit der gesamten internationalen Gemeinschaft der Ingenieure zu fördern, z.B. durch Verbände wie die fib. Deshalb bietet die YMG jungen Ingenieur:innen eine hervorragende Möglichkeit, sich mit Kolleg:innen aus verschiedenen Ländern auszutauschen und gleichzeitig Vorschläge zu machen, die von der gesamten fib gehört werden.
Ein letztes Thema würde ich gerne noch ansprechen – es ist eins das mich persönlich stark beschäftigt: die Nachhaltigkeit in der Baubranche. Die Baubranche hat einen enormen CO2-Fussabdruck. Gemäss dem Bundesamt für Umwelt (BAFU) haben alleine die Treibhausgasemissionen der Zementherstellung einen Anteil von 35 % an den Industrieemissionen – dies entspricht rund 8.7 % der Schweizer Gesamtemissionen (Stand 2020, BAFU). Prof. Muttoni hat die Dringlichkeit im Schlusswort am Betontag deutlich zum Ausdruck gebracht. Was haben Sie von diesem Schlusswort mitgenommen und was würden Sie gerne mit der Leserschaft hier teilen?
Patrick Valeri: Es ist ein Thema, das uns alle betrifft und bewegen sollte. Im Kern appelliert Prof. Muttoni an uns Bauingenieure, Ressourcen intelligent zu nutzen und innovativ zu sein. Eines seiner genannten Beispiele waren Decken: ein Deckensystem aus Stahlbeton mit niedrigem Zementgehalt, mit bedachter Wahl der Zementart, statisch sinnvoller Geometrieführung und recycelten Baustoffen, insbesondere des Betonstahls, hat einen vergleichbaren CO2 –Fussabdruck wie eine Holzdecke. Mit Optimierungen kann man durchaus 80% kg CO2-Äquivalent einsparen, was beträchtlich ist. Holztragwerke liegen auch voll im Trend. Man soll dabei aber nicht vergessen, dass Holz begrenzt verfügbar ist und in seiner Funktion den Beton nicht ersetzen kann. Das ist der Fall bei den meisten Strassen- und Bahnbrücken, Stützbauwerken, Erdbebenaussteifungen von Hochhäusern und dergleichen, um nur wenige Beispiele zu nennen. Dennoch, der Trend hin zu hybriden Stahlbeton-Holztragwerken im Hochbau ist erfreulich. Die fib selbst unterstützt diesen Trend aktiv: am Conceptual Design Symposium 2021 in Attisholz wurden mehrere Beiträge zum Entwurf von Holz- Betonhybridbauwerken vorgetragen, wie beispielweise der Holliger Tower präsentiert von Dr. Neven Kostić (siehe Video).
Was vom Schlusswort auf jeden Fall auch nachhallen sollte, sind die Gesamtleistungswettbewerbe als Mittel für mehr Nachhaltigkeit. Sie bieten sich als Methode zur Projektoptimierung an, und bieten Raum für Innovation und Materialeinsparungen. Wichtig wäre, dass in ihnen auch die Ökobilanz bewertet und berücksichtig würde. In diesem Sinne müssen aber alle Involvierten, also die Bauherren, Ingenieure, Bauunternehmer und Zementhersteller auf ein nachhaltigeres Ziel, sowie innovative und effiziente Lösungen hinarbeiten.
Tena Galkovski
Zu den Interviewen:
Thierry Delémont
Ing. Civ. Dipl. EPF / SIA
Delegationsleiter fib-CH
Managing director at T ingénierie sa
Dr. Patrick Valeri
MSc ing. civile PoliMi / SIA
Delegationsmitglied fib-CH
fib YMG-CH Vorsteher
Projektleiter Dr. Lüchinger+Meyer Bauingenieure AG
Link to the English version: The formwork as a major challenge in the fabrication of efficient, economical and sustainable concrete slabs
Die aktuelle Umweltkrise verlangt nach dem Bau von nachhaltigeren Tragwerken, was einen radikalen Wandel in der Art und Weise, wie wir heute planen und bauen erfordert [1]. Veränderungen in der Bauindustrie gehen im Vergleich zu anderen Branchen wie der Automobil- oder Computerindustrie traditionell langsam vonstatten. Trotzdem besteht (zumindest) in der Wissenschaft bereits ein allgemeines Einvernehmen darüber, dass Baumaterialien und Tragwerke reduziert, wiederverwendet, rezykliert und wiedergewonnen werden müssen, um eine radikale Senkung der CO2-Emissionen einer Branche zu erreichen, die für 38 % der weltweiten Treibhausgasemissionen verantwortlich ist [2][3].
Forschungsgruppen unternehmen erhebliche Anstrengungen, um die Tragwerkseffizienz und die Herstellung von Betondecken zu optimieren und den Materialverbrauch zu verringern, da diese Elemente im Allgemeinen zwischen 40 % und 60 % des Betons in der Gebäudestruktur ausmachen [4]. Ausserdem übertragen leichtere Decken geringere Lasten auf die vertikale Tragstruktur, was geringere Abmessungen von Stützen, Wänden und Fundamenten ermöglichen kann.
Tragwerkseffizienz wird durch Optimierung der Form, Topologie und Abmessungen angestrebt, was zu dünnschaligen Betondecken verschiedener Art [5][6], Rippendecken [7][8] oder einer Kombination von beidem [9][10][11] führt. Modernste Methoden und Softwares ermöglichen Deckensysteme mit einem Höchstmass an Optimierung des Tragwerkes. Trotz innovativer Anwendungen der digitalen Fertigung gibt es bei der Konstruktion dieser meist komplexen Formen immer noch Schwierigkeiten in Bezug auf Nachhaltigkeit und Wirtschaftlichkeit. Während die erste Anforderung in der Regel selbst auferlegt ist, bis strengere Nachhaltigkeitsvorschriften eingeführt werden, erinnert die raue Wirklichkeit der Bauindustrie Forscher:innen, die ihre Innovationen verbreiten wollen, daran, dass ein wirtschaftlich nicht rentables System nur sehr geringe Chancen hat, auf dem Massenmarkt Fuss zu fassen und somit einen Einfluss auf die Gesellschaft zu haben. Eine der grössten Herausforderungen in diesem Zusammenhang ist die Herstellung der Schalung.*
Ein Blick in die Vergangenheit verdeutlicht die Bedeutung wirtschaftlicher Schalungen für den Bau nicht geradliniger Elemente, allen voran Gewölbe und Schalen. Alte, grosse Baumeister:innen, Architekt:innen oder Ingenieur:innen verliessen sich auf eine bestimmte wirtschaftliche Art der Herstellung oder Verwendung der Schalung, um ihre Mauerwerke oder Betonschalen bauen zu können, oder sie griffen in einigen Fällen sogar auf Techniken zurück, die keine Schalung erforderten. Einige Beispiele für die zahlreichen existierenden Techniken werden in den folgenden Abschnitten vorgestellt. Nach ihrer Emigration aus Spanien im Jahr 1881 errichteten die Guastavinos (Rafael Guastavino Sr. und sein Sohn) in den Vereinigten Staaten rund 1000 Gebäude dank einer wirtschaftlichen, ausdrucksstarken und feuerfesten Bautechnik: dem Ziegelgewölbe [12]. Ziegelgewölbe (manchmal auch als Timbrel, katalanische Gewölbe oder Guastavino-Gewölbe bezeichnet) sind Mauerwerkskonstruktionen aus dünnen Ziegeln (Fliesen), Mörtel und schnell abbindendem Zement oder Gips. Die Ziegel werden flach verlegt und bilden zwei, drei oder mehr Schichten. Traditionell werden Ziegel wegen ihres geringen Gewichts verwendet, was zusammen mit der Verwendung eines schnell abbindenden Bindemittels eine notwendige Voraussetzung für den Bau der ersten Schicht ohne Stützschalung ist [13] [14] [15] (Abbildung 1).

Auch der Ingenieur Eduardo Torroja (1899-1961) nutzte diese Bautechnik, denn ” such shells [tile vaults] are cheap to make and may be adapted to any desired shape, even to continuously changing curvatures, […]. If constructed by bricklayers skilled in the technique, they can be made without the aid of formwork..” [16]. Er verwendete sie in Kombination mit Bewehrung beispielsweise bei einer Kirche in Pont de Suert (Abbildung 2) oder den Fundamenten der Sancti-Petri-Brücke in Cadiz, beide in Spanien [17] [18] [19].

Der italienische Ingenieur Pier Luigi Nervi (1891-1979) unternahm ebenfalls grosse Anstrengungen, um durch geeignete Schalungssysteme wirtschaftliche Bauweisen zu erzielen. Die Suche nach einer Möglichkeit, massive Holzschalungen, wie er sie bei einigen seiner ersten Hangars für die italienische Luftwaffe verwendete, zu vermeiden, führte ihn zur Verwendung von vorgefertigten Betonelementen und wiederverwendbaren Schalungen aus Ferrozement auf beweglichen Gerüsten [20].
Wiederverwendbare und bewegliche Schalungen wurden auch von dem uruguayischen Ingenieur Eladio Dieste (1917-2000) verwendet [21]. Diese Tatsache hat einen ausserordentlichen Einfluss auf das Design seiner verstärkten Ziegelschalen, die einen sich wiederholenden Rhythmus der gleichen Form entlang der Länge des Gebäudes aufweisen (Abbildung 3). Die Menge und Art des Mörtels in den Fugen der Ziegelsteine ermöglichte ein schnelles Entfernen der Schalung, um sie so schnell wie möglich für den nächsten Teil des Gebäudes zu verwenden [22] [23].

Der spanische Architekt Félix Candela (1910-1997) erzielte wirtschaftliche Schalungen für seine Betonschalen, indem er seine Tragwerke als hyperbolische Paraboloide formte. Solche Regelflächen ermöglichten eine einfache und schnelle Konstruktion der Schalung, bei der nur wiederverwendbare, gerade Holzbretter verwendet wurden. Dieses System in Verbindung mit den relativ niedrigen damaligen lokalen Lohnkosten ermöglichte ihm eine erfolgreiche Karriere im Bau von dünnwandigen Betonschalenkonstruktionen [25].
Hyperbolische Paraboloide wurden auch von Antoni Gaudí (1852-1926) und Luis Moya (1904-1990) als Ziegelgewölbe gebaut. Gaudí verwendete diese Form für die Ziegelgewölbe der Vorhalle der Kirche der Colonia Güell in Santa Coloma de Cervelló, Spanien [26]. Anschliessend goss er Beton auf das als integrierte Schalung fungierende Ziegelgewölbe, um ein hybrides Tragwerk aus Mauerwerk und Beton zu schaffen [19]. Der Architekt Luis Moya verwendete ein hyperbolisches Paraboloid zur Überdachung der Kapelle, die er für die Schule Santa María del Pilar in Madrid, Spanien, entwarf [27]. Bei diesem Dach handelt es sich um ein 743 m2 grosses, 14 cm dickes, bewehrtes Ziegelgewölbe, das auf einem Traggerüst aus Holzbrettern mit einem Abstand von 60 cm errichtet wurde. Die Bewehrung befindet sich zwischen den Ziegelschichten, während auf dem Mauerwerk eine 10 cm dicke Schicht aus Leichtbeton aufgebracht ist [28] (Abbildung 4).

Die Möglichkeit der Verwendung von Ziegelgewölben als integrierte Schalung für Beton wurde durch den Autor dieser Zeilen untersucht [29]. In der Forschung zu diesem Thema wird diese Bautechnik als eine Möglichkeit vorgestellt, ausdrucksstarke Stahlbetonschalen (einschliesslich Deckensystemen) unter Verwendung von Ziegelgewölben als integrierter Schalung zu bauen, mit dem Ziel, die Kosten und den Materialabfall zu reduzieren und gleichzeitig einen einzigartige Oberfläche auf der inneren Gewölbefläche zu schaffen [30] (Abbildung 5). Die Baukosten können vor allem aufgrund der niedrigen Materialkosten und der Tatsache, dass keine zusätzlichen Schalungen oder Fundamente erforderlich sind, gesenkt werden.

Zur Validierung dieser Konstruktionstechnik wurden experimentelle Untersuchungen, einschliesslich Belastungstests an Materialproben und Prototypen in Originalgrösse, durchgeführt, wobei es sich um die ersten Labortests für diese Art von Verbundtragwerken handelte [31] [32] (Abbildung 6). Die Kalibrierung der Finite-Elemente-Modelle auf der Grundlage der Versuchsergebnisse ermöglichte die Definition einer zuverlässigen Modellierungstechnik, eines Materialmodells und Materialeigenschaften für die Analyse dieser Art von Tragwerken. Darüber hinaus wurde eine auf der Grenzwertanalyse [33] basierende Methode beschrieben, um solche einfach gekrümmten Tragwerke sicher zu entwerfen und ihre Festigkeit und Stabilität gegenüber äusseren Belastungen zu bewerten. Die Methode wurde Extended Limit Analysis of Reinforced Masonry (ELARM) genannt, geht auf Roca et al. [34] zurück und liefert grafische und intuitive Ergebnisse in 2D [30]. Ein dreidimensionaler Ansatz von ELARM wurde ebenfalls vorgestellt [35].

Statische Analysemethoden, experimentelle Forschung und Entwurfsmethoden wurden für diese Bautechnik erfolgreich bereitgestellt. Dies reicht jedoch nicht aus, um den Sprung auf den Massenmarkt zu schaffen. Die Bewertung der Rentabilität dieser Technik hängt stark von der Form, der Spannweite und der Anzahl der Wiederholungen dieser Form ab. Ausserdem sind die Baukosten variabel und hängen von vielen Faktoren ab, wobei der Standort ein wichtiger Faktor ist. Was das Hauptthema dieses Beitrags betrifft, d. h. die Verwendung der vorgestellten Technik für Deckensysteme mit kleiner oder mittlerer Spannweite, so könnte sie dort rentabel und wettbewerbsfähig sein, wo die Arbeitskräfte im Baugewerbe nicht teuer sind.
Das Gleichgewicht zwischen Nachhaltigkeit und Wirtschaftlichkeit bei der Herstellung von optimierten Decken zu finden, ist eine der Herausforderungen der dritten Phase des Nationalen Forschungsschwerpunkts Digitale Fabrikation (NCCR dfab) der ETH Zürich. Einerseits müssen sich die Forschenden mit der Nachhaltigkeit befassen, mit dem Fokus auf Material- und Abfallreduktion, dem Einsatz von Materialien mit geringerem CO2-Fussabdruck, zirkulärem Bauen und Wiederverwendungsmöglichkeiten. Andererseits sollen wirtschaftliche Systeme geschaffen werden, die es den entwickelten Ideen, Konzepten und Patenten ermöglichen, den Massenmarkt zu erreichen, um einen grundlegenden Wandel in der Bauindustrie zu bewirken.
Wie bereits erwähnt, sind Lösungen kontextabhängig. Lokale Ressourcen, Materialien, Traditionen und Fachwissen tragen dazu bei, dass ein System in verschiedenen Teilen der Welt erfolgreich ist oder scheitert. Um eine relevante, globale Umweltwirkung zu erzielen, sollte daher besonderes Augenmerk auf die Umsetzung der Innovationen in den Regionen gelegt werden, in denen in den nächsten Jahrzehnten umfangreiche Bauvorhaben stattfinden werden.
*In diesem Beitrag werden mit dem Begriff “Schalung” teilweise auch die die Schalung stützenden Elemente im Sinne von Gerüsten oder Lehrgerüsten mitgemeint.
[1] Block P, Van Mele T, Rippmann M, Ranaudo F, Calvo Barentin C, Paulson N. Redefining Structural Art: Strategies, necessities and opportunities. The Structural Engineer 2020;98:66–72.
[2] Mai I, Brohmann L, Freund N, Gantner S, Kloft H, Lowke D, et al. Large Particle 3D Concrete Printing—A Green and Viable Solution. Materials 2021;14:6125. https://doi.org/10.3390/ma14206125.
[3] Agustí-Juan I, Habert G. Environmental design guidelines for digital fabrication. Journal of Cleaner Production 2017;142:2780–91. https://doi.org/10.1016/j.jclepro.2016.10.190.
[4] Bischof P, Mata-Falcón J, Kaufmann W. Fostering innovative and sustainable mass-market construction using digital fabrication with concrete. Cement and Concrete Research 2022;161:106948. https://doi.org/10.1016/j.cemconres.2022.106948.
[5] Hawkins W, Orr J, Shepherd P, Ibell T. Design, Construction and Testing of a Low Carbon Thin-Shell Concrete Flooring System. Structures 2019;18:60–71. https://doi.org/10.1016/j.istruc.2018.10.006.
[6] Hawkins W, Orr J, Ibell T, Shepherd P. A design methodology to reduce the embodied carbon of concrete buildings using thin-shell floors. Engineering Structures 2020;207:110195. https://doi.org/10.1016/j.engstruct.2020.110195.
[7] Mata-Falcón J, Bischof P, Huber T, Anton A, Burger J, Ranaudo F, et al. Digitally fabricated ribbed concrete floor slabs: a sustainable solution for construction. RILEM Tech Lett 2022;7:68–78. https://doi.org/10.21809/rilemtechlett.2022.161.
[8] Burger J, Huber T, Mata-Falcón J, Lloret Fritschi E, Kaufmann W, Gramazio F, et al. Design, fabrication, and testing of an optimised reinforced concrete floor slab fabricated with robotically 3D printed formwork (accepted). Third RILEM International Conference on Concrete and Digital Fabrication, 2022.
[9] López López D, Veenendaal D, Akbarzadeh M, Block P. Prototype of an ultra-thin, concrete vaulted floor system. Proceedings of IASS Annual Symposia 2014;2014:1–8.
[10] Liew A, López López D, Van Mele T, Block P. Design, fabrication and testing of a prototype, thin-vaulted, unreinforced concrete floor. Engineering Structures 2017;137:323–35. https://doi.org/10.1016/j.engstruct.2017.01.075.
[11] Nuh M, Oval R, Orr J, Shepherd P. Digital fabrication of ribbed concrete shells using automated robotic concrete spraying. Additive Manufacturing 2022:103159. https://doi.org/10.1016/j.addma.2022.103159.
[12] Ochsendorf J. Guastavino Vaulting: The Art of Structural Tile. Reprint edition. New York: Princeton Architectural Press; 2013.
[13] Truñó A. Construcción de bóvedas tabicadas. 1st edition. Madrid: INSTITUTO JUAN DE HERRERA; 2004.
[14] López López D, Domènech Rodríguez M, Palumbo Fernández M. “Brick-topia”, the thin-tile vaulted pavilion. Case Studies in Structural Engineering 2014;2:33–40. https://doi.org/10.1016/j.csse.2014.09.001.
[15] López López D, Van Mele T, Block P. Tile vaulting in the 21st century. Informes de la Construcción 2016;68:e162–e162. https://doi.org/10.3989/ic.15.169.m15.
[16] Torroja Miret E. The structures of Eduardo Torroja: an autobiography of engineering accomplishment. New York: F.W. Dodge Corporation; 1958.
[17] Torroja Miret E. Memoria. No 19.301 1926.
[18] Torroja Miret E. Iglesia de Pont de Suert. Informes de la Construcción 1962;14:59–70. https://doi.org/10.3989/ic.1962.v14.i137.4933.
[19] López López D, Van Mele T, Block P. The combination of tile vaults with reinforcement and concrete. International Journal of Architectural Heritage 2019;13:782–98. https://doi.org/10.1080/15583058.2018.1476606.
[20] Halpern AB, Billington DP, Adriaenssens S. The Ribbed Floor Slab Systems of Pier Luigi Nervi n.d.:7.
[21] Anderson S. Eladio Dieste: Innovation in Structural Art. 1st edition. New York: Princeton Architectural Press; 2004.
[22] Dieste E, Arana M, Garabelli L. Diálogos con Dieste. SUMMA 1980;8:96–101.
[23] López López D, Van Mele T, Block P. Dieste, González Zuleta and Sánchez del Río: Three approaches to reinforced-brick shell structures. Structural Analysis of Historical Constructions: Anamnesis, Diagnosis, Therapy, Controls, CRC Press; 2016.
[24] Dieste E. Iglesia en Montevideo. Templo parroquial de Atlántida. Informes de la Construcción 1961;13:43–56. https://doi.org/10.3989/ic.1961.v13.i127.5106.
[25] Cassinello P, Schlaich M, Torroja JA. Félix Candela. In memorian (1910-1997). From thin concrete shells to the 21st century’s lightweight structures. Informes de la Construcción 2010;62:5–26. https://doi.org/10.3989/ic.10.040.
[26] González Moreno-Navarro JL, Casals Balagué A. Gaudí y la razón constructiva. Un legado inagotable. Akal; 2002.
[27] Moya Blanco L, Domínguez Salazar JA. Capilla del Colegio de Santa María del Pilar, Madrid. Informes de la Construcción 1965;18:49–61. https://doi.org/10.3989/ic.1965.v18.i173.4340.
[28] Moya Blanco L. Memoria descriptiva de construcción y material y mediciones del proyecto para la construcción de una capilla y cripta en el colegio Santa María del Pilar 1963.
[29] López López D. Tile Vaults as Integrated Formwork for Concrete Shells: Construction, Experimental Testing, Structural Analysis and Design. Doctoral Thesis. ETH Zurich, 2019. https://doi.org/10.3929/ethz-b-000417993.
[30] López López D, Roca P, Liew A, Van Mele T, Block P. Tile vaults as integrated formwork for reinforced concrete: Construction, experimental testing and a method for the design and analysis of two-dimensional structures. Engineering Structures 2019;188:233–48. https://doi.org/10.1016/j.engstruct.2019.03.034.
[31] López López D, Bernat-Maso E, Gil L, Roca P. Experimental testing of a composite structural system using tile vaults as integrated formwork for reinforced concrete. Construction and Building Materials 2021;300:123974. https://doi.org/10.1016/j.conbuildmat.2021.123974.
[32] López López D, Bernat-Maso E, Gil L, Roca P. Experimental testing of tile vaults. Brick and Block Masonry – From Historical to Sustainable Masonry, CRC Press; 2020.
[33] Heyman J. The stone skeleton. International Journal of Solids and Structures 1966;2:249–79.
[34] Roca P, López-Almansa F, Miquel J, Hanganu A. Limit analysis of reinforced masonry vaults. Engineering Structures 2007;29:431–9. https://doi.org/10.1016/j.engstruct.2006.05.009.
[35] López López D, Roca P, Liew A, Méndez Echenagucia T, Van Mele T, Block P. A three-dimensional approach to the Extended Limit Analysis of Reinforced Masonry. Structures 2022;35:1062–77. https://doi.org/10.1016/j.istruc.2021.06.013.
David López López
Comment on this post on LinkedIn or Instagram
Link to the English version: Finite-Element-Method in Structural Engineering
Grundprinzip und Anwendungsgebiete der FEM
Computerunterstützte Berechnungsmethoden – allen voran die Finite Elemente Methode (FEM) – haben sich in den letzten Jahrzehnten zu einem unverzichtbaren Werkzeug im Ingenieurwesen gemacht. Mit der Entwicklung der FEM können alltägliche Rechen- und Routineaufgaben automatisiert und ohne Flüchtigkeitsfehler durchgeführt werden. Damit ist (zumindest ein Teil) von Konrad Zuse’s [1] Traum von der Übernahme “lästiger” Aufgaben durch eine vollautomatisierte Rechenmaschine Wirklichkeit geworden. Die Aufgabe vom Ingenieur hat sich also vom Rechnen hin zur Modellbildung und Resultatinterpretation verlagert, für die jedoch die zugrundegelegten Theorien und Methoden bewusst und richtig angewendet werden müssen. Damit ist die Kunst der Baustatik nicht überflüssig geworden, sondern im Gegenteil, anspruchsvoller und interessanter.

Ganz allgemein gesprochen liefert die FEM eine numerische Näherungslösung für alle Aufgaben, die mathematisch mit partiellen Differentialgleichungen darstellbar sind, für die keine geschlossenen Lösungen vorliegen. Etwas vereinfachter ausgedrückt werden in der FEM komplexe Systeme (Tragwerke) in Komponenten (finite Elemente) aufgeteilt und mathematisch zu einem Gesamtmodell verknüpft. Sind die mechanischen Eigenschaften (Steifigkeiten) der einzelnen Elemente, durch eine im Rahmen der ausgewählten strukturmechanischen Modellierung vorgegebenen Beziehungen zwischen Spannungen und Verzerrungen bekannt, lassen sich unter gegebenen Einwirkungen und Randbedingungen (Lagerung) die Auswirkungen (z.B. Schnittkräfte, Verformungen, usw.) am Gesamtmodell ermitteln.
Für die alltäglichen Aufgaben der Bauingenieure/innen kommt meistens die linear-elastische FEM zum Einsatz, wobei ein linearer Zusammenhang zwischen den Spannungen und Verzerrungen vorausgesetzt wird. Die FEM liefert dabei z.B. die Schnittkräfte für die Bemessung eines Bauteils auf Basis von ideal-plastischen Modellvorstellungen. In Spezialfällen z.B. bei der statischen Überprüfung von bestehenden Tragwerken kommt immer öfters die (materielle [2]) nichtlineare FEM zur Anwendung. Dabei wird ein nichtlinearer Zusammenhang zwischen den Spannungen und Verzerrungen angesetzt, womit Aussagen zum Last-Verformungsverhalten, der Rissbildung und der damit einhergehenden Schnittkraftumlagerung möglich sind. Damit lassen sich gegenüber herkömmlichen Berechnungsmethoden Traglastreserven identifizieren und effizientere Tragwerke erstellten oder im Idealfall teure Verstärkungsmassnahmen bei der statischen Ertüchtigung verhindern. Ist die reine Anwendung solcher nichtlinearer FEM-Programme dank der Entwicklung von benutzerfreundlichen Oberflächen heutzutage relativ einfach, umso komplexer gestaltet sich die Frage um die Wahl der zur vorliegenden Problemstellung passenden (nichtlinearen) Material- und Strukturmodellierung. Die Modellvorstellungen und deren Grenzen sowie die Eigenheiten einer NLFE Berechnung (z.B. Divergenzen) sollten im Detail verstanden werden. Die Vermittlung dieses Wissens ist eine zentrale Herausforderung für uns als Lehr- und Forschungsinstitut.
Geschichtlicher Abriss der Finite Elemente Methode
Im Allgemeinen geht die Entwicklung der FEM nicht auf eine einzige Person oder ein einzelnes Fachgebiet zurück, sondern hat bis heute einen stark interdisziplinären Charakter mit Aspekten aus der Mathematik, der Mechanik, dem Ingenieurwesen und der Informatik. Die Entwicklung der FEM begann in den 1950er Jahren und wurde durch die Pionierarbeiten von J. Argyris an der Universität Stuttgart, R.L. Taylor oder R. Clough an der Universität von Kalifornien, Berkley und O.C. Zienkiewicz von der Universität von Wales geprägt (alles ausgebildete Bauingenieure!). Ab den 1960er Jahren nahm die Entwicklung mit der ersten internationalen FEM Konferenz 1965 und mit dem ersten Standardwerk 1967 von Zienkiewicz mit dem Titel “The Finite Element Method in Structural and Continuum Mechanics” richtig Fahrt auf.

Die Anwendung der FEM auf Stahlbetonstrukturen begann Ende der 1960er mit den Arbeiten von Ngeo and Scordelis 1967 and Rashid 1968. Seit daher wurden unzählige Publikationen und Bücher mit den theoretischen Grundlagen, Anwendungsfällen und Richtlinien publiziert (siehe FIB Bulletin 45 2008). Die ersten FEM-Programme wurden an Universitäten entwickelt und ab den 1970er zu kommerziellen FE-Paketen mit erhöhter Benutzerfreundlichkeit weiterentwickelt (Ansys, Abaqus, ATENA, Diana). Dabei entstanden eine Vielzahl von verschieden Elementtypen (1D bis 3D) und diverse mathematische Lösungsalgorithmen für die Orts- und Zeitdiskretisierung des vorliegenden Problems. Eine Vorreiterrolle in der Entwicklung von nichtlinearen Materialmodellen für Stahlbeton und deren Implementierung in entsprechende FEM-Programme nahmen dabei D. Mitchel, M.P. Collins und F. J. Vecchio von der Universität in Toronto in den 1980er Jahren ein (Entwicklung der Druckfeldmodelle und deren Implementierung in die Software VecTor). Heutzutage ist die FEM eines der am meist verbreiteten numerischen Lösungsverfahren für unterschiedlichste physikalische Aufgabenstellungen im Bereich aller Ingenieurswissenschaften bis hin zu Wettervorhersagen. Desto stolzer können wir sein, dass Bauingenieure einen signifikanten Beitrag bei der Entwicklung der FEM lieferten.
NLFE-Tools an der Professur für Massiv- und Brückenbau
Wir von der Professur für Massiv- und Brückenbau konzentrieren uns auf die Entwicklung von nichtlinearen Materialmodellen und deren Implementierung in numerische Methoden, wie eben der FEM. In den letzten Jahren wurden an der Professur für Massiv- und Brückenbau verschiedene Tools zur nichtlinearen FEM Analyse von Bauteilen aus Stahlbeton und Mauerwerk entwickelt:
Die Compatiable Stress Field Method (CSFM) eignet sich für die detaillierte Analyse von einzelnen, eben beanspruchten Stahlbetonbauteilen eines Gesamttragwerkes (z.B. Rahmenecken oder Längsträger einer Hohlkastenbrücken wie in Abbildung 3 ersichtlich). Das CSFM basiert im Wesentlichen auf der Implementierung des Zuggurtmodelles in das FE-Programm Idea StatiCa Detail.
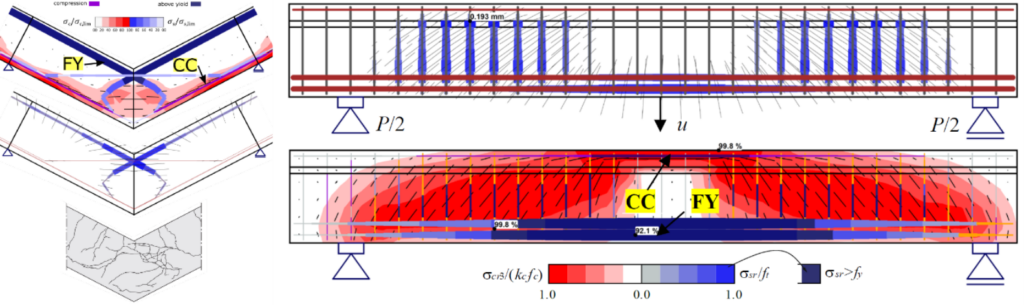
Das CMM-Usermat beinhaltet im Wesentlichen die Implementierung des durch Prof. Dr. Walter Kaufmann entwickelten Cracked Membrane Model (gerissenes Scheibenmodell) als user-defined material (Usermat) in das FEM-Programm ANSYS Mechanical APDL. In Kombination mit dem Schichtenmodell lassen sich damit komplexe Schalentragwerke (kombinierte Platten- und Scheibentragwirkung) aus Stahlbeton untersuchen (siehe Abbildung 4).
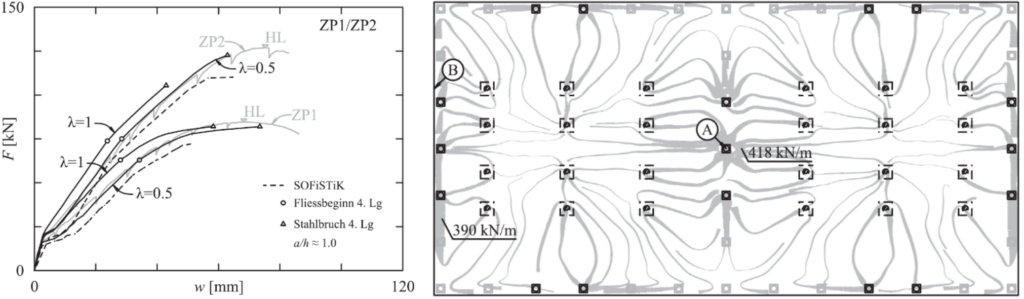
Mit dem URM-Usermat lässt sich das nichtlineare Tragverhalten von unbewehrten Mauerwerksstrukturen untersuchen (siehe Abbildung 5). Das URM-Usermat basiert auf der Implementierung erweiterter Bruchbedingungen von Ganz (welche in den 1980er an der ETH Zürich entwickelt und heute immer noch als Grundlage für die Bemessung von Mauerwerk verwendet werden) als user-defined material in das FEM-Programm ANSYS Mechanical APDL. In Kombination mit dem CMM-Usermat lässt sich das komplexe Tragverhalten von Mischtragwerken aus Stahlbeton und Mauerwerk untersuchen (siehe Abbildung 6).
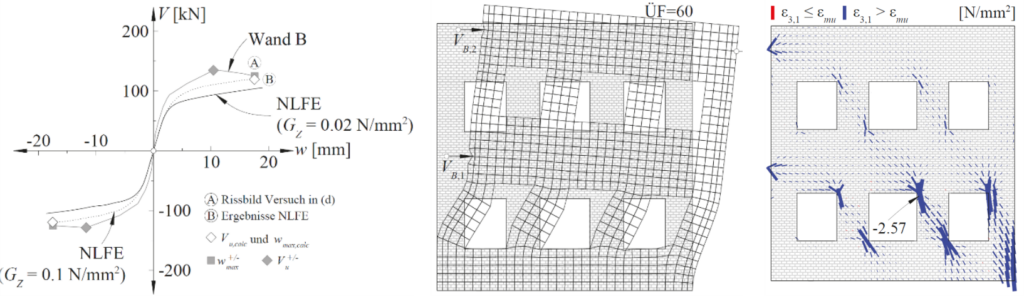
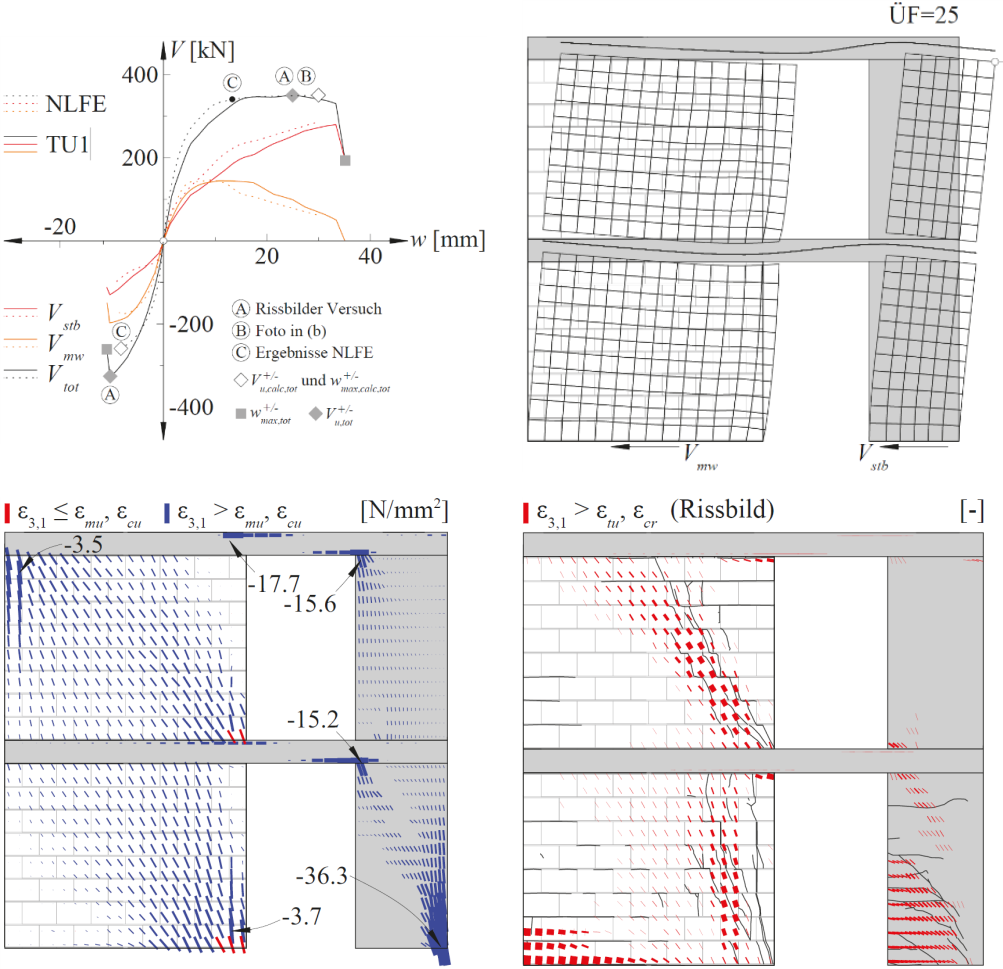
Allen NLFE-Tools gemeinsam ist, dass die Materialmodelle – auf Basis von mechanisch konsistenten Zusammenhängen – die wesentlichen Eigenschaften des Tragverhaltens von Stahlbeton bzw. Mauerwerk berücksichtigen. Zudem werden nur wenige, physikalisch klar definierte Inputparameter benötigt, welche bei der Bemessung oder der statischen Beurteilung von Tragwerken bekannt sind. Damit eignen sich die NLFE-Tools hervorragend für die Anwendung in der Baupraxis.
Aktuelle Entwicklungen
Die NLFE-Tools werden aktuell in die StrucEng Library implementiert, welche an der Professur für Massiv- und Brückenbau entwickelte wird. Die StrucEng Library ist eine OpenSource Software, mit welcher computergestützte Berechnungen von Tragsystemen aus Stahlbeton und Mauerwerk durchgeführt werden können. Dabei stehen neben den nichtlinearen Materialmodellen verschiedene weitere Materialmodelle zur Verfügung, welche das gesamte Spektrum vom Tragwerksentwurf über die Bemessung mit linear-elastischen ideal-plastischen Modellvorstellung abdecken. Die StrucEng Library soll in Zukunft im OpenSource Format zur Verfügung gestellt werden, womit die entsprechenden Modellvorstellungen von praxistätigen Ingenieuren/innen unter Verwendung einer benutzerfreundlichen Oberfläche frei verwendet werden können. Zudem werden in diversen Projekten die nichtlinearen Materialmodelle weiterentwickelt (z.B Korrosion, faserbewehrte Bauteile, etc.). In Zukunft werden zudem Lehrveranstaltungen und Weiterbildungsangebote im Bereich der numerischen Modellierung von Stahlbeton- und Mauerwerkstrukturen an der Professur für Massiv- und Brückenbau angeboten. Mit diesem besonderen Fokus in Lehre und Forschung auf die numerische Modellierung sind wir davon überzeugt, dass die angehenden Bauingenieure/innen fit für die zukünftigen Herausforderungen sind.
[1] Konrad Ernst Otto Zuse war ein deutscher Bauingieneur (!), Erfinder und Unternehmern. Mit seiner Entwicklung der Z3 im Jahre 1941 baute Zuse den ersten funktionsfähigken Computer der Welt.
[2] Im Rahmen diese Blogbeitragens wird immer von materiellen Nichtlinearität gesprochen. Des weiteren gibt es noch die geometrische Nichtlinearitäten (Berechnungen 2. Ordnung), welche über den P-Delta Effekt berücksichtigt werden.
Marius Weber
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to the English version: Long-term effects for designing piers monolithically connected to a prestressed girder or slab
In diesem Blogbeitrag geht es um ein technisch anspruchsvolles Thema: die Berücksichtigung von Langzeiteinflüssen (Schwinden und Kriechen) bei der Bemessung von Pfeilern, die monolithisch mit einem vorgespannten Träger oder einer Platte verbunden sind. Dieses strukturelle System findet man in monolithischen Bauwerken oder in Spannbetonbrücken. Wenn Sie sich für Tragwerksplanung begeistern und vielleicht sogar schon in Ihrer beruflichen Praxis damit zu tun hatten wird dieses Thema für Sie von grossem Interesse sein.
Der Entwurf von monolithischen, d.h. fugenlosen Bauwerken setzt sich beim Brückenbau in Europa immer mehr durch. Die Hauptgründe dafür sind zum einen der Wunsch, Probleme der Dauerhaftigkeit zu minimieren und die Instandhaltungskosten zu senken, und zum anderen, dass zunehmend Richtlinien für den Entwurf solcher Bauwerke zur Verfügung stehen. Die Schweiz ist ein Referenzland, das zur Entwicklung dieser Art von Bauwerken beigetragen hat. Traditionell werden Betonbrücken mit monolithisch mit der Fahrbahn verbundenen Pfeilern und halbintegrale oder integrale Brücken (monolithische Verbindung an beiden Widerlagern) [1], wo immer möglich, bevorzugt [2]. In der Schweiz wurden zahlreiche fugenlose Brücken [3][4][5][6][7] gebaut, und technische Richtlinien fördern integrale oder semi-integrale Brücken [1][2] (alte Referenz1Routes Nationales Suisses, Projects Standards de Ponts, Passage Supérieur avec Béquilles en V en Béton Coule sur Place, Departement Federak de L’Interieur, Bern 1972 aus den 70er Jahren). Angesichts der daraus resultierenden Tendenz, immer längere monolithische, fugenlose Brücken zu bauen, sind immer genauere und komplexere Berechnungen erforderlich, um die Pfeiler zuverlässig zu bemessen. Vor etwa zehn Jahren hatte ich die Gelegenheit, an einer Veröffentlichung mitzuwirken, die Ingenieure bei der Bemessung von Pfeilern langer fugenloser Betonbauwerke unterstützt [8]. Dieses Dokument ist allerdings auf Bauwerke beschränkt, bei denen die Platte oder der Träger nicht vorgespannt ist.
Trotz der Verfügbarkeit leistungsfähiger Statiksoftware bleibt die Analyse statisch unbestimmter Strukturen, die Langzeiteinflüssen ausgesetzt sind, eine Herausforderung. Ein anschauliches Beispiel dafür, das wir in diesem Blog erörtern werden, ist die Abschätzung der Biegemomente aufgrund von Langzeiteinflüssen in einem Betonpfeiler, der monolithisch mit einem vorgespannten Träger verbunden ist. Bei dieser Art von Bauwerk ist ein grosser Teil der Kräfte, die im Pfeiler wirken, auf die Verformungen zurückzuführen, die dem Pfeilerkopf durch das Deck aufgezwungen werden und die in den Grenzzuständen der Gebrauchstauglichkeit (GZG) und der Tragsicherheit (GZT Typ 2 und GZT Typ 42Obwohl die aufgezwungenen Verformungen (Schwinden und Kriechen) keine zyklischen Einwirkungen sind, sind sie im GZT Typ 4 (Ermüdungsversagen) für Betonermüdungsnachweise relevant, die von den absoluten maximalen und minimalen Betonspannungen abhängen.) relevant sind. Die Ermittlung der durch Langzeiteinflüsse verursachten Schnittgrössen im Pfeiler mit akzeptabler Genauigkeit ist jedoch kompliziert, da die Spannungen über der Zeit nichtlinear variieren (der Elastizitätsmodul variiert mit dem Alter des Betons), der Träger und der Pfeiler nicht gleichmässig kriechen (unterschiedliche Kriechkoeffizienten, d. h. unterschiedliche Betone und unterschiedliches Alter) und die gerissene Biegesteifigkeit über die Pfeilerhöhe variiert und von der Belastungsgeschichte abhängt (maximale Zugspannung). Um die Schnittgrössen in den Pfeilern einfach abschätzen zu können, berücksichtigen die Ingenieure in der üblichen Ingenieurpraxis daher in der Regel (i) reduzierte Pfeilerbiegesteifigkeiten aufgrund von Rissen (im Allgemeinen konstant oder linear variabel entlang der Pfeiler), die durch Iteration berechnet werden und für GZG-, GZT Typ 2- und GZT Typ 4-Nachweise unterschiedlich sind, (ii) etwa 40…50% des gesamten Schwindens der Fahrbahnplatte zur Zeit t = ∞, um die Langzeiteinflüsse zu berücksichtigen, aber (iii) vernachlässigen Langzeiteinflüsse aufgrund der Vorspannung mit der Begründung, dass das Kriechen des Pfeilers die Zunahme der Pfeilerkopfverschiebung aufgrund des Kriechens des Trägers kompensiert.
Die erste Vereinfachung kann im Allgemeinen akzeptiert werden, wenn sie mit dem nötigen technischen Sachverstand durchgeführt wird, sollte aber durch eine Sensitivitätsstudie ergänzt werden, um die Unsicherheiten der Berechnungen abzudecken. In Bezug auf die zweite und dritte Vereinfachung stellen sich jedoch unweigerlich folgende Fragen: Ist dieser Ansatz angemessen und unter welchen Bedingungen ist er gültig? Was ist der Hintergrund? Ist dieser Ansatz konservativ? Ist es notwendig, eine Sensitivitätsanalyse durchzuführen, um Unsicherheiten abzudecken, wenn diese Massnahme für den Entwurf entscheidend ist?
Nach dieser Einführung ist es nun an der Zeit, diese Fragen zu beantworten. Im Folgenden werden Sie und ich das formulierte Problem analytisch lösen, die Ergebnisse interpretieren und einige Schlussfolgerungen ziehen. Das zu untersuchende Bauwerk ist in Abbildung 1 vereinfacht dargestellt. Das horizontale Element stellt einen Spannbetonträger dar, das vertikale Element einen Pfeiler mit der Höhe h, der monolithisch mit dem Träger in einem Abstand LT (Ausdehnungslänge) vom Fixpunkt verbunden ist. Die mechanischen Eigenschaften sind für beide Elemente konstant und sind in Abbildung 1(a) dargestellt. Abbildung 1(b) und Abbildung 1(c) zeigen die horizontalen Verschiebungen des Pfeilerkopfes über die Zeit, uh,εcs(t) und uh,P,el(t), verursacht durch das Schwinden ecs(t) bzw. die Vorspannung P(t) des Trägers. Beachten Sie, dass die Einspannung des Pfeilers in die horizontalen Verschiebungen des Trägers vernachlässigt wird, da die axiale Steifigkeit des Trägers im Allgemeinen um Grössenordnungen höher ist als die horizontale (Biege-)Steifigkeit des Pfeilers. Darüber hinaus wurden für die in Abbildung 1(c) dargestellten Gleichungen folgende Annahmen getroffen: Normalkraft konstant entlang des Trägers (keine Vorspannungkraftverluste durch Reibung) und EPIP<<EGIG, d.h. Pfeiler “perfekt” doppelt eingespannt. Es ist zu beachten, dass die letztgenannte Überlegung für einige Fälle nicht geeignet ist, z. B. für Bauwerke, bei denen die Biegesteifigkeit der Stütze im Vergleich zu der des Trägers nicht vernachlässigbar ist, oder für flexible Fundamente (Tiefgründungen). Die im Folgenden berechneten Langzeiteinflüsse werden jedoch unabhängig von den Steifigkeiten der Pfeiler und der Fahrbahnplatte formuliert, die direkt als aufgezwungene Verformungen in die Finite-Elemente-Analyse (FEA) einbezogen werden können. Darüber hinaus wird der Einfluss des Kriechens des Pfeilers auf die entsprechenden (ungerissenen und gerissenen) Biegesteifigkeiten in den folgenden Berechnungen nicht berücksichtigt, so dass die äquivalente reduzierte Biegesteifigkeit des Pfeilers unter Berücksichtigung von Kriechen und Rissbildung im statischen System verwendet werden sollte.
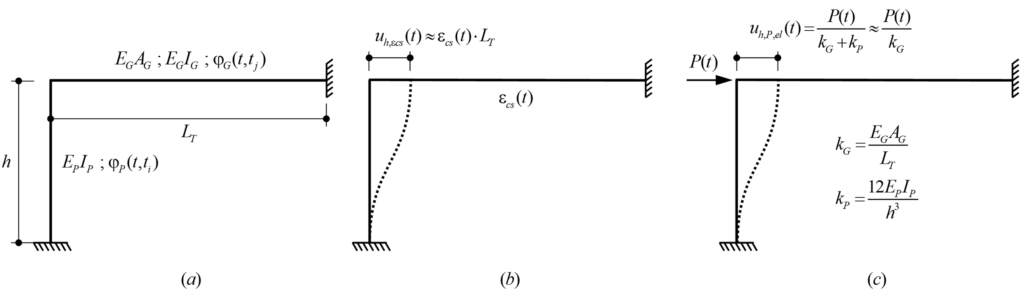
EG: Elastizitätsmodul des Trägers
EP: Elastizitätsmodul des Pfeilers
IG: Flächenträgheitsmoment des Trägers
IP: Flächenträgheitsmoment des Pfeilers
φG(t,tj): Kriechkoeffizient des Trägers
φP(t,ti): Kriechkoeffizient des Pfeilers
Um das System analytisch zu lösen, wird die Rahmenstruktur aus Abbildung 1 gemäss Abbildung 2 vereinfacht. Um die Schnittgrössen im Pfeiler infolge der aufgezwungenen horizontalen Verschiebung uh, zu erhalten, kann der isolierte doppelt-eingespannte Pfeiler der Höhe h (Abbildung 2 (a)) durch den isolierten gelenkig eingespannten Pfeiler der Höhe h/2 (Abbildung 2 (b)) ersetzt werden. Abbildung 2(c) zeigt somit das äquivalente vereinfachte System zur Ermittlung der Schnittgrössen im Pfeiler infolge einer horizontalen Verschiebung u’h am Pfeilerkopf, die gleich der Hälfte der horizontalen Verschiebung uh im ursprünglichen System (Abbildung 1) ist, d. h. u’h (t)= uh(t)/2. Um die korrekte Verschiebung des Pfeilerkopfes infolge der Vorspannung zu erhalten, ist die äquivalente Vorspannkraft P’ (t) im vereinfachten System (Abbildung 2(c)) gleich der Hälfte der Vorspannkraft P(t)/2 im ursprünglichen System (Abbildung 1), wenn die Biegesteifigkeit des Pfeilers gegenüber der axialen Steifigkeit des Trägers vernachlässigt wird, andernfalls wird sie wie folgt bestimmt:
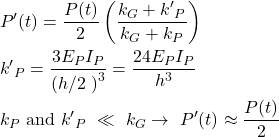
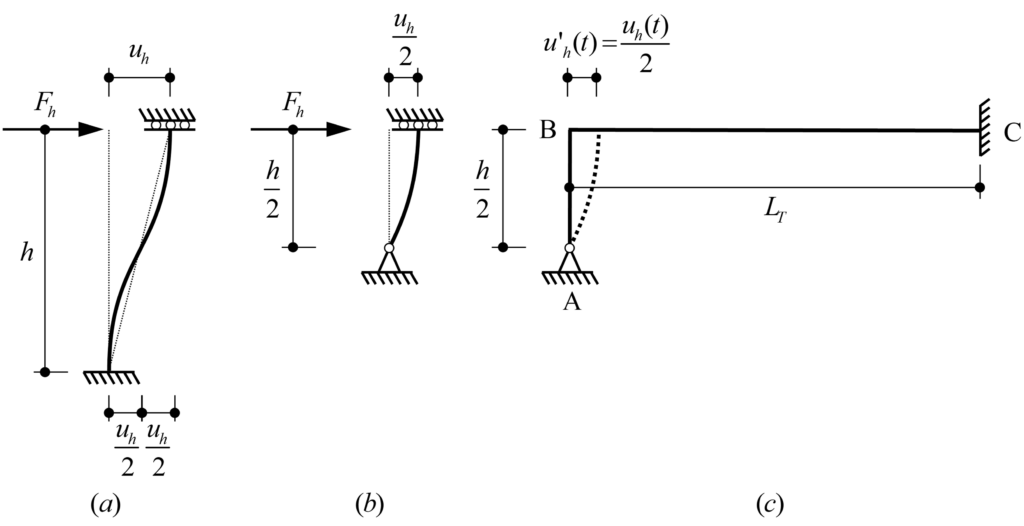
Im Folgenden isolieren wir den Pfeiler des in Abbildung 2(c) dargestellten vereinfachten Systems und lösen ein System, das aus einem Pfeiler mit einem einzigen Grad statischer Unbestimmtheit besteht, indem wir die zeitabhängige Kraftmethode anwenden und die Kompatibilitätsgleichungen über die Zeit formulieren, wobei:
BS (Basissystem): Feste Rotation in B (Pfeilerkopf) freigegeben
ÜG (Überzählige Grösse): Biegemoment in B (Pfeilerkopf)
Zusätzlich werden die zeitabhängigen Biegemomente am Pfeilerkopf infolge Schwinden und Vorspannung separat berechnet.
Zeitabhängiges Verhalten von Betonpfeilern
1. Schwinden (zeitabhängige Pfeilerkopfverschiebung3Beachten Sie, dass die Pfeilerkopfverschiebungen analog zu den Setzungen in unserer Vorlesung über Langzeiteinflüsse behandelt werden können (zeitunabhängig oder zeitabhängig).)
Abbildung 3 zeigt den isolierten Pfeiler mit dem Basissystem (BS) und der überzähligen Grösse (ÜG), die zur Bestimmung des Biegemoments MB(t) mit Hilfe der Kraftmethode verwendet wird. Da sich das Biegemoment MB(t) über die Zeit verändert, wird die Kompatibilität am Auflager B sowohl zum Anfangszeitpunkt als auch zeitabhängig ausgedrückt.
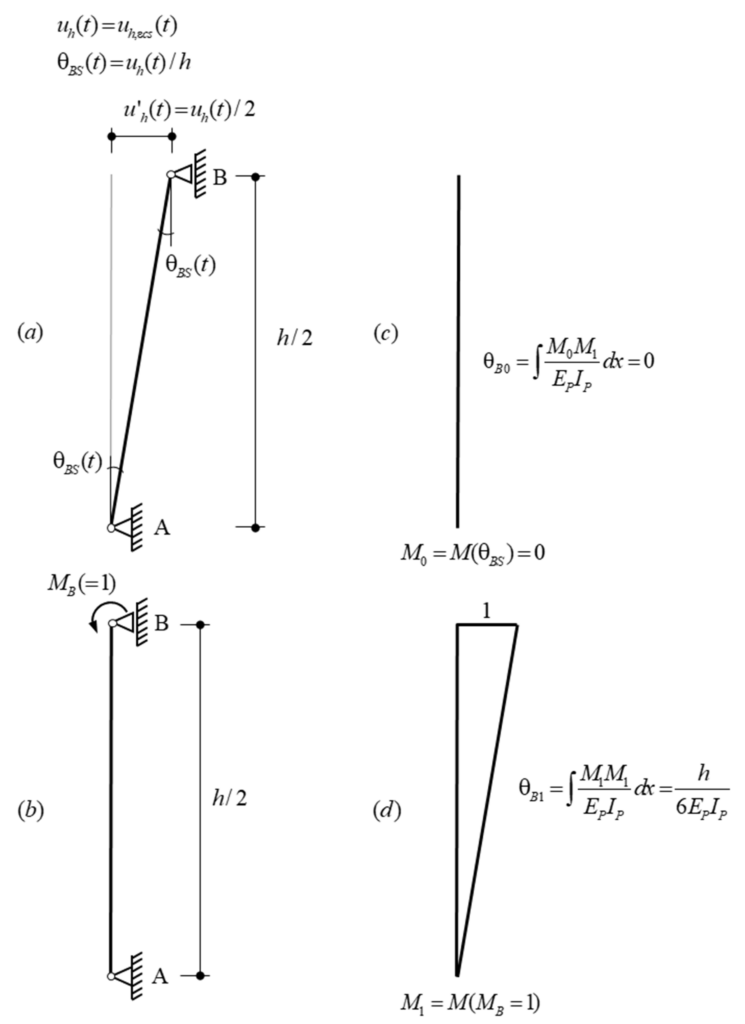
Das Schwinden εcs(t) des Trägers verursacht eine Verformung über die Zeit, die horizontale Verschiebungen uh(t) und Biegemomente MB(t) am Pfeilerkopf erzeugt. Zum Anfangszeitpunkt sind sowohl die horizontale Verschiebung uh(t0) als auch das Biegemoment MB(t0) Null (kein Schwinden). Zu jedem beliebigen Zeitpunkt t > t0, ist der Träger um εcs(t) geschwunden, was zu einer horizontalen Verschiebung uh(t) und einem Biegemoment MB(t) führt, siehe Abbildung 4(a) bzw. Abbildung 4(b). Unter der Annahme, dass das Schwinden des Trägers und damit die aufgezwungenen Verformungen über die Zeit uh(t) proportional zur Kriechfunktion des Pfeilers sind, kann uh(t) wie folgt ausgedrückt werden:
![]()
Daher erreicht die horizontale Verschiebung am Pfeilerkopf zur Zeit t = ∞ die maximale horizontale Verschiebung uh,∞ = εcs,∞·LT (Abbildung 4(a)). Wie wir jedoch weiter unten sehen werden, wird das Biegemoment MB,∞ (t=∞) geringer sein als das elastische Biegemoment MB,el,∞ das durch die maximale horizontale Verschiebung uh,∞ verursacht wird (Abbildung 4(b)).
Das Biegemoment MB(t) am Pfeilerkopf kann wie folgt formuliert werden:
![]()
Dabei ist ΔMB(t) die Zunahme des Biegemoments über die Zeit infolge des Schwindens.
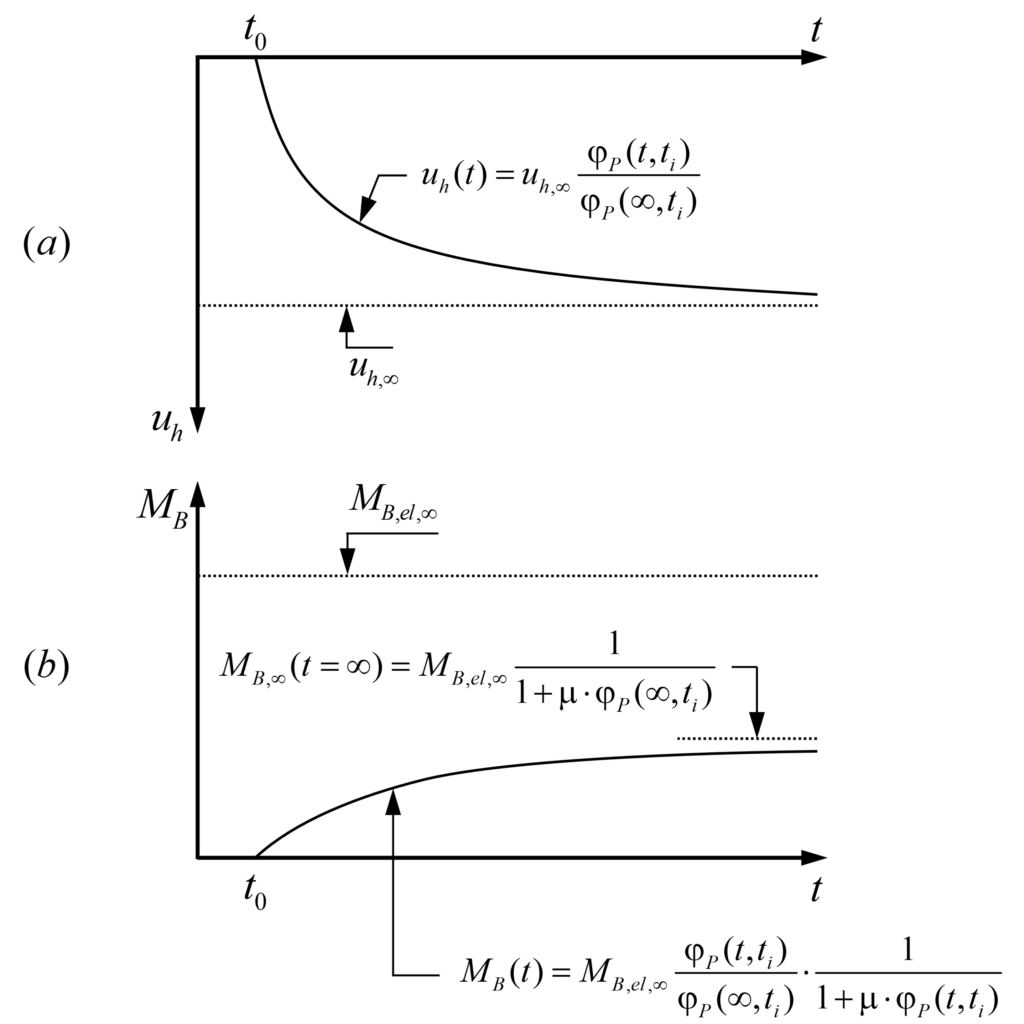
Rotationskompatibilitätsbedingung zum Anfangszeitpunkt t=t0:
Die Rotationskompatibilität zum Anfangszeitpunkt (man beachte, dass alle Operationen im Basissystem (BS) angewendet werden) ergibt den Ausdruck:
![]()
Wie bereits erwähnt, ist das Biegemoment am Pfeilerkopf zum Anfangszeitpunkt gleich Null MB(t0) = 0, da das Schwinden noch nicht eingesetzt hat.
Zeitabhängige Rotationskompatibilitätsbedingung (Methode von Trost):
Die Entwicklung der zeitabhängigen Rotationskompatibilität erfolgt nach der Methode von Trost. Wenn Sie mit dieser Methode nicht vertraut sind, empfehle ich Ihnen unsere Vorlesung zu Langzeiteinflüssen in Advanced Structural Concrete.
![Rendered by QuickLaTeX.com \begin{align*}& {{\theta }_{B}}(t)=\cancel{{{\theta }_{B0}}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+\cancel{{{M}_{B}}({{t}_{0}})}\cdot {{\theta }_{B1}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+\Delta {{M}_{B}}(t)\cdot {{\theta }_{B1}}\left[ 1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]={{\theta }_{BS}}(t)\text{ (Gl. 4)} \\& {{\theta }_{BS}}(t)={{\theta }_{BS,\infty }}\frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})} \\& \Delta {{M}_{B}}(t)={{M}_{B}}(t)=\frac{{{\theta }_{BS,\infty }}}{{{\theta }_{B1}}}\cdot \frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})}\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})} \\& {{M}_{B,el,\infty }}=\frac{{{\theta }_{BS,\infty }}}{{{\theta }_{B1}}}=\frac{6{{E}_{P}}{{I}_{P}}}{{{h}^{2}}}{{\varepsilon }_{cs,\infty }}{{L}_{T}}\text{ (Gl}\text{. 5)} \\& {{M}_{B}}(t)={{M}_{B,el,\infty }}\cdot \frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})}\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 6)} \\& {{M}_{B,\infty }}(t=\infty )={{M}_{B,el,\infty }}\frac{1}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})}\text{ (Gl}\text{. 7)} \\\end{align*}](https://concrete.ethz.ch/wp-content/ql-cache/quicklatex.com-70d44fed1655e011294966bb18605b31_l3.png)
Beachten Sie, dass die Kompatibilitätsgleichung (Gl. 4) ausdrückt, dass die durch das Biegemoment MB(t) verursachte Rotation θB(t) (überzählige Grösse ÜG) die Rotation aufgrund der Pfeilerkopfverschiebung θBS(t) kompensieren muss; beide Rotationen werden im Basissystem bestimmt. Mit anderen Worten, die Gesamtrotation des Pfeilerkopfes B muss gleich Null sein (siehe Abbildung 3). Der von Trost eingeführte Alterungskoeffizient μ4Der Alterungsbeiwert μ könnte durch Lösen einer linearen und inhomogenen Volterra-Integralgleichung ermittelt werden, aber für typische Fälle kann man μ ≈ 0.8 annehmen. trägt der Tatsache Rechnung, dass der Beton bei später einwirkenden Lasten weniger kriecht. Aus dieser Bedingung lässt sich das Biegemoment MB(t) zu jedem Zeitpunkt t bestimmen (Gl. 6) und in Form des elastischen Biegemoments MB,el,∞ (Gl. 5) ausdrücken.
2. Vorspannung
Im Gegensatz zum Schwinden, bei dem die horizontale Verschiebung am Pfeilerkopf von Null zum Anfangszeitpunkt zunimmt, ist die Vorspannung eine sofortige Einwirkung zum Anfangszeitpunkt (t=t0), die eine anfängliche horizontale Verschiebung uh(t0) = uh,P,el(t0) und ein entsprechendes anfängliches elastisches Biegemoment MB(t0) = MB,el(t0) am Pfeilerkopf verursacht. Danach ändern sich sowohl die horizontale Verschiebung uh(t) als auch das Biegemoment MB(t) über die Zeit.
Ähnlich wie bei der Berechnung der Biegemomente infolge Schwinden wird der Pfeiler isoliert und das Basissystem (BS) mit dem Biegemoment am Pfeilerkopf B MB(t) als überzählige Grösse verwendet, siehe Abbildung 5.
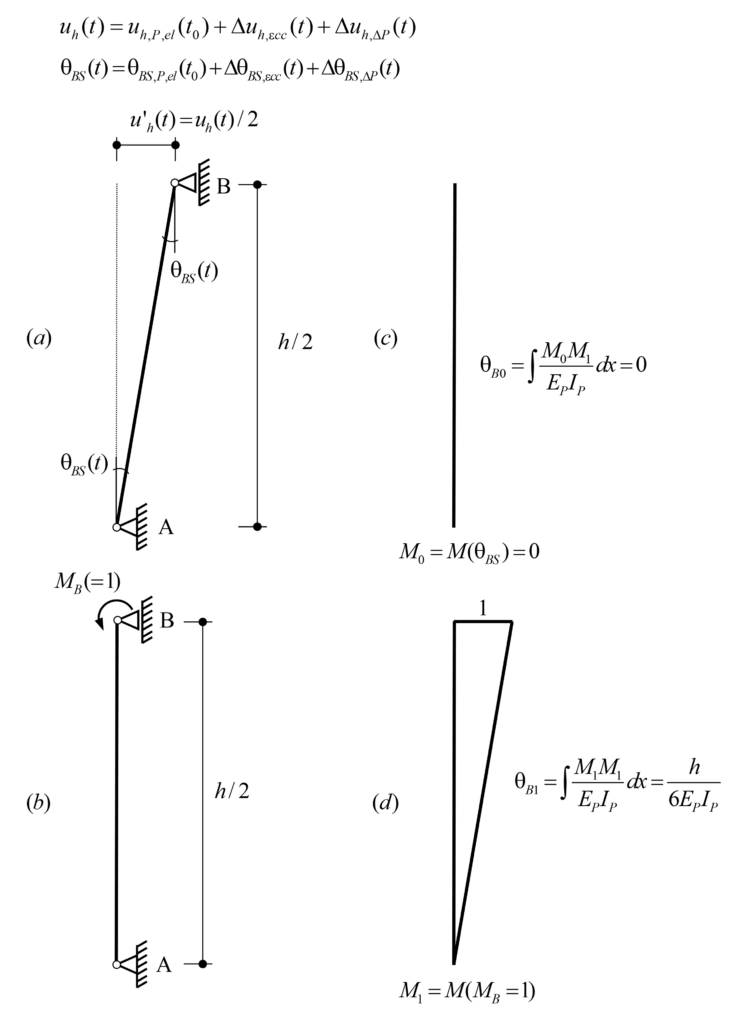
Die gesamte horizontale Verschiebung am Pfeilerkopf uh(t) infolge der Vorspannung beträgt:
![]()
wobei,
uh,P,el(t0) die anfängliche horizontale Verschiebung am Pfeilerkopf infolge der elastischen Verformung des Trägers durch die anfängliche Vorspannkraft P(t0) ist, d.h.,
![]()
Δuh,ecc(t) ist der horizontale Verschiebungszuwachs am Pfeilerkopf über die Zeit aufgrund von Langzeiteffekten, die durch das Kriechen des Trägers φG(t,tj) verursacht werden.
![]()
Δuh,DP(t) ist der horizontale Verschiebungszuwachs am Pfeilerkopf über die Zeit infolge der Änderung der Vorspannkraft ΔP(t) (Vorspannkraftverluste) über die Zeit aufgrund von Schwinden, Kriechen und Relaxation. Sie wird als proportional zur anfänglichen horizontalen Verschiebung uh,P,el(t0) betrachtet und hat einen negativen Wert, da ΔP(t) <0:
![]()
Wenn die Vorspannkraft zum Anfangszeitpunkt (t=t0) aufgebracht wird, weist der Pfeilerkopf eine anfängliche horizontale elastische Verschiebung uh,P,el(t0) auf. Anschliessend nimmt die horizontale Verschiebung aufgrund des Kriechens des Trägers Δuh,εcc(t) mit der Zeit zu, was teilweise durch die Abnahme der Vorspannkraft aufgrund der Vorspannkraftverluste Δuh,ΔP(t) kompensiert wird, siehe Abbildung 6(a). Andererseits wird das Biegemoment MB,el(t0) im Pfeilerkopf, das durch die aufgezwungene horizontale Verschiebung uh,P,el(t0), die elastische Verformung des Trägers infolge der Vorspannung, verursacht wird, im Laufe der Zeit aufgrund des Kriechens und der Vorspannkraftverluste ΔP(t) des Pfeilers verringert (Abbildung 6(b)). Das Biegemoment MB(t) kann wie folgt ausgedrückt werden:
![]()
Dabei ist ΔMB(t) die Zunahme des Biegemoments über die Zeit aufgrund des Kriechens des Pfeilers und des Trägers sowie der Vorspannkraftverluste.
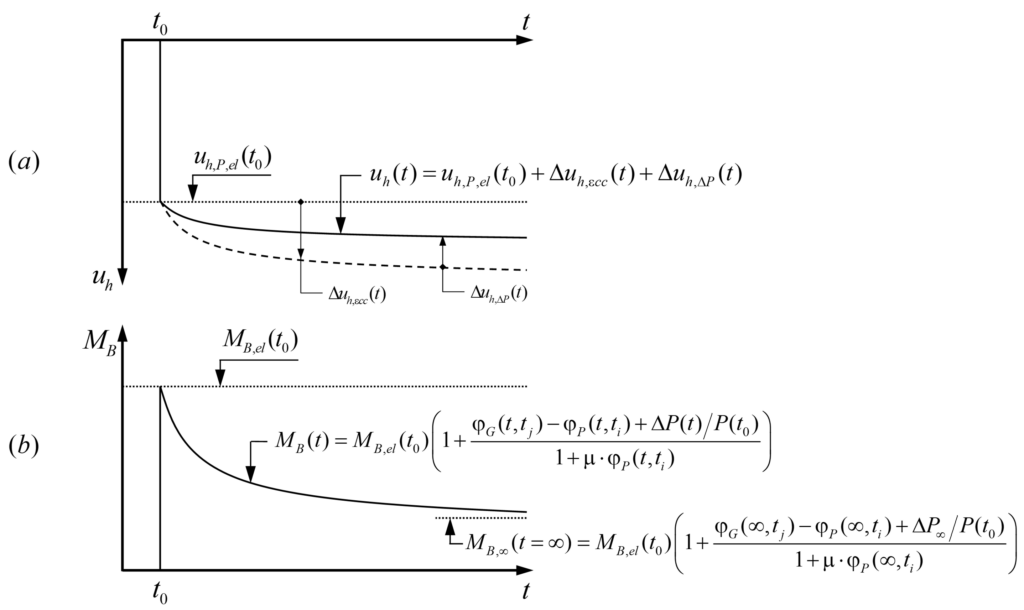
Für die Berechnung der Biegemomente MB(t) am Pfeilerkopf über die Zeit wird, ähnlich wie bei der Berechnung des Schwindens, erstens die Rotationskompatibilität zum Anfangszeitpunkt und zweitens die zeitabhängige Rotationskompatibilität nach der Methode von Trost angewendet.
Rotationskompatibilitätsbedingung zum Anfangszeitpunkt t=t0:
Die Rotationskompatibilität im Basissystem (BS) zum Anfangszeitpunkt (Abbildung 5) ergibt:
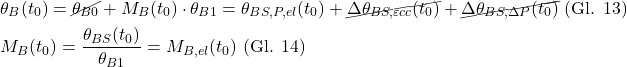
Das anfängliche Biegemoment MB(t0) am Pfeilerkopf ist gleich dem anfänglichen elastischen Biegemoment MB,el(t0), siehe Gl. 14.
Zeitabhängige Rotationskompatibilitätsbedingung (Methode von Trost):
Im Folgenden werden die Gleichungen mit Hilfe der Methode von Trost entwickelt, um den Biegemomentzuwachs am Pfeilerkopf über die Zeit ΔMB(t) zu bestimmen.
![]()
Beachten Sie, dass die Rotation am Auflager B θB(t) über die Zeit, analog zur horizontalen Verschiebung, ergibt:
![]()
wobei,
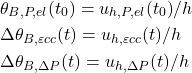
Durch Substitution von Gl. 13 und Gl. 14 in Gl. 15:
![Rendered by QuickLaTeX.com \begin{align*} & {{\theta }_{B}}(t)={{M}_{B,el}}({{t}_{0}})\cdot {{\theta }_{B1}}\cdot {{\varphi }_{P}}(t,{{t}_{i}})+\Delta {{M}_{B}}(t)\cdot {{\theta }_{B1}}\left[ 1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]=\Delta {{\theta }_{BS,\varepsilon cc}}(t)+\Delta {{\theta }_{BS,\Delta P}}(t)\text{ (Gl}\text{. 16)} \\ & \Delta {{M}_{B}}(t)=\left[ \frac{\Delta {{\theta }_{BS,\varepsilon cc}}(t)}{{{\theta }_{B1}}}+\frac{\Delta {{\theta }_{BS,\Delta P}}(t)}{{{\theta }_{B1}}}-{{M}_{B,el}}({{t}_{0}})\cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 17)} \\\end{align*}](https://concrete.ethz.ch/wp-content/ql-cache/quicklatex.com-349d2964b989872ee68f2ae98ce85bfa_l3.png)
Andererseits kann angenommen werden, dass das Biegemoment und die Rotation am Pfeilerkopf proportional zur horizontalen Verschiebung über die Zeit sind. Daher kann man aus Gl. 10 und Gl. 11 die Biegemomenterhöhungen ΔMB,εcc,el(t) und ΔMB,ΔP,el(t) aufgrund von Kriech- bzw. Vorspannkraftverlusten wie folgt formulieren:
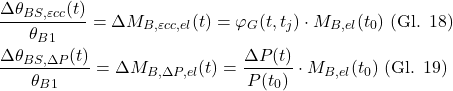
Durch Substitution von Gl. 18 und Gl. 19 in Gl. 17:
![Rendered by QuickLaTeX.com \[\Delta {{M}_{B}}(t)={{M}_{B,el}}({{t}_{0}})\cdot \frac{{{\varphi }_{G}}(t,{{t}_{j}})-{{\varphi }_{P}}(t,{{t}_{i}})+\frac{\Delta P(t)}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 20)}\]](https://concrete.ethz.ch/wp-content/ql-cache/quicklatex.com-cdb79ed3c53318a9454a3d018115edf4_l3.png)
Durch Einsetzen des Biegemomentinkrements ΔMB(t) aus Gl. 20 in Gl. 12 ergibt sich schliesslich das Gesamtbiegemoment am Pfeilerkopf über die Zeit MB(t) wie folgt:
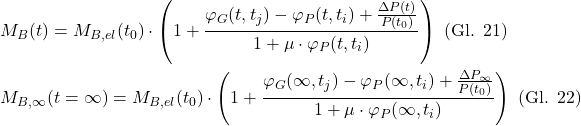
3. Zusammenfassung und Diskussion
Schwinden:
Das Biegemoment MB,∞ am Pfeilerkopf zur Zeit t = ∞ infolge des Schwindens ist wie folgt:
![]()
Dabei ist μ ≈ 0.80 und ti das Alter des Pfeilerbetons, wenn der Träger zu schwinden beginnt. Abbildung 7 zeigt das Verhältnis zwischen dem Biegemoment MB,∞ und dem elastischen Biegemoment MB,el,∞ am Pfeilerkopf zur Zeit t = ∞ als Funktion des Pfeiler-Kriechkoeffizienten φP(∞,ti).
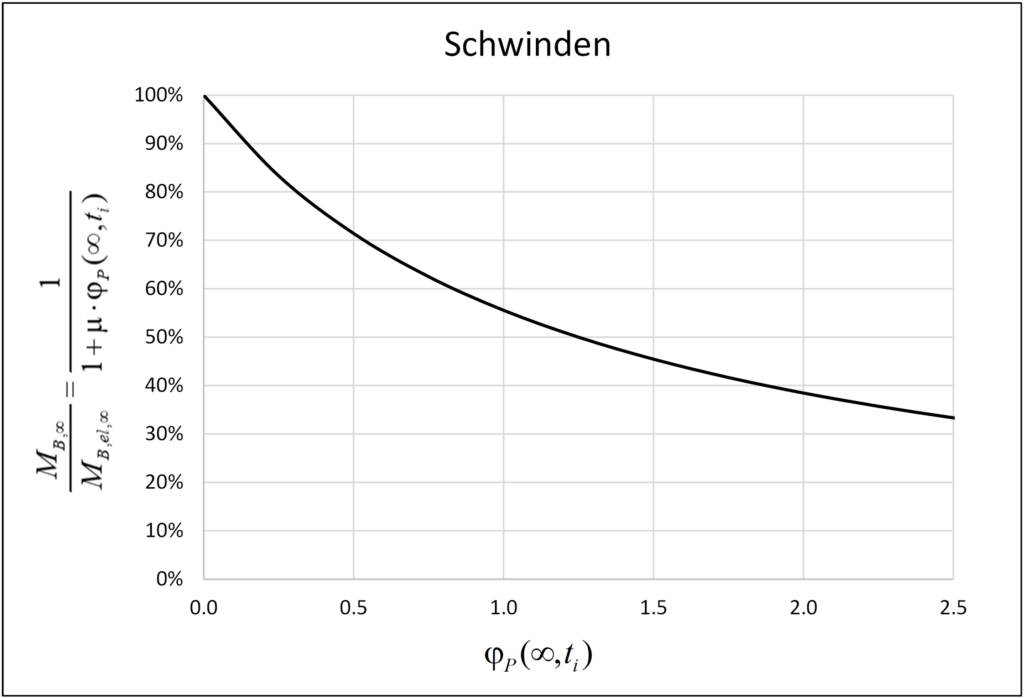
Das Biegemoment MB(t) am Pfeilerkopf infolge Schwinden wächst mit der Zeit an, bis es zur Zeit t = ∞ ein maximales Biegemoment MB,∞ erreicht (siehe Abbildung 4(b)), das das 1/(1+μ·φP(∞,ti)) fache des elastischen Biegemoments MB,el,∞ infolge der kurzfristigen Wirkung des Gesamtschwindens εcs,∞ beträgt.
Das maximale Biegemoment MB,∞ am Pfeilerkopf zur Zeit t = ∞, das unabhängig vom Kriechkoeffizienten φG(∞,ti) des Trägers ist, ist gleich 38%·MB,el,∞ für einen typischen Wert von φP(∞,ti) = 2.0. Aus diesem Grund berücksichtigen viele Ingenieure 40% des Gesamtschwindens (40%·φcs,∞), um die Schnittgrössen in den Pfeilern zur Zeit t = ∞ aufgrund von Langzeiteinflüssen zu bestimmen. Da die Pfeiler jedoch vor dem Träger gebaut werden, ist der Pfeilerkriechkoeffizient im Betonalter, in dem der Träger zu schwinden beginnt, oft kleiner als 2.0 und in Regionen mit hoher relativer Luftfeuchtigkeit ohnehin kleiner (z. B. φP(∞,t0) ≈ 1.8 für C30/37 und RH ≈ 80%, wie in der Schweiz üblich). Wird darüber hinaus die vorteilhafte Wirkung eines gerissenen Pfeilers mit entsprechend reduzierter Steifigkeit berücksichtigt, muss ein noch geringerer äquivalenter Kriechkoeffizient φP (ermittelt z.B. aus einer Querschnittsanalyse als Verhältnis der Krümmungen mit und ohne Kriechen) verwendet werden. Wenn die Ingenieure nicht über diesen Hintergrund verfügen und wahllos den Referenzwert von 40% (φP(∞,ti) = 2.0) oder sogar einen reduzierten Wert für das Schwinden aufgrund der hohen Luftfeuchtigkeit verwenden, kann der Entwurf der Pfeiler auf der unsicheren Seite liegen, insbesondere bei GZG. Betrachtet man beispielsweise einen Pfeiler-Kriechkoeffizienten zur Zeit t = ∞ von φP(∞,ti) = 1.25 ab dem Zeitpunkt, an dem der Träger zu schwinden beginnt, so beträgt das Biegemoment am Pfeilerkopf MB,∞ = 50%·MB,el,∞, d.h. 32% höher als MB,∞ = 38%·MB,el,∞ für φP(∞,ti) = 2.0.
Vorspannung:
Das Biegemoment MB,∞ am Pfeilerkopf zur Zeit t = ∞ infolge der Vorspannung (einschliesslich kurz- und langfristigen Einflüssen) beträgt:
![Rendered by QuickLaTeX.com \[{{M}_{B,\infty }}={{M}_{B,el}}({{t}_{0}})\cdot \left( 1+\frac{{{\varphi }_{G}}(\infty ,{{t}_{j}})-{{\varphi }_{P}}(\infty ,{{t}_{i}})+\frac{\Delta {{P}_{\infty }}}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})} \right)\]](https://concrete.ethz.ch/wp-content/ql-cache/quicklatex.com-17534854d9d020a94b6d2381226cbdb9_l3.png)
wobei tj und ti das Betonalter des Trägers bzw. des Pfeilers bei Einwirkung der Vorspannung sind.
Abbildung 8 zeigt das Verhältnis zwischen dem Biegemomentzuwachs ΔMB,∞ und dem anfänglichen elastischen Biegemoment MB,el(t0) am Pfeilerkopf zur Zeit t = ∞. Wie bei der Bemessung häufig angenommen, wirkt das Kriechen des Pfeilers zusammen mit dem (negativen) Beitrag der Vorspannungsverluste dem Anstieg der Biegemomente am Pfeilerkopf, der durch das Kriechen des Trägers verursacht wird, entgegen und kompensiert ihn bei bestimmten Werten der Kriechkoeffizienten sogar. In typischen Fällen sind jedoch erhebliche Unterschiede zu beobachten. Im Allgemeinen ist das Verhältnis ΔMB,∞ / MB,el(t0) eine Funktion des Pfeiler-Kriechbeiwerts φP(∞,ti), des Träger-Kriechbeiwerts φG(∞,tj), der Vorspannkraftverluste ΔP∞/P(t0) und des Alterungsbeiwerts μ. Die in Abbildung 8 dargestellten Kurven wurden für μ=0.80, φG(∞,tj) = {1.0; 1.5; 2.0} und ΔP∞/P(t0)= {0%; 10%} erstellt. Man kann feststellen, dass die Vorspannkraftverluste eine geringe Auswirkung auf das Verhältnis ΔMB,∞ / MB,el(t0) haben (etwa 5 % für die verwendeten Parameter), was in den Berechnungen vernachlässigt werden kann.
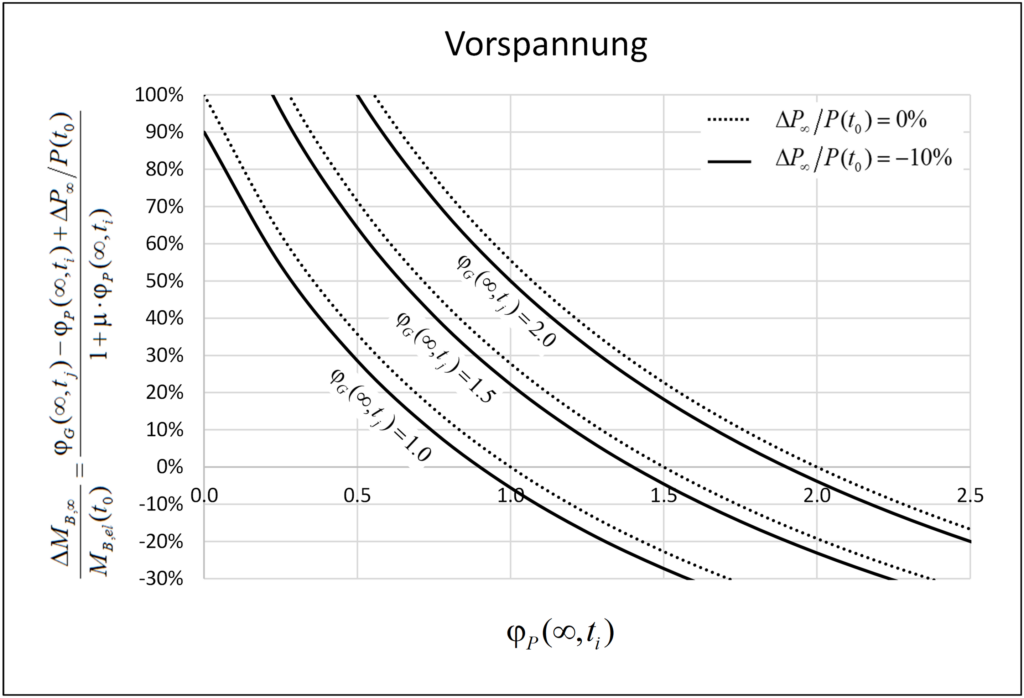
Das Verhältnis ΔMB,∞ / MB,el(t0) hängt von den Kriechkoeffizienten des Trägers und des Pfeilers (mit ti und tj = Betonalter dieser Elemente zum Zeitpunkt des Aufbringens der Vorspannung) sowie von den Vorspannungsverlusten ab. Das anfängliche Biegemoment MB,el(t0) am Pfeilerkopf nimmt im Laufe der Zeit ab, wenn der Kriechkoeffizient des Pfeilers φP(∞,ti) höher ist als der Kriechkoeffizient des Trägers φG(∞,tj), d. h. φP(∞,ti) > φG(∞,tj), und nimmt andernfalls zu (unter Vernachlässigung der Vorspannungsverluste), was typischerweise zutrifft, da die Pfeiler vor den Trägern gebaut werden.
Bei einem Pfeiler-Kriechkoeffizienten von φP(∞,ti) = 1.25 erhöht sich das Biegemomentinkrement ΔMB,∞ zur Zeit t = ∞ um etwa 10 % bzw. 35 % gegenüber dem anfänglichen Biegemoment MB,el(t0) für Träger-Kriechkoeffizienten von φG(∞,tj) = 1.5 bzw. φG(∞,tj) = 2.0. Ein Anstieg von 35 % ist nicht von vornherein vernachlässigbar; er kann jedoch für niedrige und mittlere Vorspannungsniveaus des Trägers vernachlässigt werden, da der Biegemomentenzuwachs ΔMB,∞ im Vergleich zu dem durch Schwinden verursachten Biegemoment in der Regel gering ist.
4. Schlussfolgerungen
Für eine vorläufige Bemessung (Abschätzung der inneren Einwirkung) von Pfeilern, die monolithisch mit einem vorgespannten Träger verbunden sind, ist es eine gültige Näherung, 40…50 % des Gesamtschwindens zur Zeit t = ∞ εcs,∞ zu berücksichtigen und die über die Zeit zunehmende innere Kraft infolge der Vorspannung zu vernachlässigen. Diese Überlegungen können auch bei der Detailplanung akzeptabel sein, wenn die Bemessung der Pfeiler nicht entscheidend ist und der Planer den Einfluss der Langzeiteinflüsse auf das Bauwerk, einschliesslich des Bauprozesses, kontrollieren kann. Im Allgemeinen kann jedoch die Verwendung eines Wertes von 40%·εcs,∞ zur Berücksichtigung der langfristigen Auswirkungen unsicher sein, da die in den Pfeilern wirkenden Schnittgrössen unterschätzt werden.
Die vorgestellten Gleichungen zur Abschätzung der Schnittgrössen in den Pfeilern aufgrund der Langzeiteinflüsse sind in der Ingenieurpraxis nützlich. Sie ermöglichen eine einfache, aber wesentlich genauere Langzeitanalyse, wie sie für lange fugenlose Bauwerke mit monolithischen Pfeiler-Träger-Verbindungen erforderlich ist. Darüber hinaus kann eine geeignete Strategie der Betonierabschnitte dazu beitragen, die Länge von fugenlosen Bauwerken deutlich zu erhöhen.
Abschliessend wird darauf hingewiesen, dass die durch Schwinden und Vorspannung verursachten Momente an den Pfeilerköpfen aufgrund des Kriechens der Pfeiler zwar reduziert werden, dass aber bei der Bemessung von Lagern und Dehnungsfugen und der Abschätzung von Brückenendverschiebungen in integralen Widerlagern die vollen Trägerverschiebungen berücksichtigt werden müssen.
Ich hoffe, dass dieser Beitrag für Sie von Interesse und Nutzen war. Wir freuen uns über Kommentare und Anregungen.
Alejandro Giraldo Soto
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to the English version: Ductility and rotation capacity of structural concrete
Was ist Duktilität? Warum brauchen wir sie?
Die Duktilität ist ein allgegenwärtiges Konzept im Bauingenieurwesen und im Stahlbetonbau, dem Feld um das sich dieser Blogpost handelt.
Im Erdbebeningieurwesen haben bekannte Autoren folgende Definition der Duktilität vorgeschlagen.
Der Begriff Duktilität bezeichnet die Fähigkeit eines Tragelementes oder Tragwerks, sich nicht nur elastisch, sondern unter Aufrechterhaltung des Tragwiderstandes auch plastisch zu verformen.
(Paulay, Bachmann, Moser ,1990: Erdbebenbemessung von Stahlbetonhochbauten)
The term “ductility” in structural design is used to mean the ability of a structure to undergo large deformations in the postelastic range without a substantial reduction in strength.
(Park, 1991: Ductility of Structural Concrete)
Die Definitionen stammen aus dem Erdbebeningenieurwesen und zielen darauf ab übermässige Schäden bei grossen plastischen Verformungen zu vermeiden. Daher werden manchmal geringe Lastabfälle, oder Entfestigung akzeptiert. Dies ist im Bauingenieurwesen unüblich und unkonservativ, da die meisten Einwirkungen lastgesteuert sind und Versagen bei Höchstlast eintritt.
Paulay, Bachmann und Moser (1990) schlagen vor, je nach Massstab verschiedene Arten der Duktilität zu betrachten, nämlich Dehnungsduktilität auf Materialebene, Krümmungsduktilität auf Querschnittsebene, Rotationsduktilität für plastische Gelenke und die Verschiebeduktilität bei statischen Systemen. Die Duktilität wird jeweils als Verhältnis der betrachteten Grösse (z.B. Dehnung, Krümmung) bei Versagen und bei Fliessbeginn berechnet.
Im Bauingenieurwesen ist die Duktilität in der SIA 260 (2013) wie folgt definiert:
Durch irreversible Verformungen und Energiedissipation charakterisiertes, in der Regel auf die Grenze des elastischen Verhaltens bezogenes plastisches Verformungsvermögen.
Im Bauingenieurwesen ist Duktilität notwendig um die Plastizitätstheorie anzuwenden, um Lastumlagerungen zu ermöglichen und um Eigenspannungszustände vernachlässigen zu können. Dieses Konzept findet sich auch in Normen, wie den SIA Normen oder den Eurocodes wieder. Laut SIA 262 (2013) darf die Plastizitätstheorie nur angewendet werden, wenn duktiles Verhalten sichergestellt werden kann. Lastumlagerungen sind bei kleinem Verhältnis x/d, duktilem Bewehrungsstahl und normalfestem Beton erlaubt. Die Eurocodes erlauben das Vernachlässigen von Eigenspannungszustände, wie Temperatureffekten, differentiellen Setzungen und Schwinden, falls das Verformungsvermögen und das Rotationsvermögen genügend sind (n.b. in der englischen Version des Eurocode 2 ist Verformungsvermögen zu «ductility» übersetzt). Es gibt keine Angabe zur Bestimmung des Verformungsvermögens, aber ein Nachweis des Rotationsvermögens ist in der Norm enthalten (siehe zweiter Abschnitt).
Während die exakte Definition der Duktilität nicht eindeutig ist, sind die meisten Autor:innen sich einig warum duktil gebaut werden sollte. Die Argumente können grob zu zwei Hauptideen zusammengefasst werden:
- Verhindern von unvorhergesehenem Versagen (Versagensankündigung, Robustheit erreichen, Sicherheit bei Erdbeben oder anderen aussergewöhnlichen Einwirkungen)
- Umlagerung von Schnittkräften (Biegemomentenverteilungen die nicht der elastischen entsprechen, Vernachlässigung von Eigenspannungszuständen)
Ein bekanntes Beispiel, wo Duktilität das Versagen verhindert hat, ist die Reussbrücke Wassen, die grosse Setzungen nach dem Unwetter von 1987 überlebt hat und repariert werden konnte (Abbildung 1).

Ist Stahlbeton duktil? Wie stellt man das bei der Bemessung sicher?
Wie gerade gesehen kann Stahlbeton duktil sein. Es stellt sich die Frage, wie bei der Bemessung bestimmt werden kann ob ein Bauwerk ausreichend duktil sein wird. Hier werden zwei Vorgehensweisen vorgestellt.
In der Schweizer Baupraxis wird Duktilität durch bestehendes Wissen über günstige Konstruktionsmassnahmen erreicht. Beispiele für solche Massnahmen sind die Wahl von angemessenen, bewährten Materialien, Mindestbewehrungen und Verbügelung um spröde Schub- oder Druckzonenversagen zu vermeiden. Die Massnahmen stützen auf Erfahrung und experimentell validierten Forschungsergebnissen ab, was gleichzeitig ihr grösster Nachteil ist. Während sie in Standardfällen sehr effizient sind, erschweren sie zum Beispiel die Verwendung von neuen Materialien.
Die SIA 262 erlaubt die Umlagerung von Schnittkräften ohne Nachweis des Verformungsvermögens, falls die Druckzonenhöhe begrenzt wird, die Duktilitätsklasse des Betonstahls mindestens B500B ist und die Druckfestigkeitsklasse tiefer als C50/60 ist. Der Eurocode 2 enthält ähnliche Angaben, aber erlaubt hochfesten Beton unter Voraussetzung einer strikteren Begrenzung der Betondruckzonenhöhe. Daraus kann man implizit ableiten, dass Bauteile, die diese Bedingungen erfüllen, als duktil angesehen werden können.
Werden diese Bedingungen nicht erfüllt, gilt es zu überprüfen ob das Rotationsvermögen von erwarteten plastischen Gelenken grösser ist als der Rotationbedarf. Während es kein direkter Nachweis der Duktilität ist, stellt es sicher, dass die plastischen Rotationen, die zur Biegemomentenumlagerung bei Bemessungslast nötig sind, ohne Versagen aufgenommen werden können. In diesem Beitrag zeige und vergleiche ich zwei Methoden um das Rotationsvermögen zu berechnen.
Der Eurocode 2 (2004) schlägt bilineare Zusammenhänge zwischen dem plastischen Rotationsvermögen und xu/d vor, wobei xu die Höhe der Druckzone ist und d die statische Höhe. Die Norm enthält verschiedene Zusammenhänge für normalfesten und hochfesten Beton, und Betonstahl der Klassen B500B und B500C. Die Zusammenhänge dürfen mit einem Faktor multipliziert werden, der der Schubschlankheit Rechnung trägt. Der Hauptnachteil dieser Methode ist, dass es sich um eine «Black Box» handelt, sodass es schwierig für Ingenieure ist die Plausibilität der Resultate zu prüfen.
Sigrist und Marti (1994) schlagen eine allgemein gültige Methode und eine vereinfachte Bemessungsmethode für das Rotationsvermögen vor, die beide auf dem Zuggurtmodell basieren. Bei der vereinfachten Methode wird die mittlere plastische Krümmung bei Versagen mit einer angenommenen Länge des plastischen Gelenks Lpl = d multipliziert (d = statische Höhe). Die Autoren geben zwei analytische Ausdrücke für die mittlere plastische Krümmung an, je nachdem ob Reissen der Bewehrung oder ein Betondruckversagen massgebend wird. Bei tiefen bis moderaten mechanischen Bewehrungsgehalten wird Reissen der Bewehrung massgebend, bei vergleichsweise hohen mechanischen Bewehrungsgehalten das Betondruckversagen.
Die allgemein gültige Methode wird hier nicht im Detail vorgestellt. Sie folgt der gleichen Idee, die Stahlspannungen in der plastischen Zone zu bestimmen. Zusätzlich berücksichtigt sie den Verlauf der Kraft im Zuggurt, der benutzt werden kann, um die Länge des plastischen Gelenks zu bestimmen, und die Biegemomentenumlagerung beim Fliessen des plastischen Gelenks.
Abbildung 2 zeigt einen Vergleich der drei erwähnten Methoden am Beispiel eines Zweifeldträgers unter Gleichlast mit statischer Höhe d = 1200 mm. Das Basisbeispiel wurde mit Beton C30/37, Betonstahl B500B, Schlankheit L/d = 20 (L = Spannweite) und einem Rissabstand sr = 150 mm berechnet. In Abbildung 3 werden diese Parameter einzeln variiert. Die Kurven starten bei der Mindestbewehrung um ein Sprödversagen bei Rissbildung zu vermeiden.
Die bilinearen Kurven des Eurocode spiegeln die Form der Kurven auf Basis des Zuggurtmodells wieder, bei welchen der Knick den Übergang zwischen Stahl- und Betonversagen ausdrückt. Der Unterschied zwischen den beiden Methoden von Sigrist und Marti (1994) bei kleinen mechanischen Bewehrungsgehalten ist hauptsächlich der Abschätzung der plastischen Gelenklänge in der vereinfachten Methode geschuldet: Wenn eine Gelenklänge von Lpl = 0.7 d anstelle Lpl = d angenommen wird sind die Kurven fast identisch. Die unbekannte Länge des plastischen Gelenks ist einer der Hauptnachteile der vereinfachten Methode.
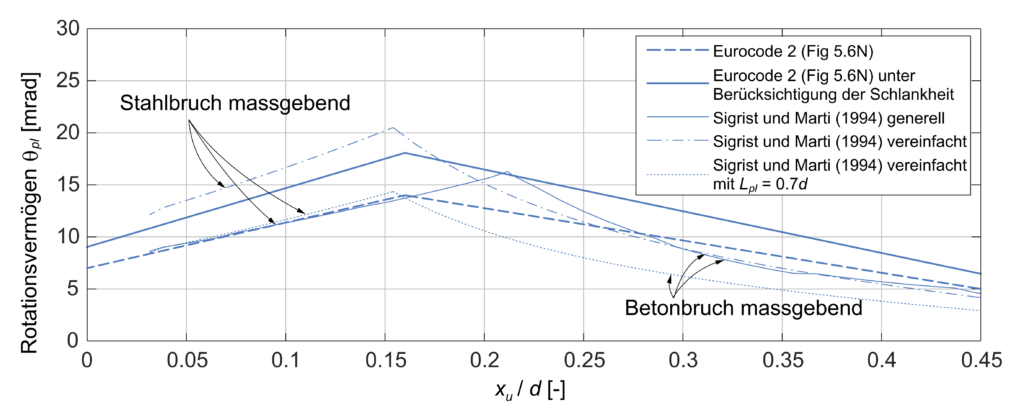
Abbildungen 3 (a) bis (d), zeigen den Einfluss der Betondruckfestigkeitsklasse, der Duktilitätsklasse der Bewehrung, der Schlankheit und des Rissabstandes.
Der Eurocode gibt eine einzelne Kurve für das Rotationsvermögen aller Betondruckfestigkeitsklassen < C50/60 an. Die Modelle basierend auf dem Zuggurtmodell ergeben eine Abnahme des Rotationsvermögens mit höherer Druckfestigkeit, falls Stahlversagen massgebend ist, und kaum einen Einfluss falls Betonversagen massgebend ist. Das mag auf ersten Blick kontraintuitiv scheinen, liegt aber daran, dass die Betonzugfestigkeit laut Zuggurtmodell in direktem Bezug zur Verbundspannung steht. Eine höhere Verbundspannung bedeutet einen grösseren Einfluss der Zugverfestigung und daher eine kleinere mittlere Stahlspannung im Risselement und ein geringeres Rotationsvermögen.
Wird duktilerer Stahl verwendet, so ergeben die Modelle wie erwartet ein grösseres Rotationsvermögen und Betonversagen wird bei tieferen mechanischen Bewehrungsgehalten massgebend.
Laut Eurocode dürfen die bilinearen Zusammenhänge mit einem Faktor kλ multipliziert werden, um die Schlankheit des Bauteils zu berücksichtigen. Die allgemein gültige Methode von Sigrist und Marti (1994) zeigt eine ähnliche Zunahme des Rotationsvermögens mit der Schlankheit, doch die vereinfachte Methode berücksichtigt die Schlankheit nicht.
Die Methoden auf Basis des Zuggurtmodells ergeben, dass ein grösserer Rissabstand einen negativen Einfluss auf das Rotationsvermögen hat. Der bilineare Zusammenhang laut Eurocode berücksichtigt den Rissabstand nicht. Das kann auch als Vorteil gewertet werden, da die Abschätzung der Rissabstände schwierig ist.
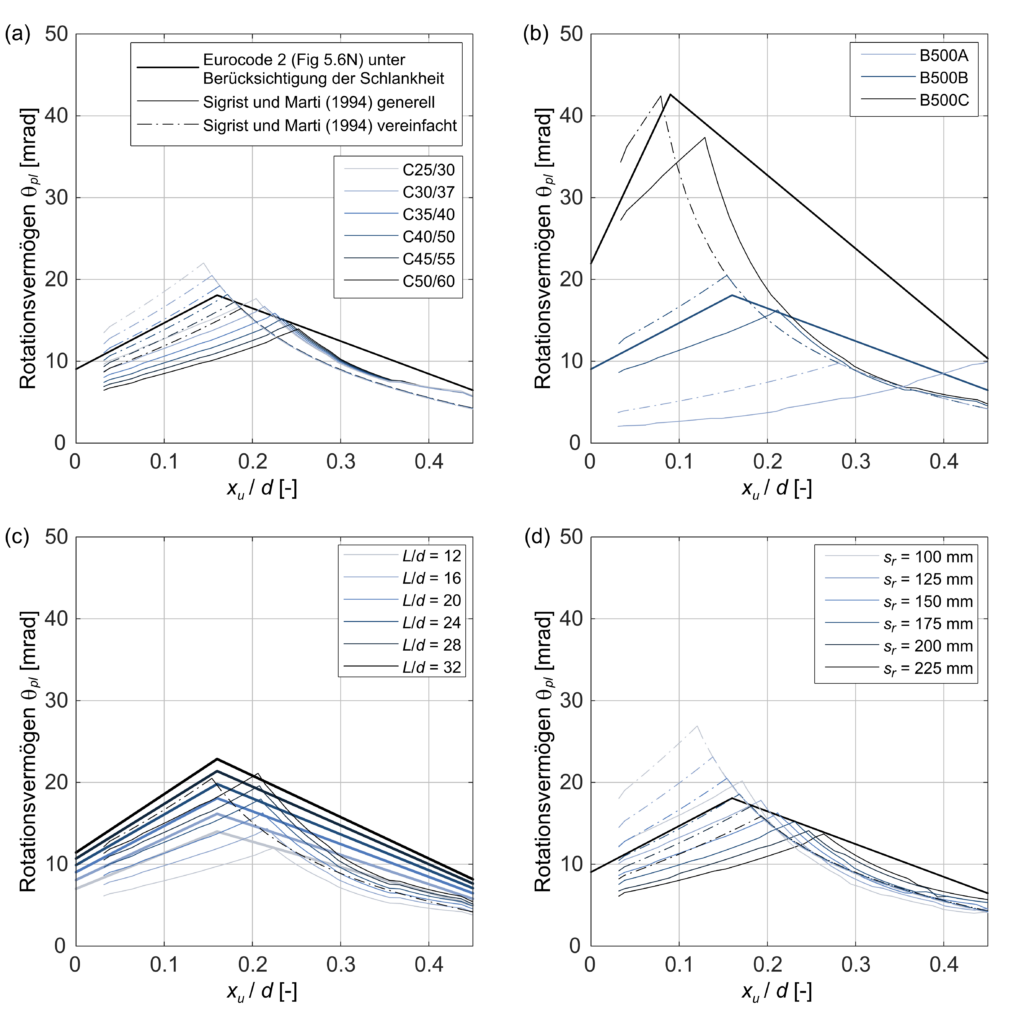
Hier sind die wichtigsten Schlussfolgerungen aus der Parameterstudie zusammengefasst
- Die Länge des plastischen Gelenks hat einen grossen Einfluss auf die Resultate der vereinfachten Methode nach Sigrist und Marti (1994) doch es ist schwierig sie vorgängig zu bestimmen.
- Der Einfluss der Schlankheit wird in der vereinfachten Methode nicht berücksichtigt.
- Der Eurocode gibt tendenziell höhere Schätzungen des Rotationsvermögens, wenn Betonversagen massgebend ist, da der vorgeschlagene Zusammenhang linear ist (im Gegensatz zu den nichtlinearen Kurven der anderen Methoden)
Eine spezifische Bemessungsaufgabe ergibt einen Punkt in den oberen Diagrammen. Da sowohl die Methode nach Eurocode und die vereinfachte Methode nach Sigrist und Marti (1994) sehr einfach anzuwenden sind, macht es Sinn in Praxis beide zu vergleichen.
Die Unterschiede zwischen den Methoden mögen gross scheinen, aber es ist wichtig anzumerken, dass die experimentellen Resultate ebenfalls streuen. Das rechtfertigt es einfachere Methoden beim Nachweis des Rotationsvermögens zu verwenden (anstelle komplizierter Modelle) aber stellt solche Berechnungen grundsätzlich in Frage.
Ein direkter Nachweis der Duktilität (als Verhältnis von z.B. der Rotation bei Versagen und Fliessbeginn) wird bei statischen Problemen nicht praktiziert. Obwohl eine solche Berechnung der Rotationsduktilität in plastischen Gelenken in der Literatur diskutiert wird, gibt es kaum Informationen zu Duktilitätsanforderdungen.
Was ist der Zusammenhang zwischen dem Nachweis des Verformungsvermögens und der Duktilität?
Während Bauingenieur:innen im allgemeinen mit dem Konzept der Duktilität vertraut sind, wird sie oft mit anderen, verwandten Konzepten, wie zum Beispiel dem Verformungsvermögen und dem Verformungsbedarf verwechselt.
Die SIA 260 definiert die Duktilität als Verformungsvermögen, das durch irreversible Verformungen und Engergiedissipation charakterisiert ist, wobei das Verformungsvermögen elastische und plastische Verformungen eines Bauwerks bis zum Versagen umfasst. Ein duktiles Bauteil ist dementsprechend eins, das vor dem Versagen grosse inelastische Verformungen erträgt während es Energie dissipiert, und also nicht entfestigt. Das Konzept der Duktilität ist nicht direkt von den Einwirkungen oder dem Verformungsbedarf abhängig.
Im Gegensatz dazu wird beim Nachweis des Verformungsvermögens laut Eurocode 2 überprüft ob der Verformungsbedarf im Bemessungsfall geringer ist als das Verformungsmögen. Falls die Schnittgrössen insgesamt oder in einer Region gering sind, kann der Nachweis erfüllt sein, obwohl das Verformungsvermögen eines Bauteils gering ist. Das hat positive und negative Konsequenzen. Einerseits scheint es unnötig ein hohes Verformungsvermögen in Bereichen zu bieten, die wohl nie ins Fliessen kommen. Andererseits können unvorhergesehene Lasten oder Eigenspannungszustände zu unerwartet hohem Verformungsbedarf führen, sodass mangelndes Verformungsvermögen fatal sein könnte.
Eine der Hauptschwierigkeiten beim Nachweis des Verformungsvermögens besteht in der Berechnung des Verformungsbedarfs, da er von Eigenspannungszuständen abhängig ist. Das kann anschaulich am Beispiel eines Experiments an einem zweifeldrigen Plattenstreifen gezeigt werden (Abbildung 4). Vor Versuchsbeginn wurde dem anfänglich ebenen Versuchskörper ein Eigenspannungszustand aufgezwungen, indem die Auflager verschoben wurden. Dadurch entsteht die gekrümmte Form bei Last 0 kN in Abbildung 4. Es ist intuitiv klar, dass der Rotationsbedarf am Zwischenauflager in diesem Fall höher ist, als im Fall ohne Eigenspannungszustand. Folglich müssen ungünstige Eigenspannungszustände bei der Bestimmung des Verformungsbedarfs berücksichtigt werden.
Im Extremfall müsste man fordern, dass das Verformungsvermögen grösser ist als der Verformungsbedarf bis zum Erreichen der Traglast. In diesem Fall ist das Verformungsvermögen bei jedem beliebigen Eigenspannungszustand ausreichend. Leider gibt die SIA 262 nicht an, wie genau der Nachweis des Verformungsvermögens erfolgen soll und welche Einwirkungen bei der Bestimmung des Verformungsbedarfs zu berücksichtigen sind.

Was können wir schlussfolgern? Wo soll es hingehen?
In diesem Blogpost wurde das Thema der Duktilität bei der Bemessung von Stahlbetonbauteilen unter statischen Lasten eingeführt und zwei einfache Methoden zur Berechnung des Rotationsvermögens wurden aufgezeigt. Dann wurde der Zusammenhang zwischen dem Konzept der Duktilität und dem Nachweis des Verformungsvermögens erklärt.
Ein Problem ist, dass die SIA 262 keine Methoden bereitstellt um die Duktilität von Bauteilen abzuschätzen, die nicht der gängigen Baupraxis entsprechen. Falls z.B. Bewehrungen benutzt werden sollen, die nicht den Duktilitätsklassen B500B oder B500C entsprechen, können Schnittkräfte nur mit Nachweis des Verformungsvermögens umgelagert werden. Das ist eine schwere Einschränkung für innovative Baumaterialien und Fertigungsprozesse, wie z.B. neue Bewehrungsarten oder die Digitale Fabrikation, da die in den Normen gegebenen Methoden nur für spezifische Anwendungen gedacht sind: Die einfachen Berechnungsmethoden für das Verformungsvermögen sind nützlich für Bauteile die in eine Richtung tragen aber sind z.B. nicht auf Platten anwendbar. Ausserdem ist die Bestimmung des Verformungsbedarfs schwierig, da er von Eigenspannungszuständen abhängt.
Aktuelle Forschung zielt darauf ab eine Strategie zur Bemessung von Bauteilen mit niederduktilen, entfestigenden und spröden Elementen zu entwickeln, wobei das Gesamtbauteil duktil bleiben soll.
Dazu werden die Ideen der Kapazitätstheorie mit elastisch-plastischen System verknüpft und Bauteile so bemessen, dass Versagen in duktilen Bereichen eintritt. Ähnliche Ideen sind die Basis von Normbestimmungen um spröde Schubversagen zugunsten von Biegeversagen zu vermeiden.
Gleichzeitig wird in Zusammenarbeit der Professur für Massiv- und Brückenbau an der ETH Zürich und des Instituts für Bauingenieurwesen (IBI) an der Hochschule Luzern eine Versuchsserie an zweifeldrigen Plattenstreifen durchgeführt.
Abbildung 4 zeigt einen Versuch an einem Plattenstreifen, der mit Betonstahl mit hoher Bruchdehnung aber kaum Verfestigung in einem Grossteil des inelastischen Bereichs bewehrt wurde. Dies ist einer in einer Reihe von 21 geplanten Versuchen mit metallischen Bewehrungen verschiedener Duktilität und Festigkeit, sowie nicht-metallischer Bewehrung.
Die Untersuchungen sollen bei der Verwendung von innovativen Materialien und Fertigungsweisen helfen und das Verständnis, sowie das Bewusstsein für Duktilität, Verformungsvermögen und Verformungsbedarf im Stahlbeton stärken.
Nathalie Reckinger
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to the English version: Fire behaviour of statically indeterminate reinforced concrete structures
Bei Brandversuchen an statisch bestimmten Biegebauteilen (wie einfachen Balken) werden häufig grosse Verformungen beobachtet. Die Verformungen werden zunächst durch den Temperaturgradienten zwischen dem beheizten und dem nicht beheizten Querschnittsrand ausgelöst und später durch die temperaturabhängige Verringerung der Materialeigenschaften verstärkt. Bei statisch unbestimmten Bauteilen werden jedoch Rotationen und/oder axiale thermische Ausdehnungen z. B. an Zwischenauflagern von durchlaufenden Trägern und/oder an Endauflagern behindert. Aufgrund behinderter Rotationen und/oder axialer Ausdehnungen kommt es durch den Temperaturgradienten innerhalb des Querschnitts zu Zwangsschnittgrössen, deren Grösse vom statischen System, der Steifigkeit seiner Bauteile und deren Querschnittswiderstand abhängt.
In Abbildung 1 werden die Folgen einer Brandbeanspruchung an der Unterseite eines statisch unbestimmten, über zwei Felder tragenden Plattenstreifens ersichtlich. Der Plattenstreifen wurde von Kordina and Wesche (1979) getestet. Abbildung 1a zeigt die elastische Biegemomentverteilung (i) bei Raumtemperatur (bezeichnet als Md,el) unter der Annahme einer gleichmässigen Belastung und des Verhältnisses der Bemessungslast bei Raumtemperatur zu derjenigen unter Brandbedingungen von qd / qd,fi = 1,4 und (ii) unter Brandbedingungen (bezeichnet als Mfi) bei verschiedenen Brandeinwirkungszeiten t = [0, 5, 10, 15, 30] min, wobei die tatsächlichen Lasteinleitungspunkte während des Versuchs berücksichtigt werden. Kordina und Wesche geben an, dass der Plattenstreifen so bemessen wurde, dass bei Raumtemperatur 15% des maximalen elastischen Biegemoments vom Mittelauflager zum Feld umgelagert werden müssen (die sich daraus ergebende Biegemomentverteilung entlang der Plattenachse ist in Abbildung 1a mit der gestrichelten Linie angegeben, bezeichnet als Md,pl). Abbildung 1b zeigt das Biegemoment und die Auflagerkraft beim Mittelauflager während der Zeit t im Brandversuch, beide bestimmt durch Kraftmessungen bei den Randauflagern. Die Kurven zeigen, dass positive Krümmungen, die durch die Brandeinwirkung an der Unterseite der Platte verursacht werden, bereits bei kurzer Branddauer zu einem drastischen Anstieg des Stützmoments und der vertikalen Auflagerkräfte am Mittelauflager führen. In Abbildung 1c sind die gemessene maximale Durchbiegung im Feld und eine Abschätzung der entsprechenden plastischen Rotation am Mittelauflager (berechnet auf der Grundlage der Durchbiegungen im Feld) über die Zeit aufgetragen. Sobald das Fliessmoment nach 15 Minuten Brandeinwirkung erreicht war, traten erhebliche plastische Rotationen auf, die nach 90 Minuten fast 120 mrad betrugen und damit die bei Raumtemperatur erwarteten Werte bei weitem übertrafen (vgl. Bestimmungen in der EN 1992-1-1).
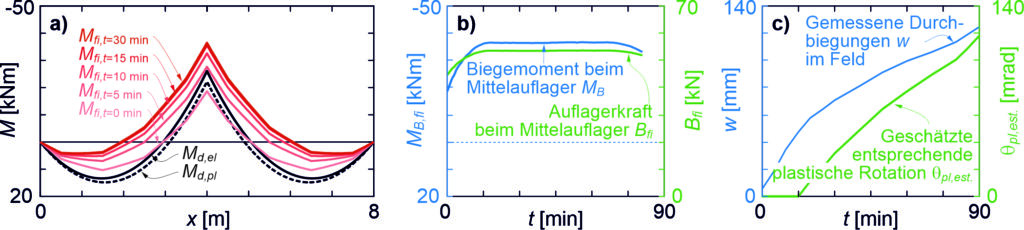
Im Rahmen der Überarbeitung der EN 1992-1-2 zur Bemessung von Tragwerken im Brandfall haben wir mehrere Versuchsserien zu statisch unbestimmten Bauteilen studiert. Dabei haben wir uns hauptsächlich auf die Versuchsserien konzentriert, die vor fast 50 Jahren an der TU Braunschweig unter der Leitung von Prof. Karl Kordina durchgeführt wurden: Ehm et al. (1970) und Wesche (1974) berichteten über mehrere Brandversuche an Durchlaufträgern, während Kordina and Wesche neun Brandversuche an Zweifeld-Plattenstreifen dokumentierten. Abbildung 2 zeigt die Träger 1 und 4 von Wesche nach Versuchsende und Abbildung 3 zeigt die Platten 1, 2, 4, 5 und 9 von Kordina and Wesche nach Versuchsende.


Die Erkenntnisse aus diesen Versuchen an der TU Braunschweig hatten einen direkten Einfluss auf entsprechende Paragraphen zur Bemessung und konstruktiven Durchbildung für statisch unbestimmt gelagerte Träger und Platten in der EN 1992-1-2:
- Bei statisch unbestimmten Trägern und Platten muss die obere Bewehrung ins Feld entsprechend der in Abbildung 4 gezeigten Vorgabe konstruktiv durchgebildet werden. In vier Versuchen von Ehm et al. und vier Versuchen von Kordina und Wesche traten früh im Versuch Risse an den Enden der oberen Bewehrung im Bereich des Zwischenlagers auf, noch bevor direkt am Zwischenlager das Fliessmoment erreicht wurde (siehe Abbildung 3c). Zu einem solchen Versagen kann es kommen, wenn bei der Bemessung der Bewehrung den unterschiedlichen Biegemomentkurven zwischen Raumtemperatur und im Brandfall (vgl. auch Abbildung 1a) keine Beachtung geschenkt wird.
- Bei konstruktiver Durchbildung gem. Abbildung 4 ist die statische Unbestimmtheit bei Trägern im Allgemeinen vorteilhaft, da sie im Vergleich zur statischen Bestimmtheit geringere Achsabstände resp. kleinere Betonüberdeckungen zulässt.
- Bei Anwendung der tabellierten Daten aus der EN 1992-1-2 dürfen für statisch unbestimmte Bauteile maximal 15% der Biegemomente bei Raumtemperatur vom Zwischenauflager zum Feld umgelagert werden. Durch diese Begrenzung unterbindet EN 1992-1-2 indirekt zu niedrige Bewehrungsgrade bei Zwischenlagern.
- Über Zwischenauflager ist bei statisch unbestimmten Plattenstreifen ein Mindestbewehrungsgrad von 0,5% erforderlich, sofern ein begrenztes Rotationsvermögen (durch mangelnde Duktilität der Bewehrung) oder ein erhöhter Rotationsbedarf erwartet wird (Zweifeldplatten).
- Zweiachsig gespannte Platten und axial eingespannte Platten weisen im Allgemeinen in Bezug auf Biegung eine ausreichende Redundanz auf, um einen Einsturz im Brandfall zu vermeiden, wie Wesche (1985) und Wiese (1987) in ihren Dissertationen dargelegt haben. Für Flachdecken verlangt die EN 1992-1-2 (i) leicht höhere minimale Plattenstärken (z.B. h = 200 mm für R90) als für liniengestützte Platten und (ii), für R90 und höher, 20% der oberen Bewehrung im Stützenstreifen von Flachdecken auch im Feld.
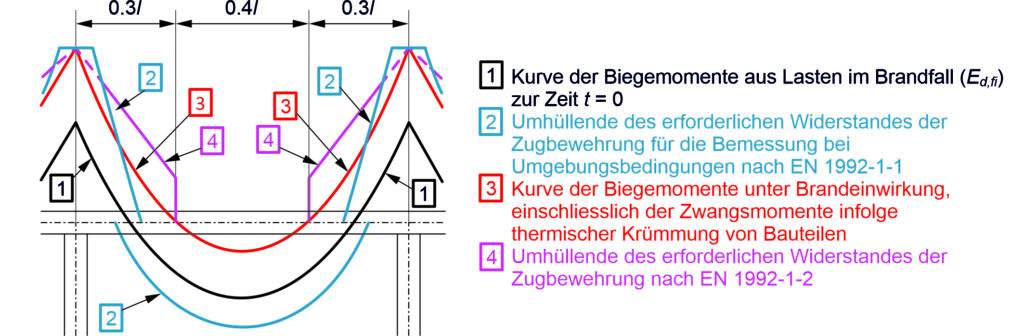
Unter Beachtung dieser Bemessungsregeln können Durchlaufträger gemäss der geltenden Norm EN 1992-1-2 mit geringeren Achsabständen (resp. Betonüberdeckungen) als bei statisch bestimmten Trägern durch Versuchsergebnisse ausreichend abgestützt als sicher angesehen werden. Die Bemessungsregeln für Durchlaufplatten beinhalten jedoch ein beträchtliches Mass an Extrapolation und «engineering judgement», da die experimentellen Grundlagen für Durchlaufplatten spärlich sind: nur drei der neun von Kordina und Wesche geprüften Plattenstreifen erfüllten den zu erwartenden Brandwiderstand unter Verwendung der tabellarischen Bemessungsdaten in der EN 1992-1-2. Dementsprechend ist ein genügendes Rotationsvermögen bei Deckenplatten nicht selbstverständlich – insbesondere dann nicht, wenn weder eine axiale Einspannung mobilisiert werden kann (wie z. B. bei Zwei-Feld-Tunneldecken), noch eine zweiachsige Lastabtragung möglich ist (viele Fertigteildeckenlösungen).
Darüber hinaus sind plastische Gelenke, die durch die hohen Zwangsschnittkräfte unter Brandbedingungen verursacht werden, relevant für die zuverlässige Modellierung des Verhaltens von Stahlbetontragwerken unter (teilweiser) Brandeinwirkung. Daher haben wir ein Modell zur Beurteilung des Verhaltens von biegebeanspruchten Bauteilen unter Brandbedingungen entwickelt. Das Modell baut auf dem Zuggurtmodell auf, das von Sigrist (1995) für die Untersuchung des Rotationsvermögens von biegebanspruchten Bauteilen bei Raumtemperatur entwickelt wurde. Unser Modell basiert auf den thermischen und mechanischen Materialeigenschaften entsprechend der EN 1992-1-2 und einigen ergänzenden Überlegungen zur biaxialen Betondruckfestigkeit und zur Verfestigung der Bewehrung. Das Tragwerk wurde unter Verwendung von damit hergeleiteten Querschnittsmoment-Krümmungs-Beziehungen analysiert, wobei das globale Gleichgewicht und die Kompatibilität durch Iteration sichergestellt wird.
Abbildung 5 vergleicht (a) die Biegemomente MB am Mittelauflager, (b) die maximalen Durchbiegungen wSpan im Feld und (c) die über 100 mm gemittelten Bewehrungsdehnungen εsm,B am Mittelauflager in den von Kordina und Wesche dokumentierten Plattenstreifen. Im Allgemeinen korrelieren die Modellvorhersagen gut mit den Versuchsergebnissen in Bezug auf den Feuerwiderstand, die Entwicklung der Biegemomente am Mittelauflager sowie die Feldverformungen. Der Vergleich zwischen den Versuchsergebnissen und den Modellvorhersagen zeigt jedoch einen beträchtlichen Einfluss der verwendeten Betonzuschläge, der hauptsächlich durch die entsprechende Wärmeausdehnung des Betons verursacht wird.
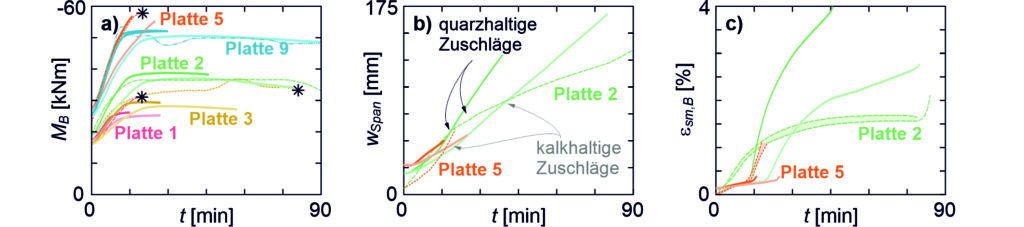
Mit dem entwickelten Modell haben wir eine parametrische Studie durchgeführt mit dem Ziel, (i) die entscheidenden Parameter in Bezug auf das Verhalten von statisch unbestimmten Stahlbetontragwerken unter Brandbedingungen zu identifizieren und (ii) zu diskutieren, ob die in der EN 1992-1-2 angegebenen Bemessungsregeln auch für Platten mit Abmessungen gelten, die nicht denjenigen aus den beschriebenen Versuchsreihen entsprechen. Die parametrische Studie untersuchte die Auswirkungen von Unsicherheiten im Zusammenhang mit der Modellierung statisch unbestimmter Systeme, da nicht nur die Steifigkeit und Festigkeit, sondern auch die Schnittgrössen durch die Verwendung vereinfachter Materialmodelle stark beeinflusst werden. Die folgenden Parameter wurden als die einflussreichsten identifiziert:
- die Duktilität des Bewehrungsstahls (höheres Rotationsvermögen mit höherer Duktilität),
- der Bewehrungsgehalt (höheres Rotationsvermögen mit höherem Bewehrungsgehalt),
- die Betonfestigkeit (höheres Rotationsvermögen mit tieferer Festigkeit) und die Art der Zuschlagstoffe des Betons (Rotationsbedarf mit kalkhaltigen Zuschlagstoffen kleiner als mit quarzhaltigen Zuschlagstoffen) sowie
- die Einspannbedingungen am Bauteilende (günstig für den Brandwiderstand).
Während Projektierende die Duktilität der Bewehrung, den Bewehrungsgehalt und die (charakteristische) Betonfestigkeit vorgeben können, ist es im Allgemeinen nicht möglich, die Zuschlagstoffe in der Planungsphase zu spezifizieren, und die Einspannbedingungen eines Brandabschnitts sind nur schwerlich und ungenau zu quantifizieren. Konzequenterweise konzentrieren sich die Bemessungsempfehlungen der EN 1992-1-2, die hauptsächlich an der TU Braunschweig unter der Leitung von Professor Kordina entwickelt wurden, auf die von Projektierenden beeinflussbaren Eigenschaften.
Auf der Grundlage unserer parametrischen Studie kann davon ausgegangen werden, dass die in der EN 1992-1-2 enthaltenen Bemessungsregeln für praktische Anwendungen allgemein gültig sind. Das Rotationsvermögen ist für die meisten untersuchten Platten mit einem Bewehrungsgrad von 0,5 % ausreichend. Zwar decken die Vorgaben zur konstruktiven Durchbildung nicht alle Eventualitäten ab, wie z. B. das mangelnde Rotationsvermögen bei Verwendung von hochfestem Beton oder grosse Umlagerungen von Querkräften in Richtung von Zwischenauflagern, sie gewährleisten jedoch für die meisten, derzeit in der Praxis angewandten Durchlaufplatten ein genügendes Sicherheitsniveau und sind einfach anwendbar.
Wir konnten mit unserer parametrischen Studie ebenso zeigen, dass die Modellierung von statisch unbestimmten Systemen mit erheblichen Unsicherheiten behaftet ist, wenn (i) die Informationen über das verwendete Material unvollständig sind oder (ii) die angewandten Modelle das verwendete Material nicht oder nur unzureichend beschreiben (z. B. fehlende Verfestigung in der Spannungs-Dehnungs-Beziehung für Betonstahl). Die Betonzuschlagsart mit ihrer entsprechenden thermischen Ausdehnung, die Berücksichtigung der Verfestigungseigenschaften der Bewehrung und der Zugversteifung können bei der Modellierung von statisch unbestimmten Biegebauteilen unter Brandeinwirkung über mehrere Brandwiderstandsklassen entscheiden.
Patrick Bischof
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to the English version: Use of Extended Reality (XR) in Teaching Structural Concrete Design
Für das Verständnis der Inhalte der Vorlesungen im Konstruktiven ingenieurbau sind fortgeschrittenes analytisches Denken und Abstraktionsvermögen unabdingbar: reale (3D-)Strukturen unter verschiedenen Belastungssituationen werden mit Hilfe von rechnerischen Ersatzmodellen für bauweisenspezifische Analysen sowie die Auslegung der Bewehrung untersucht. Insbesondere für Studierende des Bauingenieurwesens mit geringer Berufserfahrung stellt diese Abstraktion in den Vorlesungen eine Hürde dar. Im Stahlbeton kommt erschwerend hinzu, dass die verwendeten Modellvorstellungen die Wirklichkeit wesentlich stärker abstrahieren als in anderen Bauweisen Ein tieferes Verständnis bezüglich der Sachverhalte gewinnen die Studierenden der meist erst in der Reflexion nach der Vorlesung oder in nachfolgenden Übungen und Kollquien. Um den genannten Herausforderungen zu begegnen, entwickeln wir an unserer Professur digitale Demonstratoren und Hilfsmittel zur Unterstützung und Verbesserung der Lehre [1]. Die Hauptideen sind dabei: (i) den üblicherweise papierbasierten Unterricht durch digitale Inhalte zu ergänzen, die über smarte Geräte angezeigt werden; (ii) mobile Technologien zu nutzen, die den Studierenden zur Verfügung stehen, um interaktives, personalisiertes und selbstmotiviertes Lernen anstelle von inhalts- bzw. lehrerzentrierten Anweisungen zu unterstützen; (iii) das Engagement und die Begeisterung der Studierenden für die Vorlesung durch die Immersion in den Vorlesungsinhalt zu steigern, um ein tieferes Verständnis auf individueller Ebene zu fördern; (iv) die traditionellen Lehrmethoden im Bauingenieurwesen zu modernisieren und zu digitalisieren. Zu diesem Zweck haben die Autoren ein mobiles Augmentierte- bzw. Gemische-Realität-Tool (Struct-MRT) [4] konzipiert, implementiert und in Feldstudien unter Studierenden und Lehrenden evaluiert.
Methoden der Erweiterten Realität und deren Einsatz in der Lehre im Bauingenieurwesen
Erweiterte Realität (XR) ist ein Überbegriff für alle Technologien, die reale und virtuelle Umgebungen sowie Mensch-Maschine-Interaktionen kombinieren, die durch Computertechnologie und Mobilgeräte erzeugt werden [2,3]. XR-Technologien schaffen immersive digitale Welten innerhalb des sogenannten Realitäts-Virtualitäts-Kontinuums [2,2] in unterschiedlichem Ausmass je nach Intention, vgl. Abbildung 1. Augmentierte Realität (AR) befindet sich auf der linken Seite des Realitäts-Virtualitäts-Kontinuums in Abbildung 1, wo die reale Welt mit digitalen Inhalten erweitert wird. “Google Glass” oder “Bosch Smartglasses Light Drive BML500P” sind hierbei typische AR-Geräte. Virtuelle Realität (VR) befindet sich auf der rechten Seite des Kontinuums, wobei der Nutzer z. B. über das “Oculus Quest”-Gerät von Facebook in eine vollständig digitale Umgebung eintaucht und die reale Umgebung ausblendet. Gemischte Realität (Mixed Reality / MR) liegt zwischen den genannten Extremen und umfasst alle Technologien, bei denen computergenerierte Inhalte in unterschiedlichen Anteilen mit der Sicht des Einzelnen auf die reale Welt vermischt werden. Das derzeit populärste Gerät für MR ist das “Microsoft HoloLens” Headset.

Derzeit liegen nur wenige Forschungsarbeiten zur Entwicklung und Integration von XR-Technologien in die Bauingenieur-Lehre vor. Es gibt jedoch wissenschaftliche Belege dafür, dass XR das Lernen von abstrakten und schwer verständlichen Themen erleichtert [4 – 6]. Zudem hat die derzeit immer noch herrschende globale Pandemie (COVID-19) viele Hochschulen und Firmen dazu veranlasst, die Art und Weise des Arbeitens, Lehrens und Lernens zu verändern. In unseren prototypischen Studien wurden Inhalte aus verschiedenen Stahlbeton-Vorlesungen als AR Anwendungen für Smartphones und Tablets entwickelt, vgl. Abbildung 2, und als methodische Workflows (Struct-MRT), vgl. Abbildung 3, anderen Lehrenden zur Verfügung gestellt.
Moderne XR-fähige Smartphones und Tablets sind erschwinglich und vielfach bei Lehrenden und Studierenden verfügbar, so dass diese Art von immersivem Unterricht zu geringen Kosten hoch skalierbar ist. Im Rahmen von zwei Feldstudien wurde Struct-MRT bezüglich der beiden Beispielapplikationen einer Stahlbetonkonsole sowie eines Torsionsbalkens im Einsatz in realen Unterrichtssituationen getestet und bewertet, vgl. Abbildung 2 und [1]. Struct-MRT erlaubt den Nutzenden, interaktiv durch die einzelnen Schritte der statischen Berechnung, Bemessung und Bewehrungsführung zu navigieren. Neben der massstabsgetreuen, dreidimensionalen Darstellung der Bauteile werden ergänzende Texte und Formeln dynamisch angezeigt, um den Nachweisprozess zu erläutern. Damit transformieren wir den traditionellen papierbasierten Unterricht in einen immersiven Unterricht, bei dem über mobile Geräte Zugang zu kontextbezogenen visuellen Informationen des Unterrichtsstoffs ermöglicht wird. Komplexe Lehrinhalte der Vorlesungen und Übungen zur statischen Modellbildung oder Konstruktionsdetails können auf diese Weise zusammen mit der konstruktiven, normgerechten Bemessung spielerisch veranschaulicht und erlebt werden. Schliesslich wird mit Struct-MRT ein studierendenzentrierter Ansatz ermöglicht, der individualisiertes und selbstmotiviertes Lernen ermöglicht.
Struct-MRT Workflow einer Übung und Anwendungsbeispiel
Die Interaktionen der Nutzer mit Struct-MRT Applikationen sind in Abbildung 3 (links) als Sequenzdiagramm dargestellt. Während einer Vorlesung können die Studierenden auf die zusätzlichen Inhalte eines Aufgabenblattes zugreifen, indem sie mit ihrem mobilen Gerät (iPhone/iPad) einen QR-Code über die eingebauten Kameras scannen. Wenn sie dann die App auf ihrem Endgerät öffnen, werden computergenerierte 3D-Inhalte einschliesslich Multimedia (z.B. Bilder oder Formeln) angezeigt (vgl. Abbildung 2 und 3). Die Ansichten der entwickelten Anwendungen sind im Vollbildmodus angelegt und unterstützen sowohl die Ausrichtung im Hoch- als auch im Querformat. Zusätzliche grafische Interaktionswidgets werden je nach den Besonderheiten des Einsatzbeispiels entlang des 3D-Inhalts platziert.
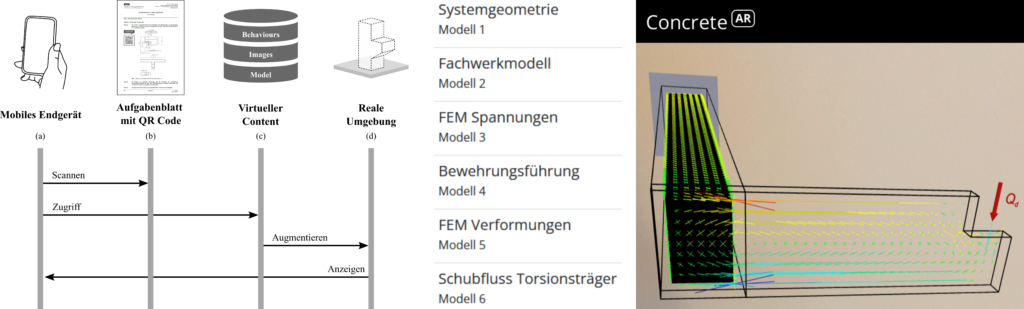
Konkret wurde im vergangenen Herbstsemester eine Übung zur Bemessung und konstruktiven Durchbildung eines Torsionsträgers mit AR Apps angereichert. Die Studierenden konnten neben den papierbasierten Unterlagen sechs AR Applikationen (vgl. Abbildung 3 (Mitte)) parallel dazu nutzen, um räumliche Eindrücke bezüglich der Geometrie des Trägers, der Modellbildung mit Fachwerken oder Spannungs- und Verformungsergebnisse der Finite-Elemente-Methode zu erhalten und in immersiver Weise damit zu interagieren. Nach der Übung wurden die ca. 40 Teilnehmer dieser Feldstudie (Panel) mithilfe eines umfassenden Fragebogens hinsichtlich folgender Ziele befragt:
- Ermittlung der Benutzerfreundlichkeit, des Eindrucks und der Interaktivität.
- Ermittlung des Potentials und der Akzeptanz des Einsatzes von XR in der Ingenieurausbildung und Wissensvermittlung unter den Studienteilnehmern.
- Identifikation möglicher Defizite und Verbesserungspotenziale der MR-Apps.
- Identifikation weiterer geeigneter Anwendungsfälle der MR-Apps.
Im Rahmen der Umfrage wurden folgende Hypothesen getestet:
- H1: Die Vorteile von Mixed Reality sind für die Studierenden leicht zu erfassen
- H2: Der Umgang mit Mixed Reality-Technologien und -Tools ist für Studierende leicht zu erlernen.
- H3: Die Studierenden erkennen die Vorteile von Mixed Reality-Technologien für Lehre und Unterricht.
- H4: Die Studierenden haben Spass an der Arbeit mit Mixed Reality-Technologien und -Werkzeugen
Statistische Hypothesentests zeigen, dass alle vier Hypothesen als zutreffend angesehen werden können. Diese Ergebnisse stützen die Kernannahme der Autoren für den Einsatz von XR in der Lehre: Die die Darstellung von kontextbezogenen 3D-Modellen zur Veranschaulichung der Inhalte ist ein gewinnbringender Ansatz in der Lehre.
Die Studie lieferte weitere Erkenntnisse über die Anwendungsfälle von XR im Bauingenieurwesen. Die grössten Vorteile von XR Applikationen sieht das Panel eindeutig im konstruktiven Ingenieurbau, gefolgt von Bau- bzw. Infrastrukturmanagement. Die Ergebnisse deuten darauf hin, dass die Wahrnehmung und das Verständnis besonders komplexer Struktursysteme mit aufwendigen Entwurfs- und Bemessungsaufgaben durch XR stark unterstützt werden kann. Das Panel gab zudem Hinweise auf weitere unterstützende Funktionalitäten, mit denen künftige Versionen von Struct-MRT Workflows und Applikationen ausgestattet werden können. Weitere Erkenntnisse und statistische Auswertungen dieser Studie können [4] entnommen werden.
Fazit und weitere zukünftige Möglichkeiten
Die Ergebnisse unserer Pilotstudien zeigen zusammenfassend, dass Methoden der Erweiterten Realität im Studien- und Lehralltag noch nicht ausreichend angekommen ist, sich jedoch das Bild einer breiten Akzeptanz dieser Technologie unter Studierenden des Bauingenieurwesens an der ETH Zürich abzeichnet. Die entwickelten Applikationen bieten durch den interaktiven Arbeitsbereich bessere Unterstützung des Lernprozesses und fördern die Interaktion der Studierenden mit den Kursinhalten durch die Immersion in multimedial gestützte Lernumgebungen. Neben dem potenziell transformativen Mehrwert von Erweiterter Realität in der Massivbau-Lehre gaben die Umfragen gleichzeitig einen Einblick in die technologischen, organisatorischen und kognitiven Herausforderungen des Einsatzes in Lehre und Studium. Die Entwicklung und Einführung von Anwendungen aus dem Bereich der Erweiterten Realität ergänzt unser Angebot an digitalen Lernapplikationen und bietet insbesondere Möglichkeiten zu immersiven Lernerlebnissen während der Vorlesung und in den Übungen. Gerne laden wir Sie ein, unsere Applikationen via [1]selbst zu erkunden.
Danksagung
Ein grosser Dank gilt allen Beteiligten, welche zur Umsetzung der Applikationen beigetragen haben und natürlich allen Teilnehmenden der begleitenden Feldstudien.
Projektverantwortliche: Prof. Dr. Walter Kaufmann, Dr. Michael A. Kraus
Applikationen: Irfan Čustović
Beutreuung Tutorien: Simon Karrer
Links
Sammlung aller Stahlbeton-Lernapplikationen: https://concrete.ethz.ch/applikationen/
Literatur:
[1] https://concrete.ethz.ch/blog/lernen-zu-lernen-digitale-lernapplikationen-in-der-stahlbeton-vorlesung/
[2] Milgram, P., & Colquhoun, H. (1999). A Taxonomy of Real and Virtual World Display Integration. Mixed Reality, 5–30.
[3] Osorto Carrasco, M. D., & Chen, P. H. (2021). Application of mixed reality for improving architectural design comprehension effectiveness. Automation in Construction, 126(March).
[4] Kraus, M., Custovic, I., & Kaufmann, W. (2021). Struct-MRT: Immersive Learning and Teaching of Design and Verification in Structural Civil Engineering using Mixed Reality. arXiv preprint arXiv:2109.09489.
[5] Sampaio, A. Z., & Martins, O. P. (2014). The application of virtual reality technology in the construction of bridge: The cantilever and incremental launching methods. Automation in Construction, 37, 58–67. https://doi.org/10.1016/j.autcon.2013.10.015
[6] Shirazi, A., & Behzadan, A. H. (2015a). Content delivery using augmented reality to enhance students’ performance in a building design and assembly project. Advances in Engineering Education, 4(3), 1–24.
Michael Anton Kraus
Kommentieren Sie diesen Post auf LinkedIn oder Instagram
Link to English version: Development of a CFRP-prestressed UHPC bridge system for the SBB
Bei der Suche nach Systemlösungen für Bahnbrücken mit kurzen Spannweiten, wie sie häufig bei Überführungen vorkommen, wird häufig auf die standardisierten «Walzträger in Beton» (WIB) – Brücken zurückgegriffen. Diese sind auf dem Schienennetz der Schweiz weit verbreitet und überzeugen durch eine simple Bauweise, wohlbekanntes Tragverhalten und eine ziemlich sportliche Schlankheit. Als Nachteile sind der hohe Materialverbrauch (Vollplatte mit Stahlprofilen) und die reduzierte Dauerhaftigkeit (exponierte Unterflansche der Stahlprofile) zu nennen. Aufgrund dieser Nachteile strebt die SBB ein alternatives Brückensystem an, welches gegenüber den bisher eingesetzten Systemen verbesserte Dauerhaftigkeitseigenschaften besitzt und eine schnellere Montage ermöglicht. Eine Bestandesanalyse der SBB zeigt den Bedarf eines effizienten und wirtschaftlichen Brückensystems mit minimalem Unterhalt und Streckensperrungen auf: Auf dem SBB-Netz werden ca. 800 bestehende Brücken im Spannweitenbereich zwischen 2 und 10m mit Zustandsklassen 3 (“ausreichend”) oder 4 (“schlecht”) bewertet. Dies bedeutet, dass in absehbarer Zeit Massnahmen an diesen Bauwerken nötig sein werden. Obwohl nicht alle zustandskritischen Brücken ersetzt werden müssen und viele Neubauten als geschlossene Rahmen ausgebildet werden, sieht die SBB einen grossen Bedarf an einfeldrigen Brücken im Spannweitenbereich von 2 bis 10m.
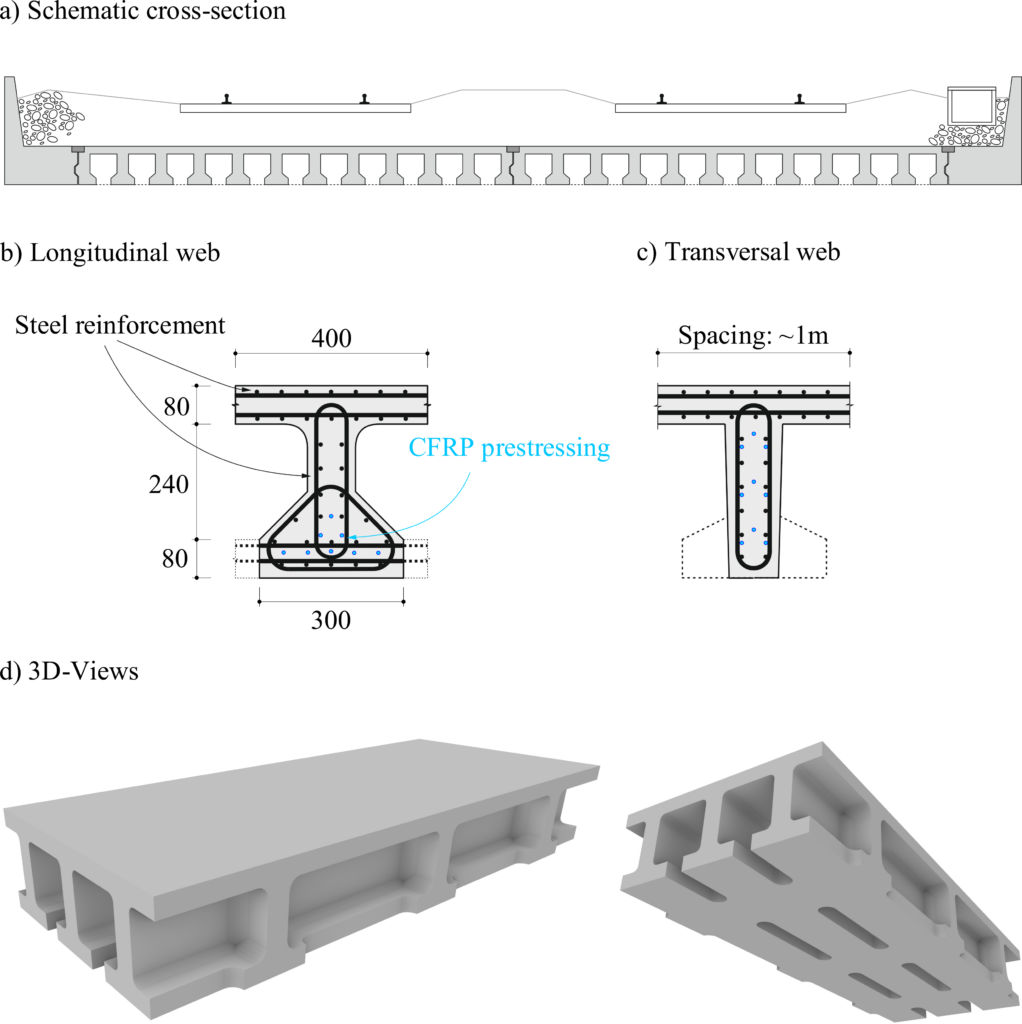
An der Professur für Massiv- und Brückenbau wird unter der Leitung von Prof. Dr. Walter Kaufmann und Dr. Karel Thoma an einer Systemlösung geforscht, welche die oben genannten Nachteile der WIB-Brücken überwindet. Design und Materialisierung sind ganz auf die Dauerhaftigkeit und die schnelle Montage (hoher Vorfabrikationsgrad) ausgelegt. Das Grundkonzept ist in Abbildung 1 dargestellt. Es wird Ultrahochleistungsbeton (UHB) verwendet, welcher durch seine hohe Festigkeit eine schlanke Bauweise ermöglicht und aufgrund seiner Dichtigkeit den Eintrag unerwünschter, korrosionsfördernder Stoffe auf die Bewehrung verhindert. Unter Gebrauchslasten soll das Brückensystem im ungerissenen Zustand verbleiben, wodurch die Durchbiegungen aufgrund der höheren ungerissenen Steifigkeit reduziert werden und sich zudem keine korrosionsförderende Risse bilden. Die Systembrücke wird deshalb in Längs – und Querrichtung vorgespannt. Aus Dauerhaftigkeits– und Überwachungsgründen wird anstelle einer konventionellen Vorspannung aus Stahl ein Kohlenstofffaserverstärkter Kunststoff (CFK) verwendet, welcher im Spannbettverfahren vorgespannt wird. Die CFK-Stäbe werden im Werk in einem Spannrahmen gespannt und zusammen mit konventioneller Bewehrung in der Brückenschalung positioniert (siehe Abb.2), welche anschliessend ausbetoniert wird. Nach dem Aushärten des Betons wird die Vorspannung im Spannrahmen gelöst, womit sich die CFK-Stäbe selber im Beton über Reibung verankern und den Beton auf Druck belasten. Abbildung 2 zeigt schematisch den Prozess der Spannbettvorspannung.
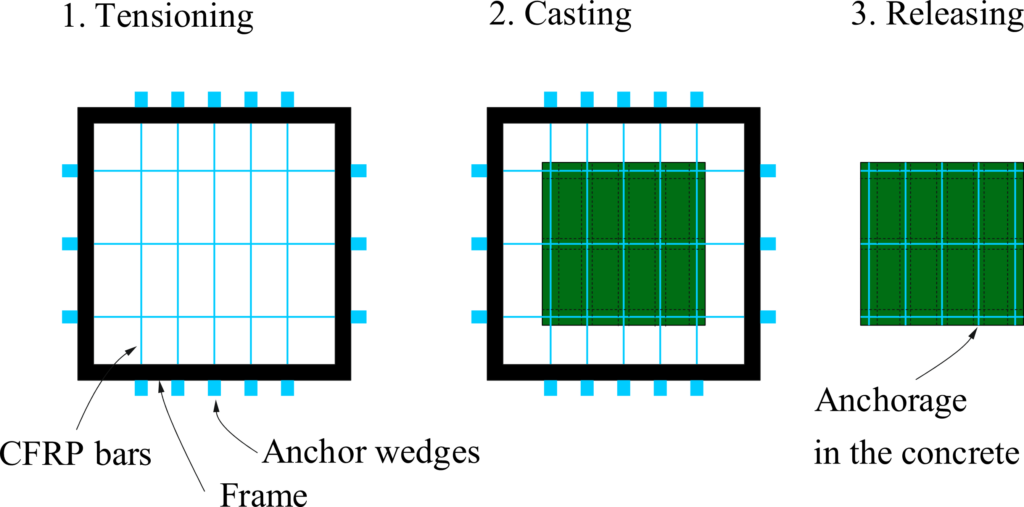
Neben der CFK-Vorspannung wird, wie bereits erwähnt, konventionelle Stahlbewehrung verwendet, welche für ein duktileres Tragverhalten sorgt. Ein System nur mit CFK verhielte sich annähernd linear-elastisch bis zum Bruch. Die gewählte Variante mit einem Unterflansch in Längsrichtung mit Inspektionsöffnungen (Abb. 1 d) erlaubt eine schlanke Bauweise und ermöglicht die Führung der Spannglieder in Längsrichtung im Unterflansch, womit die benötigte Vorspannung minimiert wird und eine Entflechtung mit der Quervorspannung erreicht wird. Nachteile bspw. gegenüber einem offenen Trägerrost ergeben sich bzgl. der visuellen Inspektion im Betrieb sowie in der Schalungstechnik.
Ziel des Projekts ist es, eine zuverlässige Systemlösung zu entwickeln, welche letztendlich vom Bundesamt für Verkehr bewilligt wird. Um dies zu erreichen, müssen als erstes wissenschaftliche Fragen im Zusammenhang mit dem Tragverhalten des Beton-Stahl-CFK-Verbundwerkstoffs, der gemäss Kenntnisstand des Projektteams noch nie für eine Bahnbrücke in der Schweiz verwendet wurde, beantwortet werden. Einen schematischen Überblick über die wissenschaftlichen Fragestellungen gibt Abbildung 3. Ein besonderes Augenmerk wird auf das zyklische Verhalten des Verbundwerkstoffs gelegt: Wie verhält sich das Material nach 1, 2 oder 4 Millionen Lastzyklen im Vergleich zur Erstbelastung? Insbesondere: Wie entwickelt sich das Verhältnis der Verbundspannungen zwischen Bewehrung und Vorspannung (Faktor ξ gemäss SIA 262, 4.3.8.1.5) mit den Lastzyklen? Um diese Fragen zu klären, wird eine gross angelegte Versuchsserie in Zusammenarbeit mit unseren Forschungspartnern an der Empa und der Hochschule Luzern (HSLU) durchgeführt. An der ETH konzentrieren wir uns auf das Verhalten unter Zug (siehe Abbildung 3 a) und die Simulation der Brückenplatte (Abbildung 3 e). Aus den Zugversuchen werden wir ein auf CFK-Vorspannung erweitertes Zuggurtmodell [1] entwickeln, welches das Last-Verformungsverhalten und die Duktilität des Werkstoffs inklusive Effekte aus zyklischer Belastung modelliert. Dieses dient als Grundlage für ein universales Werkstoffmodell, welches wir analog zu [2] in ein nichtlineares FE-Framework implementieren werden um in der Entwicklungsphase eine gross angelegte numerische Parameterstudie für das definitive Design des Brückensystems durchführen zu können. Prof. Dr. Giovanni Terrasi und sein Team an der Empa kümmern sich intensiv um die Spannbettvorspannung und die Entwicklung einer Klemmverankerung für CFK-Vorspannung. Weiter behandeln sie das Verbundverhalten der CFK-Vorspannung im Randbereich des Trägers (Abbildung 3 c), sowie das zyklische Verhalten eines statisch bestimmten Trägers unter Biegung und Querkraft (Abbildung 3 b). Die HSLU unter der Leitung von Prof. Dr. Albin Kenel kümmert sich – neben sämtlichen Fragen zur Betontechnologie, dem systematischen Messen von Materialparametern und Fragen der Nachbehandlung (UHB ist aufgrund seines hohen Zementgehalts sehr schwindanfällig) – um das Design des Spannrahmens, die Lastverteilung in der Brücke bei exzentrischer Laststellung (Abbildung 3 d) und das Brandverhalten.
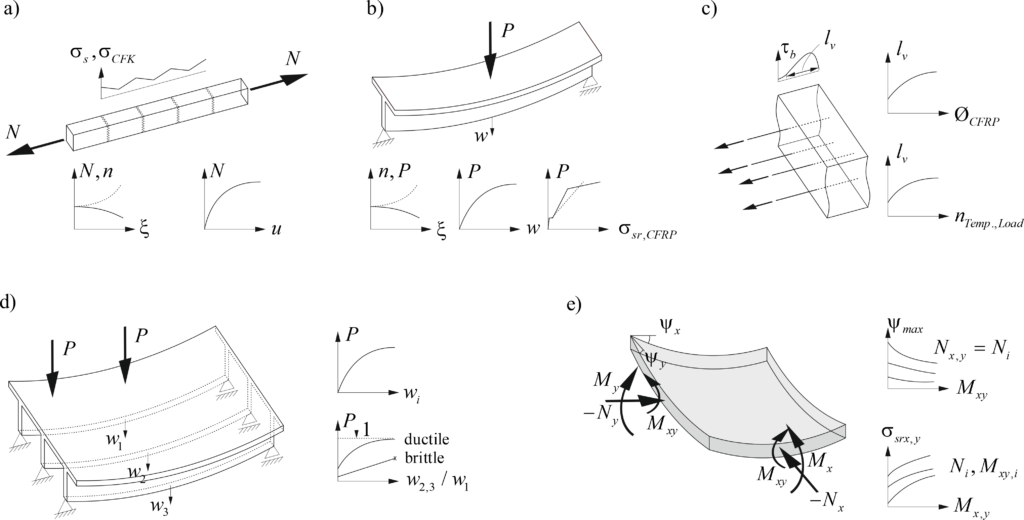
Erster Höhepunkt des Projekts ist ein Grossbauteilversuch an einem 2 x 6 m Ausschnitt einer Brücke. Der Versuch dient als «Proof of concept», der aufzeigen soll, dass (i) wir die Herstellung im Griff haben, und (ii) das mechanische Verhalten einen Einsatz für die SBB grundsätzlich erlaubt. Der Herausforderung, diesen ersten grossen Brückenausschnitt herzustellen, nimmt sich die alphabeton AG an. Unsere Umsetzungspartnerin ist zuständig für die Herstellung sämtlicher Versuchskörper im Projekt. Die Herstellung bringt einerseits einige Herausforderungen bezüglich Schalungstechnik mit sich. Die grösste Challenge ist jedoch die Vorspannung, welche speziell bezüglich Arbeitssicherheit sorgfältige Planung erfordert.
Der Grossbauteilversuch wird im Frühjahr/Sommer 2022 bei uns in der Bauhalle an der ETH Hönggerberg durchgeführt. Über den weiteren Verlauf des Projekts, welcher nach dem «Proof of concept» und der beschriebenen wissenschaftlichen Aufarbeitung das Design der Systemlösung und ein Dimensionierungs-Tool mit anschliessendem Pilotprojekt auf dem Streckennetz der SBB beinhaltet, werden wir Sie hier in unserem Blog auf dem Laufenden halten.
Literature
[1] Alvarez M. Einfluss des Verbundverhaltens auf das Verformungsvermögen von Stahlbeton. Tech Rep 236, Institut für Baustatik und Konstruktion, ETH Zürich;1998. http://dx.doi.org/10.3929/ethz-a-002000033.
[2] Thoma K, Roos P, Weber M. Finite-Elemente-Analyse von Stahlbetonbauteilen im ebenen Spannungszustand. Beton- Stahlbeton 2014;109(4):275–83. http://dx.doi.org/10.1002/best.201300087.
Andreas Näsbom
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to English version: On the emergence of Digital Fabrication with Concrete
Digitale Fertigung mit Beton (DFB) hat sich in den letzten Jahren zu einem neuen Trend in der Bauindustrie entwickelt. Doch woher kommt dieser Trend, und was ist DFB? In diesem Blogbeitrag wollen wir Sie in das Thema DFB einführen und die drängendsten Fragen aus diesem Bereich beantworten.
Was ist Digitale Fertigung mit Beton?
Digitale Fertigung mit Beton beschreibt verschiedene Fertigungsverfahren, bei denen Betonelemente in einem automatisierten Prozess hergestellt werden. Mit diesen Technologien können fast alle Arten von Betonelementen ohne oder mit wenig Schalung und unter Optimierung des Materialeinsatzes hergestellt werden (Wangler et al. 2019). Diese neuen Verfahren behaupten die Bauindustrie effizienter zu machen und die negativen Auswirkungen auf die Umwelt zu reduzieren. Von den unterschiedlichen, derzeit vorhandenen Verfahren ist der 3D-Druck mit Beton (3DDB) das am häufigsten angewandte. Bei 3DDB wird ein Betonelement durch das Auftragen von Schichten additiv hergestellt, wie man es von herkömmlichen 3D-Druckern mit Kunststoff kennt.
Was ist die Geschichte dieser Technologien?
Die erste automatisierte und schichtweise Herstellung eines Betontragwerks geht auf die 1940er Jahre zurück. Mit der Urschel Wall Building Machine wurde ein kreisförmiges Betontragwerk mit einem automatisierten System hergestellt.

Diese Erstentwicklung wurde in den darauf folgenden Jahrzehnten nicht weiterentwickelt oder weiterverwendet. Anfang der 2000er Jahre veröffentlichte Prof. Khoshnevis (Khoshnevis 2004) seine Arbeit zu Contour Crafting (ein 3DDB-System mit seitlichen Taloschen) und löste damit einen Schub in der Forschung und Entwicklung von 3DDB und anderen DFB-Technologien aus. Heute nutzen und erforschen Unternehmen und Institutionen auf der ganzen Welt diese neuen Technologien. Die bekanntesten Anwendungen sind der Einsatz für den Bau ganzer Gebäude, wie z.B. ein kürzlich in Deutschland errichtetes Wohnhaus. Verschiedene DFB-Technologien wurden bei der Herstellung der DFAB-Wohneinheit im NEST-Gebäude der Empa eingesetzt. Die Anwendung von DFB ist jedoch nicht nur auf Häuser beschränkt. Es gibt eine breite Palette von Anwendungen in verschiedenen Bereichen wie künstlerische Installationen, Brücken, Infrastrukturelemente usw. (siehe Abblildung unten).

Was sind die aktuellen Herausforderungen?
Die Weiterentwicklung der DFB-Technologien, insbesondere 3DDB, steht vor verschiedenen Herausforderungen. Forscher und Unternehmen bemühen sich weltweit, diese Herausforderungen zu meistern. Die wichtigsten Forschungsbereiche umfassen Material-, Architektur- und Tragwerksüberlegungen. Auf der Materialebene sind die Eigenschaften im frischen und ausgehärteten Zustand, die Materialzusammensetzung und die Verarbeitung einige der Hauptinteressengebiete. Für Architekten ergeben sich neue Möglichkeiten und Grenzen für die Gestaltung. Der gesamte Gebäudekatalog, einschliesslich der Gebäudetechnik, kann neu gedacht werden, wenn DFB eingesetzt wird.
Eine der grössten Herausforderungen (und der Schwerpunkt der Forschung des Autors) ist die Anwendung von DFB für Tragwerke. Aufgrund des Mangels an Bewehrungskonzepten wurde bei den meisten bisherigen Anwendungen unbewehrter, gedruckter Beton als Mauerwerk-Ersatz oder als verlorene Schalung (d.h. zum Betonieren eines herkömmlichen Stahlbetonbauteils innerhalb der gedruckten Schale) verwendet. Es ist jedoch fraglich, ob 3D-gedruckter Beton (typischerweise mit hohem Klinkeranteil), der als Mauerwerk-Ersatz oder verlorene Schalung verwendet wird, zu einer nachhaltigeren Bauweise führt.
Die Palette von DFB-Bauteilen müsste auf tragende Anwendungen erweitert werden, die denen von herkömmlichem Stahlbeton ähnlich oder gleichwertig sind, um einen bleibenden positiven Einfluss auf die Bauindustrie zu haben. Daher sind neue Bewehrungsstrategien erforderlich. Das Vorsehen von Bewehrung zu DFB und insbesondere zu 3DDB ist jedoch nicht einfach zu bewerkstelligen. Ohne Bewehrung kann ein nach heutigen Normen bemessener DFB nur für Tragwerke eingesetzt werden, in denen nur Druckspannungen vorherrschen, oder für welche keine statische Anforderungen vorhanden sind, oder für welche die Tragsicherheit über Versuche nachgewiesen ist. Es gibt entsprechend keinen Massenmarkt tauglichen Rahmen, der uns sagt, wie wir DFB-Bauwerke auf zuverlässige Weise entwerfen und bauen können.
All diese Herausforderungen müssen angegangen werden, wobei gleichzeitig allgemeine Überlegungen wie sozioökonomische Auswirkungen und Nachhaltigkeit zu berücksichtigen sind. Weitere Einzelheiten zu den aktuellen Herausforderungen der digitalen Fertigung mit Beton werden in verschiedenen Übersichtsartikeln wie (Wangler et al. 2019), (Khan et al. 2020) und (Menna et al. 2020) behandelt.
Was passiert an der ETH Zürich?
Im Jahr 2014 wurde der vom SNF finanzierte NFS Digital Fabrication ins Leben gerufen. Dabei handelt es sich um eine schweizweite “Initiative, die Entwicklung und Integration digitaler Technologien im Bereich der Architektur” vorantreibt (dfab.ch). Das Projekt ist in verschiedene Bereiche unterteilt, die sich mit unterschiedlichen Aspekten der Digitalisierung der Bauindustrie befassen. Einer der Bereiche konzentriert sich auf DFB. Innerhalb dieses Bereiches werden an der ETH Zürich verschiedene Technologien wie Smart Dynamic Casting (Lloret Fritischi 2016), Eggshell (Burger et al. 2020), MeshMould (Hack 2018), KnitCrete (Popescu 2019) und 3DDB (Anton et al. 2020) interdisziplinär untersucht (siehe Abbildung unten).

An der Professur für Massiv- und Brückenbau befassen wir uns mit den tragwerksrelevanten Aspekten dieser neuen Technologien. Wir fragen uns: Wie können wir statisch einwandfrei funktionierende Bauteile bauen? Wie können wir eine Win-Win-Situation bei der Kombination von Bewehrung mit DFB-Verfahren schaffen? Gibt es Bewehrungsansätze, die sich im konventionellen Stahlbeton nicht durchsetzen konnten, aber im Bereich der DFB neue Möglichkeiten bieten könnten? Wie werden wir die Elemente verbinden und wie werden die Lasten übertragen?
Mit einem Team von Doktoranden und PostDocs gehen wir diesen Fragen nach, indem wir Versuchskörper herstellen, diese in unseren Labors testen und, falls nötig, exisitierende Modele anpassen oder neue entwickeln. Die Abbildung unten zeigt einige Beispiele aus unseren aktuellen Forschungsarbeiten.

Wo geht die Reise hin?
Die Träume für DFB-Technologien sind gross: vom Drucken mehrstöckiger Gebäude bis hin zu Kolonien auf dem Mars. Allerdings befinden sich heute die DFB-Technologien noch im Entwicklungsstadium. Es müssen noch viele Herausforderungen bewältigt werden, bevor DFB zu einem festen Bestandteil der Bauindustrie wird. Die Bauindustrie steht in den kommenden Jahrzehnten von einigen grossen Aufgaben. DFB stellt dabei ein spannendes Forschungsgebiet dar, das einen Anteil für die Lösungen liefern wird, wie gross dieser Anteil aber sein wird, wird sich noch zeigen.
Lukas Gebhard
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to English version: Performance-based generative design of network tied-arch bridges
Die Methode des Generative Design (GD) [1] wurde kürzlich auch im Bauwesen eingeführt und markiert einen Wandel in Konzeption, Entwurf und Realisierung der gebauten Umwelt. Die Grundidee hinter GD ist die effiziente Generierung von Entwurfsalternativen ausgehend von einem parametrischen Modell einer baulichen Struktur unter definierten Leistungskriterien und Randbedingungen, sodass den Beteiligten eine informations- und datenbasierte Entscheidungsfindung ermöglicht wird. Zu diesem Zweck stellt die GD eine Methode zur Entwurfsautomatisierung und -optimierung dar, welche seit diesem Jahr ebenfalls in kommerziellen Produkten der Ingenieurpraxis wie AUTODESK REVIT etc. verfügbar ist und bereits erste publizierte Anwendungen vorweisen kann, z. B. [2].
Im Bereich des Bauingenieurwesens stellen Infrastrukturbauwerke und insbesondere Brücken ein potentielles Anwendungsfeld von Generativem Design dar. Andererseits gibt es bis heute keinen ausgereiften durchgehend digitalen und somit rechnergestützten Entwurfs- oder Optimierungsansatz für Brücken, da sich diese Aufgabe durch nichtlineare Interaktionen der Brückenkomponenten und eine enorme Anzahl geometrischer und materieller Entwurfsvariablen sehr komplex gestaltet. Daher ist die Optimierung von Brücken mühsam, zeitaufwendig und stark von der Erfahrung des jeweiligen Ingenieurs bzw. Ingenieurin abhängig. Die kollektive Auswertung von Entwurfserkenntnissen und -mustern wird nur in begrenztem Umfang durchgeführt, eine systematische und methodische Bewertung durch moderne Algorithmen des maschinellen Lernens (ML) ist somit nicht möglich, siehe Abbildung 1 (links).
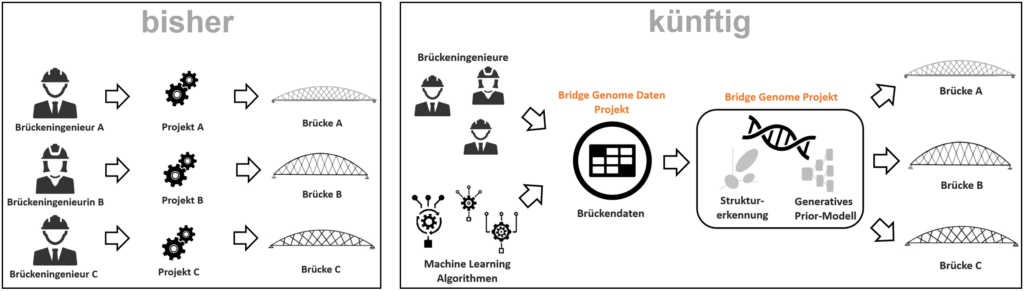
Um das erwähnte Problem beim Brückenentwurfs anzugehen, haben wir das “Bridge Genome Project” initiiert. Darin wird die Forschungshypothese evaluiert, dass der heute verfolge Ansatz beim Entwurf durch den Einsatz moderner ML-Methoden in Verbindung mit Datenbanken über bestehende Bauwerke und GD erheblich unterstützt und verbessert werden kann. Das Konzept zur Erzielung dieser Idee ist in Abbildung 1 (rechts) dargestellt. Die Idee hinter dem “Bridge Genome Project” ist es, Informationen über bestehende Bauwerke zu sammeln, um die zugrundeliegenden Muster des Brückendesigns (das “Design-Genom”) mit ML zu identifizieren. So trainierte ML Modelle dienen dann als Ausgangspunkt für weitere GD-Studien im Zuge neuer Projekte. Zur Überprüfung des Konzepts (proof of concept) werden im Rahmen dieser Studien ausschließlich Netzwerkbogenbrücken untersucht.
Der vorgeschlagene Arbeitsablauf besteht aus den folgenden fünf Schritten, vgl. Abbildung 2:
- Erfassung der Strukturdaten von Brücken in einer Datenbank;
- Durchführung einer Clusteranalyse durch unüberwachte ML-Algorithmen;
- Durchführung von Vorhersagen durch ML-Regressions-/Klassifizierungsalgorithmen, um initiale Brückenmodelle (Priormodelle) zu erstellen;
- Zuführung der Priormodelle der Brücken in den GD-Prozess in Grasshopper / Rhino;
- Optimierung von Entwurfsalternativen mit Grasshopper / Rhino [4].
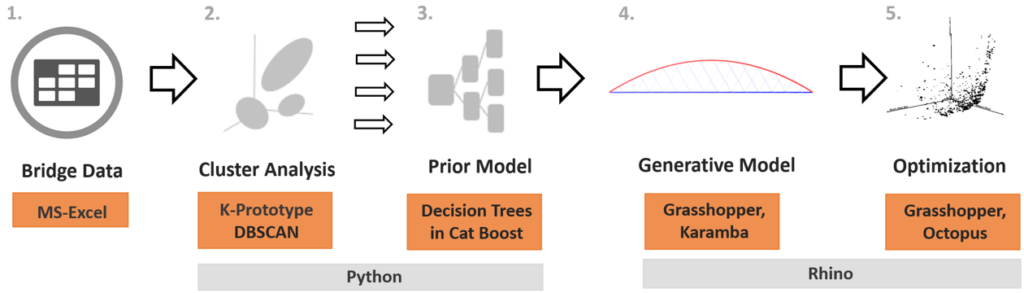
Auf der Grundlage eines vorverarbeiteten Datensatzes von weltweit existierenden Netzwerkbogenbrücken wurde eine Clusteranalyse durchgeführt, um latente Strukturen innerhalb der Brückendaten mit Hilfe von zwei unüberwachten Lernalgorithmen, K-Prototype [5] und DBSCAN [6], zu identifizieren. Beide Algorithmen konnten konsistente Strukturen in den Daten erkennen, z.B. dass eine Ähnlichkeit aller Brückenparameter für Netzwerkbogenbrücken in Abhängigkeit der Spannweiten besteht (siehe Titelbild). Anschließend wird auf den Clustern ein Priormodell trainiert, welches in der Lage ist, geeignete Brückenparameter für neue Projekte in einer vordefinierten Reihenfolge vorherzusagen. Da es sich im vorliegenden Fall um gemischte Datentypen handelt, wird hier der CatBoost-Algorithmus [7] eingesetzt, da dieser gleichzeitig Regressions- und Klassifikationsmöglichkeiten anbietet.
Nach der Generierung von Brückenentwürfen mit diesem Priormodell werden die parametrischen Strukturmodelle zur Optimierung in Grasshopper und Karamba3D in der Rhino 7-Umgebung übergeben. Hierbei kann das generative Modell ein Echtzeit-Feedback bezüglich statischer aber auch weiterer Kriterien für alle Parameteränderungen liefern. Dazu wird das Plug-in Octopus eingesetzt, um mit Hilfe des genetischen Optimierungsalgorithmus HypE die multikriterielle Optimierungen der Brückenparameter durchzuführen. Im Rahmen der hier vorgestellten Studie wurden als Zielfunktionen die Materialkosten, statische Ausnutzung (hier vereinfacht 2D und linear elastisches Werkstoffverhalten angenommen) sowie ein neu entwickelter ML-basierter Prädiktor für die ästhetische Qualität des Brückenentwurfes untersucht. Beispielhafte Ergebnisse der Optimierungen sind in Abbildung (3) dargestellt. Dabei umfassen die Ergebnisse die Berücksichtigung der Kriterien (i) Materialkosten und statische Ausnutzung (Pareto-Front durch grüne Punkte markiert); (ii) Materialkosten, statische Ausnutzung und ästhetisches Empfinden (Pareto-Front durch lila Punkte markiert).
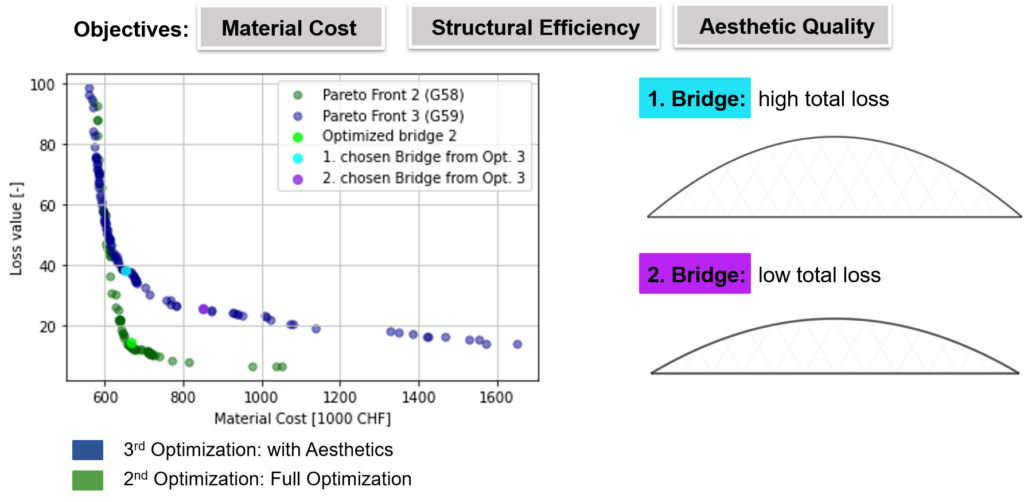
In der hier vorgestellten Proof-of-Concept-Studie zu Netzwerkbogenbrücken erweist sich der entwickelte mehrstufige ML-Ansatz für ein automatisiertes Generatives Design von Brücken als wertvolle Unterstützung des Planenden, insbesondere in frühen Entwurfsphasen eines Projekts. Unser Ansatz ermöglicht einen effizienten statischen Entwurfs- und Optimierungsprozess von Brücken und stellt eine allgemeine Methode zur Verfügung, welche direkt auf andere geeignete Datensätze weiterer baulicher Strukturen wie z.B. Hallen oder Wohngebäude, angewendet werden kann. Der vorgeschlagene ML-Ansatz ermöglicht durch den Clustering-Schritt einerseits die Identifizierung, Extraktion und Analyse von Entwurfsmustern der gebauten Umwelt, welche dann einer weiteren Interpretation und Diskussionen durch Fahleute zugeführt werden kann. Das kalibrierte Priormodell formalisiert dieses Designwissen und ermöglicht die Erzeugung neuer Designs in einem frühen Projektstadium. Die so generierten Entwürfe können dann in die Grasshopper/Rhino-Optimierungsschleife eingespeist werden, um auf automatisierte Weise Leistungsinformationen (z. B. statische Ausnutzungen, Kosten aber auch Ästhetik und Nachhaltigkeit usw.) zu erhalten. Es konnten aber auch Einschränkungen und Kritikpunkte bei diesem Ansatz festgestellt werden. Dies sind die epistemischen Unsicherheiten des Priormodells aufgrund der geringen Größe und Bias des Datensatzes für das Modelltraining. Darüber hinaus ist der Einsatz von Fachwissen und Kreativität eines Bauingenieurs bzw. Bauingenieurin nach wie vor erforderlich, da das maschinelle Lernmodell potenziell ungünstige Entwürfe aus den Daten gelernt haben könnte, Innovationen aufgrund der aktuellen Formulierung des GD-Ansatzes selten vorkommen und die Pareto-Optimalität eine endgültige Stakeholder-Entscheidung über die Abwägung mehrerer Leistungsziele (z. B. Budgetierung vs. statische Ausnutzung usw.) erzwingt.
Dr. Michael A. Kraus
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Literatur
[1] https://www.autodesk.com/solutions/generative-design
[2] https://archistar.ai/blog/4-examples-of-generative-design-in-action/
[3] Kuhn, S. (2021): Parametric Modelling and Generative Design – A Multi-Step Machine Learning Approach for Design and Optimization of Network Tied-Arch Bridges, Master Thesis, ETH Zurich
[4] McNeel, R., & others. (2010). Rhinoceros 3D, Version 7.0. Robert McNeel & Associates, Seattle, WA.
[6] https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html
[7] Dorogush, A., Gulin, A., Gusev, G., Kazeev, N., Prokhorenkova, L., Vorobev, A. (2017): Fighting biases with dynamic boosting, arXiv:1706.09516.
Link to English version: On the fire safety engineering in structural concrete
Ein brennender Raum kann sich in Abhängigkeit seiner Grösse, Belüftung und Brandlast in wenigen Minuten auf über 1000°C erhitzen. Solch eine Brandbeanspruchung verursacht für Stahlbetontragwerke:
- ein differentielles Aufheizen des Bauteilquerschnitts, abhängig von dessen thermischen Materialeigenschaften,
- entsprechende Änderungen der mechanischen Materialeigenschaften (Festigkeit, Steifigkeit) abhängig von der entsprechenden Temperaturverteilung im Querschnitt,
- eine erhöhte Tendenz zu explosiven Abplatzungen in bestimmten Fällen sowie
- Zwangsschnittgrössen und Lastumlagerungen bei statisch unbestimmten Systemen.
Das Verhalten von Stahlbetontragwerken unter Brandeinwirkung wird durch eine Vielzahl von Parametern beeinflusst, hauptsächlich die Brandlast, die Zusammensetzung des Betons und dessen Feuchtigkeit, Spannungen und Dehnungen statischen oder thermischen Ursprungs, die Geometrie und die konstruktive Durchbildung. Abhängig von der Brandeinwirkung, der verwendeten Materialien und des Tragwerks ergeben sich beispielsweise bei Stützen erhöhte Auslenkungen oder bei statisch unbestimmten Systemen veränderte interne und externe Spannungszustände. So waren beispielsweise erhöhte Stützenkopfauslenkungen der Hauptgrund für das Versagen einer Lagerhalle in Gent (1974) (s. Bild), während Kraftumlagerungen zur Innenstütze das Versagen der Einstellhalle in Gretzenbach (2004) (s. Bild) mitverursacht haben.


Oftmals ist es bei Schadensfällen, aber auch bei grossmasstäblichen (repräsentativen) Brandversuchen schwierig bis unmöglich, alle auftretenden Phänomene zu erklären. Bei Schadensfällen kann nach den Löscharbeiten nur mit grossen Unsicherheiten bestimmt werden, welcher Schaden wann aufgetreten ist. Ebenso können bei Brandversuchen nur die Temperatur, Verformungen und äussere Kräfte zuverlässig gemessen werden, um das lokale und globale Verhalten von Versuchskörpern zu diskutieren. Trotzdem konnte dank umfangreicher experimenteller Studien (ergänzt durch theoretische Überlegungen) zum Brandverhalten von Stahlbetontragwerken zwischen 1960 und 1990 (z.B. an der TU Braunschweig unter der Leitung von Prof. Kordina) vergleichsweise einfache Tabellen, konstruktive Regeln und einfach anzuwendende Materialmodelle für Normbrandbedingungen hergeleitet werden. Damit wurde der Nachweis des Feuerwiderstands von Stahlbetontragwerken eine einfache Aufgabe – berechtigterweise, da sich Stahlbetontragwerke im Brandfall bei heute normalerweise verwendeten Querschnittsabmessungen und Bewehrungsüberdeckungen gutmütig verhalten. Das gutmütige Verhalten von Stahlbeton im Brandfall rührt vor allem daher, dass (i) sich Beton vergleichsweise langsam aufheizt und folglich die Bewehrung vor Wärme schützt, (ii) Betonquerschnitte im Vergleich zu Querschnitten anderer Baustoffe massiv sind und (iii) Stahlbeton nicht brennt und folglich selbst nicht zur Brandlast beiträgt. Entsprechend einfach ist der Brandwiderstand von Stahlbetonbauten in den meisten Fällen durch konzeptionelle Entscheide und schnelle Überprüfungen mithilfe von Tabellenwerken gewährleistet (nicht umsonst präsentiert die SIA 262 die wichtigsten Prinzipien zur Brandbemessung auf zwei kurzen Seiten).
Ein gutes Beispiel für das gutmütige Verhalten von Stahlbeton bei hohen Temperaturen ist der Brand des siebengeschossigen Parkhauses der Liverpool Echo Arena (Abmessungen: 70 m x 60 m) im Jahr 2017. Der Brand und die Brandlast in Liverpool waren in ihrem Ausmass beispiellos (bis zu 1400 Fahrzeuge brannten während mehrerer Stunden aus). Das Parkhaus bestand aus Stützen, Trägern, Treppenhauskernen und vorfabrizierten Rippenplatten. Die vorfabrizierten Rippenplatten wurden stark beschädigt resp. stürzten teilweise ganz ein, der Rest des Tragwerks blieb jedoch praktisch unbeschädigt (s. Bild, Referenz: Structural-Safety).

Für die Projektierung oder Überprüfung von Bauwerken mit grossem Schadens- resp. Personenrisiko (z.B. Spitäler, Hochhäuser, Tunnel) und von Bauteilen mit schlanken Abmessungen oder aus neuartigen Betonen sind allerdings Tabellen ungenügend oder gar nicht anwendbar. Um Projektierungsarbeiten für solche Tragwerke oder Bauteile gewissenhaft durchführen zu können, ist ein vertieftes Verständnis für das Brandverhalten von Stahlbetonbauten notwendig. Vor dem Hintergrund der Anstrengungen zur Klimaneutralität kann davon ausgegangen werden, dass über die Anwendung von Tabellen hinausgehende Studien in Zukunft gar vermehrt nötig sein werden, weil:
- der Einsatz alternativer Antriebe wie Lithium-Ionen-Batterien Brandkurven erzeugt, deren Konsequenzen auf Stahlbetontragwerke noch nicht breit studiert wurden (NB: die heutigen Tabellenwerke gelten nur für die Normbrandkurve),
- neue Wege zur materialschonenden Herstellung von Bauteilen und Tragwerken mit entsprechend weniger massiven Stahlbetonquerschnitten gesucht werden (müssen) – wie z.B. mit filigranen Rippentragwerken – sowie
- vermehrt neu entwickelte Betonarten (wie Recyclingbeton, dichte Betone, (ultra)hochfeste Betone etc.) eingesetzt werden (müssen), die eine höhere Wahrscheinlichkeit bzgl. explosivem Abplatzen aufweisen.
Gerade das explosive Abplatzen von vorfabriziertem Beton unter Brandbedingungen hat das Brandingenieurwesen in den letzten 10 Jahren auf den Bürotisch der/des projektierenden Schweizer Bauingenieurin/Bauingenieurs gebracht – und so auch auf meinen Bürotisch beim Start meiner wissenschaftlichen Arbeit in der Gruppe von Prof. Walter Kaufmann an der ETH Zürich. Nach anfänglichen Arbeiten zum explosiven Abplatzen mit der Idee, die Grundlagen für die Korrigenda C1 der SIA 262 im Jahr 2017 zu erweitern, konnten wir in den letzten vier Jahren vor allem im Rahmen der Revisionsarbeiten für die EN 1992-1-2 das Brandingenieurwissen in unserer Gruppe kontinuierlich ausbauen.
Mit dem Wissen um die Relevanz des Brandingenieurwesens unterrichten wir dieses im Stahlbetonbau jedes Jahr im Rahmen der Vorlesung «Advanced Structural Concrete» (Masterstudiengang Bauingenieurwesen der ETH Zürich) und neu auch im Rahmen des MAS-Lehrgangs Fire Safety Engineering (eingeführt und organisiert durch die Professur Holzbau der ETH Zürich). Wir stellen das Material- und Tragwerksverhalten unter Brandbedingungen vor und präsentieren die Anwendung, Stärken und Grenzen der in den Normen verfügbaren Nachweisverfahren. Basierend auf diesem Wissen fördern wir die Fähigkeit, die Plausibilität der mit allgemeinen Berechnungsverfahren bestimmten Ergebnisse zu überprüfen. Darüber hinaus geben wir einen Überblick zur Überprüfung der Brandsicherheit bestehender Bauwerke. Nicht zuletzt wollen wir das Verständnis für die der Norm zugrundeliegenden Annahmen vermitteln, damit zukünftige projektierende Bauingenieure*innen die von der Norm nicht abgedeckten Problemstellungen erkennen.
Patrick Bischof
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Link to English version: Riccardo Morandi – Pioneer of Bridge Design or bad engineer?
Morandi’s Polcevera-Viadukt
Der über einen Kilometer lange Polcevera-Viadukt, gebaut in den Jahren 1963-1967, führte die Autobahn A10 in rund 40 m Höhe über den Fluss Polcevera, die Bahnlinie Turin-Genua, zwei Rangierbahnhöfe und ein Industriegebiet. Die drei markanten, 90 m hohen Pylone im Bereich der rund 220 m langen Hauptspannweiten machten den Viadukt nach seiner Einweihung (zur Bildergalerie) innert Kürze zu einem Wahrzeichen Genuas und einer der bekanntesten Brücken von Riccardo Morandi.
Der damals grösste Viadukt Europas (zum Video) war in verschiedener Hinsicht innovativ, auch wenn Morandi vieles von seiner 1962 fertiggestellten Brücke über den Maracaibo-See in Venezuela übernahm. So sind beispielsweise die Hauptspannweiten beider Viadukte als mehrfeldrige Schrägseilbrücken ausgebildet, ihre Pylone sehr ähnlich gestaltet und die Regelspannweiten bestehen aus vorfabrizierten Elementen. Beim Polcevera-Viadukt verwendete Morandi jedoch erstmals vorgespannte Betonzugglieder als Schrägseile, um deren Steifigkeit zu erhöhen, und die Hauptspannweiten wurden mit Hilfe temporärer Spannglieder frei vorgebaut, was bei den grossen Spannweiten auch heute noch eine Herausforderung wäre.

Durch den hohen Vorfabrikationsgrad und den Freivorbau konnte der Polcevera-Viadukt sehr schnell gebaut werden. Da die Plangenehmigung durch die Bahnbetreiber einige Zeit in Anspruch nahm, dauerte die Ausführung zwar länger als bei der über acht Kilometer langen Brücke über den Maracaibo-See, die in einer Rekordzeit von nur 40 Monaten (!) gebaut wurde. Ohne die genannten Verzögerungen hätten die Hauptspannweiten aber in nur 23 Monaten ausgeführt werden können [1].

Der Polcevera-Viadukt war zudem ein äusserst wirtschaftliches und effizientes Bauwerk, das beispielsweise pro Quadratmeter Brückenfläche nur gerade einen Drittel des (damals teuren) Spannstahls verbrauchte wie die zur gleichen Zeit ausgeführte Bendorfer Brücke, die den Rhein bei Koblenz mit vergleichbarer Hauptspannweite quert. Im Vergleich zur inzwischen fertiggestellten, von Renzo Piano entworfenen neuen Brücke waren der Ressourcenverbrauch und die Treibhausgasemissionen von Morandi’s Polcevera-Viadukt trotz seiner wesentlich grösseren Spannweiten signifikant geringer; Der Ersatzneubau ist durch das gewählte statische System (Aufnahme eines grossen Teils der Lasten als Einfeldträger) und die Querschnittsausbildung (viel Material im Bereich der Neutralachse) statisch ineffizient. Während ersteres durch die notwendige schnelle Montage der einfeldrigen Stahlträger gerechtfertigt werden kann, ist die rein gestalterisch begründete Querschnittsausbildung (sie soll anscheinend an ein Schiff erinnern) schwer nachvollziehbar: Ein statisch effizienter, leichter Querschnitt wäre viel wirtschaftlicher und klimaschonender gewesen und auch für die schnelle Montage vorteilhaft, und hätte gewiss ebenso ansprechend gestaltet werden können.
Einsturz
Vor ziemlich genau drei Jahren, am 14. August 2018, stürzte ein rund 250 m langer Abschnitt im Bereich des westlichen Pylons ein und riss 43 Menschen in den Tod. Nach heutigem Kenntnisstand [2] wurde der Einsturz durch den Bruch eines Schrägseils ausgelöst, was zum Kollaps des gesamten Pylons mit dem zugehörigen Teil des Überbaus, inklusive der angrenzenden Einhängeträger, führte. Das Schrägseil brach dabei nahe der oberen Verankerung infolge gravierender Korrosion, verursacht durch die mangelhafte und teils sogar fehlende Injektion der Hüllrohre in diesem Bereich.
Schwachpunkte des Tragwerkskonzepts
Nach dieser Tragödie kritisierten verschiedene Berufskollegen das Konzept der Brücke und Riccardo Morandi als Ingenieur. Einige der vorgebrachten Kritikpunkte sind dabei schlicht falsch, und zeugen teilweise von mangelnder Fachkompetenz der Kritiker. So wurde beispielsweise angeführt, das Konzept der Brücke sei grundsätzlich schlecht, was man daran erkenne, dass weltweit nur drei solche Brücken gebaut worden seien. Tatsächlich gibt es sehr viel mehr solcher Brücken – sowohl von Morandi als auch von anderen Projektverfassern – insbesondere in Deutschland, wo sie als “Zügelgurtbrücken” bekannt sind. Konkreter wurde bemängelt, dass die Pylone viel zu steif seien, wodurch viele Dilatationsfugen notwendig wurden – offenbar in Unkenntnis der Tatsache, dass mehrfeldrige Schrägseilbrücken entweder steife Pylone oder einen sehr steifen Überbau benötigen [3]. Auch die Ausführung der Schrägseile als vorgespannte Betonzugglieder anstelle nackten Stahls wurde bemängelt, ohne zu realisieren, dass Morandi diese Lösung bewusst gewählt hatte, da durch die Vorspannung des Betons eine rund fünfmal höhere Steifigkeit erreicht wurde als mit dem Spannstahl alleine.
Dass solche für Fachleute offensichtlich falsche Argumente den Weg in die Nachrichten schaffen, geschieht leider nach allen grossen Schadenereignissen, die eine breite Öffentlichkeit interessieren: Journalisten der Tagespresse lassen jeweils nichts unversucht, um möglichst schnell pointierte Aussagen von Experten zu Ursachen und Schuldigen abdrucken zu können. Diese Aussagen stammen aber selten von wirklich kompetenten Fachleuten, da diesen bewusst ist, dass ohne detaillierte Kenntnisse von Objekt und Einsturzhergang (was Wochen oder Monate dauert) über Ursachen höchstens spekuliert werden kann.

Ein Kritikpunkt, der grundsätzlich zutrifft, bezieht sich auf die durch Morandi unterschätzten Langzeiteffekte des Betons, insbesondere des Kriechens. Mit heutigen Berechnungsmethoden können wir relativ gut aufzeigen, dass ein grosser Teil der Vorspannung der Schrägseile des Polcevera-Viadukts im Laufe der Zeit verloren ging, so dass der Beton dekomprimierte und schliesslich riss, wie dies in verschiedenen Zustandsuntersuchungen auch tatsächlich festgestellt wurde. Diese Risse – und das damit einhergehende wechselfeuchte Milieu direkt am Spannstahl – beschleunigten mutmasslich die Korrosion des Spannstahls der Schrägseile. Die Langzeiteffekte verursachten zudem Durchbiegungen des Überbaus, die den Fahrkomfort beeinträchtigten.
In verschiedener Hinsicht entsprach auch das Tragwerkskonzept der Brücke tatsächlich nicht dem heutigen Stand der Technik, insbesondere hinsichtlich Robustheit: Offensichtlich waren die Folgen des Versagens eines einzigen Schrägseils beim Polcevera-Viadukt unverhältnismässig gross. Moderne Schrägseilbrücken werden hingegen so bemessen, dass einzelne Schrägseile ohne Konsequenzen für das Tragwerk ausfallen können. Zudem sind Schrägseile heute mehrfach korrosionsgeschützt und so ausgebildet, dass Schäden frühzeitig erkannt und betroffene Litzen ausgetauscht werden können; beim Polcevera-Viadukt war die Betonüberdeckung hingegen sehr gering, und der Spannstahl war nur teilweise durch Hüllrohre geschützt. Der Durchmesser der Hüllrohre war zudem aus heutiger Sicht für eine zuverlässige Injektion, die wegen der grossen Höhe der Pylone ohnehin sehr anspruchsvoll war, zu klein gewählt. Aufgrund von Korrosionsschäden wurden denn auch bereits 1993 die Schrägseile von zwei der drei Pylone verstärkt – nur der westliche Pylon, bei dem die Korrosion damals am wenigsten fortgeschritten war, wurde nicht verstärkt, was den Einsturz 2018 zur Folge hatte.
Beurteilung
Aus heutiger Sicht beurteilt wies das Tragwerkskonzept des Polcevera-Viadukts also tatsächlich Schwächen auf. War Morandi also kein Pionier des Brückenbaus, sondern vielmehr ein schlechter Ingenieur – wie von einigen Kritikern behauptet? Meine Meinung dazu ist klar: Es ist unfair, ein Bauwerk, das vor mehr als einem halben Jahrhundert gebaut wurde, an heutigen Ansprüchen zu messen. Als Morandi seine Brücken entwarf, wurden Brücken primär an ihren Kosten und an der Bauzeit gemessen – und diesbezüglich war der Polcevera-Viadukt kaum zu übertreffen.
Robustheit war dagegen damals schlicht kein prioritäres Entwurfsziel, so dass Defizite in dieser Hinsicht bei Bauwerken aus dieser Zeit eher die Regel sind als eine Ausnahme. Als Beispiel seien statisch bestimmte Fachwerkbrücken erwähnt, wie sie damals vor allem in Nordamerika üblich waren: Versagt ein einziger Fachwerkstab oder ein Knotenblech, stürzt die gesamte Brücke ein – so geschehen leider im Jahr 2007 bei der Interstate 35W-Brücke über den Mississippi (Baujahr 1967 wie der Polcevera-Viadukt).
Auch hinsichtlich Dauerhaftigkeit weisen sehr viele Brücken aus der damaligen Zeit Probleme auf, da sehr kleine Betonüberdeckungen üblich waren. So sind auch Brücken von zweifellos herausragenden Brückenbauern von schwerwiegenden Korrosionsschäden betroffen, beispielsweise die Crestawaldbrücke von Christian Menn. Einen Vorwurf kann man den Projektverfassern aber kaum machen, da die Problematik der Korrosion durch Chloride damals weitgehend unbekannt war. Erstaunlich ist vielmehr, dass die Betreiber beim Polcevera-Viadukt trotz klarer Anzeichen schwerer Korrosionsschäden keine Massnahmen ergriffen, um den westlichen Pylon zu verstärken – analog zur Verstärkung der anderen Pylone 25 Jahre vor dem Einsturz.
Verbleibt noch die Unterschätzung der Langzeiteinflüsse des Betons, die einen Kritiker gar dazu verleitete zu behaupten, Morandi habe eine gute Intuition gehabt, aber nicht viel Übung im Berechnen (“aveva grandi intuizioni, pero non grande pratica di calcolo”). Diese Kritik ist komplett unangebracht: Aus den Publikationen von Morandi ist ersichtlich, dass er auch analytisch ein Meister seines Fachs war. Dass er die Kriechumlagerungen unterschätzte lag vielmehr daran, dass dieses Phänomen zum Zeitpunkt der Projektierung des Polcevera-Viadukts schlicht noch nicht hinreichend erforscht war [4,5].
Beurteilt man seine Brücken im Kontext der Zeit ihrer Projektierung und Erstellung, bleibt Riccardo Morandi zweifellos der Pionier des Brückenbaus, als der er vor der Tragödie von Genua anerkannt war. Dass seine Brücken nicht an heutigen Massstäben gemessen werden sollen bedeutet aber nicht, dass wir bei der Beurteilung der Tragsicherheit bestehender Bauwerke andere Massstäbe ansetzen dürfen als bei Neubauten: Zwar können die Anforderungen an die Gebrauchstauglichkeit reduziert und Einwirkungen sowie Baustoffkennwerte aktualisiert werden, da sie im Unterschied zu einem Neubau bekannt sind. Ein höheres Einsturzrisiko ist jedoch inakzeptabel. Wird bei der Untersuchung einer bestehenden Brücke ein solch erhöhtes Risiko erkannt, sind vertiefte Untersuchungen, Verstärkungsmassnahmen oder Lastbeschränkungen unumgänglich – so teuer und/oder unpopulär diese auch sein mögen.
Hierin unterscheiden sich Brücken von Autos: Wer einen Oldtimer mit Baujahr 1967 fährt – beispielsweise einen der Alfa Romeo GT1300 Junior auf dem Titelbild dieses Blogbeitrags – nimmt in Kauf, dass sein Fahrzeug weder ABS noch Airbags hat, ja nicht einmal ein Zweikreisbremssystem (das Alfa Romeo erst 1968 beim 1750 GT Veloce anbot). An ein solches Fahrzeug die gleichen Ansprüche wie an ein modernes Auto zu stellen oder gar moderne Sicherheitssysteme nachzurüsten, käme wohl kaum jemandem in den Sinn.
Walter Kaufmann
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram
Literatur
[1] Morandi, R.: “Il Viadotto Polcevera dell’Autostrada Genova-Savona,” L’Industria Italiana del Cemento, No. 12, 1967, pp. 849– 872.
[2] Nutini, A.M, Rapporto della giudice per le indagini preliminari, 22.12.2020, 476 pp.
[3] Virlogeux, M., “Recent evolution of cable-stayed bridges,” Engineering Structures, Vol. 21, 1999, pp. 737–755
[4] Einfluss von Kriechen und Schwinden des Betons auf die Schnittgrößen und Spannungen, TH München, 1966
[5] Trost, H., “Folgerungen aus Theorien und Versuchen für die baupraktische Untersuchung von Kriech- und Relaxationsproblemen in Spannbetontragwerken”, IABSE Symposium Madrid, Vol. 5, 1970
Link to English version: International exchange during the pandemic
Unsere Gruppe kann durch Austauschforscherinnen in vielerlei Weise profitieren. Die tägliche Zusammenarbeit mit ausländischen Forscherinnen ist laut Dr. Jaime Mata Falcón der beste Weg, um unseren Kopf und unseren Forschungshorizont offen zu halten. Wir gewöhnen uns damit an ein globales Leben und die globale Wirtschaft. Ein internationaler Austausch von Forschungsideen und -methoden bietet zudem ein enormes Potenzial für Synergien und Fortschritt. Publikationen sind die klassischste Kommunikationsform in der Forschung. Obwohl sie ein wesentlicher Schritt des Teilens sind, neigen Veröffentlichungen dazu, unpersönlich zu sein und keinen hohen Dialog und keine Interaktion mit unseren Kolleginnen zu fördern. Die Zusammenarbeit mit Auslandsforscherinnen über längere Zeit schafft ein gemeinsames Verständnis sowohl auf persönlicher als auch auf beruflicher Ebene, und es wird eine tiefere Interaktion ermöglicht. Dies ist eine hervorragende Gelegenheit, unsere Ideen effizienter zu verbreiten, neue Perspektiven einzunehmen und langjährige Kooperationen aufzubauen. Während wir uns an die virtuelle Arbeit und Interaktion gewöhnen, bin ich überzeugt, dass diese Ergebnisse nur erreicht werden können, wenn man die Möglichkeit hat, einige Zeit von Angesicht zu Angesicht zu arbeiten und den anderen und seine Kultur kennenzulernen.
Leider hat die anhaltende Covid-19-Pandemie die Interaktion mit ausländischen Forscherinnen, die einige Zeit bei uns verbringen, erschwert. Um mehr Einblick in dieses Thema zu bekommen, teilen drei Austauschforscherinnen in diesem Beitrag ihre beruflichen und persönlichen Erfahrungen und wie diese von der Pandemie betroffen sind.
Erzähl uns von dir!
Ich bin Tobias Huber und komme aus Wien, Österreich. Ich bin 32 Jahre alt und arbeite als Postdoc im Bereich Betonbau. Mein Doktoratsstudium habe ich 2019 an der TU Wien abgeschlossen und meine Doktorarbeit beschäftigt sich mit dem Tragverhalten alter Betonbrücken. Seit geraumer Zeit versuche ich mit meiner Forschung neue Wege für schnelleres und nachhaltiges Bauen zu finden. Neben der Forschung liebe ich es, die Welt zu bereisen, Fußball zu spielen und außerdem bin ich leidenschaftlicher Vespa-Fahrer.
Mein Name ist Laura Esposito und ich bin 28 Jahre alt. Ich komme aus Italien und habe 2018 meinen Master-Abschluss in Bau- und Geotechnik an der Universität Neapel Federico II abgeschlossen. Nach dem Abschluss entschied ich mich, meine Karriere an der Universität mit einem Doktorat fortzusetzen. Das Thema meiner Forschung lautet: Innovative Strukturen durch die Umsetzung von 3D-Drucktechnologie in der Bauindustrie. Die Doktorarbeit ermöglicht es mir, sehr innovative Themen zu untersuchen und herauszufinden, wie sehr Automatisierung in allen Bereichen, einschließlich des Bauingenieurwesens, an Bedeutung gewinnen.
Mein Name ist Lisbel Rueda García und ich bin 29 Jahre alt. Nachdem ich 2017 meinen Master in Bauingenieurwesen an der Polytechnischen Universität Valencia UPV (Spanien) abgeschlossen hatte, schrieb ich mich als Doktorandin in Bauingenieurwesen ein. Meine Forschung konzentriert sich auf das Schubtragverhalten von Betonverbundträgern. Außerdem beschäftige ich mich auch mit dem Tragverhalten und der Ertüchtigung von Betonkonstruktionen unter Erdebenbeanspruchung.
Was machst du an der ETH Zürich?
(Tobias) Ich arbeite am NCCR-dfab-Projekt, einer herausragenden Schweizer Forschungsinitiative für digitale Fabrikation in Architektur und Bau. In einem interdisziplinären Team finden wir Wege, die Technologie des 3D-Drucks für Schalungen von Stahlbetonbauwerken zu nutzen. Mit dieser, durch Roboter ermöglichten, Formfreiheit ist es möglich, nicht nur Materialkosten und Arbeitsaufwand beim Schalungsbau zu senken, sondern auch die Konstruktionselemente zu optimieren. Dies führt zu einem geringeren Materialverbrauch. Wir werden versuchen, das Potential zu zeigen, indem wir einen Demonstrator einer Deckenplatte bauen.
(Laura) Während meines Doktorates hatte ich die Möglichkeit, prägende und spannende Erfahrungen in ganz Europa zu sammeln. An der ETH Zürich konzentriere ich mich zusammen mit meinem italienischen Tutor (Costantino Menna) und meinem Tutor an der ETH (Jaime Mata Falcón) auf Bewehrungsstrategien und deren Wirksamkeit in 3D-Betondruckstrukturen. Ich und Lukas Gebhard (ein ETH-Doktorand, derzeit an meiner Heimatuniversität) arbeiten zusammen und teilen experimentelle Ergebnisse, Fachkenntnisse und Know-how. Die Möglichkeit zu einem direkten Austausch mit einem ETH-Forscher war ein wesentlicher Grund für meinen Austausch. Darüber hinaus ermöglicht mir diese Erfahrung, mit einer der führenden Universitäten in der wissenschaftlichen Forschung zur Digitalen Fabrikation zusammenzuarbeiten.
(Lisbel) Von den spanischen Ministerien werden Stipendien zur Unterstützung von Auslandsaufenthalten vergeben, um die Zusammenarbeit mit einer anderen Universität im Forschungsprojekt und die berufliche und persönliche Entwicklung des Doktoranden an einer anderen Universität zu fördern. Dank dieser Unterstützung bin ich derzeit für drei Monate an der ETH, um die von mir am UPV getesteten Träger mit der Software IDEA StatiCa Detail, die auf der an der ETH entwickelten Compatible Stress Field Method (CSFM) basiert, numerisch zu modellieren.

Wieso hast du dich für die ETH Zürich entschieden?
(Tobias) Zu Beginn meines Doktoratsstudiums im Jahr 2016 hatte ich die Möglichkeit, an einem fib-Workshop zum Thema Schubtragfähigkeit von Betonbauwerken an der ETH-Zürich (Hönggerberg) teilzunehmen. Dort durfte ich Prof. Kaufmann und sein Team sowie die beeindruckende Bauhalle der ETH kennenlernen, welche als Gastgeber fungierten. Mir war sofort klar, dass die ETH Zürich und das IBK meine erste Adresse sein würden, wenn ich jemals die Chance hätte, im Ausland zu forschen.
(Laura) Meine Wahl hängt zweifellos damit zusammen, dass die ETH Zürich eine der führenden Universitäten im Bereich Digital Fabrikation ist. Die wissenschaftliche Forschung an der ETH wird dank der vielen Gruppen in hochmodernen Labors (wie dem Robotic Fabrication Lab) vorangetrieben. Darüber hinaus habe ich die Möglichkeit, meine Forschung zu einem der aktuellsten Themen in meinem Bereich zu verbessern: wie man 3D-betongedruckte Strukturen bewehrt.
(Lisbel) Schon vor der Pandemie, war es nicht einfach, einen Ort zu finden, an dem man ein Thema bearbeiten kann, dass die eigene Forschung verbessert, und zugleich Unterstützung durch einen Betreuer hat. Mit der Covid-Pandemie war es durch die Reisebeschränkungen noch schwieriger, den richtigen Platz zu finden. Jemanden an der ETH zu kennen – in meinem Fall Dr. Jaime Mata Falcón, der meiner Heimatuniversität angehörte – kann diese Suche erleichtern. Dies und die Tatsache, dass sie eine der renommiertesten Hochschulen im Bauingenieurwesen ist, machte die ETH zur perfekten Destination.

Lisbel bei der Salginatobel Brücke
Was ist der grösste Unterschied zu deiner Heimat-Universität?
(Tobias) Die Gruppe von Prof. Kaufmann ist etwa dreimal so groß wie unser Institut in Wien, was die Zahl der dort tätigen wissenschaftlichen Mitarbeiter angeht. Sie haben also eine große Vielfalt in ihren Forschungsthemen, was zu einem sehr fruchtbaren wissenschaftlichen Austausch führt, der aktiv gefördert wird. Sie organisieren zum Beispiel ein zweiwöchentliches Format namens Journal Club, in dem interessante Artikel und Fachbeiträge gemeinsam diskutiert werden. Dadurch bekomme ich viele neue Aspekte für meine eigene Arbeit.
(Laura) Alles an der ETH ist wirklich gross, etwa die Anzahl der Labore und Laborgeräte. Nicht zuletzt auch die Zahl der Personen, die in der Gruppe von Prof. Kaufmann tätig sind, und die Zahl der bearbeiteten Themen. Diese Faktoren sind grundlegend für das wissenschaftliche Umfeld, in dem experimentelle Aktivitäten, kontinuierlicher Austausch und Diskussion im Mittelpunkt stehen.
(Lisbel) Den größten Unterschied habe ich auf jeden Fall in der Teamatmosphäre gemerkt und diese werde ich wahrscheinlich am meisten vermissen. Im großen Forschungsteam von Prof. Kaufmann wird das Teilen von persönlichen Perspektiven gefördert. Die in privaten Unternehmen durchaus übliche Interaktion zwischen Menschen und Teams ist in der akademischen Forschung nicht immer gegeben. Ein Doktoratsstudium ist ein relativ langer Abschnitt in unserem Leben. Es ist sowohl auf persönlicher als auch auf beruflicher Ebene bereichernd, diese Etappe in einer Teamatmosphäre durchzuführen. Darüber hinaus schafft der Ideenaustausch wichtige Synergien.
Welchen Einfluss hatte die Pandemie auf deine Zeit an der ETH Zürich?
(Tobias) Meine Zeit hier begann offiziell im April 2021. Da die Zahl der Covid-Fälle in Wien im Februar/März gestiegen war, musste ich spontan etwas früher als geplant nach Zürich reisen, um eine Quarantäne zu vermeiden. Die Einschränkungen und die Fallzahlen in Zürich waren damals im Vergleich zu Österreich geringer, was das tägliche Leben auch recht entspannt machte. Zum Glück durfte ich auch einige Zeit am Hönggerberg verbringen. Darüber hinaus organisierte die Kaufmann-Gruppe virtuelle Kaffeepausen, was bei der Kontaktaufnahme sehr half.
(Laura) Ich freue mich sehr, hier zu sein, auch wenn dies keine leichte Phase ist. Wir alle erleben jetzt die Covid-Pandemie, die unseren Alltag beeinflusst. Trotzdem kann ich mit Schutzmaßnahmen das Campusleben, die Forschungs- und Laboraktivitäten und die Wunder dieses Landes genießen.
(Lisbel) Natürlich wurde das gesellschaftliche Leben in und außerhalb der Arbeit durch die Pandemie eingeschränkt. Die Tatsache, dass mir trotz Pandemie die Teamatmosphäre an meinem Aufenthalt gefallen hat, zeigt, dass die Gruppe durch neue Technolgien in Kontakt blieb. Obwohl ich viele Kollegen nicht persönlich treffen kann, werden regelmäßige virtuelle Treffen abgehalten, um berufliche und außerberufliche Themen zu besprechen, sodass Sie trotz der bestehenden Einschränkungen Kollegen sehen und von ihnen lernen können.

Was nimmst du aus dieser Erfahrung mit?
(Tobias) All diese Erfahrungen, die ich an der ETH gemacht und Neues gesehen habe, sind nun in meinem „wissenschaftlichen Rucksack“ verpackt. Ich bin überzeugt, dass dies meine zukünftige Forschung insgesamt verbessern wird. Mein Ziel ist es, zumindest einen Artikel über meine Experimente zu schreiben. Noch wichtiger finde ich jedoch dieses neue Netzwerk, das ich hier aufbauen konnte. Ich denke, dies wird zu erfolgreichen zukünftigen Kooperationen zwischen der ETH Zürich und der TU Wien führen.
(Laura) Die Auslandserfahrungen sind von beruflicher und persönlicher Seite wirklich prägend. Es ist wichtig, andere Kulturen, Lebensstile oder Traditionen zu kennen, um eigene und neue Facetten zu entwickeln, zu entdecken und zu schätzen. Hier an der ETH Zürich ist das einfacher, denn es ist wie eine kleine Stadt, in die Studierende aus allen Teilen der Welt kommen, um zu lernen und zu teilen.
(Lisbel) Diese Zusammenarbeit hat es mir ermöglicht, neue Leute zu treffen, die in meinem Forschungsgebiet tätig sind, was ich in Zeiten ohne Konferenzen zum Netzwerken sehr schätze. Der Aufenthalt an der ETH wird meinen Lebenslauf bereichern, ohne dabei meine Heimatuniversität abwerten zu wollen, da ich der Meinung bin, dass das an der UPV erworbene Wissen andere hoch angesehene Universitäten ebenwürdig ist. Andererseits haben die Arbeiten während dieses Aufenthaltes zu sehr interessanten Forschungsergebnissen geführt und eine Verbindung zwischen meiner Heimatuniversität und der ETH geschaffen, die zukünftige Kooperationen begünstigen könnte.

Was war einzigartig während deiner Zeit an der ETH Zürich?
(Tobias) Die sehr hilfsbereiten und netten Leute hier am IBK und generell in der Schweiz. Ich würde mich freuen, mit meinen neuen Kollegen über die Jahre in Kontakt zu bleiben – nicht nur für Forschungsaspekte.
(Laura) Die Verbindung zwischen der Stadt Zürich und den Grünflächen. Auch hier, auf dem Hönggerberg, gibt es einen fantastischen Kontrast zwischen der Innovation und Technologie der ETH und der ländlichen Umgebung draußen.
(Lisbel) Die Menschen, die ich hier kennengelernt habe und die tollen Orte, die ich in der Schweiz besucht habe. Trotz des kurzen Aufenthalts habe ich das Gefühl, Freunde fürs Leben gefunden zu haben, mit denen ich meinen zukünftigen Doktortitel in Zürich oder in Valencia feiern kann.

Welcher kultureller Unterschiede warst du dir nicht bewusst?
(Tobias) Ich wusste, dass Fondue in der Schweiz ein Nationalgericht ist und ich habe es mir oft schmecken lassen. Was ich nicht wusste ist, dass es üblicherweise nur in der kalten Jahreszeit gegessen wird. Immer wenn ich einem Schweizer erzählte, dass ich Fondue gegessen habe, meinten sie, dass es eigentlich nicht die richtige Jahreszeit dafür sei, außer im Kanton Wallis ;-).
(Laura) Auch an Werktagen nach Büroschluss können die Menschen Freizeit und Freiraum genießen: Wanderungen, Spaziergänge um den See, Freizeitaktivitäten werden perfekt in den Alltag integriert.
(Lisbel) 1. Die Leidenschaft fürs Wandern und wie fit die Menschen deshalb sind, was bei diesen beeindruckenden Landschaften durchaus verständlich ist. 2. Die Mittagszeit gegen 12 Uhr statt 14 Uhr, was ich am Ende viel besser fand. 3. Die Schweizer anfangs nicht sehr offen ercheinen, sich aber nach nur einem einzigen Treffen ausserhalb der Arbeit die Beziehung zu einer wirklich guten Freundschaft wandelt.

Tobias Huber, Laura Esposito und Lisbel Rueda García
Link to English version: The way to the automatic crack measurement in experiments on the load-bearing behaviour of concrete
Vor knapp fünf Jahren konnte ich im Rahmen einer Master-Projektarbeit erste Methoden für ein Rissmessungs-Tool zur Auswertung von Betonversuchen entwickeln. Das Ziel dabei war, aus den Messungen der Oberflächenverformung, die durch digitale Bildkorrelation gewonnen werden, automatisch Risse zu erkennen und deren Weite und Schiebung zu messen. Meine Betreuer Prof. Dr. Walter Kaufmann und Dr. Jaime Mata-Falcón hatten zu diesem Zeitpunkt bereits erste Ideen und Konzepte ausgearbeitet und auch einige Testdaten standen zur Verfügung. Nach Abschluss der Projektarbeit wurde das Tool stetig weiterentwickelt und vermehrt auch zur Auswertung unserer Versuche angewendet. Dabei zeigte sich das grosse Potential des Verfahrens, sodass es heute als Open-Source-Software unter dem Namen ACDM (für «automated crack detection and measurement») frei zur Verfügung steht. Die Benutzeroberfläche bietet eine einfache Anwendung, so dass auch bereits andere Forschungsinstitute auf dieses Tool zurückgreifen. In diesem Blogbeitrag geht es um den Weg zum heutigen ACDM, dessen Bedeutung in der experimentellen Forschung sowie um die wichtigsten Elemente, die dem Tool zum Durchbruch verhalfen.
Weshalb sind Rissmessungen in Versuchen so wichtig?
Um das Tragverhalten von Betonelementen besser zu verstehen und Modelle weiterentwickeln und validieren zu können, sind Belastungsversuche nötig, bei welchen das Rissverhalten genau erfasst wird. So ist zum Beispiel die Schubkraft, die über Risse übertragen werden kann, stark von der Unebenheit der Rissflächen und der Rissweite abhängig. Solche Grössen müssen genau erfasst werden, um Rissverzahnungsmodelle validieren zu können. Oftmals sind auch grossmassstäbliche Versuche notwendig, um Resultate zu erhalten, die repräsentativ für reale Tragwerke sind. Solche Grossversuche sind aber sehr aufwendig in der Durchführung und weisen im Allgemeinen ein komplexes Rissmuster auf, wobei die exakten Rissstellen nicht vorausgesagt werden können. Es wurden bereits verschiedene Messsysteme zum Messen von Rissen entwickelt, die aber in Ihrer Anwendbarkeit oftmals stark eingeschränkt sind. Das liegt hauptsächlich daran, dass die Auflösung und Genauigkeiten bezüglich der gemessen Risskinematiken, bestehend aus der Rissweite und –schiebung, meistens nicht ausreichen, um verlässliche Aussagen über das tatsächliche Trag- und Verformungsverhalten des Materials zu treffen. Das genaue Messen von Rissen mit einer hohen Auflösung ist deshalb zentral, stellt aber eine grosse Herausforderung dar.

Wie wurden Risse bis anhin gemessen?
Das bis vor einiger Zeit übliche Verfahren zur Messung von Rissen an Experimenten bestand darin, den Versuch an ausgewählten Last- oder Verformungszuständen zwischenzeitlich zu stoppen und relevante Rissbreiten von Hand durch Risslineale oder mit Risslupen direkt an der Versuchsoberfläche zu messen. Dieses manuelle Messverfahren ist aber anfällig für Messfehler und zudem sehr aufwendig, insbesondere bei Grossversuchen mit einer Vielzahl von Rissen. Ausserdem fehlen bei Elementen mit geringer Verformungskapazität in der Regel relevante Messungen nahe der Versagenslast aufgrund des damit verbundenen Risikos hinsichtlich der Sicherheit für das Personal.
Alternative Messverfahren – wie z.B. die Verwendung von DEMEC, NDI oder LVDTs («linear variable differential transformers») – verbessern die Genauigkeit der Rissmessungen sowie die zeitliche Auflösung, sind jedoch weiterhin beschränkt auf wenige vordefinierte Rissstellen und deshalb auch kaum oder nur schwer anwendbar auf komplexe Rissmuster, bei welchen die genauen Rissstellen in der Regel nicht vorausgesagt werden können.

Welche Vorzüge bietet digitale Bildkorrelation (DIC)?
Unter digitaler Bildkorrelation (bekannt als DIC für «digital image correlation») versteht man ein kamerabasiertes Verformungsmessverfahren von Oberflächen, bei welchem die Verformung eines aus zufälligen Punkten bestehenden Oberflächenmusters durch Korrelationsalgorithmen gemessen wird. Aus den dabei gewonnenen vollflächigen und hochpräzisen Verschiebungsmessung können mit relativ einfachen Verfahren auch Oberflächendehnungen des Bauteils berechnet werden. Gegenüber herkömmlichen Messverfahren liefert DIC quasi-kontinuierlichen Messungen (räumlich und zeitlich), und eröffnet so neue Möglichkeiten zur sehr detaillierten und verlässlichen Erfassung des Rissverhaltens in Laborversuchen.
Zwar wird DIC bereits in vielen Forschungsinstitutionen zur Messung von Rissöffnungen und –schiebungen verwendet, jedoch werden die Resultate meistens nur an wenigen diskreten Stellen mittels manuell gesetzten Extensometern ermittelt, was zu Folge hat, das viele wertvolle Informationen verloren gehen. Solche manuelle Verfahren sind auch kaum anwendbar auf Grossversuche mit komplexen Rissmuster. Die in Grossversuchen erzeugten DIC Datenmengen sind extrem gross und können daher nur durch automatische Verfahren effizient zu brauchbaren Resultaten weiterverarbeitet werden. Zudem müssen die Rissöffnungen und -schiebungen über virtuelle Referenzpunkte, die etwas von den tatsächlichen Rissufern entfernt sind, bestimmt werden, um verzerrungsfreie Messungen zu erhalten. Das führt dazu, dass schon geringfügige Rotationen des Versuchskörpers berücksichtigt werden müssen (insbesondere für Rissschiebungsmessungen), was das Messverfahren um einiges erschwert. Hier muss jedoch erwähnt werden, dass letzterer Punkt für alle Rissmessverfahren gilt, bei denen Rissuferverschiebungen nicht direkt, sondern über Referenzpunkte, die nur schon geringfügig vom Rissufern entfernt liegen, gemessen werden (also auch für Rissmessungen mittels manueller DIC-Extensometer aber auch z.B. bei der Verwendung von DEMEC, NDI oder LVDTs).

Prinzip der Verschiebungsmessung durch DIC. 
DIC-Aufbau im Large Universal Shell Element Tester (LUSET) mit zwei Kameras, um 3D-Verschiebungen zu messen. Bildquelle: Mata Falcón et al. 2020.
Um DIC effizient zur Erfassung des Rissverhaltens in Betonversuchen einsetzen zu können – was durch andere bekannte Messverfahren nicht mit dieser Genauigkeit und Auflösung möglich wäre – wurden in unserer Forschungsgruppe von einigen Jahren erste Schritte in Richtung des heutigen vollautomatischen DIC-basierten Rissmessungs-Tools «ACDM» unternommen.
Was waren die ersten Schritte bei der Entwicklung von ACDM?
Das Grundkonzept von ACDM bestand von Anfang an darin, die Beziehung, dass die lokale Oberflächenzugdehnung an Rissen theoretisch unendlich gross wird, zu nutzen. Aufgrund der endlichen Auflösung des DIC und der Tatsache, dass das Dehnungsfeld oftmals gefiltert wird, um das Messrauschen zu verringern, resultieren an den Rissen jedoch endliche Zugdehnungen. Die Grösse der berechneten Hauptzugdehnung steht nun im Zusammenhang mit der Risskinematik, also mit der Rissöffnung (Verformung senkrecht zur Rissneigung) und der Rissschiebung (Verformung parallel zur Rissneigung). Somit suchten wir nach einem Verfahren, das Risse an Stellen mit hohen Hauptzugdehnungen extrahiert. Eine erste Lösung bestand darin, Zonen mit hohen Dehnungen zu bestimmen und diese dann durch bewährte morphologische Operationen in Risslinien (als Rissskelett) zu verdünnen.
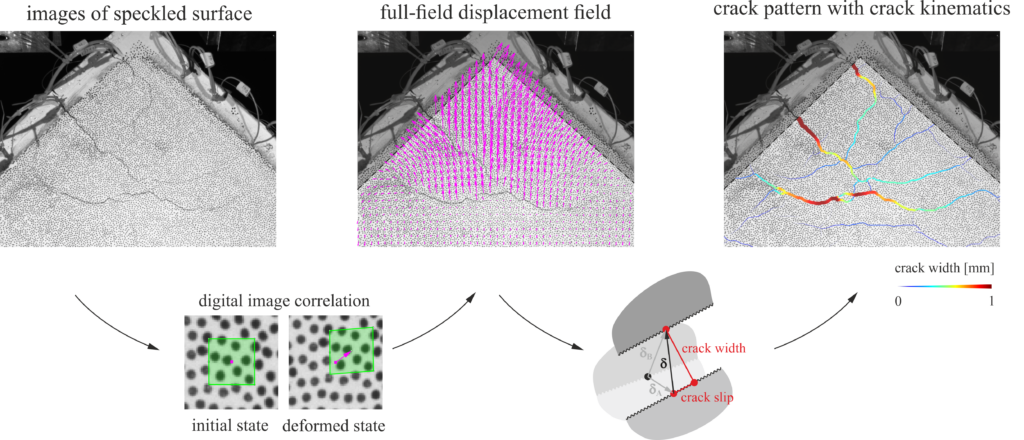
Die erkannten Risslinien haben gegenüber einzelnen unabhängigen Risspunkten den grossen Vorteil, dass für jeden Risspunkt die lokale Rissneigung berechnet werden kann, die unter anderem für die Bestimmung der Risskinematiken benötigt wird. Die Rissuferverschiebungen wurden in einem ersten Schritt mittels zweier Referenzpunkte (pro Rissufer) berechnet, damit – wie bereits erwähnt – lokale Rotationen des Versuchskörpers berücksichtigt werden konnten.
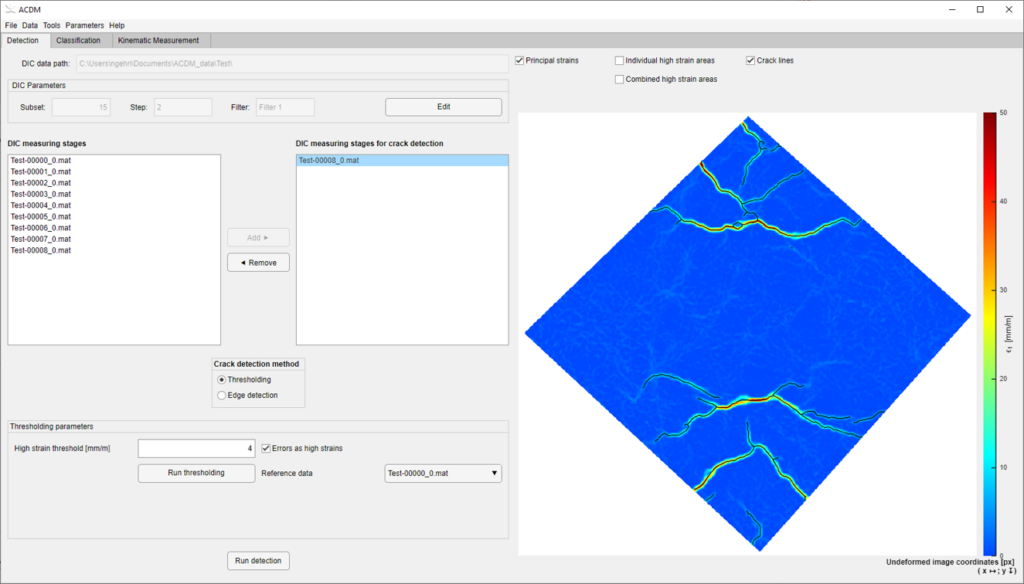
Wie wurde ACDM zur vollautomatischen Software weiterentwickelt?
Die Methoden wurden von Anfang in eine Benutzeroberfläche integriert, um die Anwendung des Tools zu erleichtern. Bei Versuchen mit einem verhältnismässig einfachen Rissmuster zeigte sich schnell, dass ACDM sehr genaue Resultate zu den Rissorten und den Risskinematiken liefern konnte. Bei komplexeren Rissmuster zeigten sich aber Probleme mit verzerrten Resultaten in Bereichen nahe von Rissverzweigungen, bei welchen das Verfahren versagte. Deshalb wurde in einem nächsten Schritt das Verfahren zur Risserkennung überarbeitet. Anstelle von Zonen mit hohen Dehnungen, die zu Risslinien verdünnt werden, werden in der heutigen Version von ACDM die Risslinien direkt als Kanten im Dehnungsfeld extrahiert. Zudem wurde bei der Berechnung der Risskinematiken die Anzahl von Referenzpunkten erhöht und ein Algorithmus entwickelt, der die Verlässlichkeit der Resultate verbessert.
ACDM steht der Öffentlichkeit unter https://gitlab.ethz.ch/ibk-kfm-public/acdm als Open-Source-Software zur Verfügung. In diversen Experimenten unserer Forschungsgruppe und insbesondere bei unseren Grossversuchen im Large Universal Shell Element Tester (LUSET) wurde ACDM bereits erfolgreich angewendet und konnte so zu relevanten neuen Erkenntnissen zum Tragverhalten von Beton beitragen. Beispielsweise haben Alexander Beck und Demis Karagiannis im Rahmen ihrer kürzlich veröffentlichten Doktorarbeiten 2.0 x 2.0 grosse Scheiben in LUSET getestet, wobei ACDM in der Auswertung der Versuchsresultaten verwendet wurde. Die damit gewonnenen Informationen zum Rissverhalten hatten eine zentrale Bedeutung bei der Entwicklung und Validierung ihrer mechanischen Modelle. Aber auch ausserhalb der ETH fand ACDM anklang und wurde schon in diversen Studien zur Auswertung von Experimenten genutzt.

Rissbild eines Scheibenversuchs in LUSET unter kombinierter Schub- und Biegebeanspruchung. Bildquelle: Karagiannis 2021. 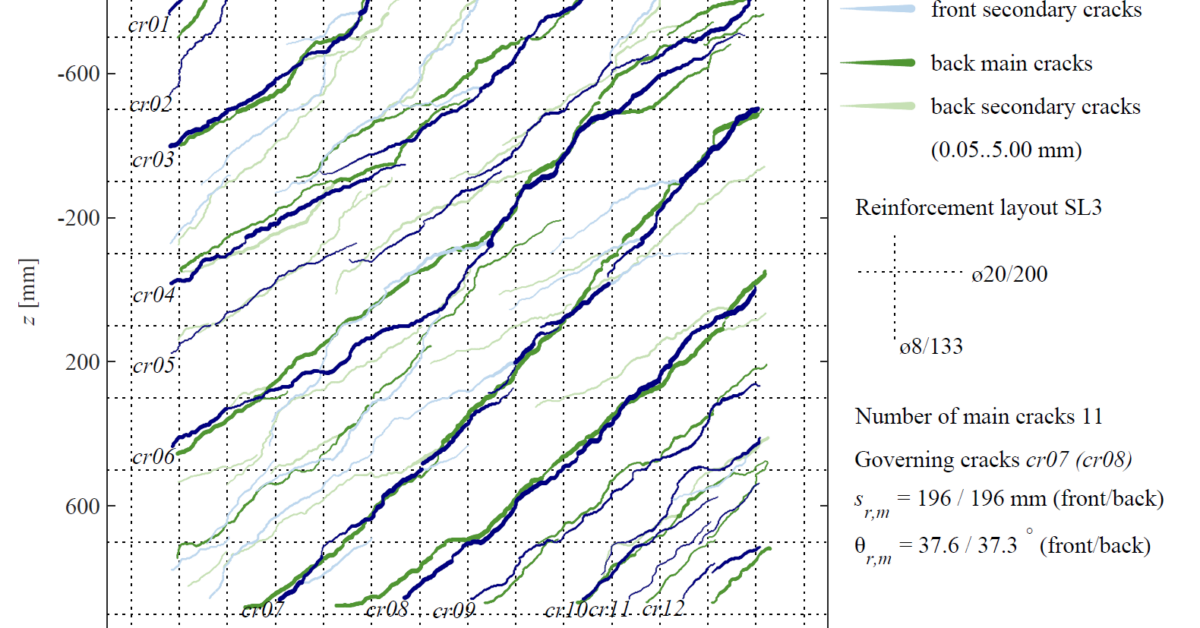
Rissbild eines Schubversuchs in LUSET. Bildquelle: Beck 2021.
Damit das auch in Zukunft weiterhin so bleibt, sind wir daran, ACDM laufend zu verbessern. Ein Ziel, das wir zum Beispiel seit längerem verfolgen, ist die Echtzeitmessung von Rissen mittels ACDM, was uns ermöglichen würde, Versuche unter Steuerung von Rissweiten oder Rissschiebungen (was beispielsweise in Versuchen mit faserverstärkten Betonelementen wichtig ist) zu belasten. Weiteres Potential von ACDM sehen wir auch in der Überwachung bestehender Tragwerke zur Früherkennung von Schäden. Entsprechende Untersuchungen sind Gegenstand aktueller Forschung.
Nicola Gehri
Link to English version: Shear behaviour of lightly reinforced concrete membrane elements
Bei der Beurteilung der Tragsicherheit von bestehenden Tragwerken zeigt sich immer wieder, dass die momentan zur Verfügung stehenden Berechnungsmethoden unzureichend sind, insbesondere betreffend Schubtragfähigkeit. Das liegt daran, dass zur Analyse bestehender Tragwerke in der Regel die gleichen Modelle angewendet werden, die auch für die Bemessung neuer Tragwerke gelten, dass die Querkraftbewehrungsgehalte in alten Bauwerken aber auf Grund der früher geltenden Normbestimmungen oft sehr niedrig sind. In meiner Dissertation, die ich kürzlich erfolgreich verteidigt habe, versuchte ich das Verständnis des Lastverformungsverhaltens von Stahlbeton-Scheibenelementen mit sehr geringen Bewehrungsgehalten im ebenen Spannungszustand zu verbessern.
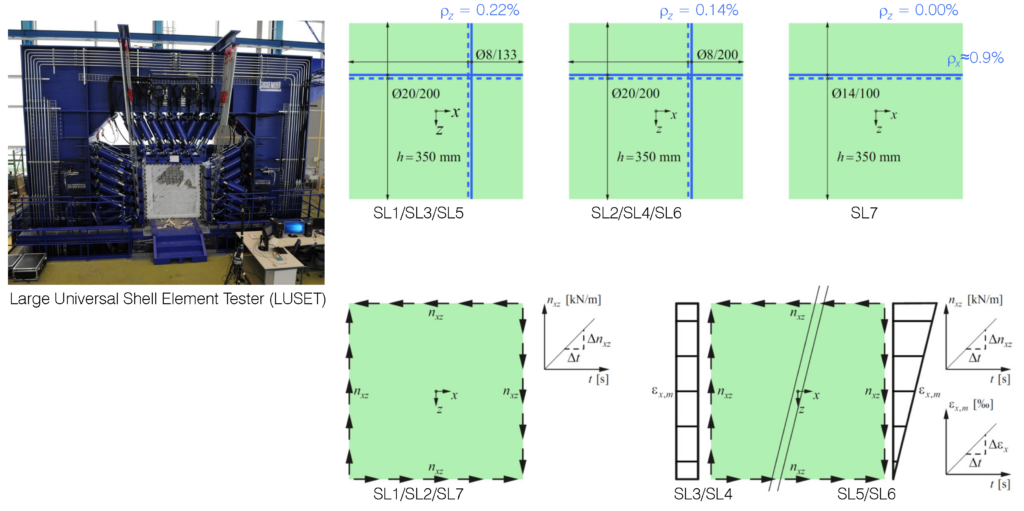
Dazu wurde eine Serie von Schubversuchen an sechs grossformatigen Scheibenelementen mit sehr geringen vertikalen Bewehrungsgehalten von ρz=0.14…0.22%, sowie an einem uniaxial bewehrten Scheibenelement durchgeführt. Drei Elemente wurden unter einer reinen Schubbeanspruchung in der Ebene und vier Elemente unter einer Schubbeanspruchung in der Ebene mit aufgebrachter Längsdehnung mit und ohne Gradient über die Höhe der Versuchskörper getestet. Die Versuche wurden in der neu entwickelten Versuchsanlage Large Universal Shell Element Tester (LUSET) durchgeführt. Dabei kamen moderne Messtechniken zum Einsatz, wobei insbesondere die digitale Bildkorrelation zur Erfassung der Verformungen und Rissbilder auf der Betonoberfläche sowie die faseroptischen Dehnungsmessungen entlang der einbetonierten Bewehrungsstäbe wertvolle und umfassende Daten zur Charakterisierung des Verformungsverhaltens lieferte.
Die Versuchsergebnisse wurden hinsichtlich des Lastverformungsverhaltens der Scheibenelemente, aber auch hinsichtlich ihres Rissverhaltens und der Rissverzahnung (aggregate interlock), d.h. des durch die Unebenheit der Risse entstehenden Verzahnungswiderstandes, mit theoretischen Modellen verglichen. Die Modellvorhersagen bzgl. der Traglast wie auch des Verformungsvermögens des ursprünglich von Prof. Dr. Walter Kaufmann entwickelten gerissenen Scheibenmodells mit fester Rissrichtung (CMM-F) waren hervorragend, insbesondere unter Verwendung des rough crack model (RCM) als Rissverzahnungsmodell. Das RCM ist ein rein empirisches Rissverzahnungsmodell, das mit einer Vielzahl von Versuchen kalibriert wurde. Das CMM-F unter Verwendung des two-phase model (TPM) von Walraven, das ebenfalls empirisch kalibriert wurde, aber auf einem mechanischen Modell basiert und deshalb wohl das am weitesten verbreitete Rissverzahnungsmodell ist, führte zu konservativen Vorhersagen. Dies ist im Hinblick auf die Anwendung von Querkraftmodellen auf Basis des TPM in der Bemessungspraxis positiv zu bewerten (z.B. die Querkraftbestimmungen für Bauteile ohne Schubbewehrung in der SIA 262). Ein weiteres wichtiges Ergebnis der Versuchsserie hinsichtlich der Bemessungspraxis war die Bestätigung der bewährten Empfehlung, bei normalfesten Betonen einen Mindestbewehrungsgehalt von ρz =0,2% vorzusehen. Zu dieser Erkenntnis hat insbesondere geführt, dass die Versuchskörper mit ρz=0.14% eine Bruchlast aufwiesen, die nicht oder nur unwesentlich höher war als die Risslast, während die Last bei den Versuchskörpern mit ρz=0.22% nach dem Reissen noch gesteigert werden konnte. Es wird deshalb davon abgeraten, diesen Wert zu senken, wie dies z.B. gemäss fib MC 2010 oder in der SIA 262 zugelassen ist.
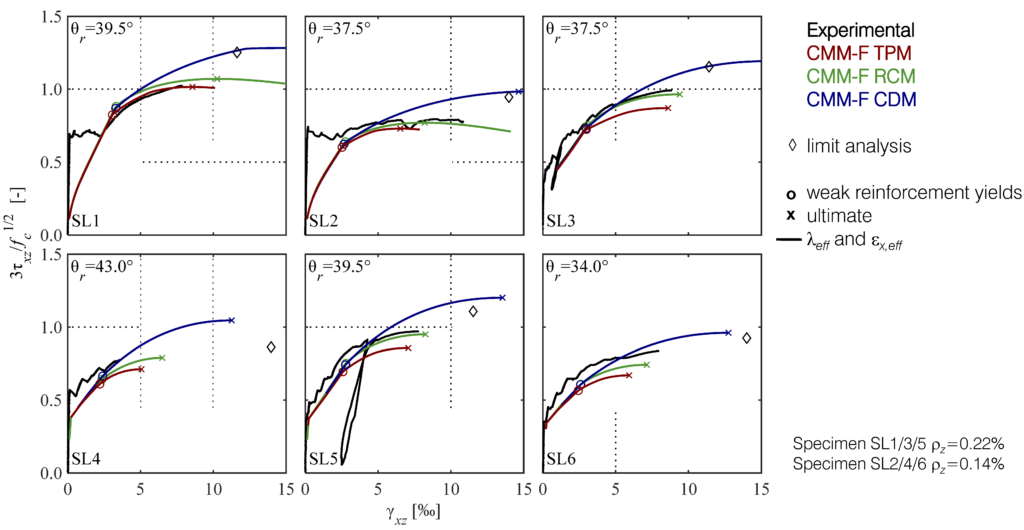
In den Versuchen konnte auch gezeigt werden, dass die verfügbaren Rissverzahnungsmodelle aus der Literatur nur mässig gut funktionieren, wenn es darum geht, die Rissverzahnungsspannungen aus der gemessenen Risskinematik zu bestimmen. Dies war ein Ziel meiner Forschung, um diese Spannungen in Zukunft vielleicht vorhersagen zu können. Die Ergebnisse dieser Berechnungen variierten aber sehr stark. Somit sind die Rissverzahnungsmodelle nicht geeignet, den Spannungszustand eines beliebig geformten Risses in einem Bauteil vorherzusagen. Zudem sind Rissabstände, -neigungen und -formen aufgrund vieler lokaler Einflüsse wie Eigenspannungszuständen, der Variation der Zugfestigkeit innerhalb des Versuchskörpers, unterhalb der Betondeckung verlaufenden Bewehrungsstäben und der Verteilung der Zuschlagstoffe im Beton kaum vorhersagbar.
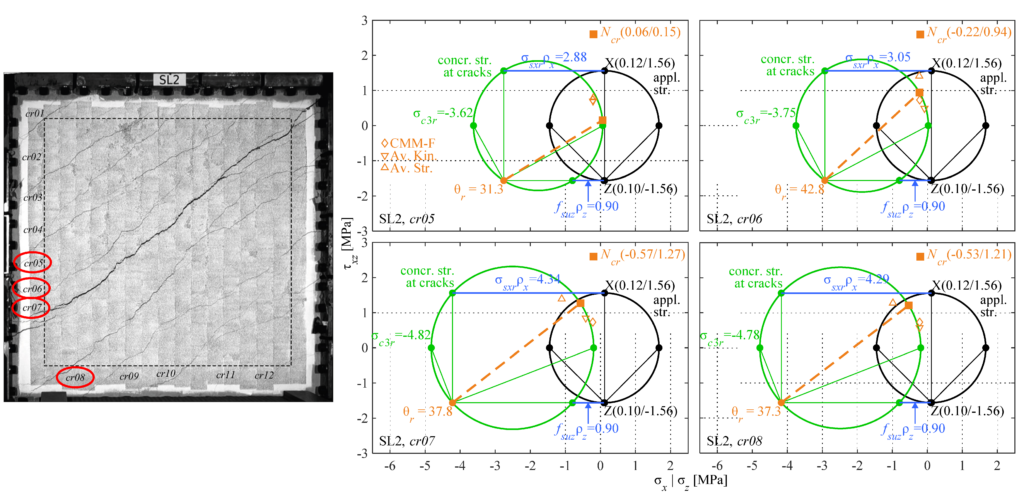
Alexander Beck
Link to English version: Eco-friendly concrete structures?
Beton – Grundlage unserer Zivilisation
Beton war für die Industrialisierung und die Entwicklung unserer urbanen Zivilisation unabdingbar und ist heute der mit Abstand am meisten verwendete Baustoff: Jährlich werden rund 15…20 Milliarden Kubikmeter Beton verbaut, also gut zwei Kubikmeter pro Erdbewohner weltweit(1). Die Betonbauweise ist derart weit verbreitet, weil sie gute mechanische Eigenschaften(2) mit hoher Dauerhaftigkeit(3) und Feuerwiderstand vereint, bei weltweiter Verfügbarkeit zu tiefen Kosten. Die beiden letztgenannten Vorteile werden oft übersehen, sind aber wohl die wichtigsten Faktoren für die grosse Verbreitung der Betonbauweise.
(1) Genaue Zahlen sind nicht verfügbar; die Schätzung basiert auf der von Cembureau registrierten jährlichen weltweiten Produktion von 3.99 Milliarden Tonnen Zement (Kennzahlen Cembureau) hochgerechnet analog zum Vorgehen der Cement Sustainability Initiative unter Annahme von 300 kg Zement mit 70% Klinkeranteil pro Kubikmeter Beton. In der Schweiz werden gemäss Statistik des FSKB jährlich 15 Millionen Kubikmeter Transportbeton geliefert, was bei einem Transportbetonanteil von 75% einem jährlichen Betonverbrauch von rund 2.5 Kubikmeter pro Kopf entspricht.
(2) Beton weist eine hohe Druckfestigkeit auf, versagt aber bereits unter geringer Zugbeanspruchung spröd. Die Erfindung des Stahlbetons, in welchem eine Bewehrung – in der Regel Betonstahl – die Zugkräfte aufnimmt, war daher für den Erfolg der Betonbauweise essentiell. Andererseits sorgt der Beton dafür, dass sich die Bewehrung bei einem Brandereignis nur langsam erwärmt und sorgt damit für einen hohen Feuerwiderstand. Betonstahl – in der Schweiz werden jährlich rund 1.6 Millionen Tonnen verbaut – wird heute praktisch ausschliesslich aus Altmetall hergestellt.
(3) Dank der hydraulischen Eigenschaften des Bindemittels Zement ist Beton selbst unter Wasser dauerhaft. Die Lebensdauer bewitterten unbewehrten Betons ist daher nahezu unbegrenzt, wie beispielsweise das Pantheon in Rom beweist. Dies gilt auch für Stahlbeton, solange die Bewehrung nicht korrodiert. Letzteres hängt primär von der Exposition ab: Während in trockenen Innenräumen keine Korrosion auftritt, müssen Bauwerke, die Feuchtigkeit und Chloriden ausgesetzt sind, unter Umständen nach einigen Jahrzehnten instandgesetzt werden. Im Vergleich mit den meisten anderen Baustoffen ist die Dauerhaftigkeit von Stahlbeton jedoch auch unter solcher Exposition sehr hoch.
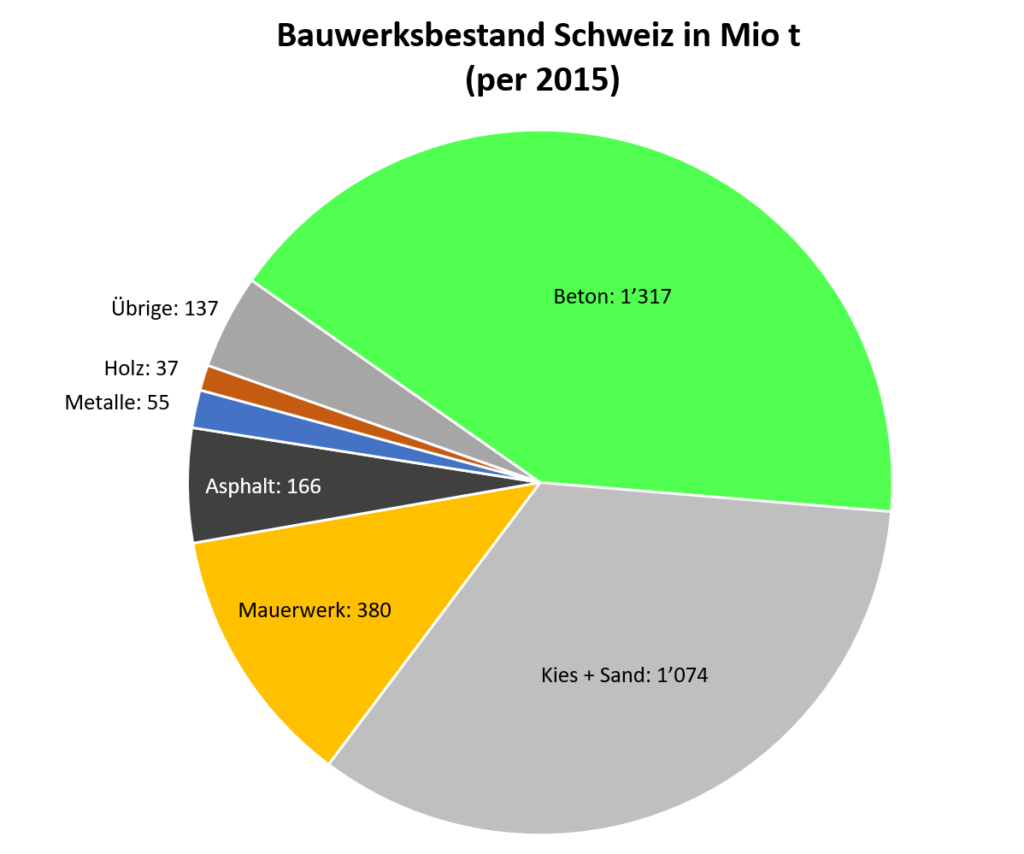
Hoher Ressourcenverbrauch und Treibhausgasemissionen
Offensichtlich geht mit der grossen Verbreitung der Betonbauweise ein hoher Ressourcenverbrauch einher, auch wenn dieser durch die Wiederverwendung von Betonabbruch als rezyklierte Gesteinskörnung für neuen Beton reduziert werden kann. Zudem trägt der als Bindemittel im Beton verwendete Zement je nach Berechnungsweise rund 5…8% zu den weltweiten Treibhausemissionen bei(4). Vor dem Hintergrund des Klimawandels ist es daher naheliegend, einen Ersatz von Beton durch andere Baustoffe, insbesondere Holz, zu fordern.
(4) Bei der Herstellung von Portlandzement (auch als Klinker bezeichnet) durch die Kalzinierung von Kalkstein und Mergel werden rund 470 kg CO2 pro Tonne freigesetzt. Die Erhitzung der Ausgangsstoffe auf die zur Kalzinierung notwendigen Temperatur von ca. 1450°C verursacht weitere 100…500 kg CO2 pro Tonne Klinker (je nach verwendetem Brennstoff). Durch den hohen Zementverbrauch von jährlich 3.99 Milliarden Tonnen (Kennzahlen Cembureau) – allein in der Schweiz 4.21 Millionen Tonnen (Kennzahlen cemsuisse) resultieren entsprechend hohe Treibhausgasemissionen.
Ersatz von Beton: Taugliche Lösung?
Der Ersatz von Beton ist jedoch nur teilweise möglich und zumindest für sich alleine nicht zielführend. Einerseits ist Beton für viele Anwendungen faktisch alternativlos: Untergeschosse von Gebäuden, Stützmauern, Talsperren oder Tunnels in anderer Materialisierung sind hinsichtlich Tragwiderstand, Dauerhaftigkeit und Kosten nicht annähernd gleichwertig. Andererseits können alternative Baustoffe nur einen kleinen Teil der weltweit benötigten Mengen an Baustoffen abdecken(5), und sie verursachen bei grosser Verbreitung entsprechend hohe Treibhausgasemissionen, die in den meisten Fällen sogar höher sind als diejenigen von Beton(6).
(5) Beispielsweise beträgt der jährliche Rundholzeinschlag weltweit heute rund 2 Milliarden Kubikmeter, wovon etwa 500 Millionen zu Holzprodukten verarbeitet werden (FAO Global Forest Products Facts and Figures 2018). Dies entspricht wenigen Prozenten des Betonverbrauchs. Selbst bei einer starken Erhöhung dieser Menge (soweit dies mit nachhaltiger Forstwirtschaft machbar ist) könnte nur ein kleiner Teil des Betons substituiert werden.
(6) Hier ist zwar Massivholz eine Ausnahme, aber viele Holzwerkstoffe verursachen ebenfalls hohe Emissionen. Beispielsweise emittiert Sperrholz pro Kubikmeter rund sechsmal mehr CO2 als Beton (KBOB Ökobilanzdaten im Baubereich).

© dsp Ingenieure + Planer AG
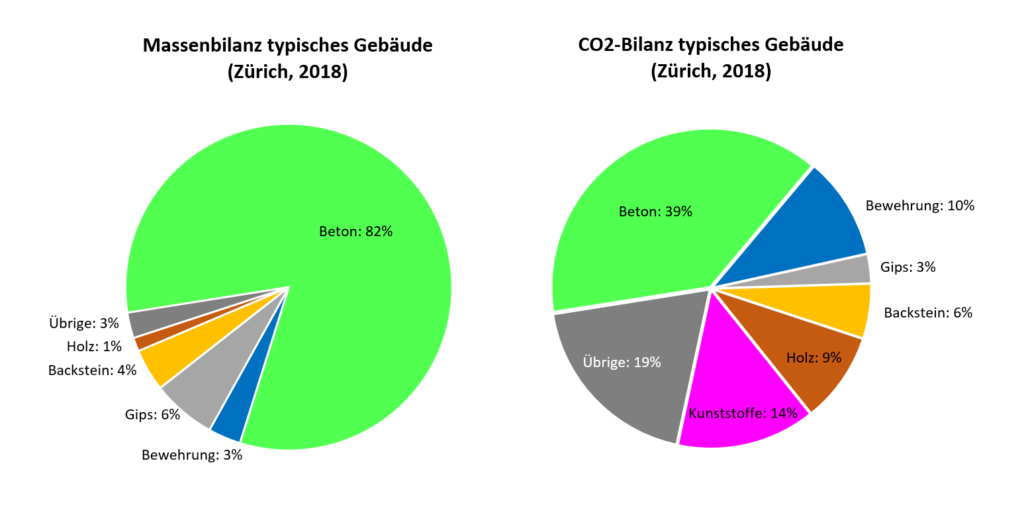
Wenn der Ressourcenverbrauch und die Treibhausgasemissionen der Baubranche substantiell reduziert werden sollen, kann daher nicht einfach Beton ersetzt werden. Wenn schon müsste die Bautätigkeit insgesamt eingeschränkt werden, verbunden mit einem Übergang zur Kreislaufwirtschaft. Solche Überlegungen haben in industrialisierten Ländern ihre Berechtigung: Wir haben bereits eine gute Infrastruktur und wir können uns höhere Kosten für ihren Erhalt, Ersatz oder Ausbau unter Verwendung alternativer Baustoffe – gegebenenfalls in Form von Lenkungsabgaben zu deren Förderung – leisten. In Entwicklungs- und Schwellenländern ist dies jedoch kaum realistisch, und ich halte es für anmassend, wenn industrialisierte Länder von diesen Ländern die Berücksichtigung solcher Kriterien beim Aufbau ihrer Infrastruktur fordern, oder sogar einen Verzicht verlangen. Hält man sich vor Augen, dass diese Länder heute rund 85% des Zements verbrauchen (https://www.suedwind-magazin.at/zweischneidiges-schwert), ist der Ersatz von Beton kaum die Lösung.
Umweltfreundlichkeit durch effiziente Tragwerke
Vielmehr gilt es, den Ressourcenverbrauch und die Emissionen der Betonbauweise zu reduzieren. Das Cembureau hat dazu den «5C»-Ansatz entwickelt, mit dem folgende fünf Punkte verfolgt werden:
- Clinker – Reduktion fossiler Brennstoffe bei der Klinkerherstellung
- Cement – Reduktion des Klinkergehalts im Zement
- Concrete – Reduktion des Zementgehalts im Beton
- Construction – Reduktion des Betonverbrauchs im Bauwerk
- Carbonation – Erhöhung der Karbonatisierung
Der erste Punkt ist in der Schweiz bereits weitgehend umgesetzt: Die Schweizer Zementindustrie bezieht heute über zwei Drittel der Energie aus alternativen Brennstoffen. Auch der Klinkergehalt im Schweizer Zement wurde bereits stark reduziert: Der Anteil des bis 1998 praktisch ausschliesslich eingesetzten reinen Portlandzements beträgt heute weniger als 7% (Kennzahlen cemsuisse). Eine weitere Reduktion des Klinkergehalts im Zement ist möglich, wobei jedoch die Dauerhaftigkeit nicht beeinträchtigt werden darf. Aus demselben Grund ist eine Reduktion des Zementgehalts im Beton nicht ohne weiteres möglich(7).
(7) Dauerhaftigkeitsprobleme treten im Betonbau primär durch Korrosion der Bewehrung auf. Die Alkalität des Betons, welche durch die Verwendung von Klinker gewährleistet wird, schützt die Bewehrung vor Korrosion. Dies ist bei einer Reduktion von Zementgehalt und Klinkeranteil im Zement bei exponierten Betonbauteilen zu beachten.
Betonbauten absorbieren durch die Karbonatisierung des Betons (CO2-Aufnahme) über ihre Lebensdauer 10-20% (je nach Berechnungsmethode) der emittierten Treibhausgase. Dieser Anteil kann beispielsweise durch die gezielte Karbonatisierung von Betonabbruchgranulat erhöht werden (https://www.aramis.admin.ch/Texte/?ProjectID=47360). Eine interessante Alternative besteht darin, CO2 an der Emissionsquelle einzufangen und daraus Kalkstein herzustellen, wie dies beispielsweise die Firma Blue Planet bereits macht. Wird dieser synthetische Kalkstein als Gesteinskörnung für Beton eingesetzt, würden Betonbauten in Zukunft mehr CO2 absorbieren, als bei der Zementherstellung emittiert wird. Ob sich der Prozess allerdings skalieren und wirtschaftlich betreiben lässt, ist gegenwärtig noch nicht absehbar.
Das grösste Potential sehe ich persönlich in der Reduktion des Betonverbrauchs im Bauwerk, die sich am besten mit statisch effizienten Tragwerken erreichen lässt. Solche Tragwerke zeichnen sich ja eben gerade dadurch aus, dass sie die Lasten mit geringem Eigengewicht (und somit kleinem Ressourcenverbrauch und Emissionen) materialgerecht abtragen. Hier können und müssen die im konstruktiven Ingenieurbau tätigen Bauingenieurinnen und Bauingenieure ihren Beitrag zum Klimaschutz leisten.
Aufgrund niedriger Materialpreise bei steigenden Lohnkosten wurde die statische Effizienz als Entwurfsziel in den letzten Jahrzehnten leider allzu oft vernachlässigt. Stattdessen wurden einfache und schnell zu erstellende Bauwerke favorisiert, auch wenn diese wesentlich mehr Material erforderten. Zudem wurden die Mindestabmessungen von Betonbauten laufend erhöht: Im Hochbau um die Schalldämmung zu gewährleisten und Haustechnikleitungen einlegen zu können(8), im Tiefbau um eine maximale Dauerhaftigkeit zu gewährleisten(9). Hier bietet der zunehmende Druck, Ressourcenverbrauch und Treibhausgasemissionen zu reduzieren, den Bauingenieurinnen und Bauingenieuren die Chance, sich auf eine ihrer ureigenen Kompetenzen zu besinnen und der statischen Effizienz wieder den Stellenwert einzuräumen, den sie verdient.
(8) Ein Beispiel hierfür sind Häuser mit kontrollierter Lüftung, wie dies zur Erreichung des «Minergie»-Labels notwendig ist. Um die Lüftung in die Decken integrieren zu können, beträgt die Deckenstärke meistens 26 cm, obschon statisch eine viel dünnere Decke ausreichend wäre.
(9) Die Anforderungen an die Dauerhaftigkeit wurden aufgrund der Erfahrung mit Korrosionsschäden an frühen Betonbauten stark erhöht, was zweifellos gerechtfertigt ist: Ein frühzeitiger Ersatz eines korrodierten Bauwerks ist gewiss nicht nachhaltig. Die heute von vielen Normen und Bauherren pauschal an alle Bauwerke gestellten Maximalanforderungen hinsichtlich Dauerhaftigkeit sollten jedoch hinterfragt und differenziert werden, da sie zu Lasten von Ressourcenverbrauch und Treibhausgasemissionen gehen.
Statisch effiziente Betonbauten
Die effizientesten Betonbauten sind zweifellos Bogen- und Schalentragwerke, welche die Lasten bei geringem Eigengewicht primär über Druckkräfte abtragen. Allerdings gilt dies nur für den Endzustand. Die konventionelle Erstellung solcher Tragwerke erfordert hingegen oft sehr aufwändige Lehrgerüste und Schalungen, wodurch ihre Vorteile stark relativiert werden.

Hier gilt es, noch effizientere Bauverfahren zu entwickeln, was beispielsweise Gegenstand aktueller Forschung im NCCR dfab an der ETH Zürich ist (https://dfab.ch/streams/lightweight-flexible-formwork). Solche Bestrebungen sind keineswegs neu: Beispielsweise entwickelte J. Melan bereits 1892 ein System zur Erstellung von Bögen, bei dem ein leichter Stahlbogen zugleich als Lehrgerüst für den Beton und dessen Hauptbewehrung dient. Mit der auf dem gleichen Prinzip basierenden «CSFT» (Concrete Filled Steel Tube) Bauweise werden in China heute Bogenbrücken mit über 500m Spannweite erstellt (https://concrete.ethz.ch/brd/arch-bridges/).
Bögen und Schalen eigenen sich naturgemäss nicht für alle Anwendungen, beispielsweise Geschossdecken, die meistverbreitete Anwendung von Stahlbeton. Auch geometrisch einfachere Bauwerke können jedoch statisch effizient sein, wenn sie entsprechend konzipiert werden. Hier gilt es einige Grundprinzipien zu beachten, die für Bauingenieurinnen und Bauingenieure selbstverständlich sein sollten:
- Effiziente statische Systeme wählen: Durchlaufträger sind wesentlich effizienter als einfache Balken
- Effiziente Querschnitte wählen: Profilierte Träger haben bei gleichem Gewicht wesentlich höhere Steifigkeit und Widerstand als Rechteckquerschnitte
- Trägerhöhe der Beanspruchung anpassen
- Bauvorgang im Entwurf berücksichtigen
Für Geschossdecken eignen sich insbesondere Rippen-, Kassetten- und Hohlkörperdecken, mit denen sich gegenüber einer Vollplatte in vielen Fällen mehr als 50% des Materials einsparen lassen. Auch hier gibt es bestehende Systeme, beispielsweise standardisierte Schalungen für Ortbeton-Kassettendecken und vorfabrizierte Hohlkörperdecken. Neue Möglichkeiten sind Gegenstand aktueller Forschung im NCCR dfab an der ETH Zürich.
Zusammenfassung
Die Reduktion von Ressourcenverbrauch und Treibhausgasen ist angesichts des Klimawandels ein Gebot der Stunde. Der Ersatz von Beton durch andere Baustoffe ist jedoch nur in wenigen Fällen zielführend, da nicht der Beton an sich das Problem ist, sondern seine grosse Verbreitung: Wenn andere Baustoffe in solch grossen Mengen verbaut werden, verursachen sie einen ebenso grossen Ressourcenverbrauch und ähnlich grosse Treibhausgasemissionen wie Beton.
Vielmehr müssen unsere Bauwerke insgesant umweltfreundlicher werden. Mit statisch effizienten Tragwerken können und müssen projektierende Bauingenieurinnen und Bauingenieure hier einen substantiellen Beitrag zum Klimaschutz leisten. Damit solche Tragwerke auch wirtschaftlich sind, muss der Bauvorgang im Tragwerksentwurf einbezogen werden. Zudem müssen wir Bauverfahren entwickeln, mit denen komplexere Bauwerke effizient hergestellt werden können.
An unserer Professur versuchen wir, mit der Vermittlung der Grundlagen für einen effizienten Tragwerksentwurf und mit unserer Forschung im Bereich neuer, digitaler Fabrikationsverfahren unseren Beitrag zu leisten.
Walter Kaufmann
Link to English version: Learning to learn: Digital learning applications for structural concrete
So wie das grundsätzliche Prinzip der Betonherstellung sich in den letzten hundert Jahren nur geringfügig geändert hat, so scheint die Lehre im Stahlbetonbau seit jeher gleich geblieben zu sein. Der Unterrichtsstoff basiert auf einer konsequenten Anwendung des Gleichgewichts und einem starken Fokus auf mechanisch konsistente Modelle, deren Tradition an der ETH insbesondere durch Prof. Thürlimann und Prof. Marti geprägt wurde. Dies stärkt nicht nur die Kompetenz im Stahlbetonbau, sondern bildet allgemein ein gutes Fundament für die Ausbildung junger Bauingenieur*innen. Die Auszeichnung von Prof. Kaufmann mit der Goldenen Eule für besondere Leistungen in der Lehre, welche vom Verband der Studierenden der ETH vergeben wird, zeigt zudem auf, dass der Unterricht als kompetent und authentisch wahrgenommen wird. Obwohl wir vom Inhalt unserer Vorlesungen überzeugt sind, sehen wir immer noch Verbesserungspotential – vor allem bezüglich der Unterrichtsmethoden und der dabei verwendeten Hilfsmittel.
Digitalisierung in der Lehre
Der Beton hat im Laufe der Zeit einige Anpassungen in seiner Rezeptur erfahren und auch unsere Vorlesungen wurden zeitgemäss angepasst. Statt einer handgeschriebenen Autographie sind die Folien nun digital. Anstatt ausschliesslich an der Wandtafel zu arbeiten, werden die Notizen nun teilweise auf dem iPad verfasst und projiziert. Ist diese milde Digitalisierung aber tatsächlich eine Innovation in der Lehre? Die klassische Art des Frontalunterrichts scheint alternativlos bei der Wissensvermittlung. Die Fülle an Informationen während einer Vorlesung ist jedoch immens und nicht immer schaffen es die Studierenden, alles aufzunehmen und direkt zu verarbeiten. Oft findet die richtige Auseinandersetzung mit dem Unterrichtsstoff erst später statt: beim Lösen der Kolloquien und Hausübungen oder erst kurz vor der Prüfung, deren Vorbereitung davon geprägt ist, «Kochrezepte» für gewisse Aufgabentypen zu verinnerlichen. Dabei bleibt das Verständnis der Materie leider oft auf der Strecke. Selbstverständlich sehen wir uns als Lehrende hier in der Verantwortung. Wie können wir also die Lehre verbessern, um den Studierenden einen einfacheren Zugang zur eher trockenen Theorie zu ermöglichen?

Innovedum – «Advancing education at ETH»
Unter der Marke “Innovedum” fördert Rektorin Prof. Springman «Initiativen, welche die Lehre an der ETH qualitativ und langfristig weiter entwickeln». Daraus sind bereits zahlreiche innovative Lehr- und Lernprojekte in verschiedenen Disziplinen und mit unterschiedlichen Ansätzen entstanden, beispielsweise Hands on-Workshops oder Gamification der Lehrinhalte.
So fragten auch wir uns, wie neue Lehrelemente eingeführt werden könnten, um das kritische Denken und die Selbstinitiative der Studierenden zu fördern. In der Stahlbeton-Vorlesung befassen wir uns vorwiegend mit der Statik von Tragwerken, welche mittels Grenzzuständen (beispielsweise bezüglich der Tragsicherheit) beschrieben werden. Zwar können diese sauber und mechanisch konsistent hergeleitet werden, sie sind jedoch begrenzt auf isolierte Zustände mit vordefinierten Parametern und vermögen nur bedingt das nicht-lineare Verhalten des Stahlbetons adäquat darzustellen. Das neue Lernmaterial sollte sowohl eine dynamische Darstellung der Resultate wie auch die Möglichkeit zur aktiven Veränderung von Parametern bieten. Aus dieser Idee entstand im Rahmen eines vom Innovedum-Fonds finanzierten Lehrprojekts die Entwicklung von digitalen Lernapplikationen für die Stahlbeton-Vorlesung.
Virtuelle Experimente und Tragwerksanalyse
Der Grossteil der Applikationen besteht aus virtuellen Experimenten, in denen Bauteile und Tragwerke unter verschiedenen Beanspruchungsarten untersucht werden können. Dabei gibt es Beispiele, wo der momentane Spannungszustand bei gegebener Belastung betrachtet wird, aber auch Anwendungen, wo das Last-Verformungsverhalten unter steigender Last verfolgt werden kann. Zentral war für uns, dass die Studierenden die Eingabeparameter möglichst frei verändern können. Die kontinuierliche Verfolgung der Ausgabeparameter sorgt dabei für ein besseres Verständnis der Übergänge zwischen den analytisch behandelten Grenzzuständen. Ein gutes Beispiel dafür ist die Interaktion von Biegung und Normalkraft in Stahlbetonstützen. In der Vorlesung lernen wir, wie wir mithilfe des Dehnungszustands und der Stoffgesetze den Spannungszustand im Stahlbetonquerschnitt bestimmen können. Schon mit wenigen charakteristischen Paaren von Biegung und Normalkraft lässt sich somit eine linearisierte Hüllkurve für die Traglast im M–N-Diagramm konstruieren. Die Änderung der Spannungs- und Dehnungszustände zwischen diesen charakteristischen Punkten erscheint aufgrund der nicht-linearen Beziehungen relativ komplex. Dabei handelt es sich rein geometrisch nur um eine Rotation der Dehnungsebene, was sich wunderbar in einer dynamischen Abbildung darstellen lässt. Durch die Änderung der wirkenden Normalkraft mittels eines Schiebereglers kann man im eigenen Tempo die sich ändernden Dehnungen und Spannungen beobachten (siehe Animation unten). Beispielsweise lässt sich so einfach erkennen, dass im Punkt des maximalen Biegemoments die massgebende Dehnung mit steigender Drucknormalkraft nicht mehr im Bewehrungsstahl sondern im Beton auftritt.
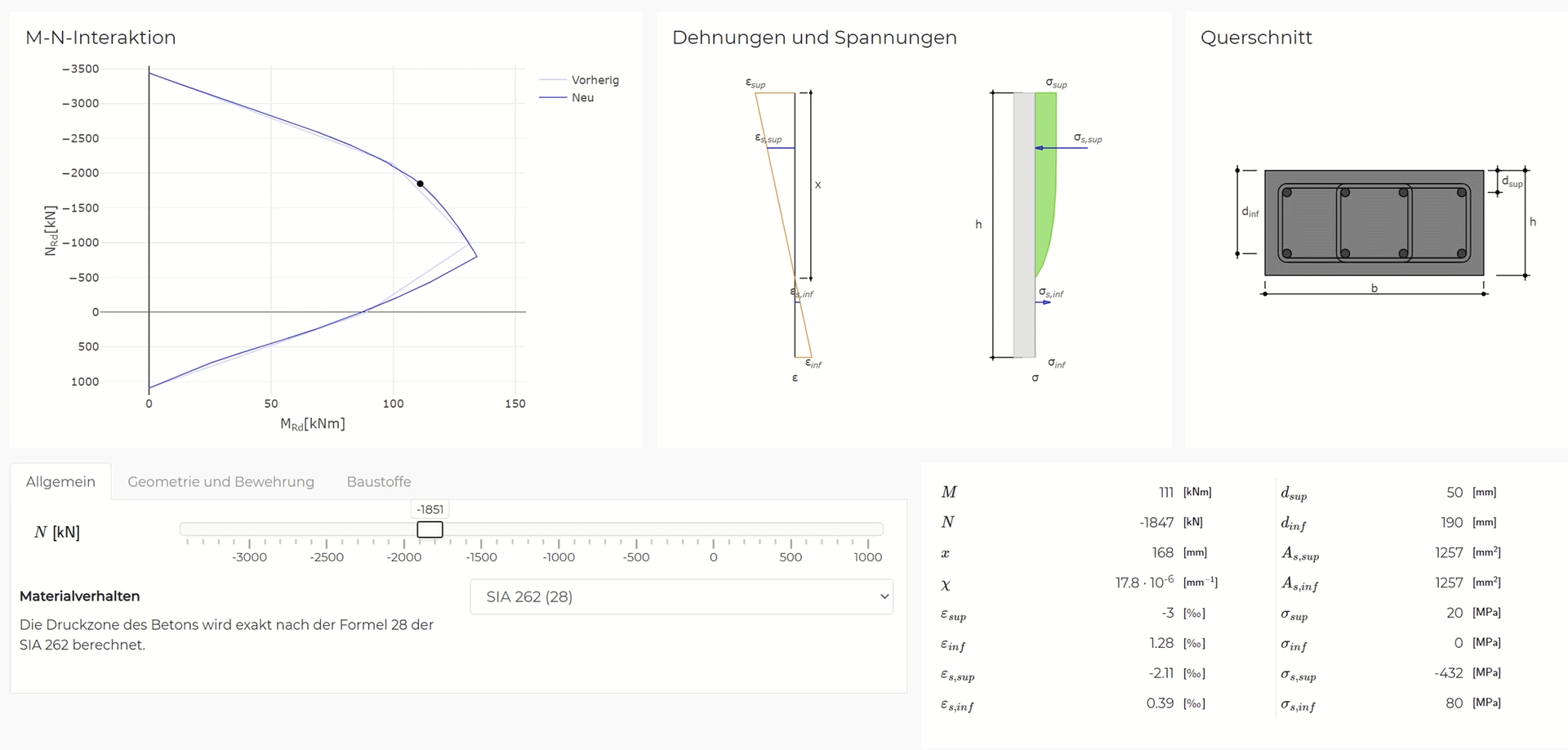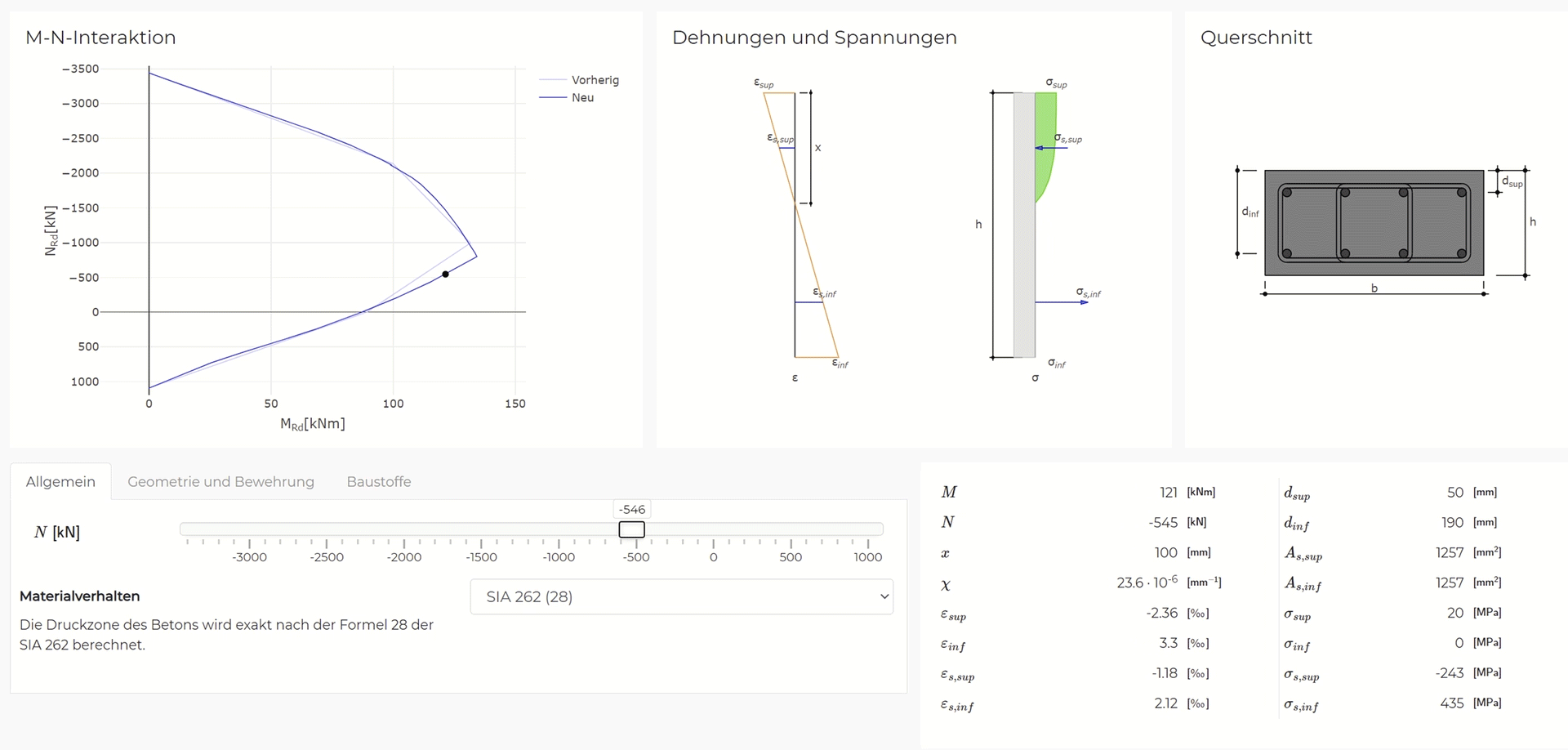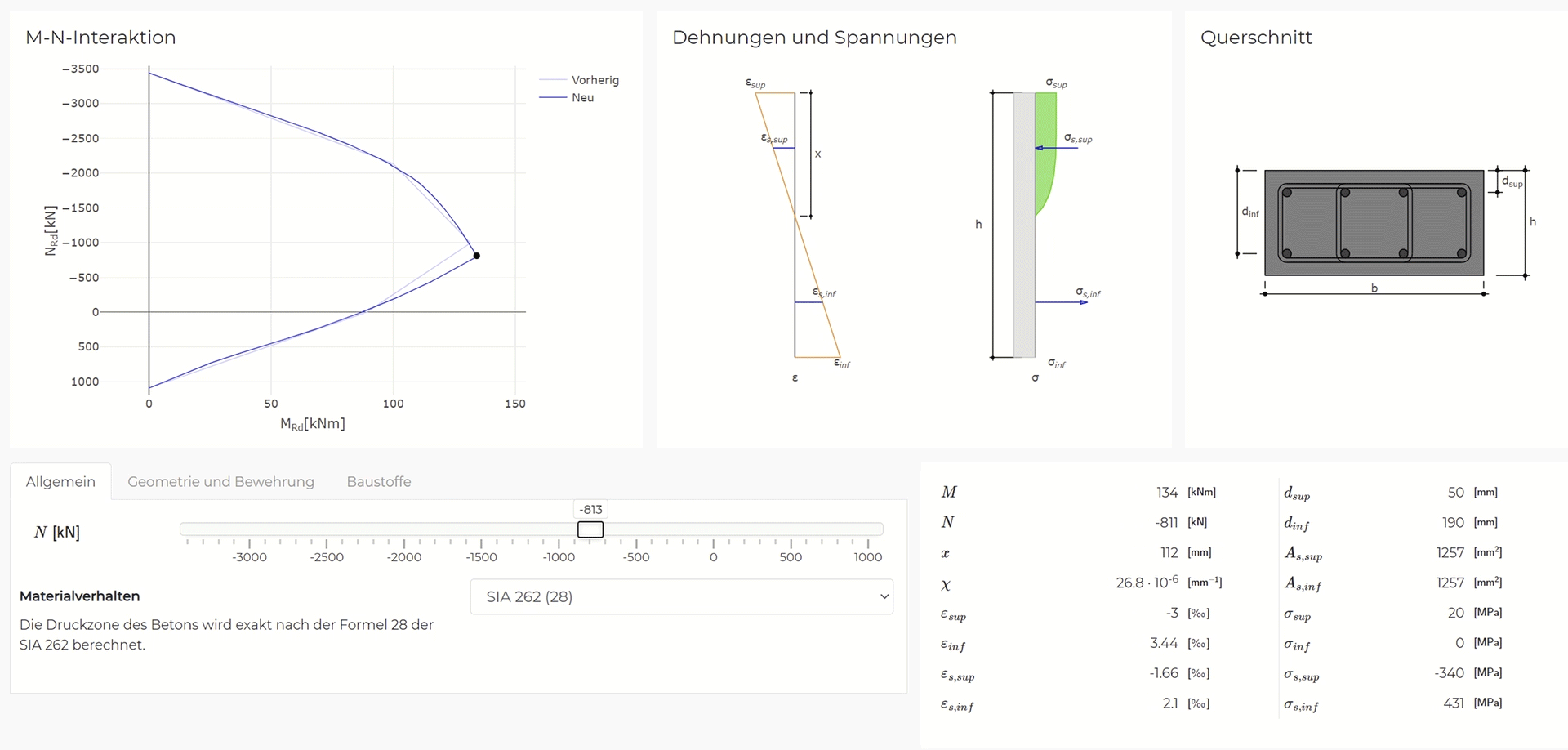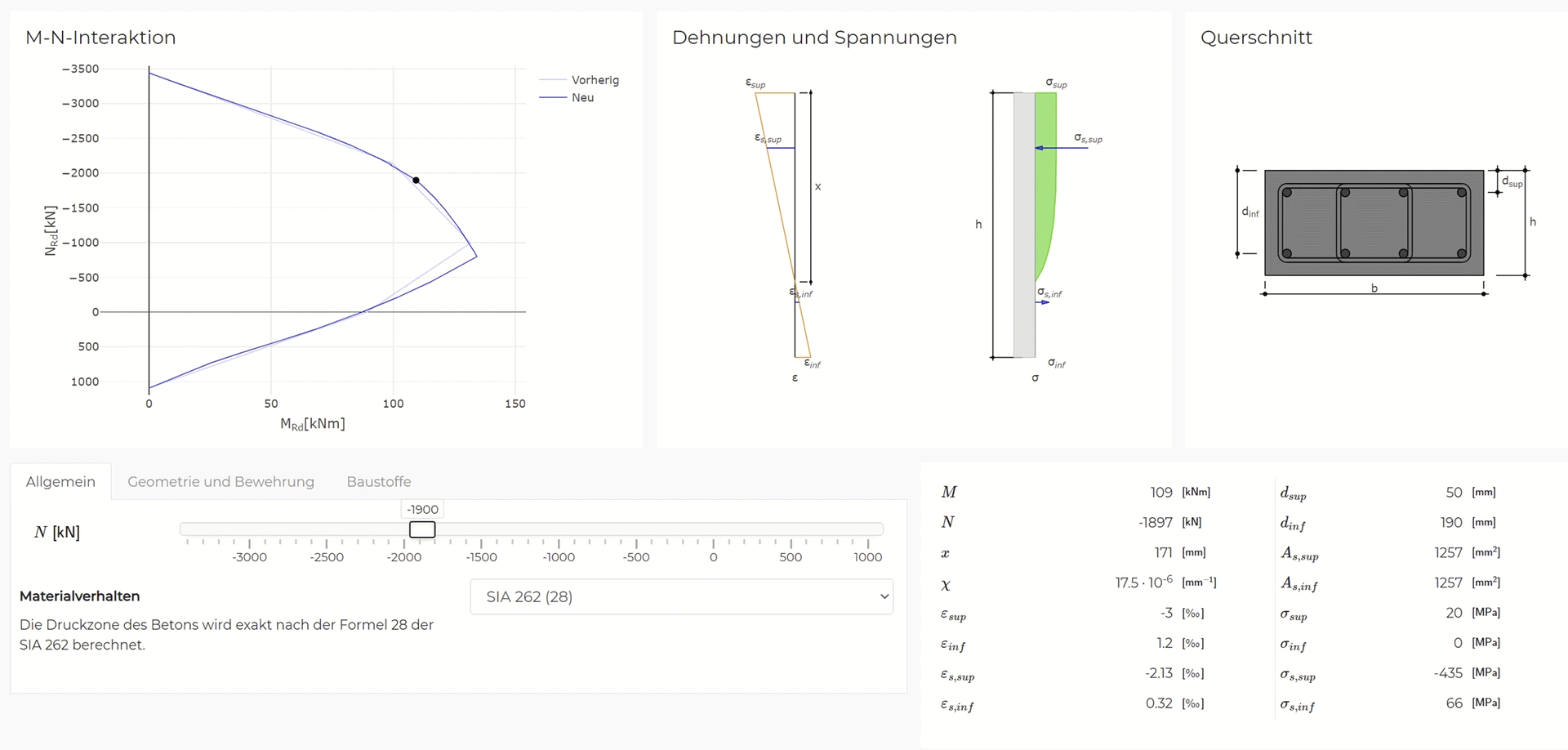
Nicht nur die Einwirkungen können verändert werden, sondern auch die Geometrie und die Bewehrung. So lässt sich zeigen, dass eine Verdoppelung des Bewehrungsgehalts eben nicht zu einer Verdoppelung des Biegewiderstands bei gegebener Normalkraft führt. Diese Erkenntnisse mögen trivial erscheinen. Wir sind jedoch überzeugt, dass bereits solch einfache Darstellungen und die kleinen Aha-Erlebnisse erheblich zum Verständnis beitragen und die Neugier der Studierenden für das effektive Verhalten von Stahlbeton, welches über das Berechnen von Grenzzuständen mithilfe starrer Formeln hinausgeht, fördern können.
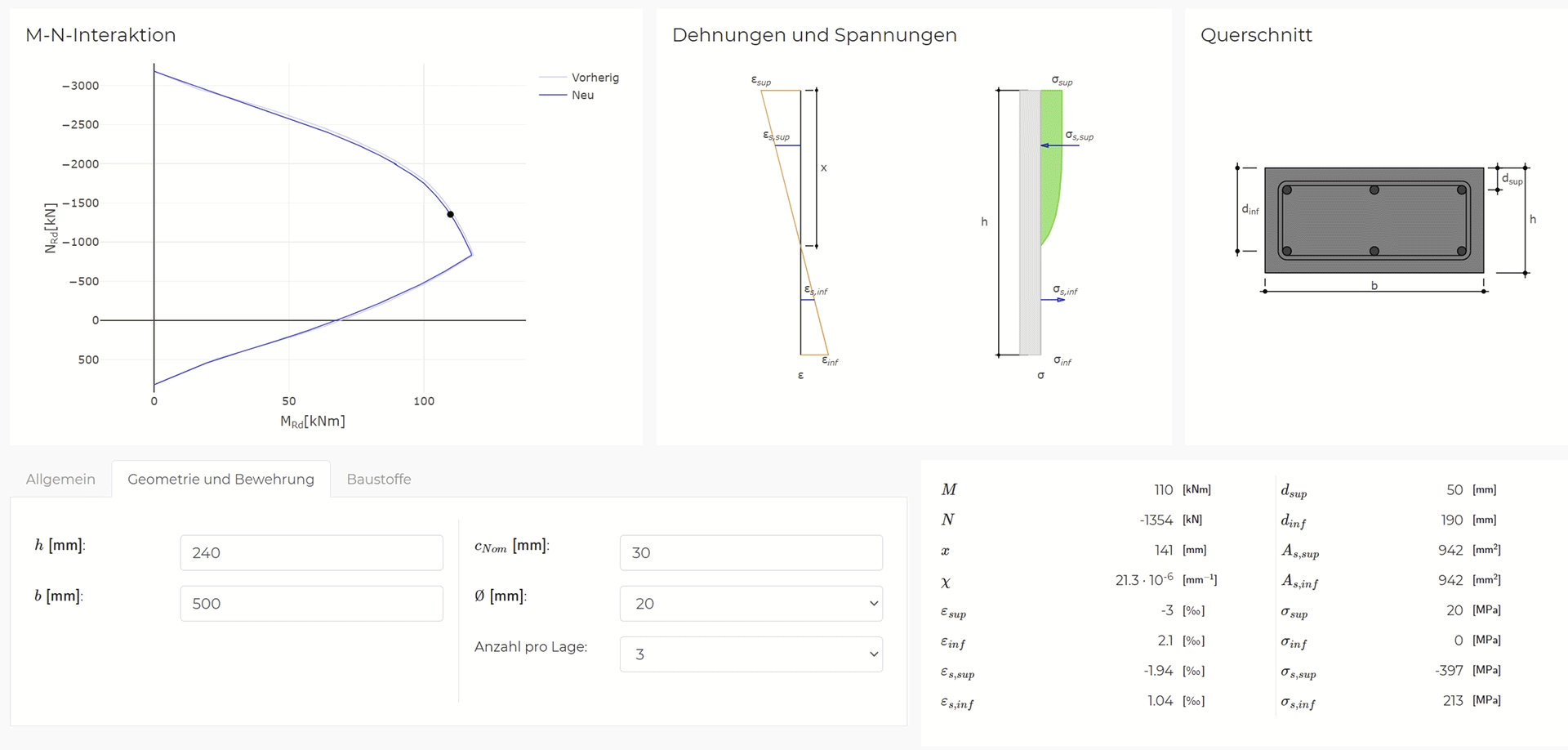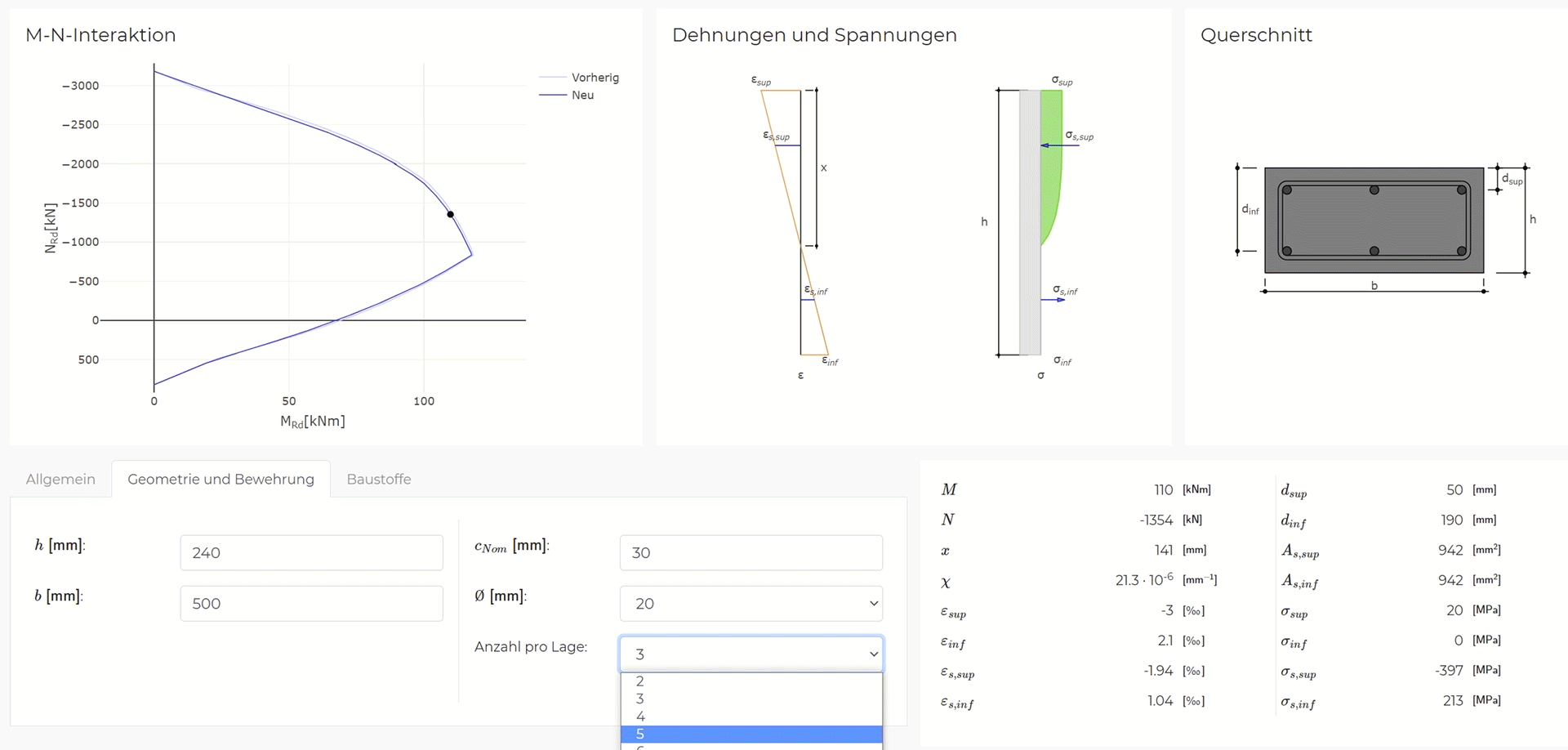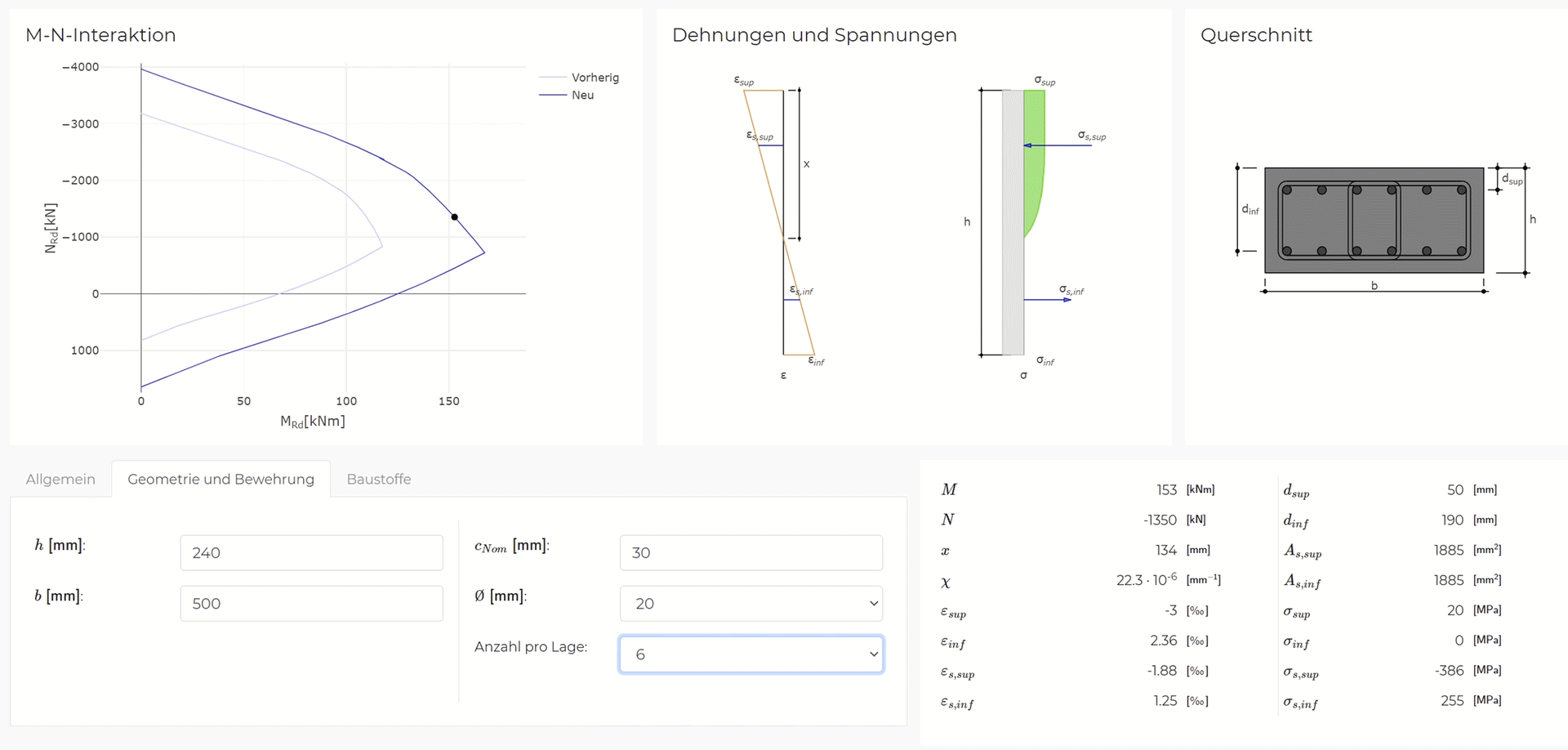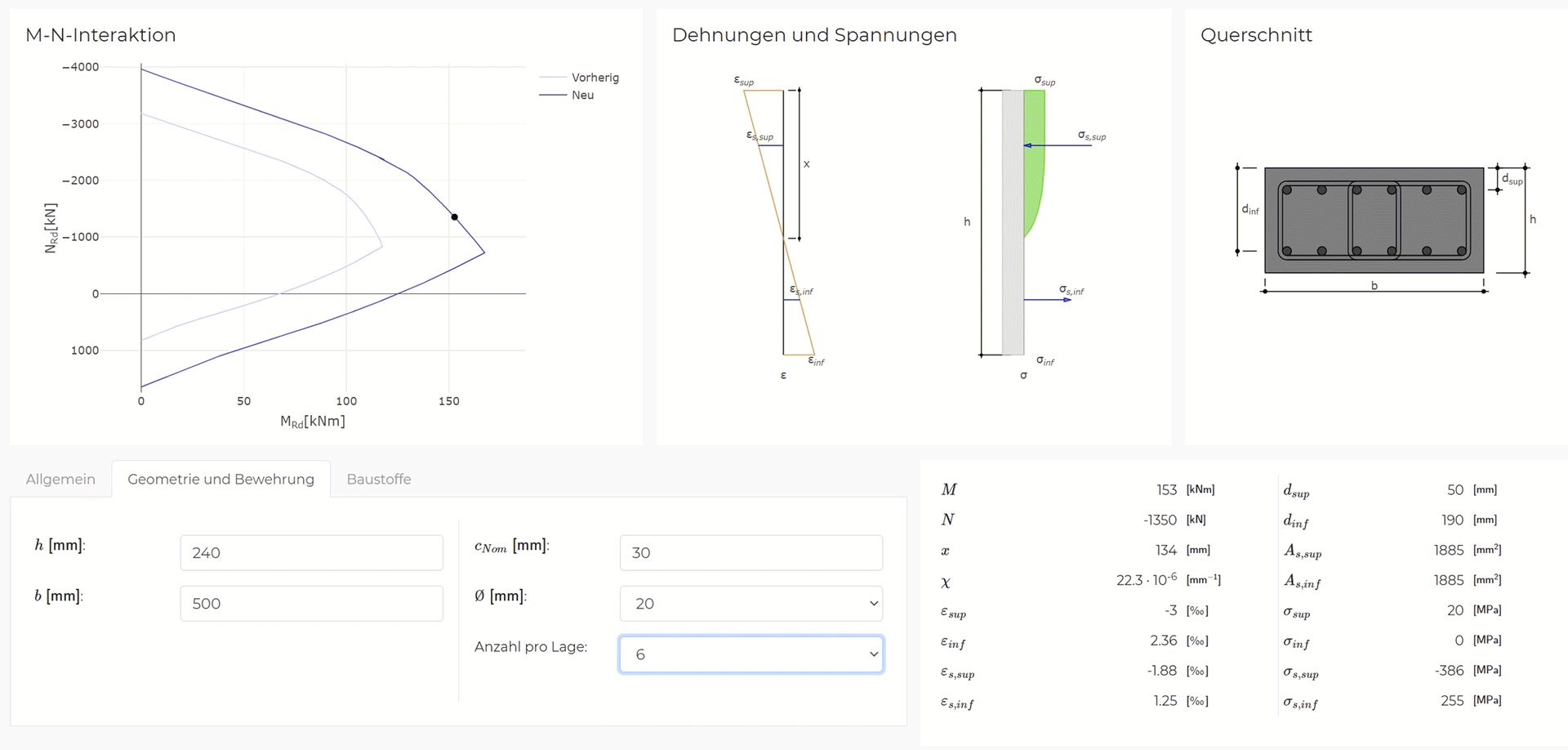
Die Applikationen sind zudem hilfreich für Problemstellungen, die wir grafisch lösen, deren händische Erarbeitung jedoch relativ aufwendig ist, insbesondere wenn mehrere Zustände betrachtet werden sollen. Dies zeigt sich beispielsweise bei den Fachwerkmodellen, wo die wandernde Einzellast über den Balken verschiedene Neigungen der Spannungsfelder erzeugt und deren Einfluss auf den inneren Lastabtrag untersucht werden kann. Das Potential dieser einfachen Visualisierungen zeigt sich in zahlreichen weiteren Anwendungen wie Mohrsche Kreise, Fliessbedingungen, dreidimensionale Bruchmechanismen in Platten und viele mehr.
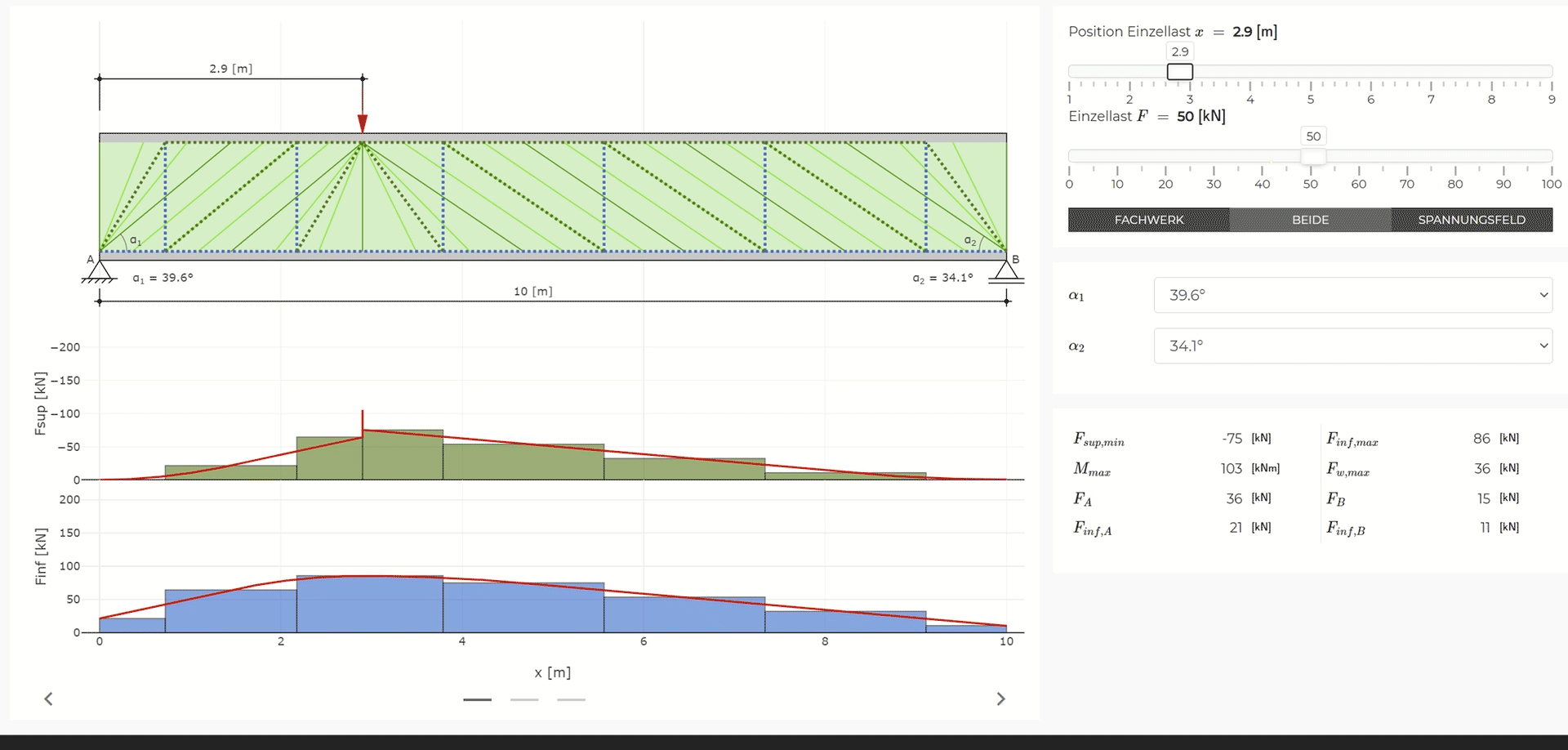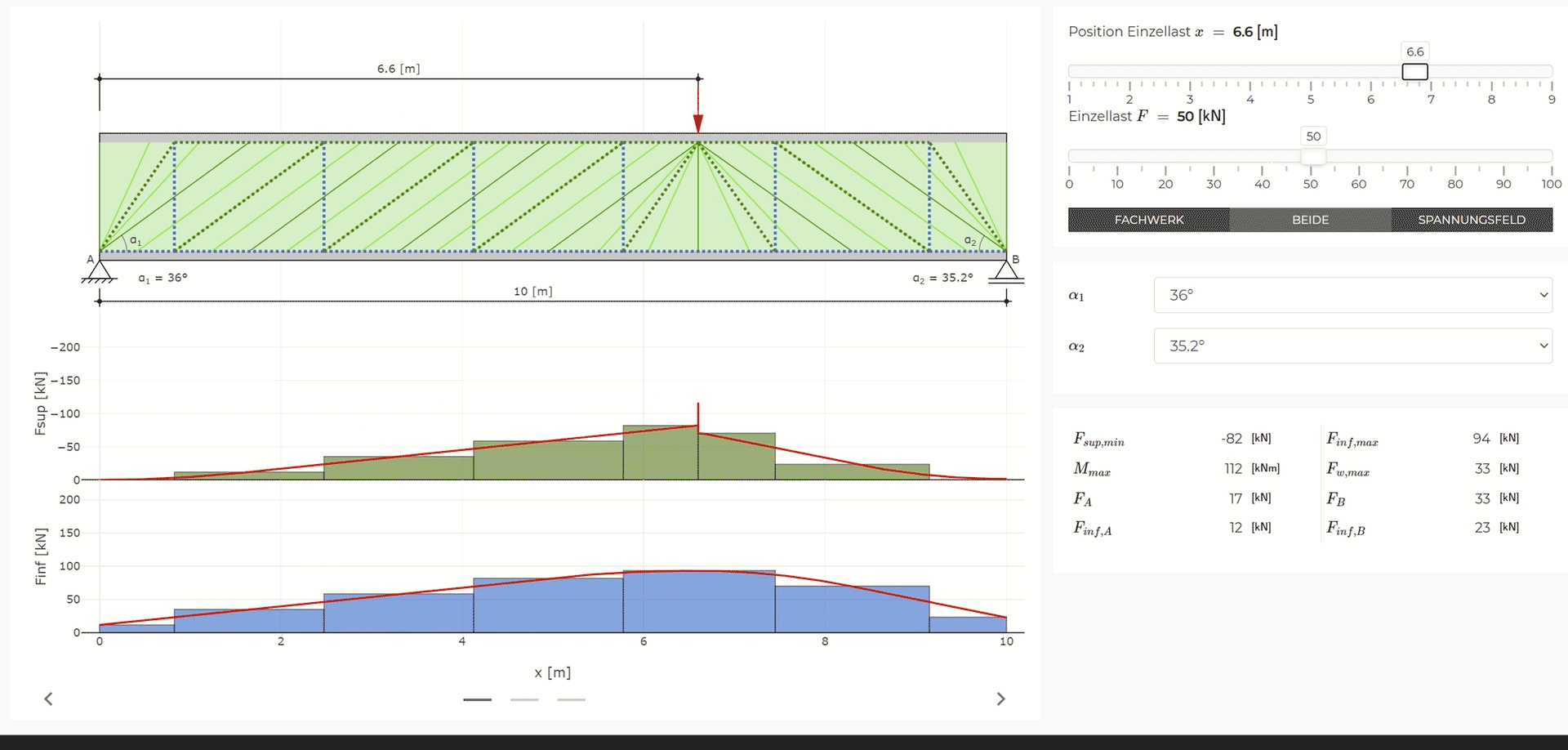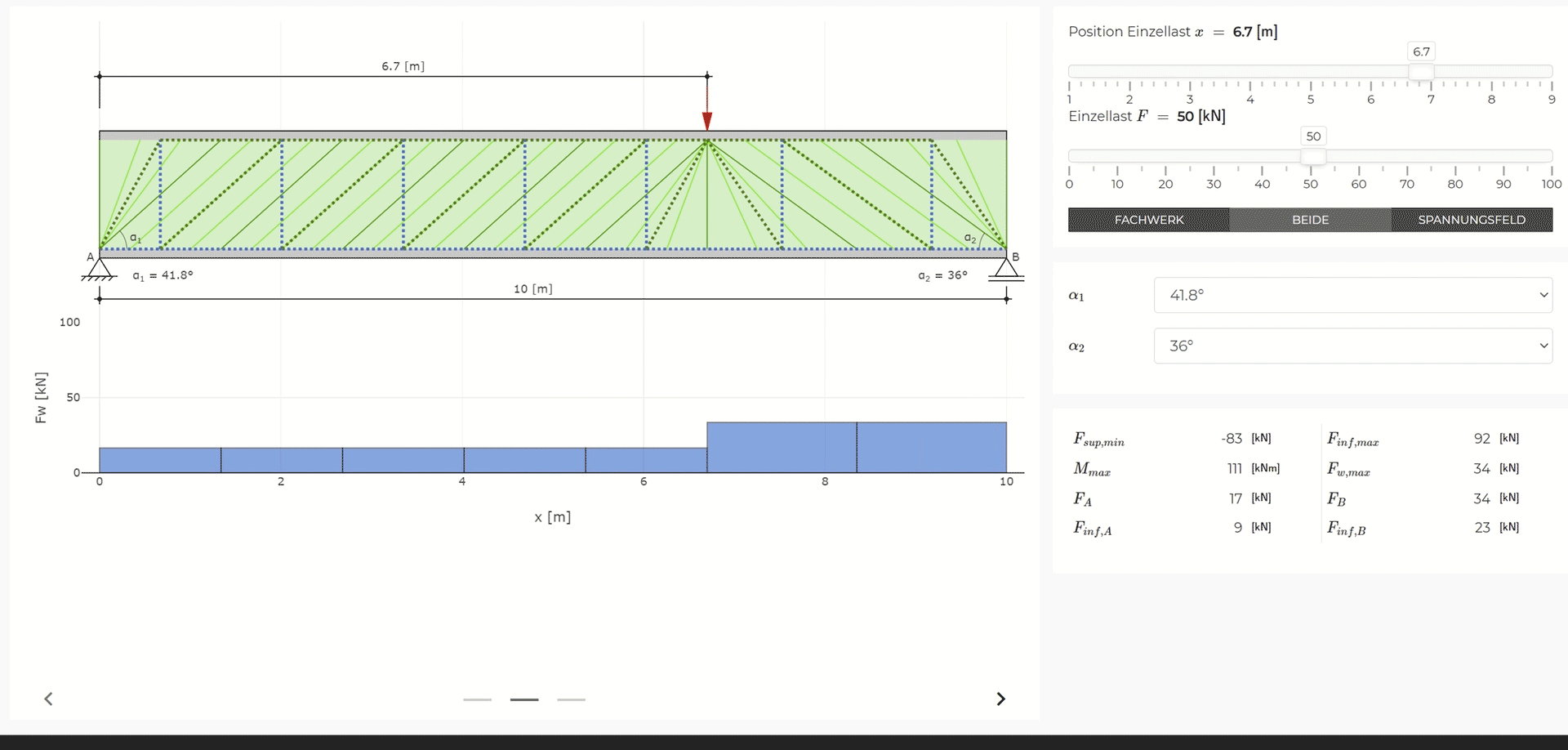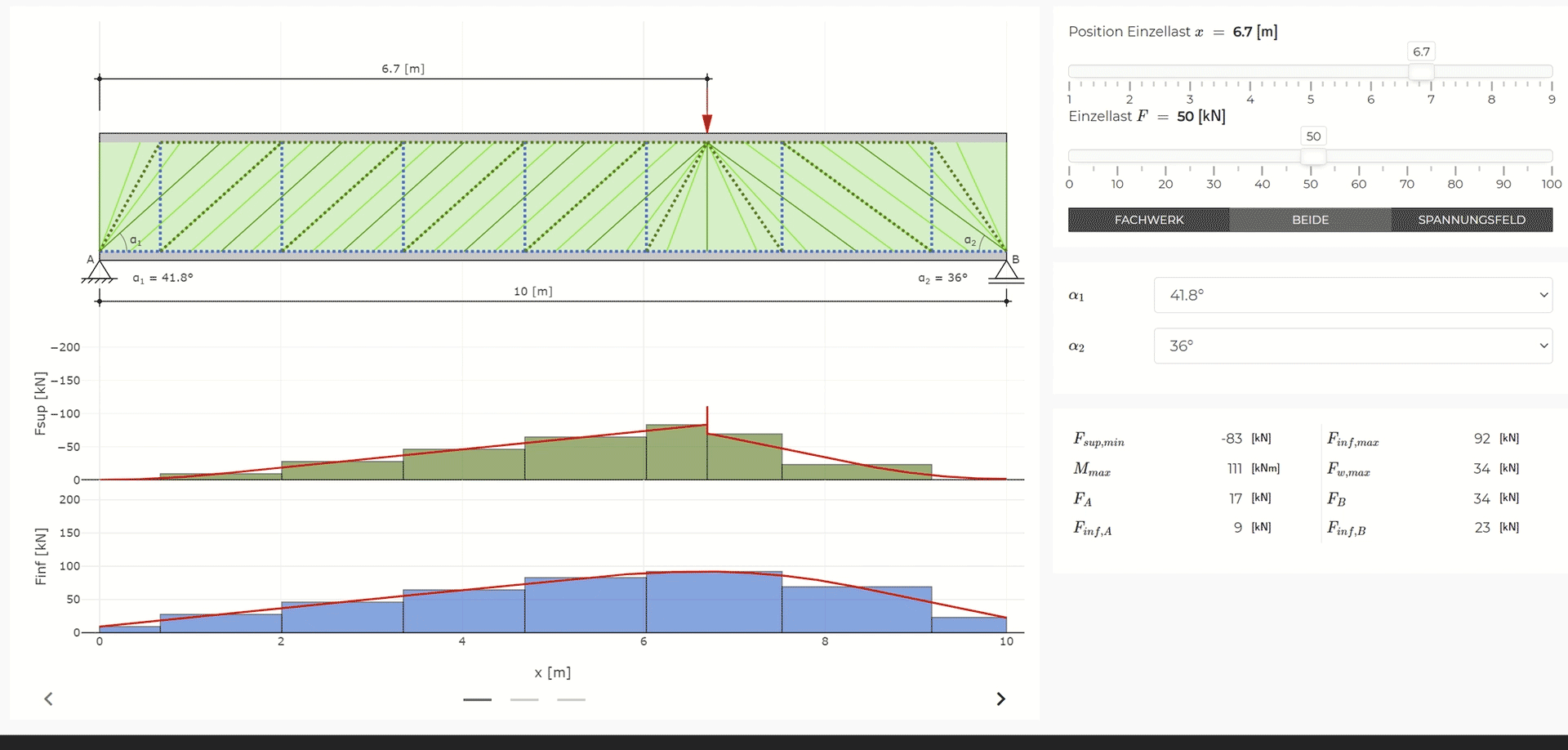
Die digitalen Lernapplikationen decken mittlerweile fast alle Themengebiete ab, welche wir im Stahlbeton behandeln, und sind somit ein ständiger Begleiter der Lehrveranstaltung. Sie bieten dabei vielfältige Vorteile: In der Vorlesung veranschaulichen sie beispielsweise neu eingeführte Themen oder sie erlauben in den Hausübungen effizientere Parameterstudien. Unser oberstes Ziel wäre schliesslich, dass die Studierenden auch unabhängig von gegebenen Aufgabenstellungen die Apps selbständig erkunden können, da das vermittelte Wissen nicht nur spezifisch für Stahlbeton sondern grundsätzlich für alle Arten von Baustoffen und Tragwerken anwendbar ist. Noch sind nicht alle Applikationen bezüglich des theoretischen Hintergrunds ausführlich dokumentiert. Wir sehen dies jedoch notwendig an, um eine Anwendung als reine Black Box zu vermeiden, und werden dies in der Zukunft noch weiter ergänzen.
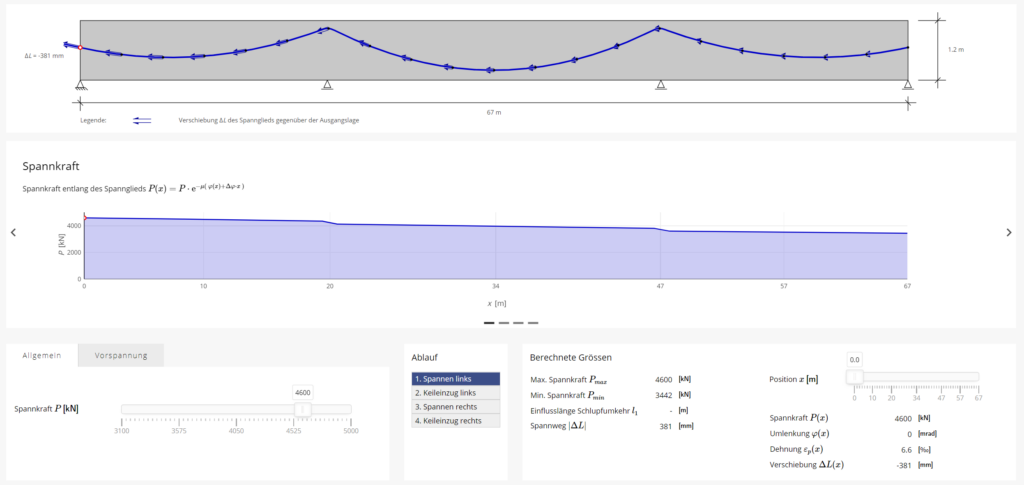
Die digitalen Apps wurden zudem ergänzt mit einigen physikalischen Modellen. Beispielsweise verwenden wir einen vorgespannten Balken, der aus Schaumstoffsegmenten besteht. Die Wirkung der Vorspannung und die Dekompression der Querschnitte können somit sowohl im physikalischen Modell als auch in der App dargestellt werden. In Zukunft möchten wir auch vermehrt reale Versuche aus unserer experimentellen Forschung den Simulationen gegenüberstellen. Denn auch diese virtuellen Experimente bleiben – wenn auch dynamisch und animiert – eine Modellvorstellung. Die Beobachtung von tatsächlich beanspruchten Bauteilen und Tragwerken gibt dabei eine bessere Vorstellung, was diese theoretisch formulierten Versagenszustände überhaupt in der Realität bedeuten.
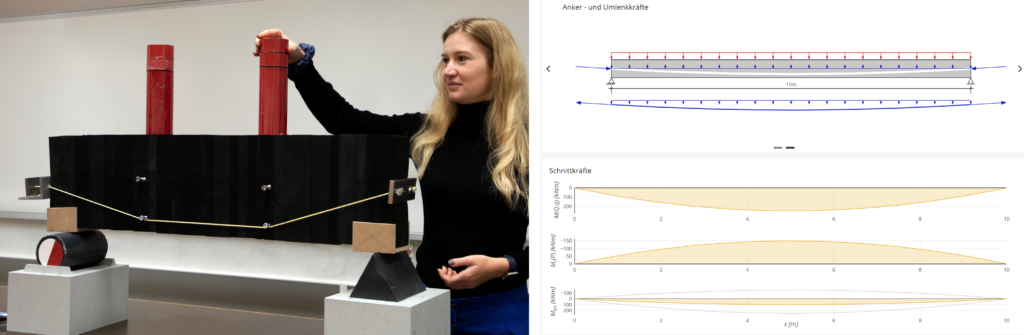
Herausforderungen in der Entwicklung und Implementierung
Die Entwicklung der Webapplikationen sowie deren Implementierung in den bestehenden Unterrichtsstoff stellten eine grosse Herausforderung dar. Unser Alltag ist bereits stark geprägt von digitalen Apps verschiedenster Art und insbesondere die digital native Generation hat hohe Ansprüche an die Nutzerfreundlichkeit. Für eine erfolgreiche Umsetzung war somit neben der fachlichen Ingenieurkompetenz auch das Webdesign ein prägender Faktor. Die Apps sollten im Erscheinungsbild wie auch in der intuititven Anwendung einen Wiedererkennungswert aufweisen. Gleichzeitig sollte die verwendete Plattform einen einfachen Einstieg ermöglichen, so dass die Applikationen auch von der zukünftigen Generation von Assistierenden stetig weiterentwickelt werden können. Die Erarbeitung der technischen Grundlagen verlangte daher einiges an Zeit und es waren mehrere Iterationen notwendig, bevor die erste App überhaupt programmiert werden konnte.
Wir hatten den Anspruch, dass die Webanwendungen als integraler Bestandteil des Unterrichts wahrgenommen werden, wobei wir diese nicht einfach als zusätzliches Element in einem bereits höchst umfangreichen Kurs einführen konnten. Gemäss einer Studierendenbefragung wurden die Applikationen als Darstellungsinstrument während der Vorlesung sehr geschätzt und auch in der Prüfungsvorbereitung wurden sie rege genutzt. Die Auseinandersetzung während des Semesters schien aber aufgrund fehlender Zeit eher gering zu sein. Dies bestärkte unser Bestreben, weitere Anpassungen in den Kolloquien und Übungen voranzutreiben, um die Anwendung im «alltäglichen» Gebrauch weiter zu fördern.
Fazit und weitere zukünftige Möglichkeiten
Die Entwicklung und Einführung digitaler Lernapplikationen eröffnete uns breitere Möglichkeiten unsere Lehrinhalte in der Vorlesung und in den Übungen zu gestalten, wobei wir vor allem Vorteile in der visuellen dynamischen Interaktion mit den Studierenden sehen. Dies ist nur ein erster Schritt in der Digitalisierung der Lehrinhalte und es gibt bereits viele weitere Ideen für neue innovative Unterrichtsmethoden wie beispielsweise die Anwendung von Augmented Reality (Vermischung von realer Umgebung mit digitalen Inhalten) im Brückenentwurf. Nach wie vor sind wir aber überzeugt, dass das Fundament unserer Lehre im Stahlbetonbau auf der konsequenten Anwendung des Gleichgewichts und mechanisch konsistenter Modelle beruht. Dafür sehen wir ganz klar Papier und Stift als die besten Werkzeuge an. Trotzdem möchten wir Sie einladen, die Applikationen einmal selber zu erkunden. Denn es gibt auch im Stahlbeton-Einmaleins – sei es im Studium, in der Praxis oder in der Forschung – immer wieder Neues zu entdecken.
Danksagung
Dieses Lehrprojekt wurde durch den Innovedum-Fonds der ETH Zürich unterstützt. Ein grosser Dank gilt allen Beteiligten, welche zur Umsetzung der Applikationen beigetragen haben.
Projektverantwortliche: Prof. Dr. Walter Kaufmann, Minu Lee
Webdesign und Entwicklung: Sebastian Wehrli
Applikationen: Lukas Gebhard, Nicola Gehri, Nathalie Reckinger
Revision: Fabian Morger, Andreas Näsbom
Links
Sammlung aller Stahlbeton-Lernapplikationen:
https://concrete.ethz.ch/applikationen/
Learning and Teaching Fair:
https://learning-teaching-fair.ethz.ch/project/visual-interactive-learning-applications/?view=grid
Innovedum-Projektdatenbank:
https://ethz.ch/en/die-eth-zuerich/lehre/innovedum/projektdatenbank.html
Minu Lee
Link to English version: Reinforcement affected by local corrosion – minor damage with significant consequences
Die Bewehrung vieler älterer Bauwerke korrodiert. Die Gründe hierfür sind vielfältig und reichen von der Karbonatisierung des Betons über das Eindringen von Chloriden bis hin zu undichtem Überdeckungsbeton. Das Schadenspotential ist gerade bei lokaler Korrosion der Bewehrung (bspw. Lochfrasskorrosion infolge von Chloriden oder undichter Überdeckung) beträchtlich, da die Korrosionsgeschwindigkeit durch Makroelementbildung sehr hoch ist (Querschnittsabtrag typischerweise im Bereich von 1 mm pro Jahr). Doch welche Auswirkungen haben lokale Korrosionsschäden eigentlich auf die Tragfähigkeit und das Verformungsvermögen betroffener Bauwerke? Davon handelt dieser Blogbeitrag.
Versteckter Schaden – grosse Unsicherheit
Eine Pilotstudie des Bundesamtes für Strassen ASTRA ergab, dass die Bewehrung vieler Winkelstützmauern entlang der Autobahnen, welche in den 1960er und 1970er Jahren gebaut worden sind, korrodiert. Im Schnitt wiesen rund 36% der untersuchten Bewehrungsstäbe Korrosionsschäden auf, der Querschnittsverlust der betroffenen Stäbe betrug im Mittel 25%. Betroffen ist die hangseitige Biegebewehrung oberhalb der Arbeitsfuge zwischen Fundament und aufgehender Wand. Die plausibelste Ursache für die lokale Korrosion sind Kiesnester, also undichter Überdeckungsbeton, infolge unsauberen Einbringens und Verdichtens des Wandbetons, ohne massgeblichen Einfluss von Chloriden.

Die Detektion der Korrosion bei diesen Bauwerken erwies sich in der Pilotstudie als äusserst schwierig. Die Stärke der Mauern oberhalb des Fundaments war zu gross, als dass mit bekannten Messverfahren von der Luftseite her eine zuverlässige Aussage zum Zustand der hangseitigen Bewehrung gemacht werden konnte. Das Schadensausmass zeigte sich erst durch die visuelle Inspektion der Bewehrung, d.h. nach vorgängigem Erstellen von Schächten hinter der Mauer und Abtrag des (schadhaften) Überdeckungsbetons.
Aufgrund der entstandenen Unsicherheit hinsichtlich Anzahl betroffener Stützmauern und deren Tragverhalten startete das ASTRA zusammen mit dem Bundesamt für Verkehr BAV (auch die Bahn hat viele Winkelstützmauern) fünf Forschungsprojekte, wovon wir eines bearbeiten dürfen. Dieses Projekt befasst sich mit dem Tragverhalten und Verformungsvermögen von Winkelstützmauern mit lokal korrodierender Bewehrung. Eine erste Einschätzung im Rahmen des Projekts ergab, dass die Tragfähigkeit der Stützmauern überproportional verringert sein dürfte (also stärker als wenn lediglich der vorhandene Verlust an Bewehrungsfläche betrachtet wird). Zudem ist das Verformungsvermögen durch die lokale Schädigung drastisch reduziert. Letzteres ist insbesondere von Relevanz, da diese Mauern nach der damaligen Normengeneration häufig nur auf aktiven Erddruck bemessen wurden. Dies setzt jedoch eine Verformung der Wand und damit ein ausreichendes Verformungsvermögen im Grenzzustand der Tragsicherheit voraus. Ist das Verformungsvermögen reduziert, so ist neben der verminderten Tragfähigkeit zudem von einer erhöhten Einwirkung (im Extremfall dem Erdruhedruck) auszugehen – eine unschöne Ausganglage für eine Überprüfung.
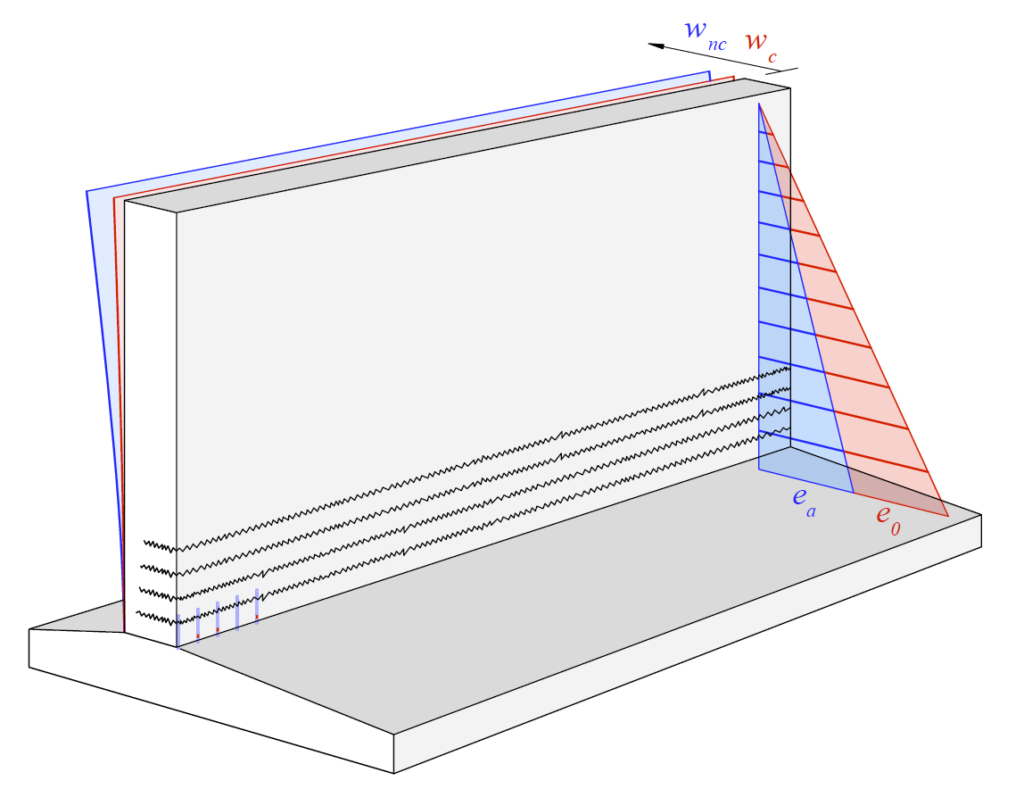
Lokale Korrosion – vielfältige Auswirkungen
Die Forschung hat erkannt, dass die Schädigungsgeometrie (Morphologie) das Verhalten eines Bewehrungsstabs rund um die Korrosionsstelle massgebend beeinflusst. Infolge der lokalen Verjüngung laufen die Spannungstrajektorien zusammen, es entsteht ein inhomogener, dreidimensionaler Spannungszustand im Querschnitt. Die am ungeschädigten Bewehrungsstab ermittelten Materialkennlinien verlieren ihre Gültigkeit.
Durch die Verschiebung der Neutralachse bei einseitig geschädigten Stäben – eine bei Lochfrass häufig vorkommende Schädigungsgeometrie – entstehen zudem lokal Biegemomente, welche der Zugbelastung superponiert werden müssen. Das zusätzlich einwirkende Biegemoment reduziert sich zwar mit zunehmender Plastifizierung des Stahls (es bildet sich ein lokales Fliessgelenk), durch die grosse Krümmung wird aber die Bruchdehnung vergleichsweise früh erreicht. Dies kann zu einem vorzeitigen Versagen führen, wie experimentelle Untersuchungen im Rahmen dieses Projekts gezeigt haben.
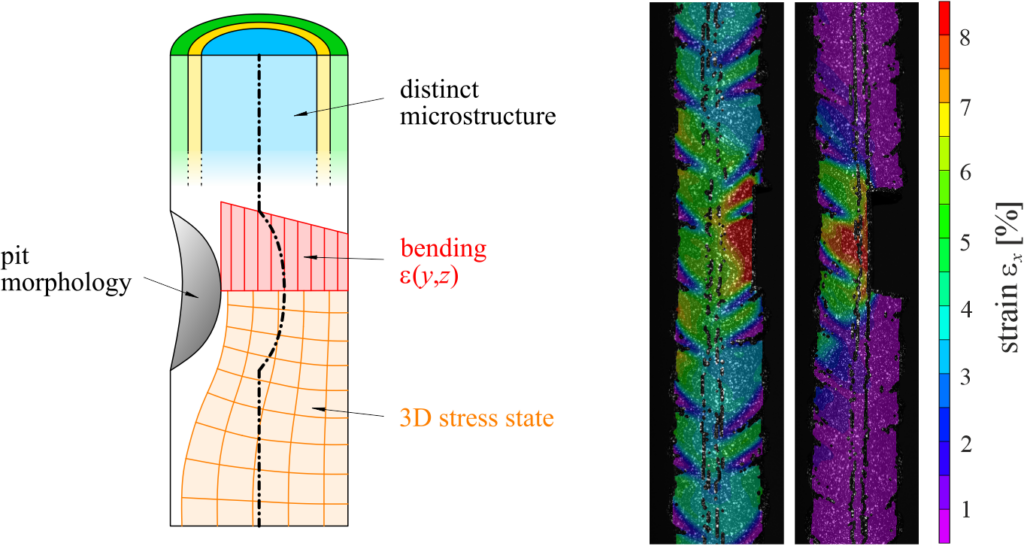
Seit Ende der 1970er Jahre wird ein Grossteil des Bewehrungsstahls weltweit im sog. «Tempcore-Verfahren» hergestellt (warmgewalzt und aus der Walzhitze vergütet), so auch in Europa. Der Querschnitt dieser Stäbe besteht aufgrund des Produktionsprozesses aus drei verschiedenen Materialschichten, welche unterschiedliche Eigenschaften aufweisen. Wenn ein Tempcore-Stab korrodiert, so ändert er aufgrund seines schichtweisen Aufbaus mit fortschreitendem Materialverlust laufend seine mechanischen Eigenschaften. Insbesondere nimmt seine Festigkeit kontinuierlich ab, da das Kernmaterial gegenüber dem Mantel eine fast 30% geringere Festigkeit aufweist.
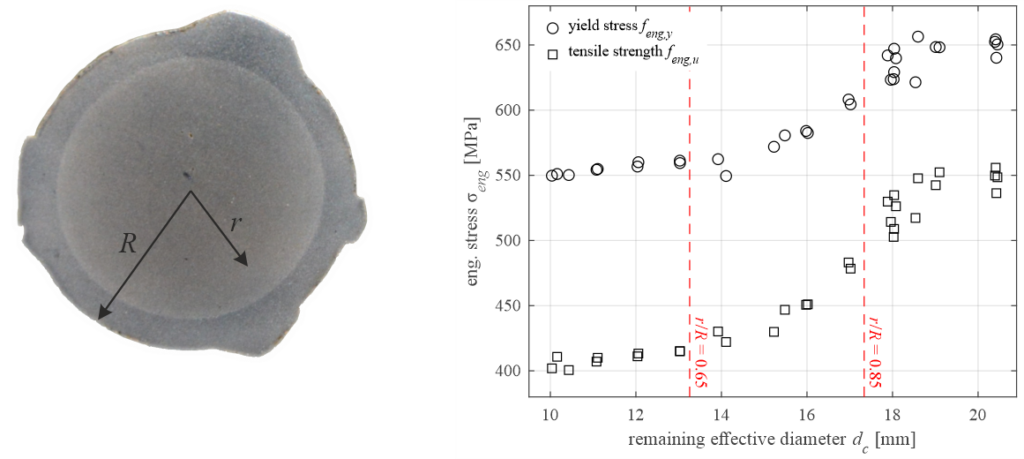
Die Schädigung eines Bewehrungsstabes über eine kurze Länge erweist sich für sein Verformungsvermögen als äusserst ungünstig. Der Stab dehnt sich insbesondere im geschwächten Bereich, die Verformung lokalisiert sich (engl.: strain localisation). Kritisch wird es spätestens dann, wenn der geschädigte Querschnitt vor dem Bruch nicht mehr genügend Kraft übertragen kann, um die daran anschliessenden, ungeschädigten Stabbereiche ins Fliessen zu bringen. Der Stab hat dann praktisch sein gesamtes plastisches Verformungsvermögen verloren. Für heutige Stäbe aus europäischer Produktion ist dieser Punkt bereits bei kleinen Querschnittsverlusten zwischen 12% und 20% erreicht (zur Erinnerung: der mittlere Querschnittsverlust in der Pilotstudie des ASTRA betrug 25%). Erschwerend kommt hinzu, dass der kritische Schnitt bei den Stützmauern am Rand eines Bewehrungsstosses liegt (die Bewehrung wurde typischerweise oberhalb der Arbeitsfuge gestossen). Dies ist eine Zone mit ohnehin eingeschränktem Verformungsvermögen, wie eine neue, noch unveröffentlichte Studie zeigt.
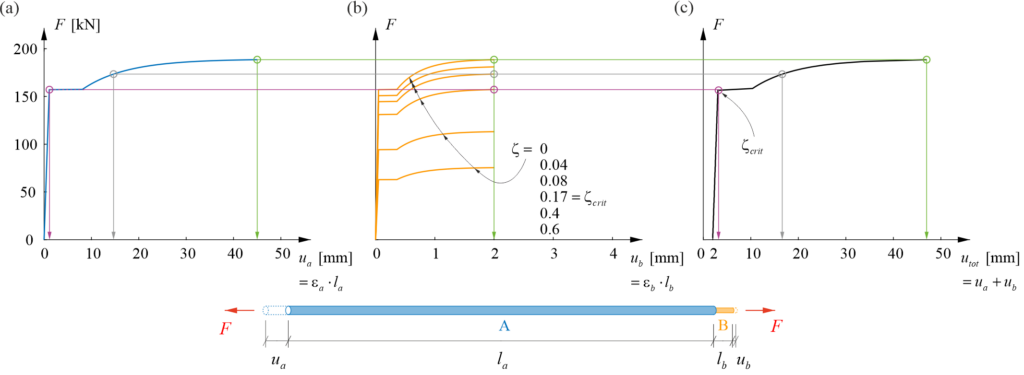
Forschung im Kleinen – und im Grossen
Neben mehr als 100 Zugversuchen an Bewehrungsstäben mit unterschiedlichsten Schädigungsgeometrien wurden im Rahmen dieser Forschungsarbeit auch 8 Grossversuche an Stützmauerausschnitten im Large Universal Shell Element Tester LUSET durchgeführt. Die Wände waren 2.0 m breit, 1.7 m hoch, 0.38 m stark und standen auf Fundamenten mit Abmessungen von 2.1 x 0.4 x 1.4 m. Die mehr als sechs Tonnen schweren Elemente repräsentierten den untersten Teil einer 4.7 m hohen Stützmauer und wurden im LUSET am Elementkopf mit einer entsprechenden Kombination aus Normal- und Querkraft sowie dem in dieser Höhe wirkenden Biegemoment belastet.
Die Wandelemente wurden mit modernster Messtechnik instrumentiert. Mittels faseroptischer Dehnungsmessung konnte die Spannung in der Bewehrung ermittelt und alle paar Millimeter dargestellt werden. Ein dreidimensionales Bildkorrelationssystem (DIC) gab Aufschluss über die Verformung der Wand sowie die Kinematik der entstandenen Risse mit einer Genauigkeit von einigen Hundertstel Millimetern.

Um den Einfluss des Querschnittsverlusts infolge Korrosion zu untersuchen, wurden einzelne Bewehrungsstäbe vorgängig mechanisch mit einem Radiusfräser von 20 mm Durchmesser auf Höhe der Arbeitsfuge geschädigt. Diese Art von «künstlicher Korrosion» führt, wie vorgängige Versuche in Zusammenarbeit mit Prof. Dr. Ueli Angst gezeigt haben, zu unwesentlich anderem Verhalten als eine «natürliche» elektrochemische Korrosion. In drei Hybridversuchen wurden vier (von 10) Bewehrungsstäbe direkt während des Versuchs mit am Fundament befestigten, vollautomatisch gesteuerten Bohrmaschinen schrittweise geschädigt. Mit Hilfe eines Modells des Instituts für Geotechnik (Prof. Dr. Alexander Puzrin, David Perozzi), welches den Erddruck in Abhängigkeit der Wandverformung simulieren kann, wurde die aufgebrachte Last unter Einbezug der gemessenen Wandkopfverschiebung fortlaufend aktualisiert und der Versuchskörper so realitätsgetreu belastet.
Was wir nun wissen – und was noch nicht
Die Traglast von Bauteilen mit lokal korrodierter Bewehrung ist überproportional reduziert, dies infolge lokaler Phänomene rund um die Korrosionsstelle. Berechnungsmodelle, die lediglich den Querschnittsverlust berücksichtigen, überschätzen daher die tatsächlich vorhandene, verbleibende Traglast.
Eine lokale Schwächung der Bewehrungsstäbe führt bereits bei kleinen Querschnittsverlusten zu einem drastisch eingeschränkten, um bis zu 85% geringeren Verformungsvermögen eines Bauteils. Damit sind sämtliche Modelle, die auf dem unteren Grenzwert nach der Plastizitätstheorie basieren, – also die Mehrheit der Normnachweise – nicht mehr uneingeschränkt gültig, und das tatsächliche Verformungsvermögen muss im Detail untersucht werden.
Die Resultate der durchgeführten Versuche an Bewehrungsstäben und Stützmauerausschnitten belegen obige Aussagen eindrücklich. Die innerhalb dieses Forschungsprojekt entwickelten Modelle – ausgehend von einer Erweiterung des Zuggurtmodells – bilden einen vielversprechenden Ansatz zur Beschreibung des verbleibenden Last-Verformungs-Verhaltens von Bauteilen mit lokaler Bewehrungskorrosion. Sie können sowohl für die Überprüfung von Winkelstützmauern wie auch von anderen Bauteilen, für welche das Verformungsvermögen relevant ist (bspw. Brückenquerschnitt über Mittelauflager), herangezogen werden.
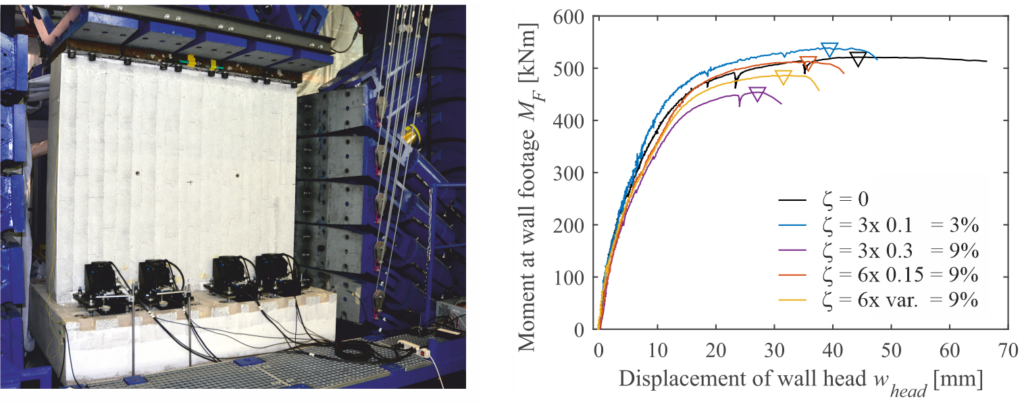
Eines der Ziele dieses Projekts ist die Erarbeitung von (vereinfachten) Überprüfungsregeln für die Praxis. Wie genau diese ersten Forschungsresultate von Ingenieuren, die mit der Überprüfung solcher Bauwerke betraut sind, genutzt werden können, wird derzeit noch diskutiert. Der Fokus hierbei sind u.a. die Folgen einer nur sehr eingeschränkt möglichen Detektion von Korrosionsschäden, sowie ob und wie die Beobachtungsmethode angewandt werden könnte, um korrodierende Stützbauwerke weiterhin sicher betreiben zu können.
Ob filigrane Stützbauwerke tatsächlich «passé» sind, wie der Titel eines Interviews im Tec21 (40/2016) lautete, ist am Ende eine Entscheidung der Bauherrschaft. Die Exposition ist grundsätzlich moderat (Erdkontakt, wechselfeucht, ohne Chloride), und bei korrekter Bauweise (d.h. Anbringen einer sog. «Kickerschalung» und gute Verdichtung des Wandbetons, allenfalls Abkleben der Betonierfuge) sind solche Bauwerke grundsätzlich nicht stärker korrosionsgefärdet als andere, vergleichbare Bauteile. Ein genereller Paradigmenwechsel zu massiven Schwergewichtsmauern, mit entsprechend hohem Ressourcenverbrauch und Treibhausgasemissionen, scheint aus unserer Sicht jedenfalls nicht angezeigt zu sein.
Severin Haefliger
Link to English version: Building curved concrete walls without formwork
Beton ist heutzutage bei weitem das meistgenutzte Baumaterial. Die Möglichkeit ihn in jede mögliche Form zu giessen hat sicher zu seinem Erfolg beigetragen. Von frühen Anwendungen im römischen Reich bis heute wird Beton typischerweise in eine Schalung gegossen. Kennen Sie aktuelle Forschung um Schalungen bei Bau von Betonstrukturen zu vermeiden? In diesem Post stelle ich die neusten Fortschritte in der digitalen Fabrikation mit Beton vor, mit einem speziellen Fokus auf das schalungslose Verfahren Mesh Mould Prefabrication. Neue digitale Technologie eröffnet den Weg zur nachhaltigeren Herstellung von optimierten, geometrisch komplexen Bauwerken und könnte bald standardmässig auf Baustellen verwendet werden.
Schwachpunkte konventioneller Schalung für komplexe Geometrien
Auf dem Markt gibt es eine Fülle industrieller Schalungssysteme, die es erlauben Betonstrukturen mit einfachen oder wiederholenden Formen effizient zu bauen. Der Anteil solcher Schalungen an der totalen Umwelteinwirkung und an den Kosten des Bauwerks ist üblicherweise begrenzt, da sie mehrmals wiederverwendet werden können. Bei geometrisch komplexen Bauwerken sieht das grundlegend anders aus. Solche Bauwerke benötigen oft sehr teure Unikate als Schalung, die oft nicht wiederverwendet oder sogar nicht recycelt werden können.

Bildquelle: Fabian Scheurer, designtoproduction. 
Bildquelle: INGPHI.
Die Bilder zeigen, dass der Bau von geometrisch komplexen Bauwerken mit Einwegschalungen alles andere als wirtschaftlich und nachhaltig ist. Daraus folgt, dass nur einzigartige Projekte sich heute komplexe Geometrien, wie zum Beispiel doppelt gekrümmte Oberflächen, leisten können. Viele von Ihnen denken wahrscheinlich, dass solche Bauwerke ein Nischenprodukt sind, das nur ästhetische Zwecke erfüllt. Warum sind wir dann daran interessiert sie effizienter zu bauen? Wir haben früher verwendete statische System mit effizientem Tragverhalten zugunsten von effizienten Bauabläufen aufgegeben. Unser oberstes Ziel ist es die Herstellung von materiell optimierten Betonbauwerken erschwinglich und nachhaltig zu machen, nicht nur extravagante Entwürfe zu ermöglichen.
Wie die Digitale Fabrikation den Betonbau verändern kann
Die zunehmende Digitalisierung im Bauwesen bietet viele Möglichkeiten um die Herausforderung von Betonbauten mit komplexer Geometrie zu gleichen Kosten und sogar mit weniger Bauabfall anzugehen. Das Forschungsgebiet heisst Digitale Fertigung mit Beton und deckt eine Vielzahl Themen ab, von robotisch hergestellter Bewehrung über die additive Fertigung von Beton bis zu rechnergestützten Entwurfstools für komplexe Geometrien. Dank unserer Beteiligung am Nationalen Forschungsschwerpunkt (NFS) Digitale Fabrikation ist unsere Gruppe in diesem Gebiet sehr aktiv. In einem zukünftigen Post werde ich das breite Spektrum an Technologien der digitalen Fabrikation, die zur Erstellung von Betonbauten genutzt werden können, vorstellen. Die Verfahren sind entweder schalungsfrei oder sie nutzen keine herkömmliche Schalung. Vielleicht haben Sie schon vom 3D-Druck mit Beton gehört, der meisterforschten Methode der digitalen Fabrikation. Dabei wird ein Betonelement schalungsfrei produziert indem Betonschichten übereinander extrudiert werden.

Dank grossen Entwicklungen in der Materialwissenschaft und –technologie hat der 3D-Druck mit Beton einen hohen Grad der Automatisierung erreicht. Die Herstellung von Betonbauten mit 3D-Druckverfahren ist jedoch noch eine Herausforderung, da es noch keine geeignete Strategie zur Integration der Bewehrung gibt, insbesondere in die Druckrichtung. High-tech 3D-gedruckte Wände sind bis jetzt üblicherweise unbewehrt und auf sehr geringe Einwirkungen ausgelegt (typischerweise einstöckige Gebäude, wie in den Bildern unten). Sie hätten mit viel tieferen Kosten und Umwelteinwirkungen in Mauerwerk gebaut werden können.

Suite im Lewis Grand (Baradi 2016). 
R&Drone Laboratory in Dubai (Cybe 2017). 
Apis Cor Haus in Russland (Skin 2017). 
Apis Cor Haus in Russland (Skin 2017). 
3D HOUSING 05 in Mailand (CLS 2018). 
Das BOD in Kopenhagen (COBOD 2018).
Mesh Mould: Beginn der Forschungsarbeiten
Mesh Mould ist ein weiterer digitaler Fabrikationsprozess und löst die Problematik der Integration von Bewehrung, die bei anderen Technologien, wie zum Beispiel 3D-Druck mit Beton, besteht. Mesh Mould erlaubt es effizient doppelt gekrümmte tragende Wände zu erstellen. Gramazio Kohler Research an der ETH Zürich kam bereits vor einem Jahrzehnt auf das Konzept, als Weiterentwicklung des Ferrocement Systems, das Pier Luigi Nervi 1943 patentiert hat, mit innovativen digitalen Prozessen.
The formwork which represents the real weakness of reinforced concrete from a constructive and economic viewpoint becomes absolutely superfluous with ferrocement. The metal reinforcement made up of netting and bars can adapt with great ease to curved surfaces or any type of skewing. Its intrinsic lightness and deformability mean that it can be supported with light scaffolding, which enormously simplifies the construction of large and very large roofs
P. L. Nervi: “Scienza O Arte Del Costruire?: Caratteristiche E Possibilità Del Cemento Armato”, 1945
Bei Mesh Mould produziert ein Roboter ein dichtes Bewehrungsnetz. Das Netz wird mit einer speziellen Betonmischung befüllt, die eine genügende Verdichtung erreicht, ohne aus dem Netz zu fliessen.
Schliesslich wird die Bewehrungsüberdeckung mit Spritzbeton aufgetragen. Obwohl wir Mesh Mould oft als schalungslose Bauweise bezeichnen dient die Bewehrung strenggenommen als durchlässige verlorene Schalung. Die geometrische Freiheit von Wänden, die mit diesem Verfahren hergestellt werden, ist nur durch die robotische Herstellung der Netze beschränkt. Das grosse Potential zur effizienten Herstellung von doppelt gekrümmten Betonbauwerken erklärt, dass wir den Swiss Technology Award 2016 in der Kategorie «Inventors» mit Mesh Mould gewonnen haben.
In der ersten Phase des Projekts wurden die Netze auf der Baustelle vom “in-situ fabricator” Roboter hergestellt. Um die Möglichkeiten und Grenzen von Mesh Mould in einer richtigen Bauumgebung zu testen, haben wir eine 12 m lange, 120 mm dicke doppelt gekrümmte Wand im DFAB HOUSE, einer Residenz die 2019 für Forschungsgäste der EMPA in Dübendorf eröffnet wurde, erstellt.
Folgendes Video zeigen mehr Details zum Bau im DFAB. Wie Sie sehen sieht das Resultat grossartig aus, aber wir haben im grossmassstäblichen Bau einige Aspekte festgestellt die verbessert werden müssen. Zum einen war das Betonieren sehr arbeitsaufwändig. Zum anderen bestand die horizontal Bewehrung aus kleinen, angeschweissten Segmenten: eine ineffiziente Lösung aus Sicht des Tragverhaltens, die nur durch die Fertigung bedingt war.
Mesh Mould Prefabrication: Industrielle Umsetzung
Dank der ergebnisreichen Zusammenarbeit zwischen unserer Gruppe, Gramazio Kohler Research und den Industriepartnern PERI und SIKA, entwickeln wir Mesh Mould weiter um eine Kommerzialisierung zu erreichen. Die Netze werden nun in einer kontrollierten industriellen Umgebung vorgefertigt um die Schwierigkeiten im DFAB HOUSE zu umgehen. Dank eines neuartigen, patentierten, robotergestützten Drahtapplikationsverfahrens ist die Bewehrung jetzt in beide Richtungen durchgehend. Der automatisierte Biege- und Schweissprozess ermöglicht die Herstellung und Schichtung von doppelt gekrümmten Gitterstrukturen aus Bewehrungsstahl mit einem Durchmesser von bis zu 12 mm. Der Prozess beinhaltet die Entwicklung einer wettbewerbsfähigen Betonmischung, die einen robusten Füllprozess auf der Baustelle und eine gute Verdichtung sicherstellt.
Wir führen ein umfangreiches Versuchsprogramm durch, um das Tragverhalten von Mesh Mould Prefabrication zu untersuchen. Dank der Anwendung einer innovativen und automatischen Methode zur Tragwerksbemessung auf Basis des Sandwichmodells, können komplexe Mesh Mould Bauwerke effizient und im Rahmen internationaler Stahlbetonnormen bemessen und optimiert werden. Wir hoffen, mit diesem und ähnlichen Projekten einen Schritt in Richtung einer nachhaltigeren Betonbauweise machen.
Jaime Mata-Falcón
Link to English version: Teaching during the pandemic
Vier Wochen nach Beginn des Frühjahrssemesters 2020, am 16. März, setzte die ETH Zürich den Präsenzunterricht aus. Seit mehr als einem Jahr haben die Studierenden die Hörsäle der ETH nicht mehr betreten. In diesem Blogbeitrag möchte ich einen persönlichen Rückblick auf unsere Lehrtätigkeit in diesem Jahr geben, mit einigen Ideen zu möglichen langfristigen Lehren aus der Pandemie.
Präsenzunterricht eingestellt
Am 13. März 2020 fiel der Entscheid des Bundesrats, alle Hochschulen zu schliessen.Was rückblickend erwartbar wirkt, kam für viele von uns damals überraschend. Auch wenn unsere Schulleitung bereits am Vortag die Einstellung des Präsenzunterrichts beschlossen hatte – wir wurden am 12. März 2020, 21:27 Uhr, durch die Rektorin informiert – mussten wir über ein Wochenende unseren gesamten Unterricht umstellen, u. a. Webcams und Mikrofone beschaffen, eine geeignete Online-Lehrplattform festlegen, Alternativlösungen für die Tafel finden und vieles mehr. Dank des Einsatzes aller Beteiligten konnten wir die damit verbundenen Herausforderungen meistern und am 16. März erfolgreich unsere erste Online-Vorlesung über die Plattform Zoom halten. Seitdem gingen alle Vorlesungen und Kolloquien online über die Bühne, und zwar zur exakt gleichen Zeit, wie wenn sie im Hörsaal stattfänden. Wir halten dies für den besten Weg, die Studierenden dabei zu unterstützen, zumindest einen Teil ihres normalen Studienalltags beizubehalten.
Vorlesungen
Für die Vorlesungen profitierten wir von unserer Lehrplattform concrete.ethz.ch, die wir im Jahr zuvor eingerichtet hatten: Alle Lehrmaterialien waren also für die Studierenden bereits online verfügbar. Naja, nicht wirklich alle: Die Wandtafel konnte natürlich nicht auf die Lehrplattform hochgeladen werden, und einen geeigneten Ersatz für dieses didaktische Werkzeug zu finden, das viele Studierende trotz seiner altmodischen Anmutung den Powerpointfolien vorziehen, war eine große Herausforderung. Im Frühjahrssemester 2020 habe ich zunächst MS Whiteboard verwendet, das meine Schrift zwar krakelig aussehen liess, aber ansonsten anständige Ergebnisse lieferte. Allerdings bereitete der Touchscreen meines Windows-Laptops regelmässig Probleme. Daher wechselten wir zum Herbstsemester, in dem auch Dr. Jaime Mata Falcón unterrichtet, auf ein iPad. Während das Schreiberlebnis des iPads deutlich besser war, war sein Display bei direkter Freigabe unscharf, und wenn es über einen Windows-Laptop gekoppelt war, brach die Verbindung häufig ab. Deshalb verbinden wir das iPad jetzt über ein MacBook. Zudem benutze ich jetzt auch den Lehr-Laptop unserer Gruppe, dessen Touchscreen besser funktioniert als jener meines persönlichen Notebooks. Mit diesem kann ich dadurch als Teilnehmer der Vorlesung beitreten und so überwachen, dass diese korrekt gestreamt wird. Mit all diesen Geräten sieht mein Schreibtisch während der Vorlesungen aus wie derjeinige eines Technik-Nerds, der Geräte für ein Laptop-Magazin testet. Nachdem unser Stream der Vorlesung nun diese Odyssee durchlaufen hat, hat sich ironischerweise die Anzeigequalität von iPads, die direkt in Zoom-Meetings geteilt werden, kürzlich durch ein Software-Update drastisch verbessert…
Die Vorlesung “Bridge Design”, die wir im Frühjahrssemester 2020 zum ersten Mal unterrichteten, beinhaltet einerseits Gastvorträge von renommierten Brückenbauern und andererseits Flipped-Classroom-Übungen. Die Umstellung der Gastvorlesungen auf das Online-Format war bedauerlich, hat aber gut funktioniert. Auch die Flipped-Classroom-Übungen konnten erfolgreich online durchgeführt werden, indem die Studierenden in einem gemeinsamen Meeting auf Breakout-Räume verteilt wurden.

Kolloquien
Neben den Vorlesungen umfassen die Lehrveranstaltungen im Fach Stahlbeton auch Kolloquien, die von Hilfsassistierenden in kleineren Gruppen unterrichtet werden. Dank der Kompetenz und des Einsatzes unserer HilfsassistentInnen ist es uns gelungen, auch diese während des FS2020 nahtlos auf das Online-Format umzustellen. Ein zusätzlicher positiver Aspekt sind die Web-Applikationen, die wir kürzlich im Rahmen eines Innovedum-Projekts entwickelt haben: Diese können von den Studierenden selbständig, aber auch in Vorlesungen und Kolloquien genutzt werden (mehr zu diesen Web-Applikationen und dem gesamten Innovedum-Projekt in einem unserer nächsten Blogs).
Arbeiten von Studierenden
Für die Betreuung der Studierendenprojekte greifen wir im Wesentlichen auf die gleichen Online-Tools zurück wie für die Vorlesungen. Während der ersten Phase der Pandemie, im März und April 2020, waren wir jedoch mit einem Shutdown der gesamten ETH konfrontiert, einschliesslich Büros und Labors. Dies beeinträchtigte mehrere experimentelle Projekte Studierender, die wir auf theoretische Arbeiten umstellen mussten. Dank der Flexibilität und des Einsatzes der Studierenden und ihrer Betreuer konnten alle diese Projekte dennoch erfolgreich abgeschlossen werden. Seit dem Herbstsemester 2020 sind experimentelle Projekte für Studierende wieder möglich.
Prüfungen
Glücklicherweise erlaubte es die Pandemie-Situation zum Zeitpunkt der regulären Prüfungssessionen, unsere schriftlichen Prüfungen in physischer Präsenz abzuhalten. Während dies auch für die mündlichen Prüfungen im Sommer 2020 möglich war, mussten wir diese im Winter 2021 auf ein Online-Format umstellen. Dies war eine weitere Herausforderung, da die Studierenden in unseren Prüfungen Lösungen zu den gestellten Aufgaben skizzieren. Auch dies konnte dank des Einsatzes und der Flexibilität aller Beteiligten erstaunlich gut gemeistert werden. Insgesamt scheinen die Leistungen der Studierenden in den Klausuren während der Pandemie allerdings leicht unter denen der Vorjahre zu liegen. Das kann allerdings auch dadurch bedingt sein, dass im Sommer 2020 im Falle eines Nichtbestehens der Prüfungen kein Fehlversuch angerechnet wurde – normalerweise kann eine Prüfung nur maximal zweimal abgelegt werden. Vielleicht liessen sich einzelne Studierende dazu verlocken, weniger gut vorbereitet zu einer Prüfung anzutreten?
Schluss
Der Übergang vom Präsenz- zum Online-Unterricht verlief sehr gut; sogar viel reibungsloser, als ich es erwartet hatte. Das wäre ohne die leistungsfähigen Online-Konferenz-Tools, die heute zur Verfügung stehen, unmöglich gewesen. So sehr wir uns auch über Softwarefehler beklagen mögen: Kann sich jemand vorstellen, wie die ETH mit dieser Pandemie umgegangen wäre, wenn sich das Virus entschieden hätte, 20 Jahre früher aufzutauchen?
In der Tat haben Online-Vorlesungen ihre Vorteile. Sie können im eigenen Tempo angeschaut werden. Unklare oder schwierige Passagen können nachgespielt und langweilige übersprungen werden – ich hoffe allerdings, unsere Studierenden benötigen letztere Funktion nicht allzu oft. Aufgezeichnete Vorlesungen den Studierenden zur Verfügung zu stellen, ist also auch nach der Rückkehr in die Präsenzlehre eine Überlegung wert. Zudem ist es viel einfacher, Gastvorträge von namhaften Referenten aus dem Ausland zu organisieren, wenn diese nicht anreisen müssen. Was Letzteres betrifft, so hat uns die Pandemie auch gelehrt, dass physische Anwesenheit nicht immer notwendig ist. Ich bin überzeugt, dass wir nach der Pandemie weniger reisen und damit effizienter sein werden, und gleichzeitig die Umwelt weniger belasten.
Allerdings können Online-Meetings die physische Anwesenheit nicht vollständig ersetzen. Dies gilt nicht nur für Aktivitäten wie Exkursionen oder experimentelle Arbeiten, sondern genauso für Aufgaben, die grundsätzlich durchaus remote durchgeführt werden können. Zum Beispiel können Online-Projektpräsentationen den Studierenden nicht die Erfahrung bieten, persönlich vor einem Publikum zu präsentieren. Ebenso vermisse ich das Feedback der Studierenden in meinen Online-Vorlesungen sehr – auch wenn dieses, abgesehen von einigen Fragen in den Pausen, meist nonverbal war. Und wenn ich an mein eigenes Leben als Studierender zurückdenke, dann gibt es nicht viel, was ich lieber “online” gemacht hätte.

Heute ist nicht klar, wie lange wir wegen der Pandemie noch aus der Ferne unterrichten müssen. Nur zur Erinnerung: Der Masterplan unserer Schulleitung vom 15. April 2020 sah eine Rückkehr zum Normalbetrieb bis zum Herbstsemester 2020 vor (was viele pessimistisch fanden). Dennoch hoffe ich, dass wir spätestens ein Jahr nach diesem Termin, also im Herbstsemester 2021, zum Präsenzunterricht zurückkehren können. Wann auch immer es soweit sein wird, ich freue mich schon jetzt darauf.
Walter Kaufmann
Der Titel dieses Blogeintrags ist die komprimiert möglichste Beschreibung dessen, was mich in den letzten fünf Jahren beschäftigt hat. Im vergangenen Dezember habe ich meine Dissertation zu diesem Thema erfolgreich verteidigt, die ich unter der Leitung von Prof. Dr. W. Kaufmann erarbeitet habe. In diesem Beitrag werde ich versuchen, Ihnen eine etwas weniger komprimierte Version des Inhalts der Arbeit zu geben, indem ich Antworten auf die folgenden Fragen gebe.
Was ist das Problem und warum ist es relevant?
Der Grund dafür, dass wir im Jahr 2021 immer noch über einen Lastfall diskutieren, für den es Normenvorschriften gibt, hängt mit der Tatsache zusammen, dass die entwickelten Länder heute mit der Herausforderung einer alternden Infrastruktur konfrontiert sind. Um ihre Tragsicherheit zu gewährleisten, müssen viele Infrastrukturobjekte neu überprüft werden, da sowohl die Verkehrsintensität als auch die Verkehrslasten seit ihrer Errichtung zugenommen haben. Die aktuellen Bemessungsvorschriften und -richtlinien beruhen auf früheren Untersuchungen und deren zugehörigen Modellen, die mit dem Ziel konzipiert wurden, neue Bauwerke sicher zu bemessen. Sie sind daher konservativ und enthalten Reserven. Das Vorsehen gewisser Traglastreserven ist beim Entwurf neuer Bauwerke sicherlich angebracht ist, da es in der Regel mit einer Erhöhung der Robustheit und Redundanz bei geringen zusätzlichen Kosten einhergeht. Dies gilt indes nicht für bestehende Tragwerke.
Wie im Titel angedeutet, ist einer der zu beurteilenden Lastfälle die Kombination von Längsschub und Querbiegung. Es ist klar, dass die Belastung eines Brückenträgers Längsbiegung und damit Längsschub – also eine Beanspruchung durch in der Ebene des Stegs wirkende Kräfte – verursacht. Gleichzeitig müssen die auf die Fahrbahn aufgebrachten Lasten aber auch in Querrichtung abgetragen und in den Längsträger eingeleitet werden, was zu einer Biegebeanspruchung im Querschnitt führt. Da der Steg monolithisch mit der Fahrbahnplatte verbunden ist, nimmt er einen grossen Teil des Biegemoments auf, das er zusätzlich zu den in der Ebene wirkenden Schubkräften aufnehmen muss.

Welche Modelle gibt es, und warum war zusätzliche Forschung notwendig?
Eine Gruppe von Ansätzen, die als starr-ideal plastische Modelle klassifiziert werden können, machen sich zunutze, dass Krümmungen um die Vertikalachse und/oder Verdrillungen des Stegelements durch die Fahrbahnplatte, die untere Kastenplatte und benachbarte Stegelemente, sowie zusätzlich durch allfällige Querscheiben oder -träger behindert werden. Anstelle der zugehörigen sogenannten verallgemeinerten Spannungen des Stegelements treten somit verallgemeinerte Reaktionen auf, die einen beliebigen Wert annehmen, der den Tragwiderstand in Funktion der verbleibenden verallgemeinerten Spannungen maximiert.

Die Tatsache, dass das Drillmoment und das Biegemoment um die vertikale Achse beliebige Werte annehmen können, ermöglicht eine seitliche Verschiebung des Druckfeldes, das für die Übertragung des Längsschubes verantwortlich ist, zur Biegedruckseite. Dadurch können die Bügel auf der Biegezugseite fast vollständig für die Übertragung des Biegemoments genutzt werden, was zu einer deutlichen Erhöhung des Tragwiderstands führt.
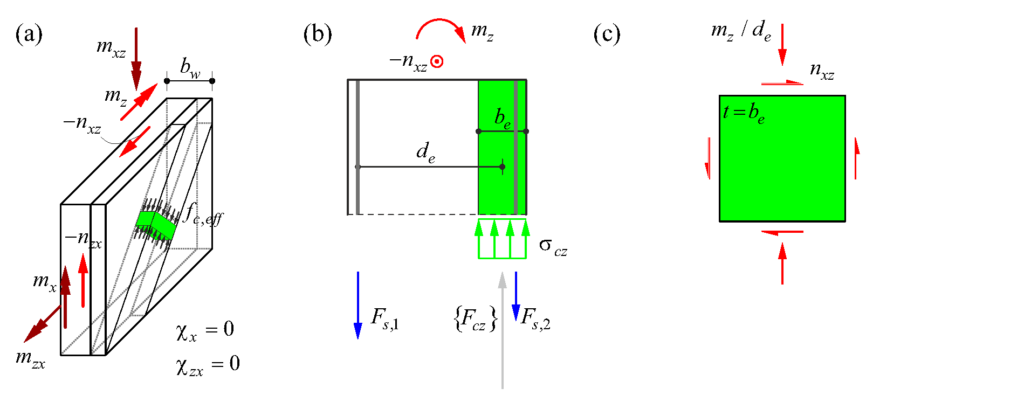
Diese starr-ideal plastischen Modelle haben das Potenzial, gute Abschätzungen der Tragfähigkeit des Stegs zu liefern. Ihre Anwendbarkeit auf Bauteile mit sehr geringem Bügelbewehrungsgehalt ist jedoch eingeschränkt, da die ihnen zugrunde liegende Annahme eines ausreichenden Verformungsvermögens in diesen Fällen ohne expliziten Nachweis nicht erfüllt ist.
Darüber hinaus wurden diese Modelle anhand einer sehr begrenzten Anzahl von Versuchen validiert. Infolgedessen wurde die zweite grundlegende Annahme, nämlich dass eine seitliche Verschiebung des Druckfeldes durch die kinematischen Randbedingungen des Stegs ermöglicht wird, nie experimentell verifiziert.
Weiter gilt es die Tatsache zu beachten, dass die Querbiegemomente im Steg nicht a priori bekannt sind, sondern von der Steifigkeit des Stegs relativ zur Fahrbahnplatte abhängen. Auch dieser Effekt ist bisher weder theoretisch noch experimentell untersucht worden. Wenn der Steg ein ausreichendes Verformungsvermögen aufweist (d.h. nicht vorzeitig versagt, sondern allmählich seine Biegesteifigkeit verliert), können Querbiegemomente aus exzentrischen Verkehrslasten vom Steg zur Fahrbahnplatte umgelagert und Querbiegemomente aus der Verformung des Querschnitts reduziert werden (einhergehend mit einer Zunahme der Wölbtorsion).
Wie wurden die Wissenslücken geschlossen?
Die Wissenslücken wurden durch die Durchführung von Grossversuchen im Large Universal Shell Element Tester an ebenen Schalenelementen, die isolierte Stegelemente einer Hohlkastenbrücke darstellten, geschlossen. Der Large Universal Shell Element Tester ist eine Versuchseinrichtung, die von zwei Testanlagen an der Universität Toronto inspiriert ist, und deren Fähigkeiten kombiniert. Er ermöglicht die Durchführung von Grossversuchen an Stahlbetonschalenelementen mit Abmessungen von 2 m x 2 m und einer variablen Dicke. Der Aufbau erlaubt das Aufbringen kontrollierter, beliebiger Lastkombinationen an den vier Rändern des Versuchskörpers (8 unabhängige Spannungsresultierende oder aufgezwungene Verformungen) mit Hilfe von 100 hydraulischen Pressen (siehe Kaufmann et al. 2019 and LUSET).
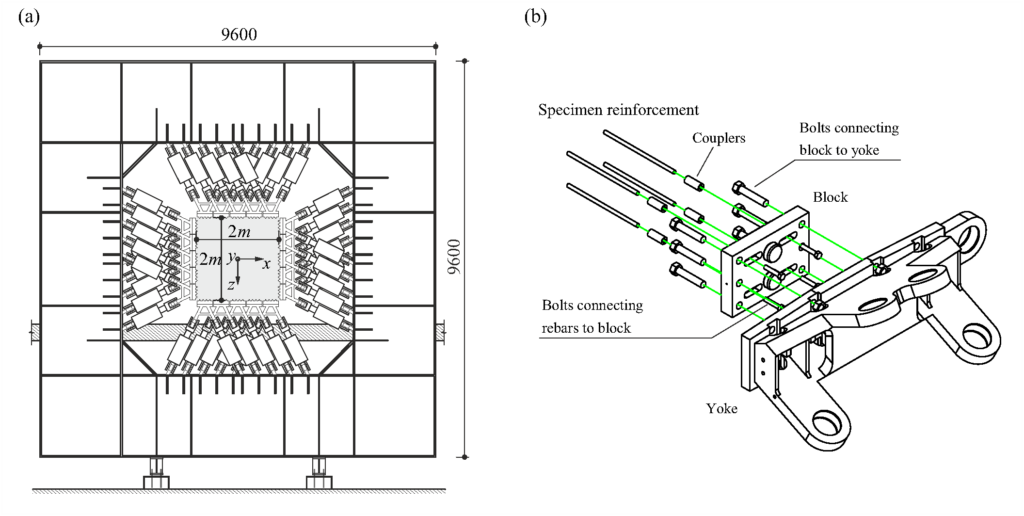
Es wurden insgesamt 10 Versuche an orthogonal bewehrten Stahlbetonschalenelementen durchgeführt. Die Prüfkörper, die einen Teil eines Hohlkastenstegs darstellten, wurden verschiedenen Kombinationen aus homogener Belastung und aufgezwungenen Verformungen unterworfen. Diese Lastkombinationen waren so definiert, dass die dem Steg durch die gesamte Brückenkonstruktion vorgegebenen Randbedingungen angemessen berücksichtigt wurden. Zu den untersuchten Parametern gehörten der Bewehrungsgehalt, die kinematischen Restriktionen und die Belastungsreihenfolge. Um die Auswirkung der Steifigkeitsabnahme des Stegs auf die Querbiegemomentenverteilung zu untersuchen, wurde auch ein sogenannter Hybridversuch durchgeführt. Bei diesem Test bildete ein Finite-Elemente-Modell, das kontinuierlich mit der tatsächlichen Biegesteifigkeit des physischen Prüfkörpers aktualisiert wurde, das globale Verhalten des Brückenquerschnitts ab, und beeinflusste dementsprechend die aufzubringende Last.

Was waren die wichtigsten experimentellen Ergebnisse?
Die Ergebnisse der Versuchsreihe bestätigten die Annahme der meisten existierenden starr-ideal plastischen Modelle, dass sich das für die Übertragung der Querkraft in Längsrichtung wirksame Druckfeld tatsächlich seitlich in Richtung der Biegedruckseite des Stegs verschiebt. Die auf das verschobene Druckfeld einwirkende Biegedruckkraft wirkt sich, zusammen mit den insgesamt auf den Steg einwirkenden verallgemeinerten Reaktionen, günstig auf dien Tragwiderstand des Steges unter kombinierter Beanspruchung aus. Die massgebende Versagensart bei Elementen mit sehr geringem Bügelbewehrungsgehalt war in allen Versuchen das Reissen der Bügelbewehrung. Dieser spröde Versagensmodus, der vor einer signifikanten Ausnutzung des Betons auf Druck eintrat, schränkt die Anwendbarkeit von Modellen ein, die nicht explizit das Verformungsvermögen überprüfen. Die experimentellen Ergebnisse unterstreichen damit die Bedeutung des Vergleichs von Verformungsbedarf und Verformungsvermögen bei der Beurteilung von Bauteilen mit sehr niedrigem Bügelbewehrungsgehalt.
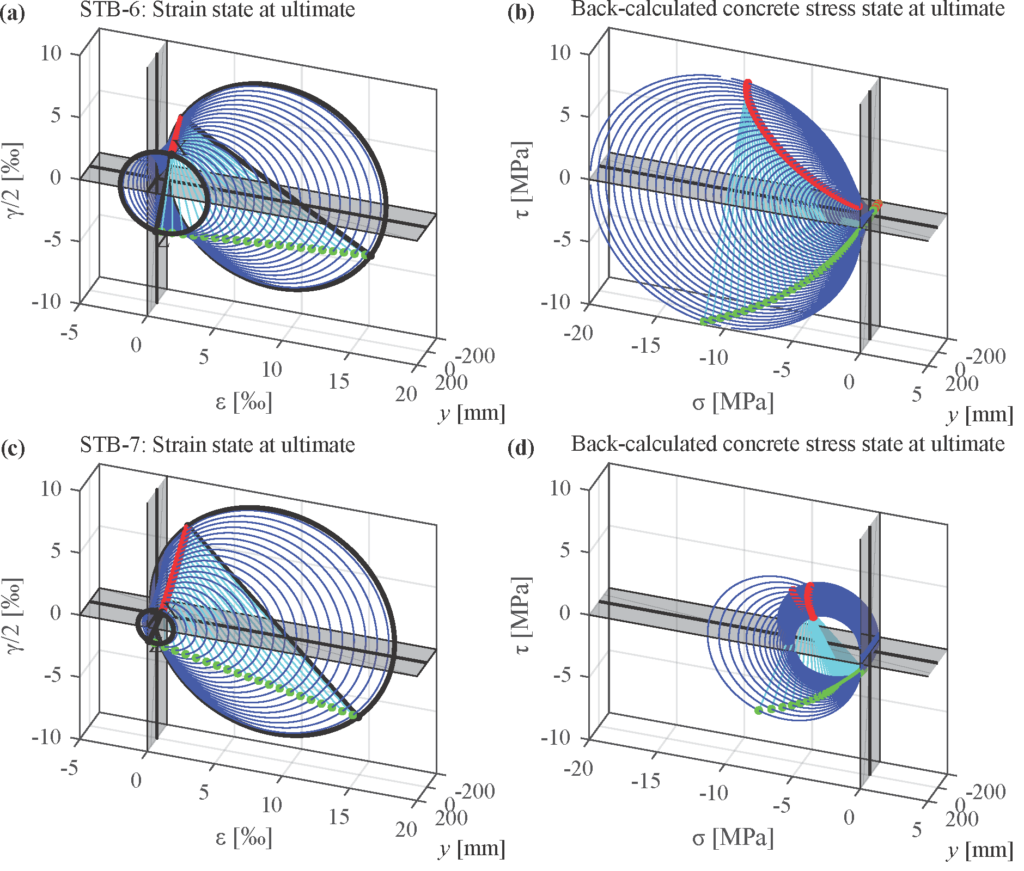
Der durchgeführte Hybridversuch, der das Systemverhalten berücksichtigte, bestätigte den günstigen Einfluss einer Umlagerung der Biegemomente in einem Kastenträger auf den Tragwiderstand des Stegs bei kombinierter Längsschub- und Querbiegebeanspruchung. Diese Aussage gilt jedoch unter der der Voraussetzung, dass alle angrenzenden Bauteile (die Fahrbahnplatte und die untere Kastenplatte) eine ausreichende Tragreserve aufweisen, um die dadurch resultierende, zusätzliche Belastung aufnehmen zu können. Durch die Berücksichtigung des Systemverhaltens bei der Beurteilung bestehender Brücken kann daher der Umfang der erforderlichen Verstärkungsmassnahmen allenfalls reduziert werden. Falls Verstärkungsmassnahmen dennoch als notwendig erachtet werden, ist eine Erhöhung der Steifigkeit der Fahrbahnplatte anderen, deutlich aufwändigeren Verstärkungsmassnahmen vorzuziehen.
Wie können bestehende Methoden um eine Überprüfung des Verformungsvermögens erweitert werden (unter Beibehaltung ihrer Einfachheit)?
Die Erweiterung bestehender Modelle zum Nachweis des Verformungsvermögens erfordert die Berücksichtigung komplizierterer Ansätze zur Modellierung des Verhaltens von Beton und Bewehrung (insbesondere Druckentfestigung und Zugversteifung). Dies führt dazu, dass ihre Formulierungen stark nichtlinear werden und daher komplexe iterative Algorithmen zur Lösung erforderlich sind. Um ein vereinfachtes Verfahren zur Bestimmung des Tragwiderstands zu erhalten und gleichzeitig die Grenzen des Verformungsvermögens zu berücksichtigen, wurde ein grafischer Ansatz entwickelt. Dieser nutzt die in den Versuchen beobachtete Tatsache, dass Stege mit sehr kleinem Bügelbewehrungsgehalt infolge Reissen der Bügel versagen, um das Problem auf zwei kinematische Unbekannte zu reduzieren. Man erhält eine Abschätzung des Querbiegewiderstands und der zugehörigen Verformung, indem der Schnittpunkt des Lösungsraums mit den Zielwerten für die aufgebrachte Längsschubbeanspruchung grafisch bestimmt wird. Neben der Ermittlung der Bruchlast kann die Methode auch für die Untersuchung des Systemverhaltens verwendet werden, da sie die Berechnung vereinfachter bilinearer Momenten-Krümmungs-Diagramme des Stegs bei gegebenem Längsschub ermöglicht.
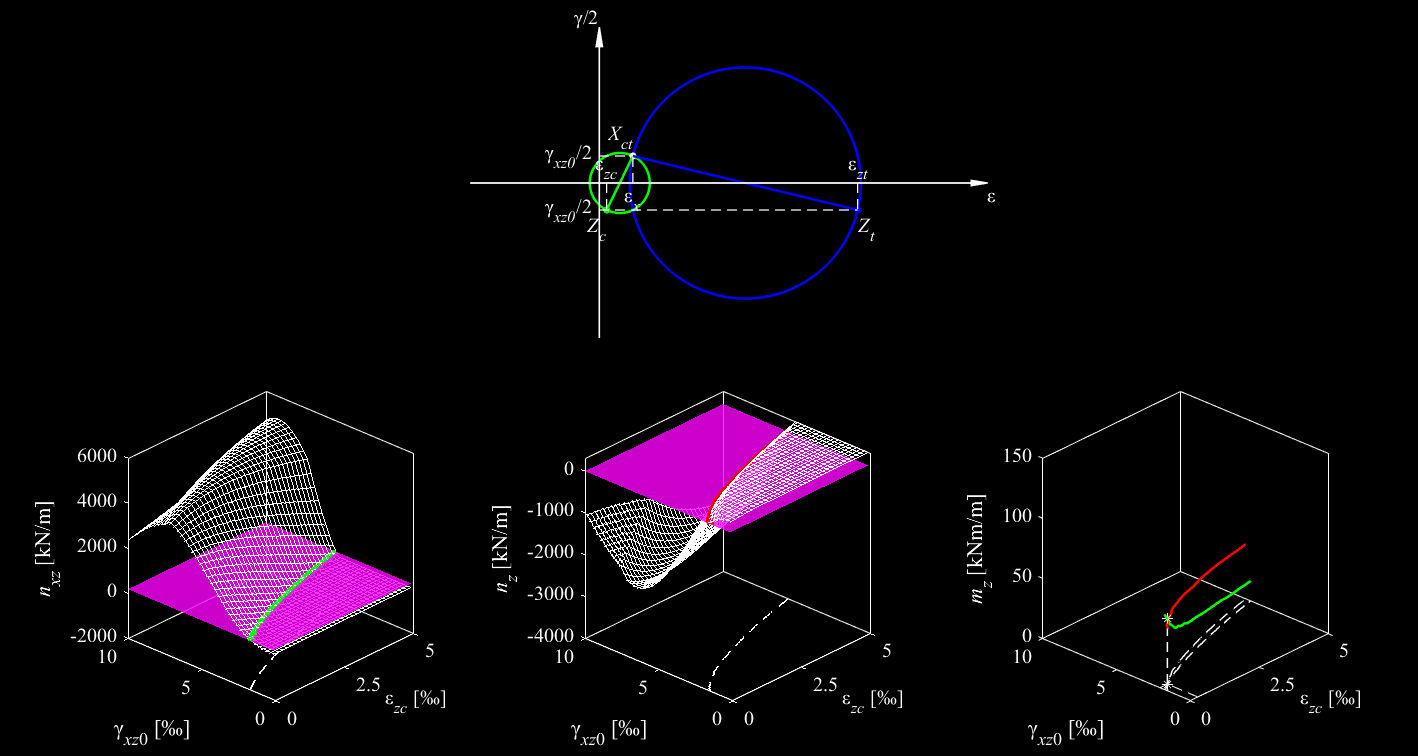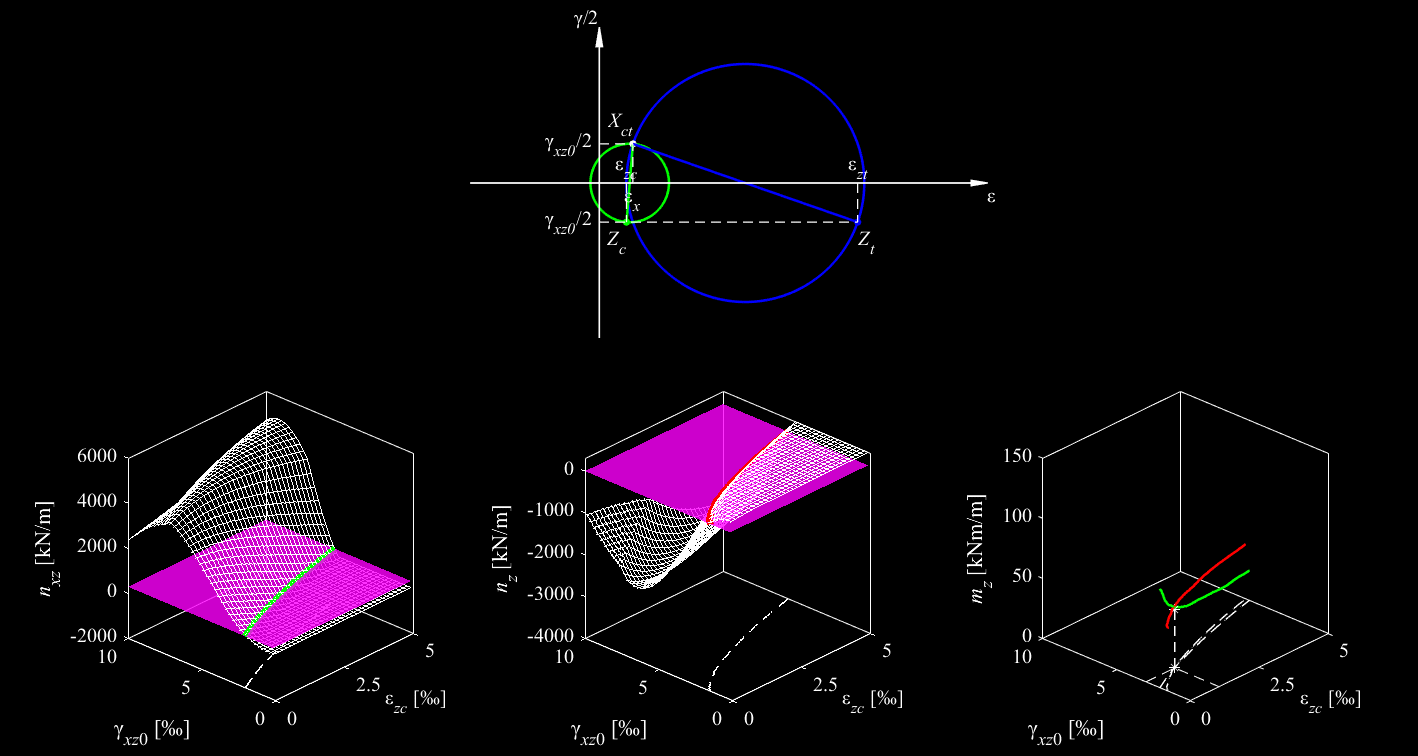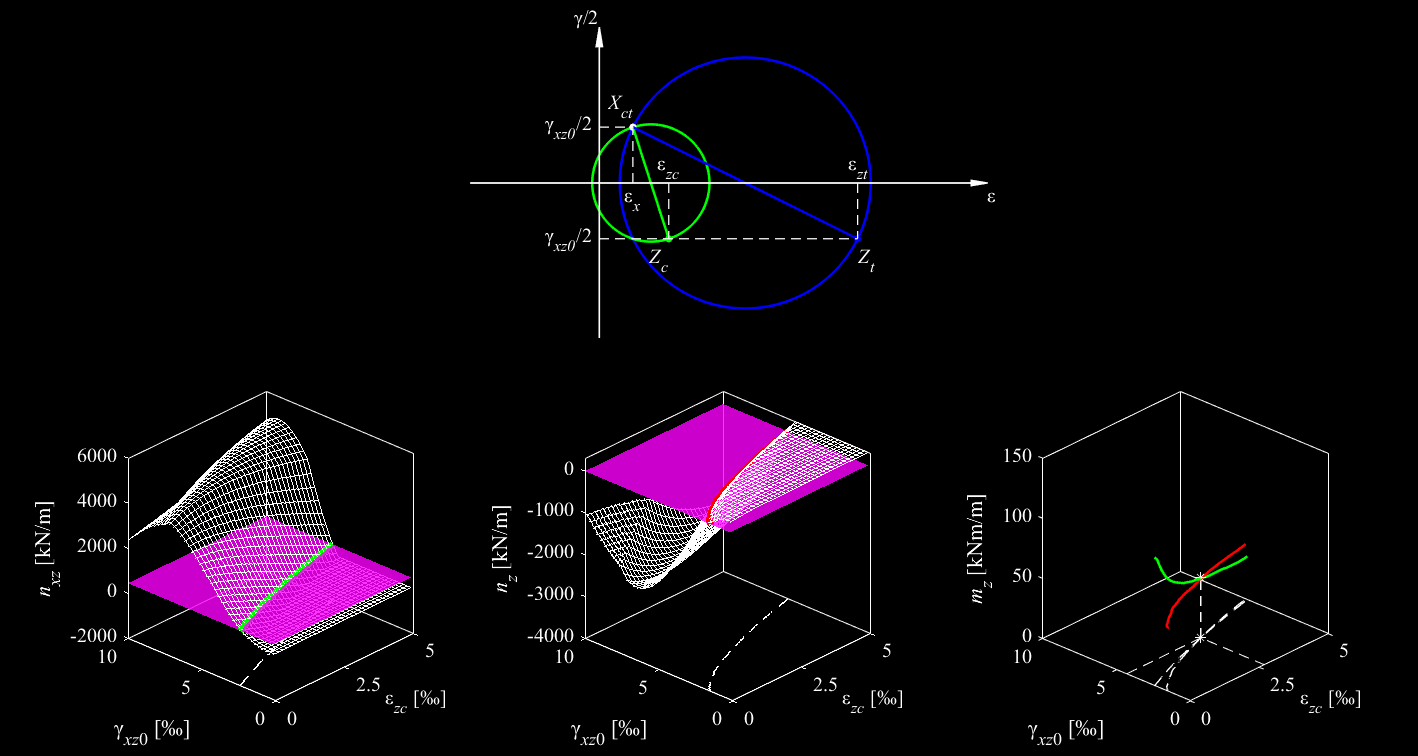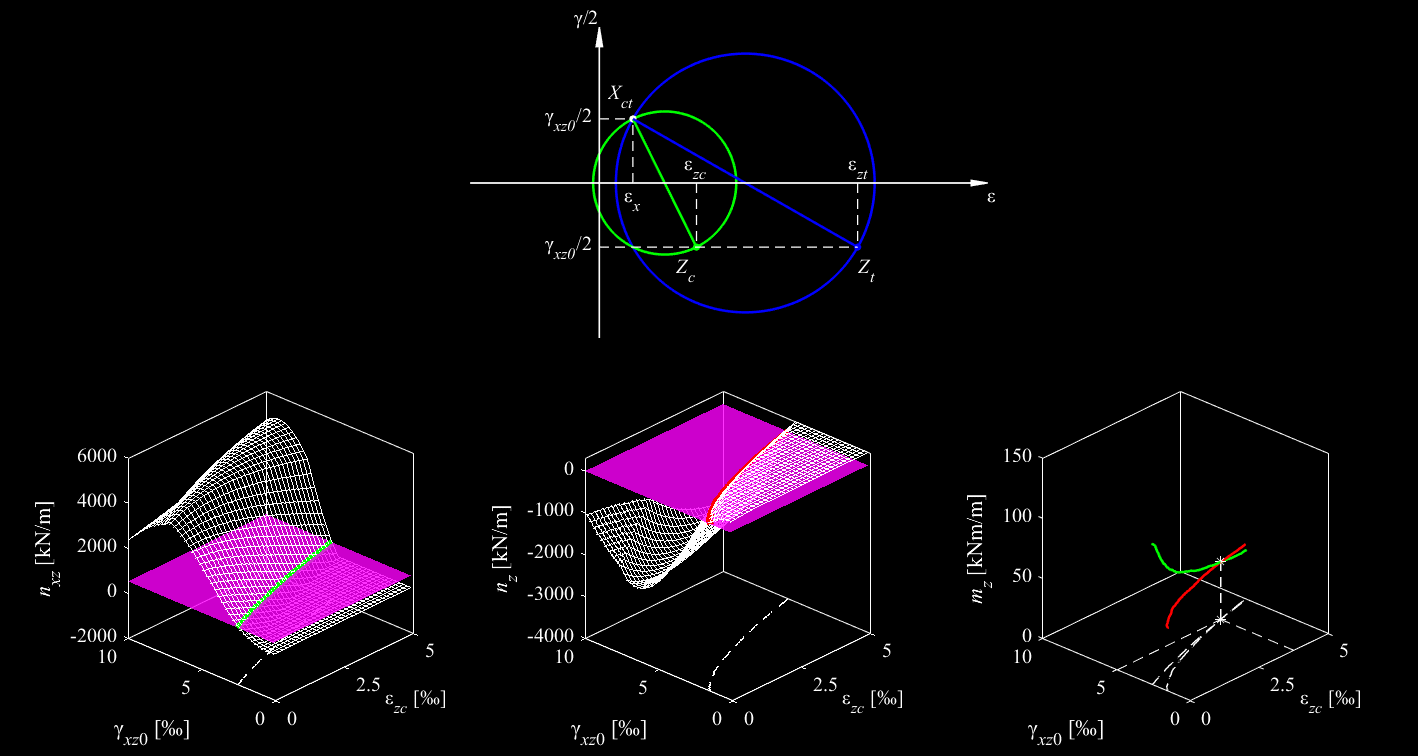
Was ist die wichtigste Erkenntnis für Ingenieure in der Praxis?
Bei der Überprüfung bestehender Tragwerke wird sehr viel Wert auf die maximale Ausnutzung der vorhandenen Tragwiderstands gelegt. Im Falle einer kombinierten Beanspruchung von Längsschub und Querbiegung ist es zur Vermeidung unnötiger Verstärkungsmassnahmen jedoch in vielen Fällen erfolgversprechender, das auf den Steg wirkende Querbiegemoment möglichst realistisch abzuschätzen. Dies gilt insbesondere verglichen mit der maximalen Ausnutzung vorhandener Traglastreserven ohne Berücksichtigung einer Lastumlagerung. Daher wird eine detailliertere Untersuchung des Systemverhaltens unter Berücksichtigung der Steifigkeitsabnahme im Steg bei zunehmender Belastung empfohlen.
Link to English version: Are truss models outdated in the 21st century?
Wer wie ich an der ETH studiert hat, kennt die Antwort auf die Frage, welche der Titel des Blogeintrags aufwirft: Generationen von Bauingenieuren und Bauingenieurinnen eigneten sich nicht grundlos Wissen über Fachwerkmodelle und Spannungsfelder an, und auch heute noch sind sie, als wertvolle Instrumente für die Bemessung im Betonbau, in meinen Vorlesungen von zentraler Bedeutung. Vielleicht interessiert es Sie aber, weshalb ich es keineswegs als selbstverständlich erachte, dass Fachwerkmodelle auch in Zukunft verwendet werden – und was wir unternommen haben, um dem Aussterben dieser Methoden entgegenzuwirken?
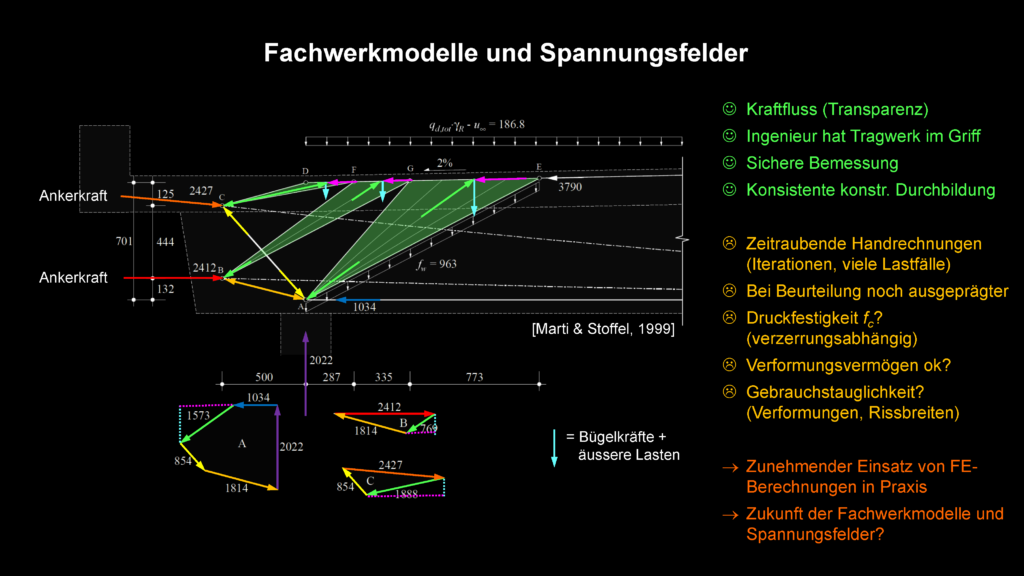
Die Ursprünge von Fachwerkmodellen reichen bis in die Anfangszeit des Betonbaus zurück. Auf eine konsistente mechanische Grundlage gestellt und für die Bemessung verwendet wurden sie allerdings erst viel später: In der zweiten Hälfte des 20. Jahrhunderts wagten es einige Pioniere, darunter Professor Thürlimann und seine Mitarbeiter an der ETH Zürich, Traglastverfahren auf Stahlbeton anzuwenden. Sie interpretierten dazu Fachwerkmodelle als diskontinuierliche Spannungsfelder, und diese wiederum als Lösungen nach dem unteren Grenzwertsatz der Plastizitätstheorie. Fachwerkmodelle liefern somit konservative Resultate und ermöglichen es, Zwangsbeanspruchungen zu vernachlässigen – was sie zum perfekten Instrument für die Bemessung im Grenzzustand der Tragsicherheit macht.
So selbstverständlich dies zumindest den ETH-Alumni unter uns erscheinen mag, war es das damals keineswegs. Vielmehr stiess die neue Theorie anfänglich selbst innerhalb der ETH Zürich auf heftigen Widerstand (siehe beispielsweise Basler 1983). In der Tat ist die Duktilität der Bewehrung, und vor allem diejenige des Betons, natürlich begrenzt. Durch die Vernachlässigung der Zugfestigkeit des Betons, das Vorsehen einer Mindestbewehrung und die Anwendung vorsichtiger Werte für die Betondruckfestigkeit kann jedoch ein duktiles Verhalten gewährleistet und damit die Voraussetzung für die Anwendung der Plastizitätstheorie geschaffen werden. Diese konstruktiven Regeln einzuhalten ist bekanntlich generell ratsam. Andernfalls wird die Bemessung semi-empirisch und damit um Grössenordnungen komplizierter.
Zurück zu den Fachwerkmodellen: Sie bilden, wie bereits gesagt, eine konsistente Grundlage für die sichere Bemessung von Betonbauten, und sie ermöglichen in vielen Fällen eine direkte Bemessung der Bewehrung für eine gegebene Beanspruchung. Der Kraftfluss kann verfolgt werden und die Berechnungen sind transparent und nachvollziehbar. Vor allem aber hat der Ingenieur resp. die Ingenieurin die Kontrolle über die Bemessung und kann beispielsweise ein praxistaugliches Bewehrungslayout wählen. All dies sind klare Vorteile bei einer Anwendung in der Bemessungspraxis.
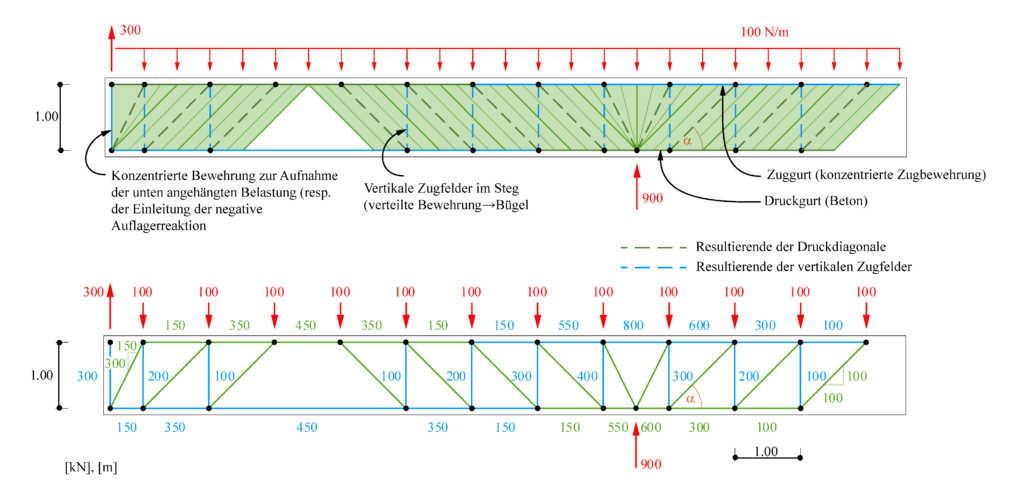
Fachwerkmodelle haben aber auch Nachteile. Da ihre Geometrie meist iterativ angepasst werden muss und verschiedene Laststellungen zu untersuchen sind, ist die Anwendung als Handrechnung in der Praxis oft aufwändig. Zudem eignen sie sich nicht direkt für die Ermittlung von Durchbiegungen und Rissbreiten im Gebrauchszustand, wofür weitere Modelle herangezogen werden müssen, und die in modernen Normen stipulierte Abhängigkeit der Druckfestigkeit des Betons vom Verzerrungszustand erschwert die händische Entwicklung von Fachwerkmodellen enorm.
Daher besteht in der Praxis eine klare Tendenz, für die Tragwerksanalyse und Bemessung eines der heute verfügbaren, benutzerfreundlichen Computerprogramme auf Basis der Methode der finiten Elemente (FE) einzusetzen, welches für die Grenzzustände der Tragsicherheit und Gebrauchstauglichkeit verwendet werden kann – was zwar oft unpraktische und unwirtschaftliche Bewehrungen ergibt, aber automatisierbar und damit bei der Bemessung sehr effizient ist.
Dies gilt für händisch entwickelte Fachwerkmodelle und Spannungsfelder leider nicht. Wenn diese Schwächen nicht beseitigt werden, besteht die reale Gefahr, dass sie bald nur noch im Hörsaal eingesetzt werden – und vielleicht noch als anschauliches Hilfsmittel für die Formfindung und das Verfolgen des Kraftflusses im konzeptionellen Entwurf. Dies war mir bereits bewusst, als ich noch in der Praxis tätig war, und ich wusste auch schon, wie man dieser Entwicklung entgegenwirken kann, hatte doch mein Vorgänger bereits vor über 30 Jahren die Lösung vorgeschlagen (siehe Zitat): Fachwerkmodelle müssen in benutzerfreundliche Computerprogramme implementiert werden, ohne dabei ihre Vorteile – Transparenz und Kontrolle über die Bemessung – zu beeinträchtigen.
Recent advances in computer development indicate that there might be much better ways of using the unique capabilities of computers to assist reinforced concrete designers in the future. There is a considerable potential for applying interactive computer programs with graphical input and output that could replace the traditional drawing board and pocket calculator methods for developing truss models. Apart from ultimate strength considerations, such programs would allow us to investigate the deformations in the cracked state by taking appropriate truss member stiffnesses into account.
Peter Marti: “Truss Models in Detailing,” Concrete International, Vol. 7, No. 12, Dec. 1985, pp. 66-73
Die Zeit war aber noch lange nicht reif für eine Umsetzung dieser visionären Idee. Erste Programme für ideal plastische Spannungsfelder (u.a. Hajdin 1990) waren wenig benutzerfreundlich. Weder diese, noch die kurze Zeit später entwickelten Programme zur plastischen Bemessung auf Basis linear elastischer FE-Analysen (u.a. Despot 1995) waren in der Lage den Gebrauchszustand oder das Verformungsvermögen zu untersuchen.
Auch als Anfang des 21. Jahrhunderts erste Programme für die automatisierte Stahlbetonbemessung mit Fachwerkmodellen entwickelt wurden, setzten sich diese in der Praxis nicht durch. Diese diskontinuierlichen Modelle scheiterten an der automatisierten, zuverlässigen Bestimmung von Betondruckfestigkeit und Steifigkeiten.
Das an der EPFL entwickelte Programm EPSF zeigte aber, dass die Verwendung kontinuierlicher Spannungsfelder dies bedeutend vereinfacht (siehe Fernández Ruiz und Muttoni 2007). Im Wesentlichen ist EPSF eine vereinfachte FE-Berechnung. Das Programm ist frei verfügbar, setzt jedoch Java-Script Kenntnisse voraus und ist für Untersuchungen des Gebrauchszustands und der Duktilität nur bedingt geeignet, da die Zugversteifung vernachlässigt und linear elastisch-ideal plastisches Materialverhalten vorausgesetzt wird.
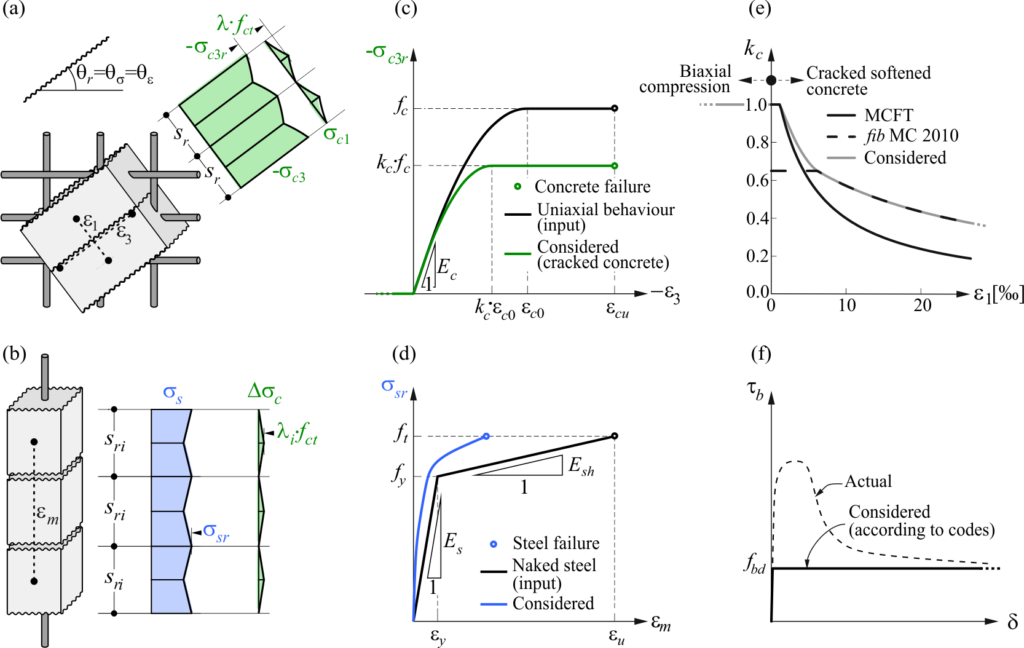
Eigentlich ist die Implementierung realitätsnäherer Stoffgesetze aber leicht umsetzbar, und insbesondere das von Viktor Sigrist und Manuel Alvarez entwickelte Zuggurtmodell (Marti et al. 1998) eignet sich dafür hervorragend. Einerseits wird damit die Mitwirkung des Betons zwischen den Rissen mechanisch konsistent erfasst, andererseits ist der Tragwiderstand unabhängig von der Zugfestigkeit des Betons, womit die Verbindung zu plastischen Bemessungsverfahren gewährleistet bleibt.
Als mich kurz nach meiner Rückkehr an die ETH Zürich die Tschechische Software-Firma IDEA StatiCa kontaktierte, um gemeinsam «ein Tool für automatisierte Fachwerkmodelle» zu entwickeln, schlug ich daher genau dies vor: Kontinuierliche Spannungsfelder mit dem Zuggurtmodell zu verknüpfen. In der Zwischenzeit ist daraus die Compatible Stress Field Method (CSFM) entstanden, und das darauf basierende Programm IDEA StatiCa Detail. Dieses ist weltweit erhältlich, auch in der Schweiz (https://www.ingware.ch/produkte/statik-und-dynamik/idea-statica-detail/idea-statica-detail.html).
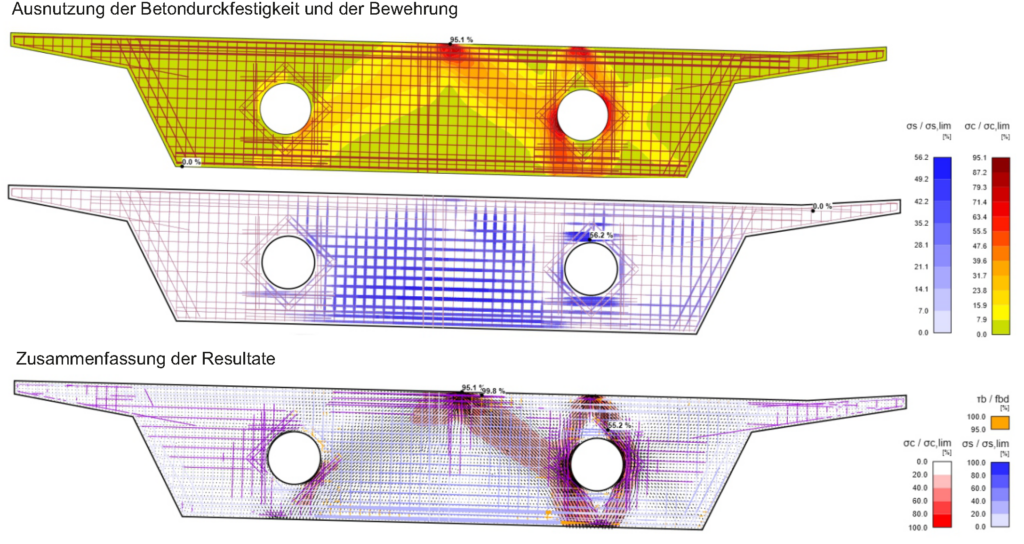
Als kommerzielle Software ist IDEA StatiCa Detail (nach Ablauf der kostenlosen Testlizenz) zwar nicht gratis, dafür aber sehr benutzerfreundlich und leistungsfähig. Die Grundprinzipien und die Ergebnisse seiner Validierung an zahlreichen Beispielen sind in einem Verification Book zusammengestellt, und ich habe das Programm kürzlich – mit einem etwas ausführlicheren geschichtlichen Rückblick auf die Entwicklung von Spannungsfeldern und einigen Anwendungsbeispielen – an einer Schulung vorgestellt (hier geht’s zum Youtube-Video).
Weder ich persönlich noch die ETH Zürich haben übrigens ein finanzielles Interesse am Vertrieb von IDEA StatiCa Detail. Unser Vorteil ist immaterieller Art: Wir hoffen, damit einen Beitrag zum Erhalt der gefährdeten Spezies der Fachwerkmodelle und Spannungsfelder zu leisten. Egal, ob sie dieses Anliegen teilen oder einfach ein effizientes Tool für die Bemessung von Stahlbetontragwerken mit Spannungsfeldern suchen: Es würde uns freuen, wenn Sie das Programm bei Gelegenheit einmal ausprobieren.
Walter Kaufmann
Link to English version: Bridging university and industry in structural engineering
Sind Sie in der Praxis tätig und an neuen Entwicklungen im konstruktiven Ingenieurbau an der ETH Zürich interessiert? Schliessen Sie ein Bachelorstudium im Bauingenieurwesen ab und ziehen eine Vertiefung in Konstruktion an unserem Departement in Betracht? Oder möchten Sie nach dem Masterstudium ein Doktorat in einem unserer Forschungsgebiete in Angriff nehmen? Oder haben Sie diesen Blog aus anderen Gründen gefunden? Warum auch immer Sie diese Zeilen lesen: Willkommen im neuen Blog der Professur für Betontragwerke und Brückenbau an der ETH Zürich!
In naher Zukunft werden Sie hier Beiträge zu verschiedenen Themen finden, wie z. B. aktuelle Erkenntnisse und Publikationen, Aktivitäten in Kommissionen, laufende Versuche in unserem Labor oder Rückblicke auf Prüfungen. Ausserdem werden wir unsere Gedanken und Meinungen zu aktuellen und relevanten Themen teilen.

In diesem einleitenden Beitrag möchte ich Ihnen unsere Hauptaktivitäten vorstellen und erklären, warum wir es als notwendig erachten, diesen Blog zu starten. Tatsächlich wurde mir Letzteres erst vor kurzem klar: Als ich 2014 an die ETH Zürich zurückkehrte, nachdem ich mehr als 15 Jahre lang als Bauingenieur gearbeitet hatte, war ich sehr gut in der Praxis vernetzt. Ich hielt diese Verbindungen für selbstverständlich und hätte mir nicht im Traum vorgestellt, Social-Media-Aktivitäten zu starten, um den Austausch mit Fachleuten zu fördern. Im Laufe der letzten Jahre wurde mir jedoch zunehmend bewusst, dass meine ehemaligen Kollegen keine – oder höchstens eine sehr vage und oft falsche – Vorstellung von unseren Aktivitäten in Forschung und Lehre hatten.
Vor einiger Zeit sagte mir ein guter Freund und sehr kompetenter Bauingenieur unverblümt, dass er und die meisten Ingenieure in der Industrie keine Ahnung hätten, was “auf dem Hönggerberg” (für Nicht-ETH-Absolventen: Das ist der Ort, an dem wir uns befinden) los sei. Ich fragte dann meine Gruppenmitglieder, ob sie ähnliche Rückmeldungen von ihren in der Praxis tätigen Kollegen erhalten hätten, was sie bestätigten. Wir begannen dann, über Möglichkeiten zu diskutieren, diese Situation zu verbessern, und schliesslich wurde die Idee dieses Blogs geboren.
Aber was sind denn überhaupt diese Aktivitäten unserer Gruppe, über die wir Sie informieren wollen? Im Wesentlichen sind es drei Bereiche:
Lehre, Forschung und Dienstleistung
Persönlich betrachte ich die Lehre als meine wichtigste Aufgabe, auch wenn die akademische Reputation eines ETH-Professors in erster Linie von den Leistungen in der Forschung abhängt. Genau genommen ist die Lehre an der ETH keine Pflicht, sondern ein Vergnügen: Die Möglichkeit, begabte, motivierte junge Menschen zu unterrichten, ist ein Privileg und eine der erfüllendsten Aufgaben, die man sich vorstellen kann.
Laut der jährlichen Lehrevaluation durch die Studierenden gehören unsere Kurse zu den anspruchsvollsten des Departements, was kein Zufall ist: Ich bin davon überzeugt, dass die Studierenden lieber herausgefordert werden, als sich zu langweilen (was übrigens ebenfalls durch die Ergebnisse der Evaluation bestätigt wird). Wir bemühen uns, kritisches Denken und selbstmotiviertes Lernen zu fördern, was in der heutigen Zeit, wo Kreditpunkte die Währung der höheren Bildung sind, nicht immer einfach ist.
Ausführlichere Informationen darüber, wie wir dies zu erreichen versuchen, und über unseren Unterricht im Allgemeinen, folgen in den nächsten Beiträgen. Wenn Sie in der Zwischenzeit neugierig geworden sind, laden wir Sie ein, einen Blick auf unsere E-Learning-Plattform https://concrete.ethz.ch/ zu werfen. Vielleicht möchten Sie sogar die interaktiven Apps https://concrete.ethz.ch/applikationen/ ausprobieren?
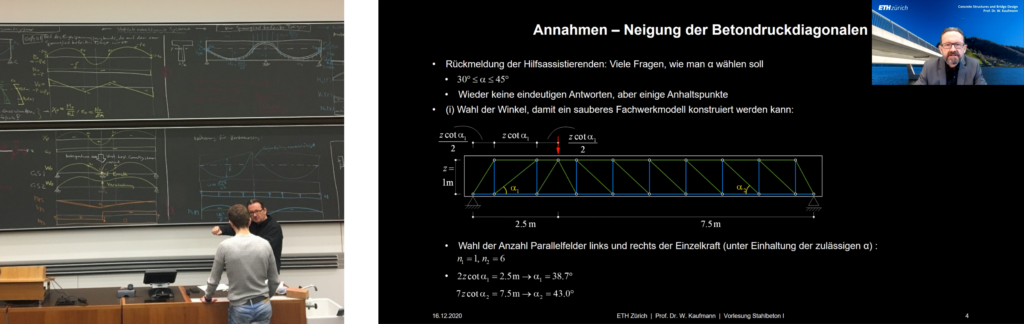
Wie Sie angesichts meines Werdegangs in der Praxis schon vermutet haben könnten, konzentriert sich unsere Forschung auf Fragestellungen, die wir als wichtig und praxisrelevant erachten. Sie umfasst innovative Themen, aber auch das, was ein namhafter Kollege einmal als “Brot-und-Butter-Forschung” bezeichnete: Untersuchungen zum Verhalten von konventionellen Betontragwerken.
Dies ist notwendig, da das mechanische Verhalten von Betontragwerken bei weitem noch nicht vollständig geklärt ist – was angesichts der Unmenge an existierenden Betonbauwerken erstaunen mag. Selbstverständlich sind wir heute in der Lage, sichere und effiziente Betontragwerke zu konstruieren, insbesondere auf der Grundlage des unteren Grenzwertsatzes der Plastizitätstheorie (mehr dazu in meinem nächsten Blogbeitrag).
Bei der Beurteilung der Tragsicherheit bestehender Bauwerke, die vor Jahrzehnten anhand von semi-empirischen Bemessungsregeln dimensioniert und bewehrt wurden, sind unsere modernen Bemessungsmethoden jedoch selten zielführend, da solche Bauwerke deren Voraussetzungen nicht erfüllen.
Darüber hinaus sind bestehende Bauwerke oft kombiniert beansprucht, was die Beurteilung ihrer tatsächlichen Tragfähigkeit sehr anspruchsvoll macht. In der Folge weisen viele bestehende Betontragwerke rechnerische Tragsicherheitsdefizite auf.
Eine Vielzahl von Bauwerken zu verstärken oder gar zu ersetzen, ohne sicher zu sein, dass dies tatsächlich notwendig ist, ist aber gewiss nicht nachhaltig. Daher ist ein verbessertes Verständnis des mechanischen Verhaltens von Betontragwerken unerlässlich, um den ökologischen Fussabdruck der Bauindustrie zu reduzieren. Ehrlich gesagt finde ich dies sogar dringender als die Entwicklung innovativer, nachhaltiger Lösungen.
Nichtsdestotrotz beschäftigen wir uns auch mit Letzterem. In beiden Fällen kombinieren wir mechanische Modelle mit grossmassstäblichen Versuchen und numerischen Analysen. Nähere Angaben zu unseren Forschungsgebieten und -methoden finden Sie auf unserer Website https://kaufmann.ibk.ethz.ch/de/. Sie werden zukünftig ein Hauptbestandteil dieses Blogs sein.

Last but not least erbringen wir auch Dienstleistungen für Berufspraxis und Gesellschaft. Diese Aktivitäten umfassen einerseits anspruchsvolle Gutachten – mit denen wir die Experten aus der Praxis nicht konkurrenzieren, sondern unterstützen – und andererseits die aktive Mitarbeit in Berufsverbänden, Expertengremien und Normkommissionen. Damit wollen wir zur Lösung der Herausforderungen unserer Gesellschaft beitragen. Auch diese Aktivitäten werden Gegenstand zukünftiger Beiträge sein.
Vielmehr wollen wir eine Plattform für den Austausch und die Diskussion im konstruktiven Ingenieurbau schaffen.
Wie gesagt besteht das Ziel dieses Blogs nicht nur darin, über unsere Aktivitäten zu informieren. Vielmehr wollen wir eine Plattform für den Austausch und die Diskussion im konstruktiven Ingenieurbau schaffen. Aus diesem Grund fordern wir Sie auf, uns Ihr Feedback zukommen zu lassen, egal ob positiv oder negativ. Wir beabsichtigen auch Gastbeiträge in diesen Blog aufzunehmen, und laden Sie ein, uns zu kontaktieren wenn Sie daran interessiert sind einen Beitrag zu verfassen.
Wir hoffen, dass Ihnen die Idee dieses Blogs gefällt und Sie uns zukünftig regelmässig besuchen werden. Bitte teilen Sie uns Ihre Meinungen und Wünsche als Kommentar mit.
Walter Kaufmann