Link zur deutschen Version: Eine neue Kombination aus Maschinellem Lernen und der Finiten-Elemente-Analyse.
Many of the previous blog posts have already emphasised the importance of sustainability in the design of concrete structures (Blog Rebecca Ammann, Blog Sophia Kuhn). This blog post presents a different method towards finding design methods that allow for a more efficient design or verification of reinforced concrete structures to reduce the concrete consumption and thus build more sustainably.
Current design tools for reinforced concrete (RC) structures mostly rely on linear elastic finite element analyses (LFEA). They approximate the strongly nonlinear material behaviour of RC with linear models and tend to be overly conservative (Thoma et al. 2014). Such an approximation can hence lead to economically as well as environmentally inefficient designs of RC structures.
On the other hand, several different models for non-linear finite element analyses (NLFEA) exist, which comprise different methodological approaches. One example is the implementation of the mechanically consistent Cracked Membrane Model (CMM, Kaufmann and Marti 1998, Thoma et al. 2014). This method can reproduce the real behaviour of RC structures more accurately compared to LFEA and can be applied universally, also for discontinuous structures (see also previous blog by Marius Weber). However, NLFEA simulations are rarely carried out in practise due to their computational inefficiency and their complex dependency on multiple uncertain (material) parameters. More than one non-linear calculation is rarely executed, making it difficult to investigate different design or verification scenarios or even to optimise a RC structure.
In contrast, novel digital processes, such as machine and deep learning (ML/DL) systems as well as differentiable simulation are the current state-of-the-art for differentiable modelling and gradient-based optimisation. It has been shown that ML and DL can discover patterns and generalise well from data (LeCun et al. 2015, Shen et al. 2023). Once they are trained, they are fast in predicting desired performances. Recent advances in physics-based machine learning (PBML) have shown the potential of ML methods in combination with conventional computational physics models over various domains, such as in fluid dynamics, solid mechanics as well as structural mechanics. Physics-informed neural networks (PINNs, Raissi et al. 2019) are one example of this type of machine learning, where compared to standard neural networks (NN), the underlying physical equation such as a differential equation is incorporated directly in the loss term of the neural network. Figure 1 shows an example of such a PINN for an RC beam, according to the Euler-Bernoulli beam equation. The PINN only requires the locations x at which the differential equation should be evaluated as input data. Once trained, it can predict the vertical deformations (w) and bending moments (M) of a simply supported beam given the location x along the beam for a given set of geometry, material parameters and loading.
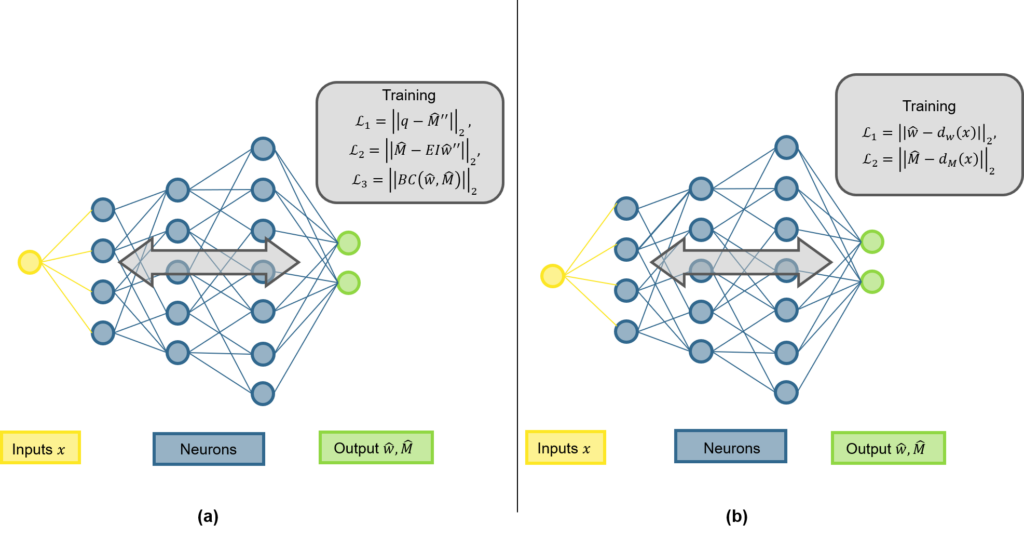
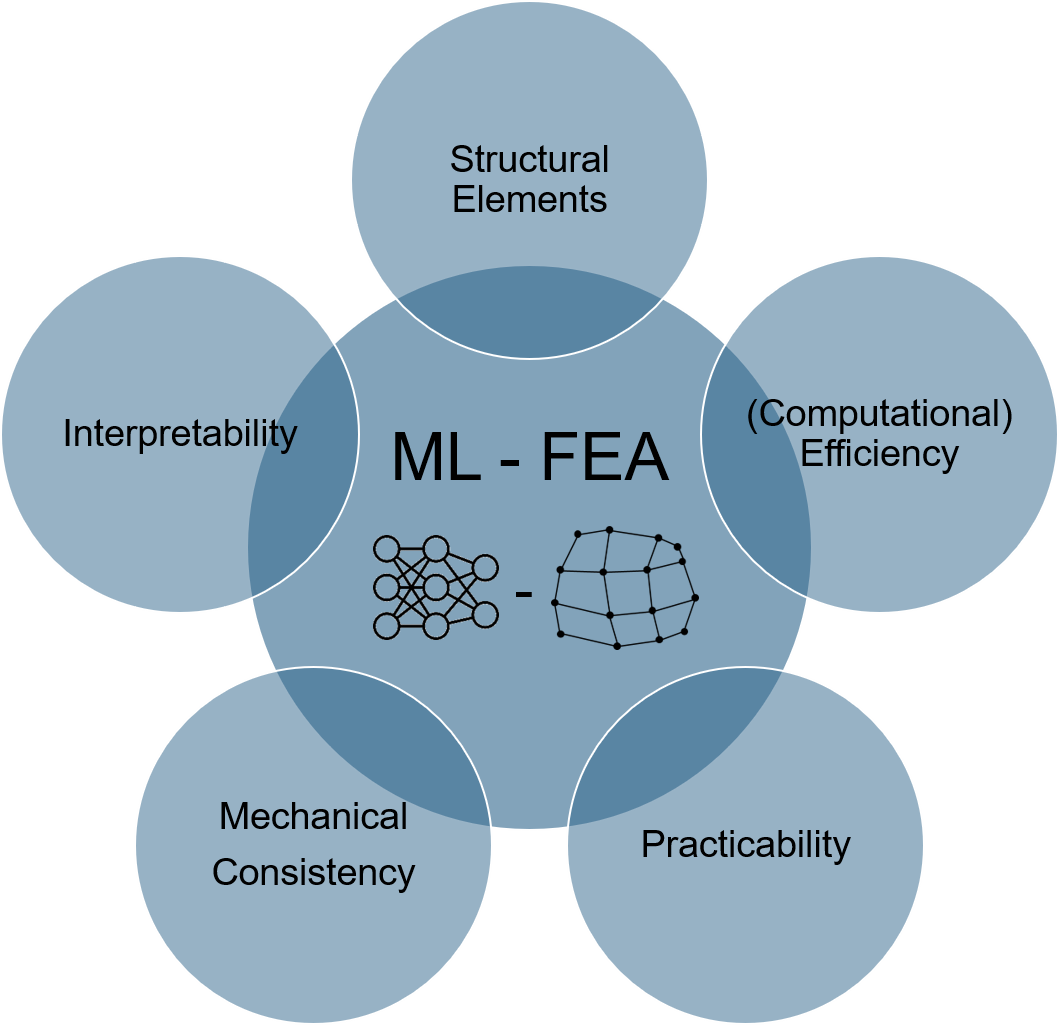
For the application of novel ML / DL methods in the construction sector, a crucial point is to include domain knowledge (e.g. the differential equation of the Euler-Bernoulli beam) in the ML systems, as can be done with PINNs, and ensure validity as well as acceptance with reliability assessments familiar to engineers. In addition, the construction sector is not a domain where typically a lot of data is available to train ML models on, which is why incorporating physics-based methods would be beneficial. Even though the emerging novel PBML methodologies show promising results, most of these methods fail to generalise outside of the parameter space they are trained on, restricting the application possibilities to problems far from real-world applications. Hence, we intend to develop a novel mechanics-based machine learning methodology for efficient modelling of RC elements. This novel methodology shall be developed by combining ML with traditional FEA approaches, with the main objectives shown in Figure 2: The method should be developed on a structural element level, i.e. for individual beams, plates or shells and has the goal of increasing the efficiency of the current methodology. This shall be reached by developing interpretable, mechanics-based methods in the current framework of FEA and optimally implementing it in a standard FEA software for practicability.
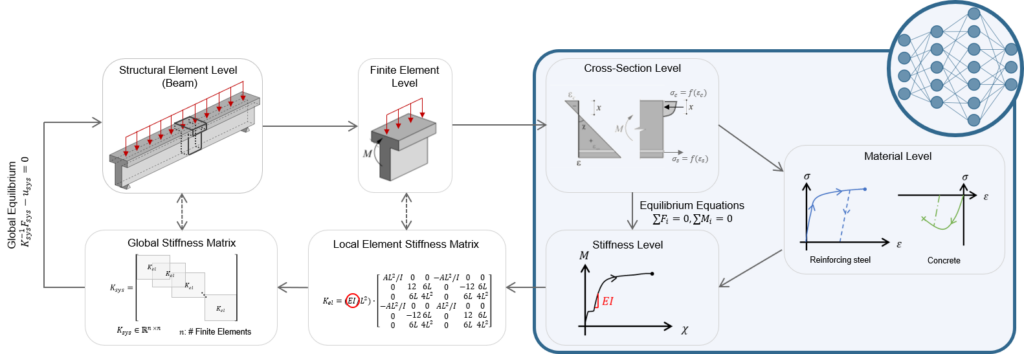
To exemplify the methodology, a preliminary study was carried out, investigating a simplified NLFEA of a beam element. Figure 3 shows the workflow of this simplified NLFEA, where the simply supported beam is first divided into finite beam elements, which are analysed at the cross-section level to determine the local and then global stiffness matrix to finally evaluate the global equilibrium. The goal was then to replace the highly iterative and time-consuming calculation at the cross-section level in the analysis with a standard NN (see Figure 3). This NN is trained with data from parametrised simulations of moment-curvature graphs. The parametrisation includes variations of material strengths and stiffnesses, height and width of the finite element, etc. In the end, the NN receives the moment at the finite element as an input and predicts curvatures and corresponding tangent stiffnesses of the cross-section (EI). By replacing this calculation step with a NN, a surrogate finite element is created which doesn’t require iterations on the cross-section level. This finite element can be used for any type of structure, which can be modelled with RC beam elements, hence allowing for larger generalisability. The next steps are now to translate these findings to shell structures and incorporate physics in the NN as explained above. Ultimately the developed ML-FEA method will be compared with state-of-the-art NLFEA software.
In conclusion, with this combination of ML methodologies and FEA we hope to create a tool which will allow for more detailed design or verification of existing structures and in this manner help utilising RC more efficiently. If you are interested in this topic, stay tuned and we will be glad to tell you about the developments of this project as soon as possible.
Vera Balmer