Link to the English version: A novel combination of Machine Learning and the Finite Element Analysis.
Einige der letzten blog Beiträge haben sich schon der Nachhaltigkeit im Betonbau gewidmet (z.B. Blog Rebecca Ammann, Blog Sophia Kuhn). In diesem Blogpost wird eine neue Methodik vorgestellt, die effizientere Entwürfe und Überprüfungen von bestehenden Stahlbetonbauten ermöglichen soll, sodass die Verwendung von Beton reduziert werden kann und wir nachhaltiger bauen können.
Bestehende Entwurfsmethoden für Stahlbetonbauten basieren hauptsächlich auf den linear-elastischen Finite-Elemente-Analysen (LFEA). Sie approximieren das stark nichtlineare Materialverhalten von Stahlbeton mit linearen Modellen und sind deshalb teils sehr konservativ (Thoma et al. 2014). Solche Annäherungen können deshalb zu wirtschaftlich wie auch umwelttechnisch ineffizienten Designs von Stahlbetonbauten führen. Andererseits bestehen viele Modelle für nichtlineare Finite-Elemente-Analysen (NLFEA), welche unterschiedlichen methodologischen Ansätzen folgen. Ein Beispiel ist die Implementierung des mechanisch konsistenten Gerissenen Scheibenmodell (engl.: Cracked Membrane Model, Kaufmann und Marti 1998, Thoma et al. 2014). Diese Methode kann das Materialverhalten von Stahlbeton im Vergleich zur LFEA genauer abbilden und ist universell einsetzbar, auch bei diskontinuierlichen Strukturen (siehe auch füherer Blogbeitrag von Marius Weber). Dennoch werden NLFEA selten in der Praxis verwendet, da sie rechnerisch ineffizient sind und komplexe Abhängigkeiten von verschiedenen Materialparametern aufweisen. Nur selten wird mehr als eine NLFEA Berechnung ausgeführt, was es schwierig macht, unterschiedliche Lastsituationen oder Überprüfungsszenarien zu betrachten oder sogar Strukturen zu optimieren.
Neue digitale Prozesse, wie maschinelles oder tiefes Lernen (engl.: Machine and Deep Learning, ML / DL), wie auch differenzierbare Simulation sind hingegen der neuste Stand der Technik bezüglich ableitungsbasierten Optimierungsmethoden. Für ML und DL wurde zum Beispiel gezeigt, dass diese Methoden neue Muster aus Daten erkennen können und gut über Datensätze hinweg generalisieren können (LeCun et al. 2015, Shen et al. 2023). Sobald sie trainiert sind, können sie schnell gewünschte Zielparameter vorhersagen. Neue Entwicklungen in physik-basiertem maschinellem Lernen (PBML) haben gezeigt, dass die Kombination von ML mit bestehenden computergestützen physikalischen Modellen ein grosses Potenzial birgt. Dies wurde in diversen Anwendungsgebieten wie zum Beispiel Fluiddynamik, Festkörpermechanik wie auch Strukturmechanik gezeigt. Ein Beispiel von PBML sind physik-informierte neuronale Netze (PINNs, Raissi et al. 2019), bei denen im Vergleich zu konventionellen neuronalen Netzen (NN) die zugrundeliegenden physikalischen Gleichungen, z.B. Differenzialgleichungen, direkt in die Verlustterme des NNs eingefügt werden. Abbildung 1 zeigt ein Beispiel eines PINNs für einen Stahlbetonbalken mit Euler-Bernoulli Balkengleichung. Als Datensatz werden nur die Stellen x benötigt, an denen man die Differenzialgleichung auswerten möchte. Sobald das PINN trainiert ist, kann es für gegebene Geometrie, Materialparameter und Last die Verschiebungen (w) und Momente (M) eines einfach gelagerten Balkens an der gewünschten Stelle x vorhersagen.
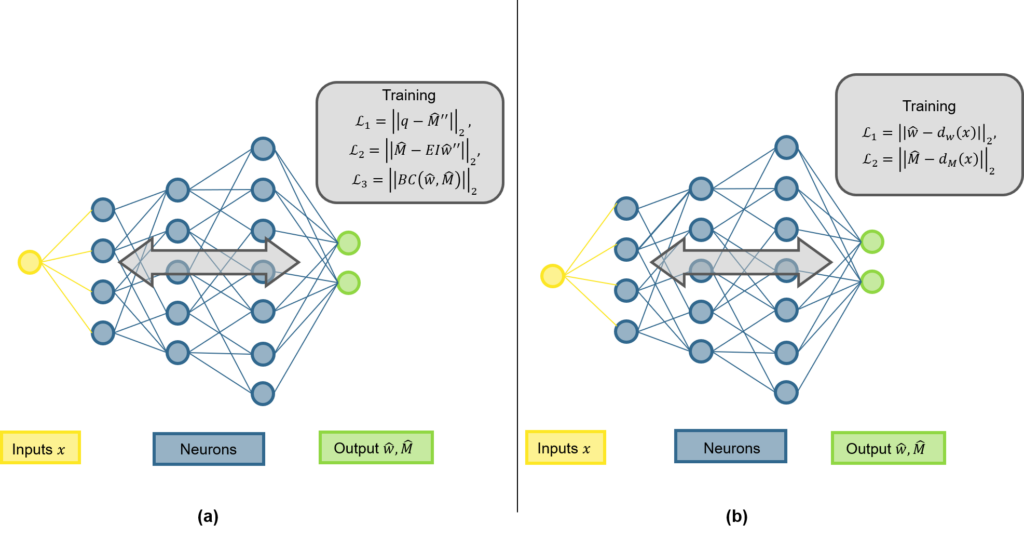
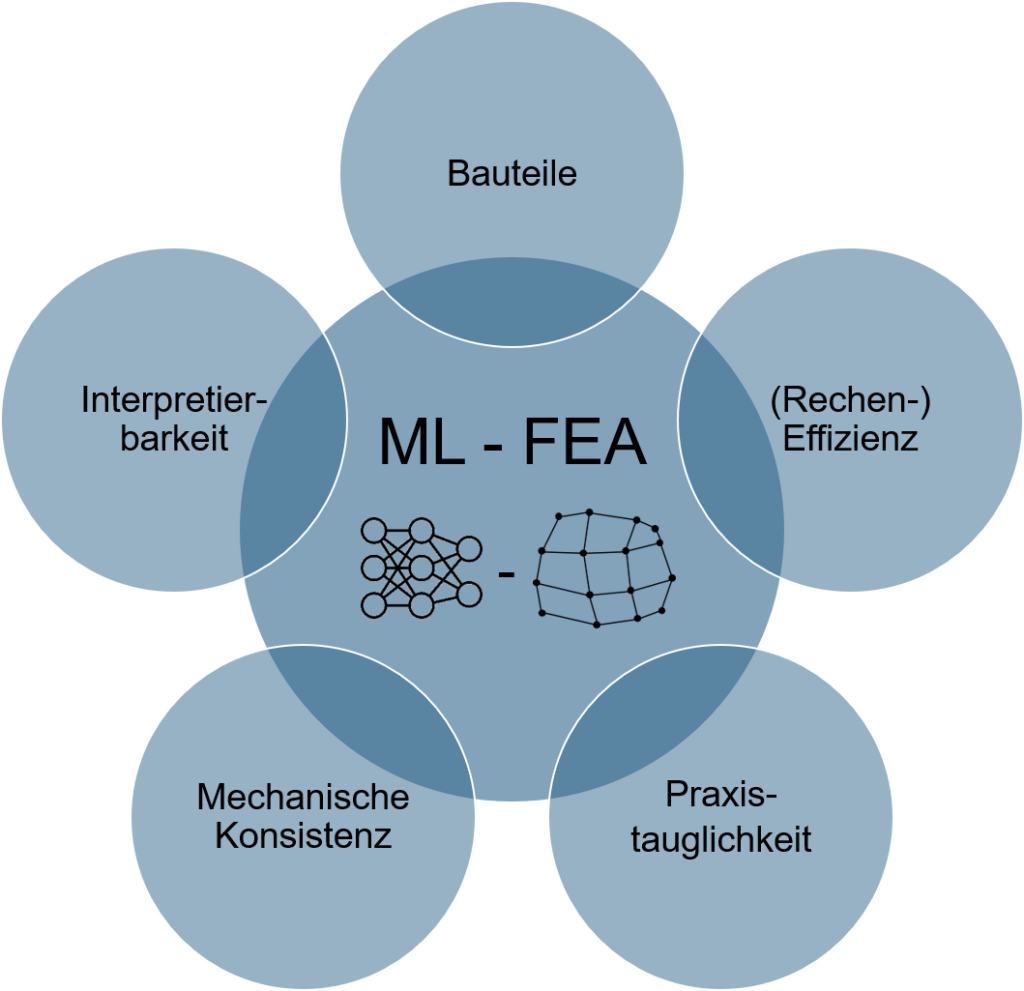
Damit man ML / DL – Methoden im Bausektor anwenden kann, ist es wichtig, grundlegende Theorien des Anwendungsgebiets (z.B. die Differenzialgleichung des Euler-Bernoulli-Balkens) miteinzubeziehen bei der Erstellung der Methode, wie es zum Beispiel bei PINNs möglich ist, sodass eine Akzeptanz wie auch Validierungsmöglichkeit geschaffen wird. Zusätzlich gibt es im Bausektor typischerweise wenig verfügbare Daten mit denen man ein ML Modell trainieren könnte, weshalb es noch wichtiger ist, physik-basierte Methoden zu verwenden. Obwohl diese Methoden gute Resultate zeigen, sind sie limitiert in ihrer Generalisierbarkeit ausserhalb des Parameterraums in dem sie trainiert wurden, was die Anwendung solcher Methoden auf reale Probleme im Betonbau äusserst einschränkt. Deshalb wollen wir eine neue Methode entwickeln, die ML mit traditionellen FEA kombiniert, wobei die Hauptanliegen in Abbildung 2 dargestellt sind: Die Methodik soll auf Bauteilebene entwickelt werden, das heisst für einzelne Balken, Platten oder Schalenelemente und schlussendlich die Effizienz der zur Zeit verwendeten FE-Methoden verbessern. Dies soll durch eine interpretierbare Mechanik-gestützte Methode, die in die FEA eingegliedert wird erreicht werden, idealerweise mit einer praxistauglichen Implementierung in einer kommerziellen FE-Software.
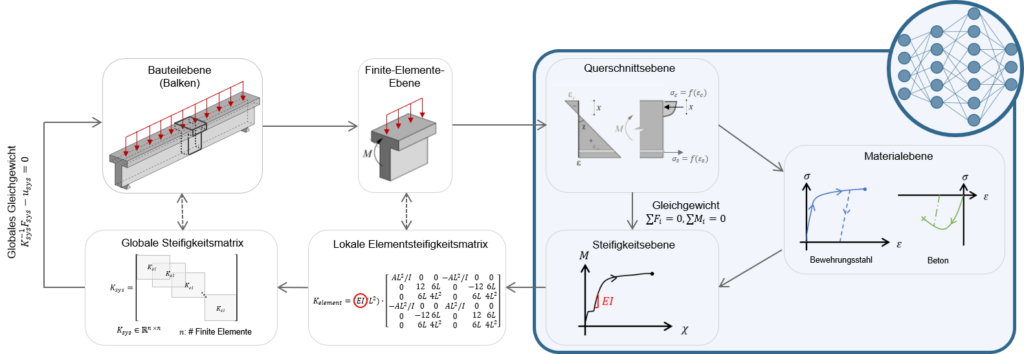
Zur Veranschaulichung der Idee wurde eine Vorstudie durchgeführt, die eine vereinfachte NLFEA eines Balkenelements untersucht. Abbildung 3 zeigt den Ablauf dieser vereinfachten NLFEA, bei der zuerst der einfach gelagerte Balken in finite Elemente unterteilt wird, welche auf der Querschnittsebene analysiert werden, die dann zu den Werten für die lokalen und globalen Steifigkeitsmatrizen führen, um schlussendlich das globale Gleichgewicht zu lösen. Das Ziel war nun, die iterative und zeitaufwändige Berechnung auf Querschnittsebene durch ein normales NN zu ersetzen (siehe Abbildung 3). Das NN wird auf Daten von parametrisierten Simulationen trainiert. Die Parametrisierung enthält Variationen von Materialsteifigkeiten und -stärken wie auch von Breite und Höhe des finiten Elements, etc. Zum Schluss werden dem NN als Input das Moment am finiten Element gegeben und es kann dann Krümmungen und zugehörige Tangentensteifigkeiten (EI) des Querschnitts vorhersagen. Durch den Ersatz dieses Berechnungsschrittes wird ein stellvertretendes finites Element erstellt, welches für alle mit Balkenelementen modellierbare Strukturen eingesetzt werden kann und dadurch zu grösserer Generalisierbarkeit führt. Als nächste Schritte sollen diese Resultate nun für Schalenelemente adaptiert werden und physikalische Zusammenhänge im NN eingebracht werden gemäss den Erläuterungen oben. Zuletzt wird die entwickelte ML-FEA Methode mit dem aktuellsten Stand der Technik von NLFEA Methoden verglichen.
Zusammenfassend hoffen wir mit dieser Kombination von ML und FEA Methoden ein neues Werkzeug zu entwickeln, mit dessen Hilfe Entwurf und Überprüfung von bestehenden Bauten detaillierter durchgeführt werden können und somit Stahlbeton effizienter eingesetzt werden kann. Falls Sie Interesse an diesem Thema haben, bleiben Sie dran, wir werden Sie gerne über die aktuellsten Entwicklungen dieses Projekts auf dem Laufenden halten.
Vera Balmer