Link to the English version: Ductility and rotation capacity of structural concrete
Was ist Duktilität? Warum brauchen wir sie?
Die Duktilität ist ein allgegenwärtiges Konzept im Bauingenieurwesen und im Stahlbetonbau, dem Feld um das sich dieser Blogpost handelt.
Im Erdbebeningieurwesen haben bekannte Autoren folgende Definition der Duktilität vorgeschlagen.
Der Begriff Duktilität bezeichnet die Fähigkeit eines Tragelementes oder Tragwerks, sich nicht nur elastisch, sondern unter Aufrechterhaltung des Tragwiderstandes auch plastisch zu verformen.
(Paulay, Bachmann, Moser ,1990: Erdbebenbemessung von Stahlbetonhochbauten)
The term “ductility” in structural design is used to mean the ability of a structure to undergo large deformations in the postelastic range without a substantial reduction in strength.
(Park, 1991: Ductility of Structural Concrete)
Die Definitionen stammen aus dem Erdbebeningenieurwesen und zielen darauf ab übermässige Schäden bei grossen plastischen Verformungen zu vermeiden. Daher werden manchmal geringe Lastabfälle, oder Entfestigung akzeptiert. Dies ist im Bauingenieurwesen unüblich und unkonservativ, da die meisten Einwirkungen lastgesteuert sind und Versagen bei Höchstlast eintritt.
Paulay, Bachmann und Moser (1990) schlagen vor, je nach Massstab verschiedene Arten der Duktilität zu betrachten, nämlich Dehnungsduktilität auf Materialebene, Krümmungsduktilität auf Querschnittsebene, Rotationsduktilität für plastische Gelenke und die Verschiebeduktilität bei statischen Systemen. Die Duktilität wird jeweils als Verhältnis der betrachteten Grösse (z.B. Dehnung, Krümmung) bei Versagen und bei Fliessbeginn berechnet.
Im Bauingenieurwesen ist die Duktilität in der SIA 260 (2013) wie folgt definiert:
Durch irreversible Verformungen und Energiedissipation charakterisiertes, in der Regel auf die Grenze des elastischen Verhaltens bezogenes plastisches Verformungsvermögen.
Im Bauingenieurwesen ist Duktilität notwendig um die Plastizitätstheorie anzuwenden, um Lastumlagerungen zu ermöglichen und um Eigenspannungszustände vernachlässigen zu können. Dieses Konzept findet sich auch in Normen, wie den SIA Normen oder den Eurocodes wieder. Laut SIA 262 (2013) darf die Plastizitätstheorie nur angewendet werden, wenn duktiles Verhalten sichergestellt werden kann. Lastumlagerungen sind bei kleinem Verhältnis x/d, duktilem Bewehrungsstahl und normalfestem Beton erlaubt. Die Eurocodes erlauben das Vernachlässigen von Eigenspannungszustände, wie Temperatureffekten, differentiellen Setzungen und Schwinden, falls das Verformungsvermögen und das Rotationsvermögen genügend sind (n.b. in der englischen Version des Eurocode 2 ist Verformungsvermögen zu «ductility» übersetzt). Es gibt keine Angabe zur Bestimmung des Verformungsvermögens, aber ein Nachweis des Rotationsvermögens ist in der Norm enthalten (siehe zweiter Abschnitt).
Während die exakte Definition der Duktilität nicht eindeutig ist, sind die meisten Autor:innen sich einig warum duktil gebaut werden sollte. Die Argumente können grob zu zwei Hauptideen zusammengefasst werden:
- Verhindern von unvorhergesehenem Versagen (Versagensankündigung, Robustheit erreichen, Sicherheit bei Erdbeben oder anderen aussergewöhnlichen Einwirkungen)
- Umlagerung von Schnittkräften (Biegemomentenverteilungen die nicht der elastischen entsprechen, Vernachlässigung von Eigenspannungszuständen)
Ein bekanntes Beispiel, wo Duktilität das Versagen verhindert hat, ist die Reussbrücke Wassen, die grosse Setzungen nach dem Unwetter von 1987 überlebt hat und repariert werden konnte (Abbildung 1).

Ist Stahlbeton duktil? Wie stellt man das bei der Bemessung sicher?
Wie gerade gesehen kann Stahlbeton duktil sein. Es stellt sich die Frage, wie bei der Bemessung bestimmt werden kann ob ein Bauwerk ausreichend duktil sein wird. Hier werden zwei Vorgehensweisen vorgestellt.
In der Schweizer Baupraxis wird Duktilität durch bestehendes Wissen über günstige Konstruktionsmassnahmen erreicht. Beispiele für solche Massnahmen sind die Wahl von angemessenen, bewährten Materialien, Mindestbewehrungen und Verbügelung um spröde Schub- oder Druckzonenversagen zu vermeiden. Die Massnahmen stützen auf Erfahrung und experimentell validierten Forschungsergebnissen ab, was gleichzeitig ihr grösster Nachteil ist. Während sie in Standardfällen sehr effizient sind, erschweren sie zum Beispiel die Verwendung von neuen Materialien.
Die SIA 262 erlaubt die Umlagerung von Schnittkräften ohne Nachweis des Verformungsvermögens, falls die Druckzonenhöhe begrenzt wird, die Duktilitätsklasse des Betonstahls mindestens B500B ist und die Druckfestigkeitsklasse tiefer als C50/60 ist. Der Eurocode 2 enthält ähnliche Angaben, aber erlaubt hochfesten Beton unter Voraussetzung einer strikteren Begrenzung der Betondruckzonenhöhe. Daraus kann man implizit ableiten, dass Bauteile, die diese Bedingungen erfüllen, als duktil angesehen werden können.
Werden diese Bedingungen nicht erfüllt, gilt es zu überprüfen ob das Rotationsvermögen von erwarteten plastischen Gelenken grösser ist als der Rotationbedarf. Während es kein direkter Nachweis der Duktilität ist, stellt es sicher, dass die plastischen Rotationen, die zur Biegemomentenumlagerung bei Bemessungslast nötig sind, ohne Versagen aufgenommen werden können. In diesem Beitrag zeige und vergleiche ich zwei Methoden um das Rotationsvermögen zu berechnen.
Der Eurocode 2 (2004) schlägt bilineare Zusammenhänge zwischen dem plastischen Rotationsvermögen und xu/d vor, wobei xu die Höhe der Druckzone ist und d die statische Höhe. Die Norm enthält verschiedene Zusammenhänge für normalfesten und hochfesten Beton, und Betonstahl der Klassen B500B und B500C. Die Zusammenhänge dürfen mit einem Faktor multipliziert werden, der der Schubschlankheit Rechnung trägt. Der Hauptnachteil dieser Methode ist, dass es sich um eine «Black Box» handelt, sodass es schwierig für Ingenieure ist die Plausibilität der Resultate zu prüfen.
Sigrist und Marti (1994) schlagen eine allgemein gültige Methode und eine vereinfachte Bemessungsmethode für das Rotationsvermögen vor, die beide auf dem Zuggurtmodell basieren. Bei der vereinfachten Methode wird die mittlere plastische Krümmung bei Versagen mit einer angenommenen Länge des plastischen Gelenks Lpl = d multipliziert (d = statische Höhe). Die Autoren geben zwei analytische Ausdrücke für die mittlere plastische Krümmung an, je nachdem ob Reissen der Bewehrung oder ein Betondruckversagen massgebend wird. Bei tiefen bis moderaten mechanischen Bewehrungsgehalten wird Reissen der Bewehrung massgebend, bei vergleichsweise hohen mechanischen Bewehrungsgehalten das Betondruckversagen.
Die allgemein gültige Methode wird hier nicht im Detail vorgestellt. Sie folgt der gleichen Idee, die Stahlspannungen in der plastischen Zone zu bestimmen. Zusätzlich berücksichtigt sie den Verlauf der Kraft im Zuggurt, der benutzt werden kann, um die Länge des plastischen Gelenks zu bestimmen, und die Biegemomentenumlagerung beim Fliessen des plastischen Gelenks.
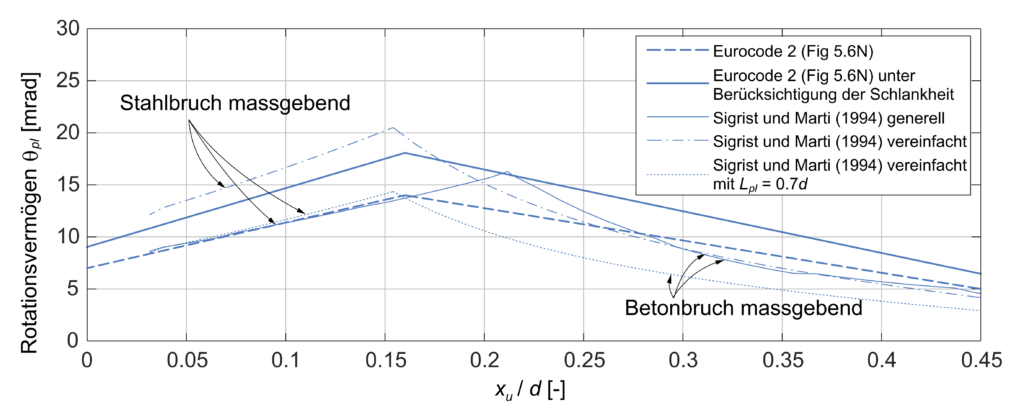
Abbildung 2 zeigt einen Vergleich der drei erwähnten Methoden am Beispiel eines Zweifeldträgers unter Gleichlast mit statischer Höhe d = 1200 mm. Das Basisbeispiel wurde mit Beton C30/37, Betonstahl B500B, Schlankheit L/d = 20 (L = Spannweite) und einem Rissabstand sr = 150 mm berechnet. In Abbildung 3 werden diese Parameter einzeln variiert. Die Kurven starten bei der Mindestbewehrung um ein Sprödversagen bei Rissbildung zu vermeiden.
Die bilinearen Kurven des Eurocode spiegeln die Form der Kurven auf Basis des Zuggurtmodells wieder, bei welchen der Knick den Übergang zwischen Stahl- und Betonversagen ausdrückt. Der Unterschied zwischen den beiden Methoden von Sigrist und Marti (1994) bei kleinen mechanischen Bewehrungsgehalten ist hauptsächlich der Abschätzung der plastischen Gelenklänge in der vereinfachten Methode geschuldet: Wenn eine Gelenklänge von Lpl = 0.7 d anstelle Lpl = d angenommen wird sind die Kurven fast identisch. Die unbekannte Länge des plastischen Gelenks ist einer der Hauptnachteile der vereinfachten Methode.
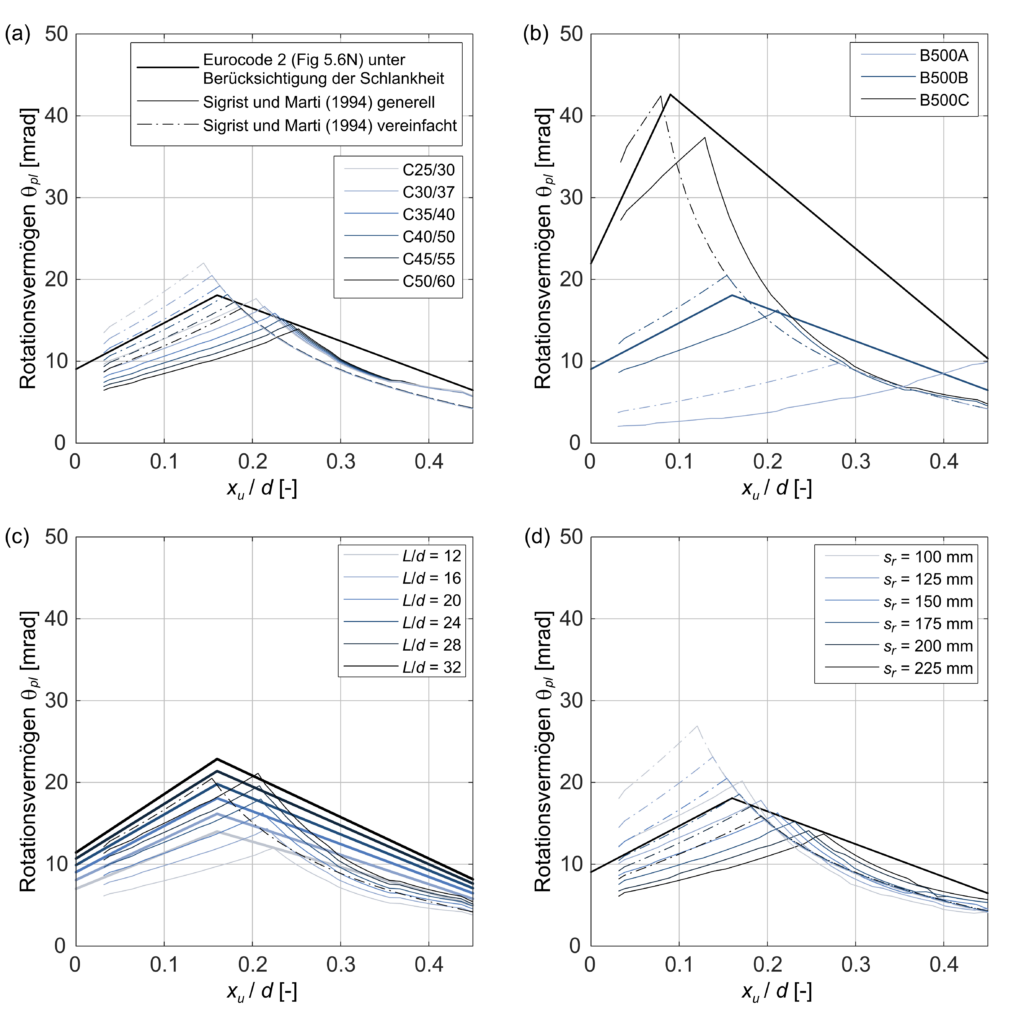
Abbildungen 3 (a) bis (d), zeigen den Einfluss der Betondruckfestigkeitsklasse, der Duktilitätsklasse der Bewehrung, der Schlankheit und des Rissabstandes.
Der Eurocode gibt eine einzelne Kurve für das Rotationsvermögen aller Betondruckfestigkeitsklassen < C50/60 an. Die Modelle basierend auf dem Zuggurtmodell ergeben eine Abnahme des Rotationsvermögens mit höherer Druckfestigkeit, falls Stahlversagen massgebend ist, und kaum einen Einfluss falls Betonversagen massgebend ist. Das mag auf ersten Blick kontraintuitiv scheinen, liegt aber daran, dass die Betonzugfestigkeit laut Zuggurtmodell in direktem Bezug zur Verbundspannung steht. Eine höhere Verbundspannung bedeutet einen grösseren Einfluss der Zugverfestigung und daher eine kleinere mittlere Stahlspannung im Risselement und ein geringeres Rotationsvermögen.
Wird duktilerer Stahl verwendet, so ergeben die Modelle wie erwartet ein grösseres Rotationsvermögen und Betonversagen wird bei tieferen mechanischen Bewehrungsgehalten massgebend.
Laut Eurocode dürfen die bilinearen Zusammenhänge mit einem Faktor kλ multipliziert werden, um die Schlankheit des Bauteils zu berücksichtigen. Die allgemein gültige Methode von Sigrist und Marti (1994) zeigt eine ähnliche Zunahme des Rotationsvermögens mit der Schlankheit, doch die vereinfachte Methode berücksichtigt die Schlankheit nicht.
Die Methoden auf Basis des Zuggurtmodells ergeben, dass ein grösserer Rissabstand einen negativen Einfluss auf das Rotationsvermögen hat. Der bilineare Zusammenhang laut Eurocode berücksichtigt den Rissabstand nicht. Das kann auch als Vorteil gewertet werden, da die Abschätzung der Rissabstände schwierig ist.
Hier sind die wichtigsten Schlussfolgerungen aus der Parameterstudie zusammengefasst
- Die Länge des plastischen Gelenks hat einen grossen Einfluss auf die Resultate der vereinfachten Methode nach Sigrist und Marti (1994) doch es ist schwierig sie vorgängig zu bestimmen.
- Der Einfluss der Schlankheit wird in der vereinfachten Methode nicht berücksichtigt.
- Der Eurocode gibt tendenziell höhere Schätzungen des Rotationsvermögens, wenn Betonversagen massgebend ist, da der vorgeschlagene Zusammenhang linear ist (im Gegensatz zu den nichtlinearen Kurven der anderen Methoden)
Eine spezifische Bemessungsaufgabe ergibt einen Punkt in den oberen Diagrammen. Da sowohl die Methode nach Eurocode und die vereinfachte Methode nach Sigrist und Marti (1994) sehr einfach anzuwenden sind, macht es Sinn in Praxis beide zu vergleichen.
Die Unterschiede zwischen den Methoden mögen gross scheinen, aber es ist wichtig anzumerken, dass die experimentellen Resultate ebenfalls streuen. Das rechtfertigt es einfachere Methoden beim Nachweis des Rotationsvermögens zu verwenden (anstelle komplizierter Modelle) aber stellt solche Berechnungen grundsätzlich in Frage.
Ein direkter Nachweis der Duktilität (als Verhältnis von z.B. der Rotation bei Versagen und Fliessbeginn) wird bei statischen Problemen nicht praktiziert. Obwohl eine solche Berechnung der Rotationsduktilität in plastischen Gelenken in der Literatur diskutiert wird, gibt es kaum Informationen zu Duktilitätsanforderdungen.
Was ist der Zusammenhang zwischen dem Nachweis des Verformungsvermögens und der Duktilität?
Während Bauingenieur:innen im allgemeinen mit dem Konzept der Duktilität vertraut sind, wird sie oft mit anderen, verwandten Konzepten, wie zum Beispiel dem Verformungsvermögen und dem Verformungsbedarf verwechselt.
Die SIA 260 definiert die Duktilität als Verformungsvermögen, das durch irreversible Verformungen und Engergiedissipation charakterisiert ist, wobei das Verformungsvermögen elastische und plastische Verformungen eines Bauwerks bis zum Versagen umfasst. Ein duktiles Bauteil ist dementsprechend eins, das vor dem Versagen grosse inelastische Verformungen erträgt während es Energie dissipiert, und also nicht entfestigt. Das Konzept der Duktilität ist nicht direkt von den Einwirkungen oder dem Verformungsbedarf abhängig.
Im Gegensatz dazu wird beim Nachweis des Verformungsvermögens laut Eurocode 2 überprüft ob der Verformungsbedarf im Bemessungsfall geringer ist als das Verformungsmögen. Falls die Schnittgrössen insgesamt oder in einer Region gering sind, kann der Nachweis erfüllt sein, obwohl das Verformungsvermögen eines Bauteils gering ist. Das hat positive und negative Konsequenzen. Einerseits scheint es unnötig ein hohes Verformungsvermögen in Bereichen zu bieten, die wohl nie ins Fliessen kommen. Andererseits können unvorhergesehene Lasten oder Eigenspannungszustände zu unerwartet hohem Verformungsbedarf führen, sodass mangelndes Verformungsvermögen fatal sein könnte.
Eine der Hauptschwierigkeiten beim Nachweis des Verformungsvermögens besteht in der Berechnung des Verformungsbedarfs, da er von Eigenspannungszuständen abhängig ist. Das kann anschaulich am Beispiel eines Experiments an einem zweifeldrigen Plattenstreifen gezeigt werden (Abbildung 4). Vor Versuchsbeginn wurde dem anfänglich ebenen Versuchskörper ein Eigenspannungszustand aufgezwungen, indem die Auflager verschoben wurden. Dadurch entsteht die gekrümmte Form bei Last 0 kN in Abbildung 4. Es ist intuitiv klar, dass der Rotationsbedarf am Zwischenauflager in diesem Fall höher ist, als im Fall ohne Eigenspannungszustand. Folglich müssen ungünstige Eigenspannungszustände bei der Bestimmung des Verformungsbedarfs berücksichtigt werden.
Im Extremfall müsste man fordern, dass das Verformungsvermögen grösser ist als der Verformungsbedarf bis zum Erreichen der Traglast. In diesem Fall ist das Verformungsvermögen bei jedem beliebigen Eigenspannungszustand ausreichend. Leider gibt die SIA 262 nicht an, wie genau der Nachweis des Verformungsvermögens erfolgen soll und welche Einwirkungen bei der Bestimmung des Verformungsbedarfs zu berücksichtigen sind.

Was können wir schlussfolgern? Wo soll es hingehen?
In diesem Blogpost wurde das Thema der Duktilität bei der Bemessung von Stahlbetonbauteilen unter statischen Lasten eingeführt und zwei einfache Methoden zur Berechnung des Rotationsvermögens wurden aufgezeigt. Dann wurde der Zusammenhang zwischen dem Konzept der Duktilität und dem Nachweis des Verformungsvermögens erklärt.
Ein Problem ist, dass die SIA 262 keine Methoden bereitstellt um die Duktilität von Bauteilen abzuschätzen, die nicht der gängigen Baupraxis entsprechen. Falls z.B. Bewehrungen benutzt werden sollen, die nicht den Duktilitätsklassen B500B oder B500C entsprechen, können Schnittkräfte nur mit Nachweis des Verformungsvermögens umgelagert werden. Das ist eine schwere Einschränkung für innovative Baumaterialien und Fertigungsprozesse, wie z.B. neue Bewehrungsarten oder die Digitale Fabrikation, da die in den Normen gegebenen Methoden nur für spezifische Anwendungen gedacht sind: Die einfachen Berechnungsmethoden für das Verformungsvermögen sind nützlich für Bauteile die in eine Richtung tragen aber sind z.B. nicht auf Platten anwendbar. Ausserdem ist die Bestimmung des Verformungsbedarfs schwierig, da er von Eigenspannungszuständen abhängt.
Aktuelle Forschung zielt darauf ab eine Strategie zur Bemessung von Bauteilen mit niederduktilen, entfestigenden und spröden Elementen zu entwickeln, wobei das Gesamtbauteil duktil bleiben soll.
Dazu werden die Ideen der Kapazitätstheorie mit elastisch-plastischen System verknüpft und Bauteile so bemessen, dass Versagen in duktilen Bereichen eintritt. Ähnliche Ideen sind die Basis von Normbestimmungen um spröde Schubversagen zugunsten von Biegeversagen zu vermeiden.
Gleichzeitig wird in Zusammenarbeit der Professur für Massiv- und Brückenbau an der ETH Zürich und des Instituts für Bauingenieurwesen (IBI) an der Hochschule Luzern eine Versuchsserie an zweifeldrigen Plattenstreifen durchgeführt.
Abbildung 4 zeigt einen Versuch an einem Plattenstreifen, der mit Betonstahl mit hoher Bruchdehnung aber kaum Verfestigung in einem Grossteil des inelastischen Bereichs bewehrt wurde. Dies ist einer in einer Reihe von 21 geplanten Versuchen mit metallischen Bewehrungen verschiedener Duktilität und Festigkeit, sowie nicht-metallischer Bewehrung.
Die Untersuchungen sollen bei der Verwendung von innovativen Materialien und Fertigungsweisen helfen und das Verständnis, sowie das Bewusstsein für Duktilität, Verformungsvermögen und Verformungsbedarf im Stahlbeton stärken.
Nathalie Reckinger
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram