Link zur deutschen Version: Schubtragverhalten von schwach bewehrten Stahlbeton-Scheibenelementen
In developed countries, a huge number of ageing infrastructure objects need to be reassessed to ensure their structural safety. However, current assessment methods for analysing the load-carrying capacity of existing structures are in many cases not sufficient as they are typically based on the same models as the methods used in the design codes for new structures. In particular, the estimation of the shear strength is often deficient due to low transverse reinforcement ratios which were possible due to the ancient code provisions. In my dissertation, which I successfully defended in February, I tried to improve the comprehension of the load-deformation behaviour of reinforced concrete membrane elements with very low amounts of and without vertical reinforcement subjected to in-plane shear and normal forces.
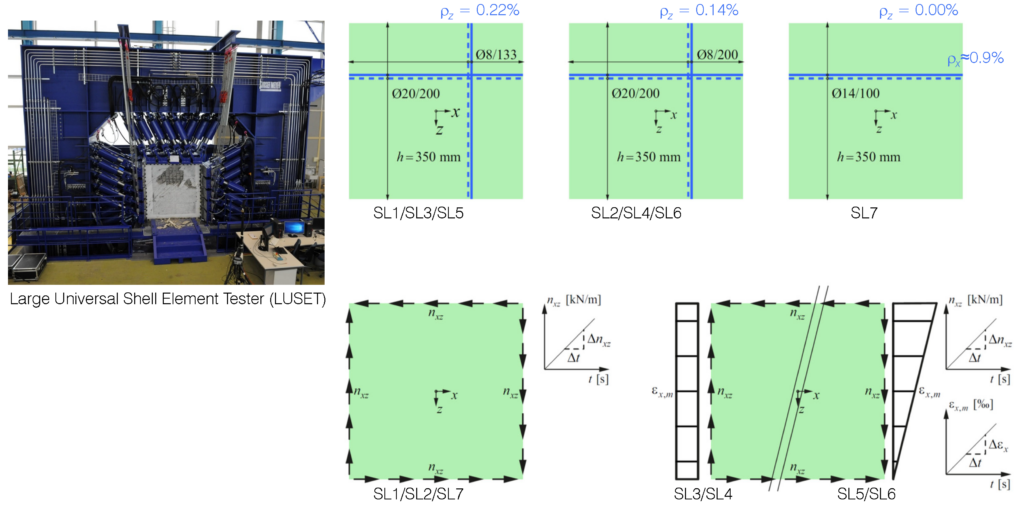
To this end, an experimental test campaign consisting of six large-scale membrane elements with very low amounts of vertical reinforcement of ρz=0.14…0.22%, and one uniaxially reinforced membrane element was carried out. Three panels were tested under pure in-plane shear and four panels were tested under in-plane shear with imposed longitudinal strain with and without gradient over the height of the specimens. The tests were conducted in the newly developed testing facility Large Universal Shell Element Tester (LUSET). The applied modern measurement techniques, namely digital image correlation (DIC) and fibre optic (FO) strain measurements, yielded very valuable and comprehensive data of the full-field deformations and the crack patterns on the concrete surface, and of the continuous strains along the embedded reinforcing bars.
The test results were compared to theoretical models in terms of the global load-deformation behaviour of the tested membrane elements, but also in terms of cracking behaviour and aggregate interlock, i.e. the stress transfer across the cracks in the membrane elements. The model predictions of the cracked membrane model with fixed interlocked cracks (CMM-F), which was originally developed by Professor Walter Kaufmann, were excellent for the panels with very low amounts of vertical reinforcement. The CMM-F, in particular using the rough crack model (RCM) as aggregate interlock model, yielded very good predictions. The RCM is a purely empirical aggregate interlock model, which was fitted based on numerous tests. The CMM-F using Walraven’s more mechanically based two-phase model (TPM), which is the most widely used aggregate interlock model, lead to conservative predictions. This is fortunate in terms of the application of models based on the TPM in design practice (e.g. the shear provisions for members without shear reinforcement in the SIA 262). Another important finding of the experimental campaign regarding the design practice was the confirmation of the well-established recommendation to use a minimum reinforcement ratio of ρz=0.2% for normal strength concrete. It is advised against the tendency to lower this value as e.g. done in the fib MC 2010 or the SIA 262.
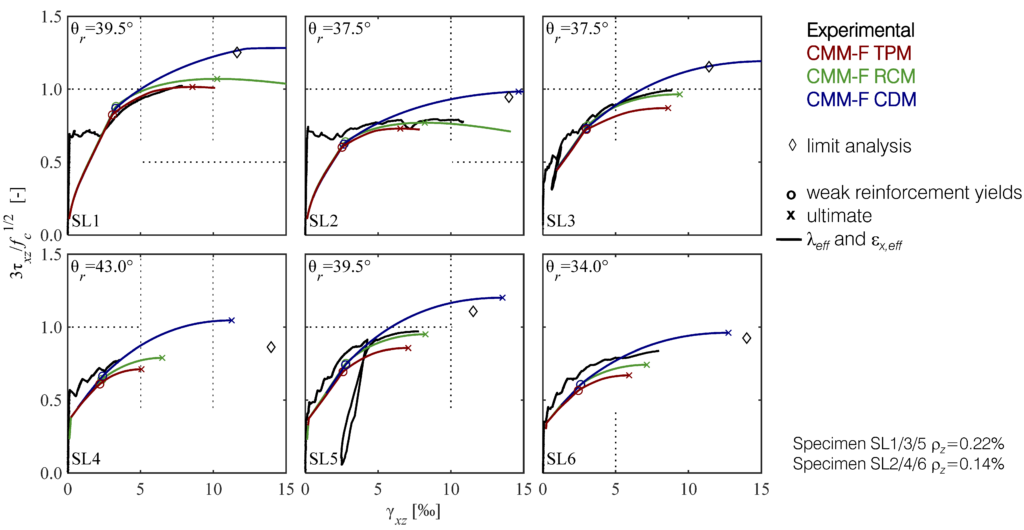
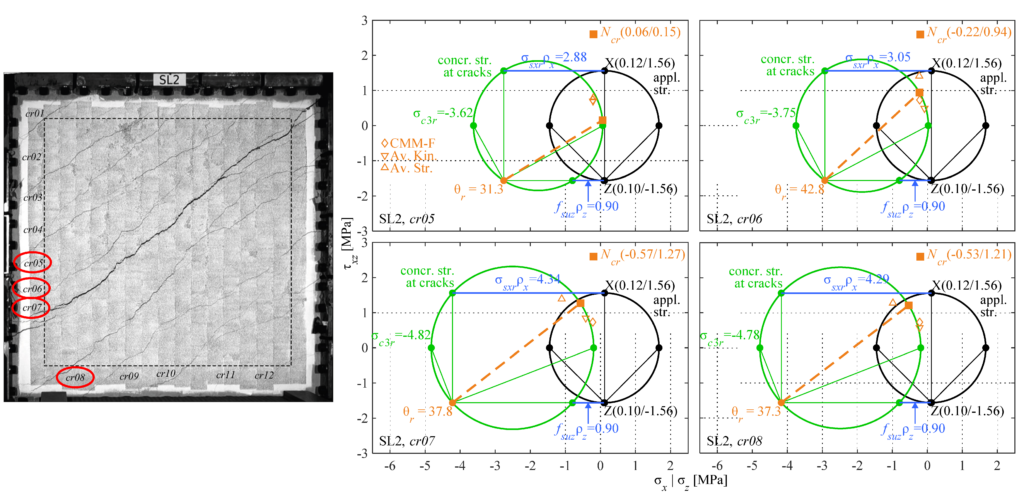
It could also be shown in the large-scale panel tests that the available aggregate interlock models from literature only work well in an average sense, as the model predictions of the SL tests were very good, but the aggregate interlock stresses calculated from the measured crack kinematics varied widely. Hence, the available aggregate interlock models are not suitable to predict the stress state of an arbitrarily shaped crack in a structural member. Additionally, crack spacings, inclinations and shapes are hardly predictable due to many local influences such as internal stress restraints, the variation of the tensile strength within the specimen, reinforcing bars running below the concrete cover and the distribution of aggregates in the concrete.
Alexander Beck