Link zur deutschen Version: Ein erster Schritt in Richtung KI-gestützte Fachwerkmodellgenerierung.
Strut-and-tie models are a widely applied approach to the design of reinforced concrete structures loaded in-plane such as beams or walls, at the level of approximation I. They are particularly suitable for geometric or load discontinuities. With the truss analogy, the force flow is shown with the struts representing concrete in compression and the ties representing reinforcement in tension. The classical stress field approach provides a more detailed design approach at the level of approximation II, which treats the force flow more continuously. A suitable stress field can be derived from a strut-and-tie model by considering nodal regions1Further extensions of the classical stress field approach might include elastic-plastic or non-linear constitutive laws and are often implemented in finite element models, such as the compatible stress field method, which is particularly suitable for existing structures.. Strut-and-tie models and stress fields are lower bound (static) solutions according to the theory of plasticity. Therefore, it is worth exploring different solutions during the design stage to obtain the closest one to the complete solution and to maximise the applicable load. They can also be used as plausibility checks for finite element analysis results to avoid modelling errors. However, the selection or suggestion of suitable strut-and-tie models is highly dependent on the expertise and experience of the design engineer and is a time-consuming and iterative process2For a more historical perspective on the development of truss models, please read this blog post.. This hinders the widespread use of strut-and-tie models that provide an interpretable and safe design. Digital tools such as machine learning could be used to bridge this gap. They could assist in achieving more consistent designs for reinforced concrete structures between different engineers and could ultimately be used for quality control and to reduce material usage. As a first step towards this goal, this article presents different attempts and their limitations of automated strut-and-tie model suggestions, followed by the research question and how a tool to validate strut-and-tie models with their corresponding stress fields helps to achieve our research goal.
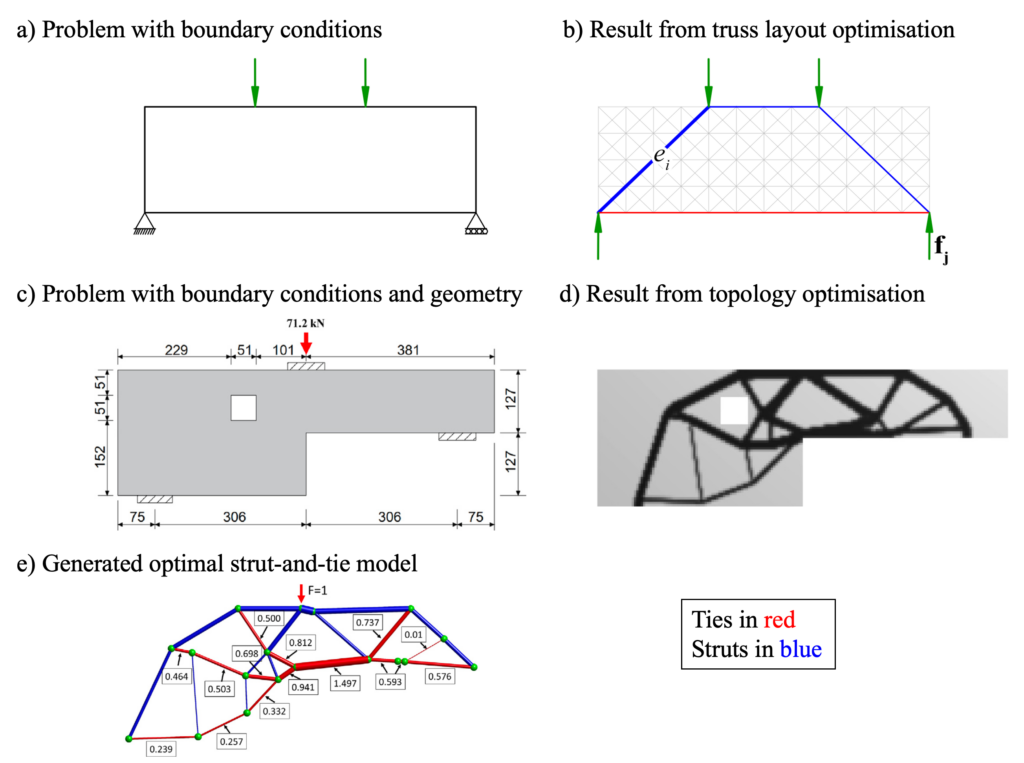
Various approaches have been developed for automated strut-and-tie model suggestion tools, primarily based on optimisation. The majority of these approaches can be categorised into two main groups: discrete (layout) optimisation and continuous optimisation. Discrete (layout) optimisation schemes, also known as truss layout optimisation, are based on a predefined grid or layout representing all possible nodes and edges of the resulting truss (see Figures 1a-b). Mathematical optimisation algorithms are applied to minimise a specific objective function, such as the total volume of reinforcing steel, within predefined constraints. This approach results in a regular pattern and it offers the flexibility to penalise inclined reinforcement to obtain a truss with only orthogonal reinforcement but still allow for inclined struts.
In contrast, continuous optimisation techniques often rely on topology optimisation. Topology optimisation typically aims to minimise the overall weight or volume of a structure through material removal while adhering to specific structural constraints, such as stress limits or deformations (see Figures 1c-d). It demands a high degree of geometric freedom and usually provides solutions based on linear elastic isotropic material behaviour, which speeds up the computations considerably. However, in the case of structural concrete, this simplification may not accurately represent the true material behaviour, as it neglects the influence of the reinforcement orientation, cracking, the different behaviour of reinforced concrete under tension and compression, and further material nonlinearities. Topology optimisation yields an intermediate result and is not yet the final strut-and-tie model (Figure 1d) with specific node locations and edges. Finding a suitable truss is difficult as one has to balance the constructability aspects (e.g., avoiding inclined reinforcement, or considering anchoring of the reinforcement) with the structural and material efficiency (Figure 1e).
To conclude, the discrete optimisation approach is often too rigid to capture complex geometries and offers little flexibility for user adjustments, while the continuous approach struggles to account for constructability aspects such as accommodating inclined reinforcement or very short ties. In addition, the issue of multiple load cases has been scarcely studied where for each load case a new strut-and-tie model needs to be defined. These challenges have led to a gap in the current strut-and-tie model generation methods. Few software applications have incorporated these optimisation-based approaches and they have not yet gained widespread adoption in practice. Moreover, the use of optimisation results in a single strut-and-tie model. However, the engineer needs design flexibility to consider other aspects unique to their structural problem and expertise, and the possibility to influence the resulting strut-and-tie model, as they remain the design maker at the end of the day. We want to address this research question in a data-driven but also domain-specific manner using machine learning tools by developing an AI-assisted automated strut-and-tie model generation tool. This tool does not solely focus on generating the most optimal strut-and-tie model but instead suggests a range of suitable strut-and-tie models and therefore also allows for an interplay between the user and the machine to assist the engineer in the decision-making process.
As a first step towards this goal and for a reliable data generation pipeline, we need a validation tool to verify the proposed strut-and-tie models. The pipeline is needed to train and test the final machine learning model, and validate the final suggestions. Focusing on the ultimate limit state, this tool does not only check force equilibrium but also the stress fields and their nodal regions to achieve a more refined design at the level of approximation II.
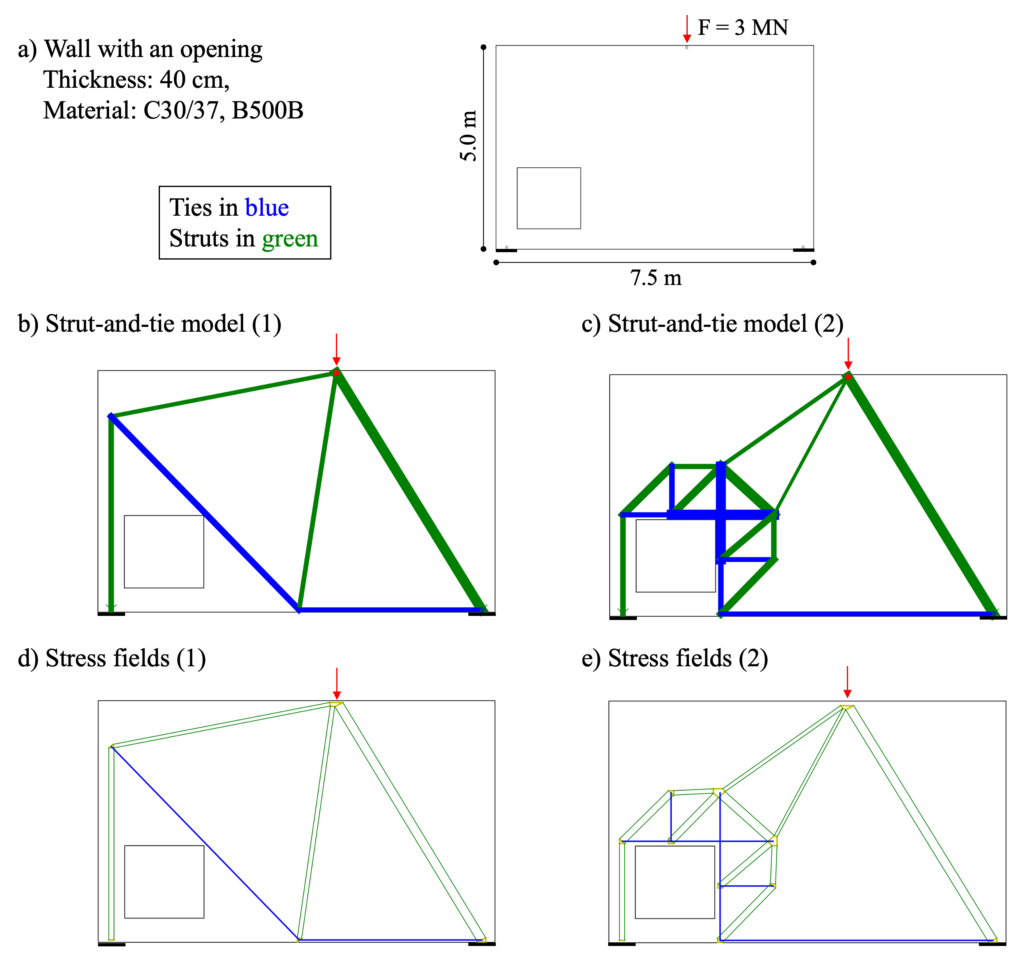
Using the example of a wall with an opening (see Figure 2a, example from Schlaich et al. 1987) and two different corresponding strut-and-tie models3The right concentrated strut is a simplification and one should place transverse reinforcement for spreading the forces., we aim to demonstrate the need for generating multiple strut-and-tie models. The first model (Figure 2b) illustrates a simple yet efficient strut-and-tie model that uses inclined reinforcement and has a low overall steel consumption. Without considering minimum reinforcement, anchoring of the reinforcement, and other constructability issues, the total steel volume is approximately 0.021 m3. The second model (Figure 2c) shows a more regular strut-and-tie model with only orthogonal reinforcement. However, this model uses approximately 70% more steel, resulting in a total steel volume of 0.036 m3. Nonetheless, one should not draw premature conclusions.
The safe application of strut-and-tie models requires the fulfilment of the underlying assumptions of the theory of plasticity, including ductility. Providing sufficient minimum reinforcement, e.g., here 12@150, is non-negotiable. As strut-and-tie models are based on linear elastic material behaviour, they can be superimposed. By considering the minimum reinforcement, the load-bearing capacity of the second strut-and-tie model could be utilised by about 9%. This decreases in combination the load for the first model, ultimately leading to an overall reduction in the steel volume of about 10%. There are of course other possible allocations, e.g., Schlaich et al. propose to have each model carry half of the load. This example demonstrates that it is optional to consider just one optimal strut-and-tie model; instead, several can be combined to take advantage of each model.
The validation tool shows the equivalent stress fields in Figures 2d and e, assuming an anchoring of the reinforcement outside the nodal zone and hydrostatic nodes. It indicates whether enough concrete can be activated in the nodes and makes therefore critical areas more evident to the user.
In conclusion, this example illustrates the trade-off between a simpler strut-and-tie model (1), which optimizes steel usage but may compromise constructability, and a more regular strut-and-tie model (2) with higher steel usage but easier construction.
As a next step, we explore different machine learning tools to tackle the problem of AI-assisted automated strut-and-tie model generation. However, this will be the topic for a future blog post. In the meantime, feel free to reach out to Karin Yu if you have any suggestions or comments.
Karin Yu