Ein erster Schritt in Richtung KI-gestützte Fachwerkmodellgenerierung – Concrete E-Learning Platform

Link to the English version: A first step towards AI-assisted strut-and-tie model generation.

Fachwerkmodelle sind ein weit verbreiteter Ansatz zur Bemessung von in der Ebene belasteten Stahlbetontragwerken wie Balken oder Wände auf der Näherungsstufe 1. Sie sind insbesondere für geometrische oder Lastdiskontinuitäten geeignet. Mit der Fachwerkanalogie wird der Kraftfluss dargestellt, in welchem Druckstreben den Beton unter Druck und Zugstreben die Bewehrung unter Zug repräsentieren. Klassische Spannungsfelder bieten einen detaillierteren Bemessungsansatz auf der Näherungsstufe 2 an, der den Kraftfluss kontinuierlicher betrachtet. Geeignete Spannungsfelder kann man durch Berücksichtigung der Knotenbereiche aus einem Fachwerkmodell ableiten¹. Fachwerkmodelle und Spannungsfelder sind Lösungen nach dem unteren Grenzwertsatz der Plastizitätstheorie. Demnach lohnt es sich während der Entwurfsphase verschiedene Lösungen zu untersuchen, um diejenige zu finden, die der vollständigen Lösung am nächsten kommt, und um die zulässige Last zu maximieren. Ausserdem können sie als Plausibilitätsüberprüfung der Ergebnisse aus Finite-Element-Analysen dienen, um Modellierungsfehler zu vermeiden. Die Auswahl oder der Vorschlag geeigneter Fachwerkmodelle ist einerseits stark von der Expertise und der Erfahrung des:der Bauingenieur:in abhängig und andererseits ein zeitintensives und iteratives Verfahren². Diese Punkte erschweren den breiten Einsatz von Fachwerkmodellen, welche eine interpretierbare und sichere Bemessung ermöglichen. Digitale Hilfsmittel, wie maschinelles Lernen, könnten diese Lücke schliessen. Sie könnten dazu beitragen, dass unterschiedliche Ingenineur:innen einheitlichere Entwürfe für Stahlbetonkonstruktionen erstellen, und könnten letztlich zur Qualitätskontrolle und Materialreduktion eingesetzt werden. Als erster Schritt in diese Richtung stellt dieser Artikel verschiedene Ansätze von Fachwerkmodellgenerierungsmethoden und ihre Grenzen vor, gefolgt von unserer Forschungsfrage und wie ein Hilfsmittel zur Validierung von Fachwerkmodellen uns beim Erreichen unserers Forschungsziels hilft.

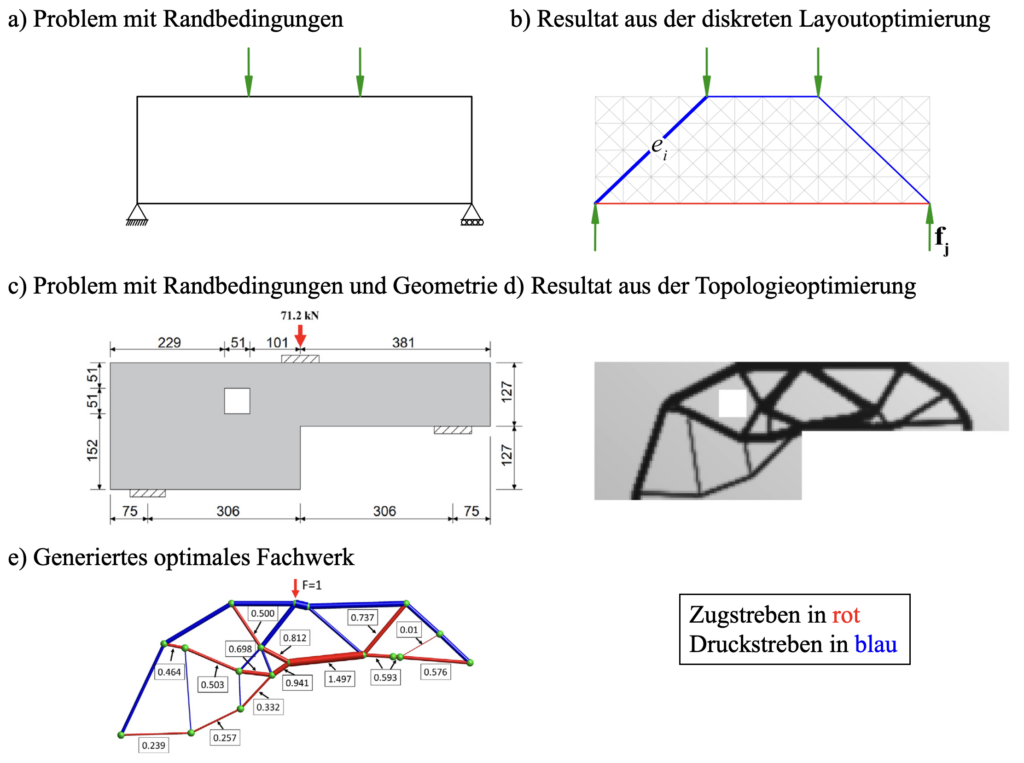
Abbildung 1: Beispiele von Fachwerkmodellgenerierungsansätzen, a-b) für diskrete Layoutoptimierung [Bildquelle: Mozaffari et al. 2020], c-e) für kontinuierliche Optimierung [Bildquelle: Xia et al. 2020].

Verschiedene Ansätze wurden zur automatisierten Generierung von Fachwerkmodellen entwickelt, welche grösstenteils auf Optimierungsalgorithmen basieren. Die Mehrheit dieser Ansätze können in die folgende zwei Kategorien unterteilt werden: diskrete (Layout-) oder kontinuierliche Optimierung. Diskrete (Layout-)Optimierungsverfahren basieren auf einem vordefinierten Gitter oder Layout, das alle möglichen Knoten und Kanten des resultierenden Fachwerks darstellt (siehe Abbildung 1a-b). Mathematische Optimierungsalgorithmen werden verwendet, um eine Zielfunktion, wie z.B. das Gesamtstahlvolumen, unter vordefinierten Bedingungen zu minimieren. Aus der diskreten Optimierung erhält man ein regelmässiges Muster, wo man auch schiefe Bewehrungen pönalisieren kann, damit man ein Fachwerk mit nur orthogonaler Bewehrung erhält, aber dennoch schräge Druckstreben erlaubt.

Im Gegensatz dazu basieren kontinuierliche Optimierungsverfahren oft auf der Topologieoptimierung. Die Topologieoptimierung zielt in der Regel auf die Minimierung des Gesamtgewichts oder Volumens einer Struktur unter bestimmten strukturellen Bedingungen, wie z.B. Spannungsgrenzen oder Verformungen, indem Material entfernt wird (siehe Abbildungen 1c-d). Sie erfordert grosse geometrische Freiheiten und liefert meistens Ergebnisse basierend auf einem linear elastischen, isotropen Materialverhalten, was die Berechnungen erheblich beschleunigt. Im Falle von Stahlbeton, entspricht diese vereinfachende Annahme aber nicht dem wahren Materialverhalten, da sie den Einfluss der Bewehrungsrichtung, der Rissbildung, das unterschiedliche Materialverhalten unter Zug und Druck und andere materielle Nichtlinearitäten vernachlässigt. Die Topologieoptimierung liefert nur ein Zwischenresultat und noch nicht das finale Fachwerk (Abbildung 1d) mit spezifischen Knotenpunkten und Streben. Es ist schwierig, ein geeignetes Fachwerk zu finden, da man die Aspekte der Bauausführung (z.B. Vermeidung von schiefer Bewehrung oder die Berücksichtigung der Bewehrungsverankerung) gegenüber der strukturellen und materiellen Ausnutzung abwägen muss (Abbildung 1e).

Zusammenfassend lässt sich sagen, dass der diskrete Optimierungsansatz oft zu rigide ist, um komplexe Geometrien zu erfassen, und wenig Flexibilität für Anpassungen durch den:die Benutzer:in anbietet, während der kontinuierliche Ansatz Schwierigkeiten hat, Aspekte der Bauausführung, wie schiefe Bewehrungen oder kurze Zugstreben, zu berücksichtigen. Ausserdem wurde das Problem von mehreren verschiedenen Lastfällen, wo man für jeden einzelnen Lastfall wieder ein neues Fachwerkmodell definieren müsste, wenig erforscht. Diese Herausforderungen haben zu einer Lücke in den derzeitigen Fachwerkmodellgenerierungsmethoden geführt. Wenige kommerzielle Programme beinhalten diese optimierungsbasierten Ansätze und sie haben sich in der Praxis noch nicht durchgesetzt. Des Weiteren führen Optimierungen nur zu einem einzelnen Fachwerkmodell. Jedoch benötigt der:die Ingenieur:in Freiheiten, um andere problemspezifische und erfahrungsbasierte Aspekte zu berücksichtigen, und auch die Möglichkeit das resultierende Fachwerk zu beeinflussen, da er:sie am Ende des Tages der:die Entscheidungsträger:in bleibt. Wir möchten diese Forschungsfrage auf eine datenbasierte und domänenspezifische Weise mit Hilfe von maschinellem Lernen angehen, indem wir ein KI-gestütztes automatisiertes Fachwerkmodellgenerierungstool entwickeln. Dieses Tool konzentriert sich nicht nur auf die Generierung eines optimalen Fachwerks, sondern schlägt eine Auswahl von Fachwerkmodellen vor und erlaubt ein Zusammenspiel zwischen Benutzer:in und Maschine, um den:die Ingenieur:in im Entscheidungsprozess zu unterstützen.

Als ersten Schritt in Richtung dieses Ziels und für eine zuverlässige Datengenerierungspipeline, benötigen wir ein Validierungstool zur Überprüfung der vorgeschlagenen Fachwerke. Eine solche Pipeline wird für das Training und Testen des maschinellen Lernmodells benötigt, und um die endgültigen Vorschläge zu validieren. Dieses Tool, das derzeit nur die Traglast berücksichtigt, überprüft nicht nur das Kräftegleichgewicht, sondern auch die Spannungsfelder und Knotenbereiche, um eine verfeinerte Bemessung auf Näherungsstufe 2 zu erreichen.

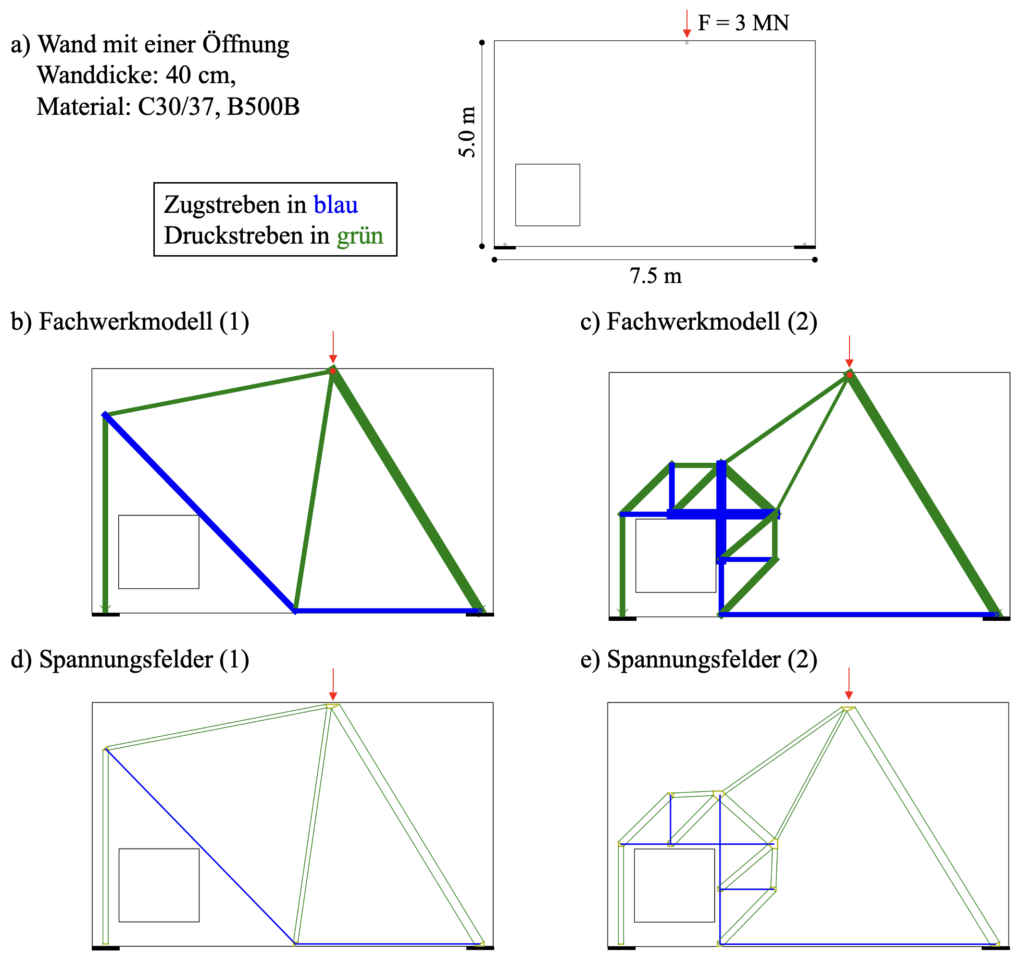
**Abbildung 2: Beispiel einer Wand mit einer Öffnung in a), für zwei Fachwerke (b und c) und den vom Validierungstool generierten entsprechenden Spannungsfeldern (d und e).**

Anhand des Beispiels einer Wand mit einer Öffnung (siehe Abbildung 2a, Beispiel aus Schlaich et al. 1987) und zwei verschiedenen entsprechenden Fachwerken³, möchten wir die Notwendigkeit für die Generierung mehrerer Fachwerke aufzeigen. Das erste Modell (Abbildung 2b) veranschaulicht ein einfaches aber effizientes Fachwerk, das schiefe Bewehrung verwendet und einen geringen Gesamtstahlverbrauch aufweist. Ohne die Mindestbewehrung, die Verankerung der Bewehrung und andere konstruktive Details zu berücksichtigen, beträgt das Gesamtstahlvolumen 0.021 m³. Das zweite Modell (Abbildung 2c) zeigt ein regelmässigeres Fachwerk mit nur orthogonaler Bewehrung. Allerdings benötigt dieses Modell 70% mehr Stahl und zwar 0.036 m³. Dennoch sollte man keine voreiligen Schlüsse ziehen.

Die sichere Anwendung von Fachwerken setzt die Erfüllung der zugrunde liegenden Annahmen der Plastizitätstheorie, einschliesslich der Duktilität, voraus. Eine ausreichende Mindestbewehrung, z.B. hier 12@150 ist unumgänglich. Da die Fachwerkmodelle auf linear elastischem Materialverhalten basieren, können diese superponiert werden. Durch die Verwendung der Mindestbewehrung, kann die Traglast des zweiten Fachwerkmodells um 9% ausgenutzt werden. Dies verringert in Kombination die Last des ersten Modells, sodass dies zu einer Reduktion des Stahlvolumens um 10% führt. Es gibt selbstverständlich andere mögliche Aufteilungen. Schlaich et al. schlagen z.B. vor, dass jedes Modell die Hälfte der Last trägt. Dieses Beispiel zeigt, dass es optional ist, nur ein Fachwerk zu betrachten; stattdessen können mehrere kombiniert werden, um die Vorteile jedes Modells auszunutzen.

Das Validierungstool liefert uns die äquivalenten Spannungsfelder in den Abbildungen 2d und e, unter der Annahme einer Verankerung der Bewehrung ausserhalb der Knotenbereiche und hydrostatische Knoten. Es zeigt, ob genug Beton aktiviert werden kann und macht somit kritische Bereiche für den:die Benutzer:in ersichtlicher.

Dieses Beispiel veranschaulicht die Abwägung zwischen einem simplerem Fachwerk (1), das den Stahlverbrauch optimiert, aber die Bauausführung beeinträchtigen kann, und einem regelmässigeren Fachwerk (2) mit einem höheren Stahlverbrauch aber dafür einer einfacheren Bauweise.

Als nächsten Schritt untersuchen wir verschiedene Algorithmen und Methoden des maschinellen Lernens, um unser Problem der KI-gestützten automatischen Generierung von Fachwerkmodellen anzugehen. Dies wird jedoch ein Thema für einen zukünftigen Blogbeitrag sein. In der Zwischenzeit können Sie sich gerne an Karin Yu wenden, wenn Sie Vorschläge oder Bemerkungen haben.

Karin Yu