Link to English version: Gaining Insights into a Mechanical Model with Decision Trees
In diesem Blogbeitrag möchte ich zeigen, wie ich Entscheidungsbäume genutzt habe, um Einblick in ein bestehendes Modell zu gewinnen.
Dieser Blog enthält bereits mehrere Beiträge zu Anwendungen der künstlichen Intelligenz (KI) und, spezifischer, des maschinellen Lernens (ML) im Bauingenieurwesen (KI-gestützte Tragwerksplanung, KI-gestützte Fachwerkmodellgenerierung, eine Kombination aus ML und Finiten-Elemente-Analyse und die Nutzung von neuronalen Netzen in der direkten Steifigkeitsmethode). Dieser Beitrag stellt eine vergleichsweise einfache Anwendung vor, die sich an Lesende ohne vorgängige Erfahrung im maschinellen Lernen richtet.
Einer der Hauptvorteile der Entscheidungsbäume ist, dass sie auch ohne viel Erfahrung im Programmieren und ohne Vorwissen zum maschinellen Lerne relativ einfach zu implementieren sind. Dadurch sind sie besonders gut als Einstieg ins maschinelle Lernen geeignet. Gleichzeitig sind die Resultate einfach zu interpretieren, da sie als intuitiv verständliches Baumdiagramm dargestellt werden können. In diesem Beitrag benutze ich diese Eigenschaft der Entscheidungsbäume um ein bestehendes Modell besser zu verstehen, im Anwendungsbeispiel ein mechanisches Modell, das die Tragfähigkeit eines zweifeldrigen Plattenstreifens aus Stahlbeton berechnet.
Hintergrundwissen
Das maschinelle Lernen, ein Teilgebiet der künstlichen Intelligenz, umfasst verschiedene Methoden zur Beschreibung und zum Lernen aus grossen Datenmengen. Um ihrem größten Nachteil entgegenzuwirken, nämlich, dass man nicht nachvollziehen kann, wie und warum der ML-Algorithmus zu einem bestimmten Ergebnis kommt (Black-Box-Modell), wird seit kurzem im Bereich der Ingenieurwissenschaften die erklärbare KI erforscht. Bei erklärbaren KI-Algorithmen können Vorhersagen auf ihre Plausibilität und Genauigkeit hin beurteilt oder sogar mit Fachwissen nachvollzogen werden. Eine umfassende Übersicht über erklärbare KI findet sich in diesem Open-Source Paper.
Einer der einfachsten und am besten erklärbaren Algorithmen im maschinellen Lernen ist der (Klassifizierungs-)Entscheidungsbaum. Der Entscheidungsbaum lernt einen Wert (oft die Klasse “ja” oder “nein”) vorherzusagen, indem er die Eingabedaten auf der Grundlage bestimmter Eingabeparameter (der Merkmale) sukzessive aufteilt.
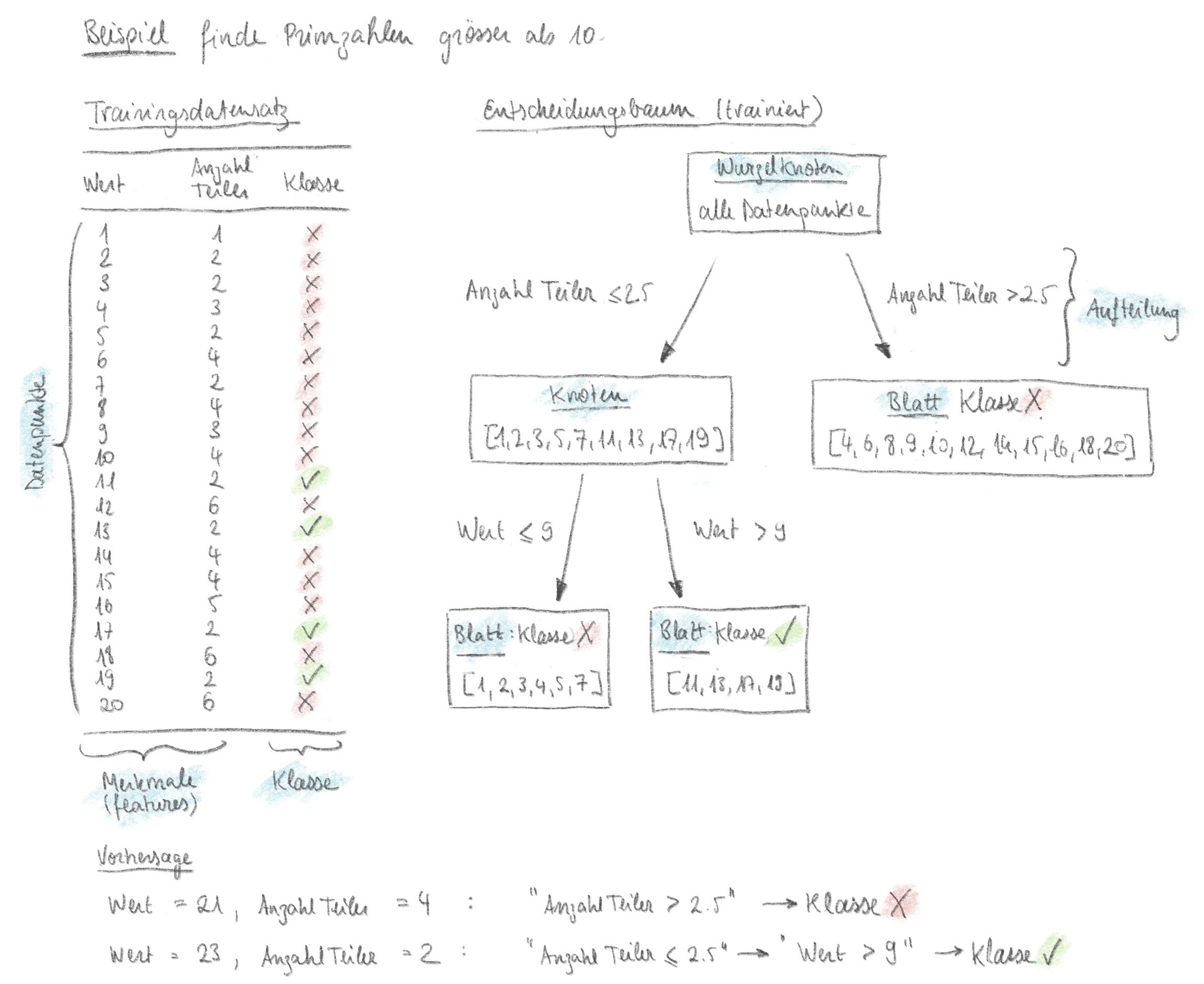
Der Entscheidungsprozess kann als Baum dargestellt werden, der sich bei jeder Aufteilung verzweigt. Da jeder Aufteilungsschritt durch Benutzende bewertet werden kann, ist das Ergebnis des Modells sehr gut erklärbar. Abbildung 1 zeigt das Beispiel eines Entscheidungsbaums, der Zahlen in die Klassen “Primzahl > 10” und “keine Primzahl > 10” einteilt, wobei die Merkmale «Wert» und «Anzahl Teiler» jeder Zahl im Datensatz zur Verfügung stehen. Beim Training mit dem Datensatz auf der linken Seite in Abbildung 1 sucht der Algorithmus die beste Aufteilung. Der trainierte Entscheidungsbaum (rechte Seite in Abbildung 1) kann dann genutzt werden um die Klasse von neuen Datenpunkten vorherzusagen. Das Jupyter Notebook mit dem Code dieses Beispiels befindet sich in diesem Github-Repository.
Anwendungsbeispiel
Das folgende Beispiel zeigt, wie ein Entscheidungsbaum verwendet werden kann, um Einblick in ein bestehendes mechanisches Modell zu erhalten. Der Schwerpunkt liegt nicht, wie üblich und im vorigen einfachen Beispiel gezeigt, auf der Suche nach dem genauesten Klassifizierungsmodell zur Vorhersage der Klasse neuer Daten, sondern darauf zu verstehen, mit welchen Aufteilungen der Entscheidungsbaum zum Ergebnis gelangt. Dies kann helfen zu verstehen, welche Parameter für das Ergebnis des mechanischen Modells am wichtigsten sind.
Im Anwendungsbeispiel wird ein bestehendes mechanisches Modell für einen zweifeldrigen Plattenstreifen aus Stahlbeton (Abbildung 2) verwendet. Das mit Grossversuchen validierte mechanische Modell berechnet die nichtlineare Reaktion des Plattenstreifens und kann seine Tragfähigkeit vorhersagen, wobei das begrenzte Verformungsvermögen der verwendeten Materialien berücksichtigt wird. Es ist von Interesse, welche Parameterkombinationen zu einer Tragfähigkeit führen, die grösser als die nach der Plastizitätstheorie berechnete Traglast ist1Es ist möglich mit dem mechanischen Modell Tragfähigkeiten (als Last bei Versagen) höher als die plastische Traglast zu finden, da das mechanische Modell die Verfestigung der Bewehrung berücksichtigt, während die Traglast nach Plastizitätstheorie mit der Fliessgrenze des Stahls berechnet wird.. Das bedeutet, dass die verwendeten Materialien in dieser Konfiguration ein ausreichend großes Verformungsvermögen haben, um vereinfachte Berechnungsmethoden nach der Plastizitätstheorie sicher anwenden zu können. Mehr Hintergrundinformationen dazu sind zum Beispiel in diesem Blogbeitrag.
Der Entscheidungsbaum wird so trainiert, dass er die Klasse “ok” vorhersagt, wenn die mit dem nichtlinearen mechanischen Modell berechnete Tragfähigkeit die plastische Traglast überschreitet (Qu/Qpl > 1), und andernfalls “not ok”.

Erstellung des Datensatzes
Indem das mechanische Modell viele Male mit verschiedenen Eingabewerten ausgeführt wird, kann ein Datensatz erzeugt werden. Die Wahl der richtigen Merkmale, ist einer der wichtigsten Schritte bei der Datenerzeugung. Der Datensatz könnte wie folgt aussehen:
| fs [MPa] | k [-] | εsu [-] | c [-] | ρs [%] | L [m] | fc [MPa] | Klasse |
|---|---|---|---|---|---|---|---|
| 496 | 1.09 | 0.087 | 0.11 | 0.78 | 4.37 | 54.1 | ok |
| 505 | 1.13 | 0.026 | 0.06 | 2.94 | 4.53 | 41.7 | not ok |
| 483 | 1.13 | 0.092 | 0.25 | 0.51 | 7.12 | 36.4 | ok |
| 517 | 1.07 | 0.082 | 0.08 | 0.88 | 4.37 | 57.8 | ok |
| 491 | 1.11 | 0.081 | 0.18 | 1.74 | 6.61 | 29.0 | not ok |
| … | … | … | … | … | … | … | … |
Bezeichnungen
fs: Fliessgrenze der Bewehrung
k: Verfestigungsmodul der Bewehrung (k = fs/ft, wobei ft = Zugfestigkeit der Bewehrung)
εsu: Dehnung der Bewehrung bei Erreichen der Zugfestigkeit
c: “Ausrundung” des Materialgesetzes der Bewehrung , siehe Parameter c3 in “S. Haefliger, K. Thoma, and W. Kaufmann, ‘Influence of a triaxial stress state on the load-deformation behaviour of axisymmetrically corroded reinforcing bars’, Construction and Building Materials, vol. 407 (Link)
ρs: Bewehrungsgehalt beim Zwischenauflager (der Bewehrungsgehalt im Feld wird entsprechend der elastischen Biegemomentenlinie berechnet)
L: Spannweite
fc: Druckfestigkeit des Beton
Es sollte darauf geachtet werden, das Problem so zu formulieren, dass die Klassen ausgewogen sind, d. h. dass es eine annähernd gleiche Anzahl von Daten pro Klasse gibt, da der Algorithmus sonst dazu neigt, die grösseren Klassen zu bevorzugen.
Erstellen des Entscheidungsbaums
Der Entscheidungsbaum kann zum Beispiel mit einer Implementierung aus der Open-Source Python Bibliothek scikit-learn erstellt werden. Wichtige Parameter (im maschinellen Lernen Hyperparameter genannt) sind die maximale Tiefe des Baums und die Mindestanzahl von Datenpunkten pro Split (Zwischenknoten) oder pro Blatt (Endknoten). Diese Hyperparameter helfen eine Überanpassung (Overfitting) der Daten zu verhindern, wie später erläutert wird.
Training
Der Trainingsprozess beginnt mit dem Wurzelknoten, der den gesamten Datensatz enthält. Die Daten werden dann z. B. anhand des Gini-Unreinheitskriteriums aufgeteilt. Für verschiedene mögliche Merkmale und Teilungswerte berechnet der Algorithmus die Gini-Unreinheit, um die Teilung zu finden, die die Unreinheit am besten minimiert. Anders ausgedrückt werden das Merkmal und der Wert ermittelt, die die Daten am besten in reine Teilmengen aufteilen. Der Algorithmus erstellt so eine neue Ebene mit Knoten und wechselt zu dieser.
Dieser Vorgang wird so lange wiederholt, bis die maximale Baumtiefe erreicht ist oder die Anzahl der Datenpunkte in einem Knoten zu gering ist, um eine weitere Aufteilung vorzunehmen (d. h. die Mindestanzahl der Werte pro Blatt ist erreicht). Die Genauigkeit des Entscheidungsbaums wird dann bewertet, um sicherzustellen, dass die Vorhersagen genau genug für die Interpretation sind. Dieser Artikel gibt einen Überblick über die Methoden zur Bewertung von Entscheidungsbäumen.
Interpretation der Resultate
Am einfachsten lassen sich die Ergebnisse mit Hilfe einer grafischen Darstellung des Baums interpretieren, wie z. B. mit der in scikit-learn enthaltenen Funktion oder mit dtreeviz. Dies ist natürlich nur bis zu einer bestimmten Baumtiefe möglich, danach wird es unhandlich. Abbildung 3 zeigt ein Beispiel für einen Baum mit Tiefe 3, wobei für dieses Anwendungsbeispiel auch Entscheidungsbäume mit unterschiedlichen Hyperparametern, die auf demselben Datensatz trainiert wurden, analysiert wurden.
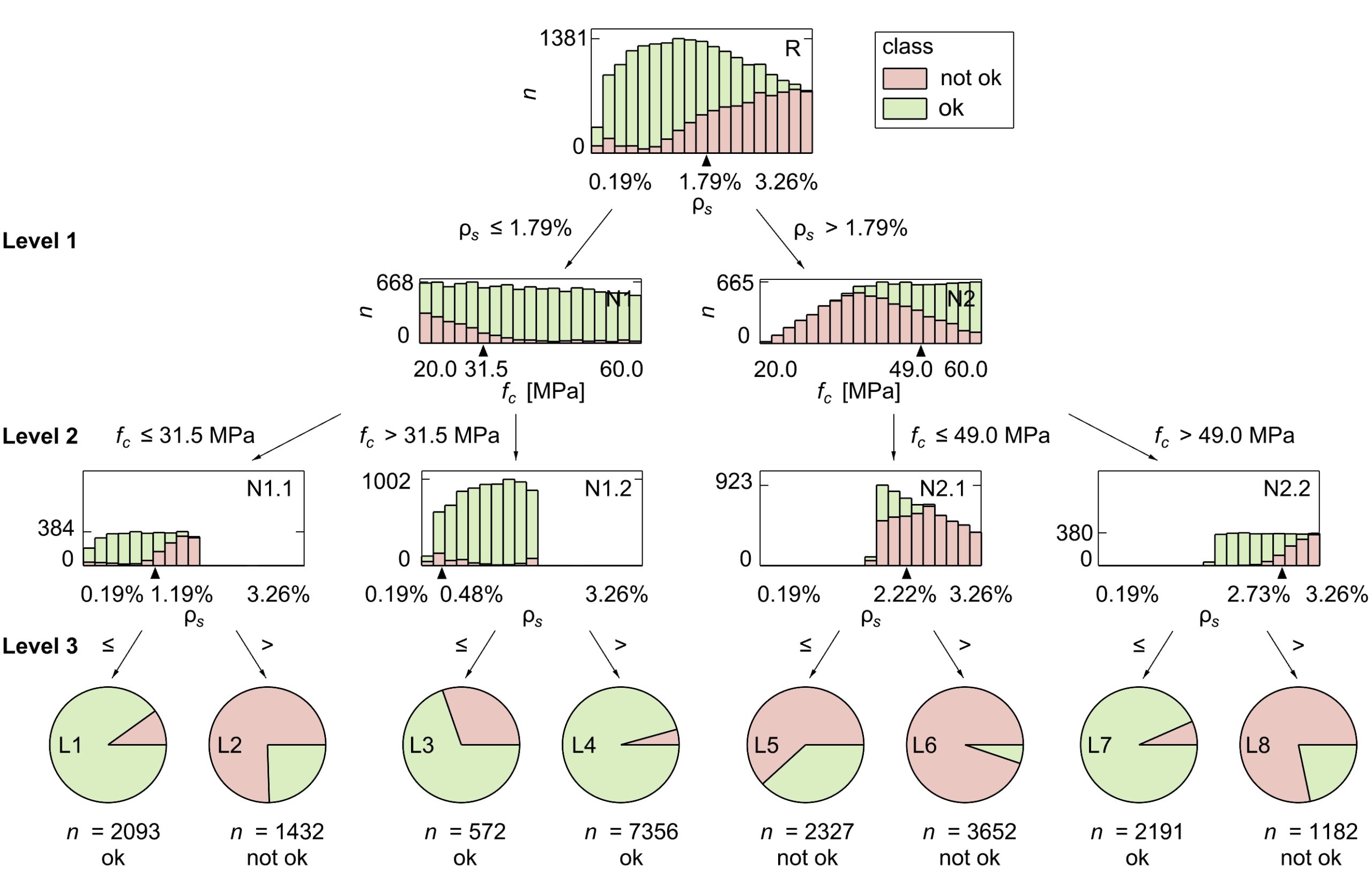
Die Aufteilungen im resultierenden Baum können mit Fachwissen interpretiert werden. Im Anwendungsbeispiel ist die erste Aufteilung immer (d. h. für alle analysierten Baumtiefen) bei einem Bewehrungsgehalt von etwa 1,8 % (siehe Abbildung 3, Level 1). Dies deutet auf einen aussagekräftigen Zusammenhang innerhalb der Daten hin.
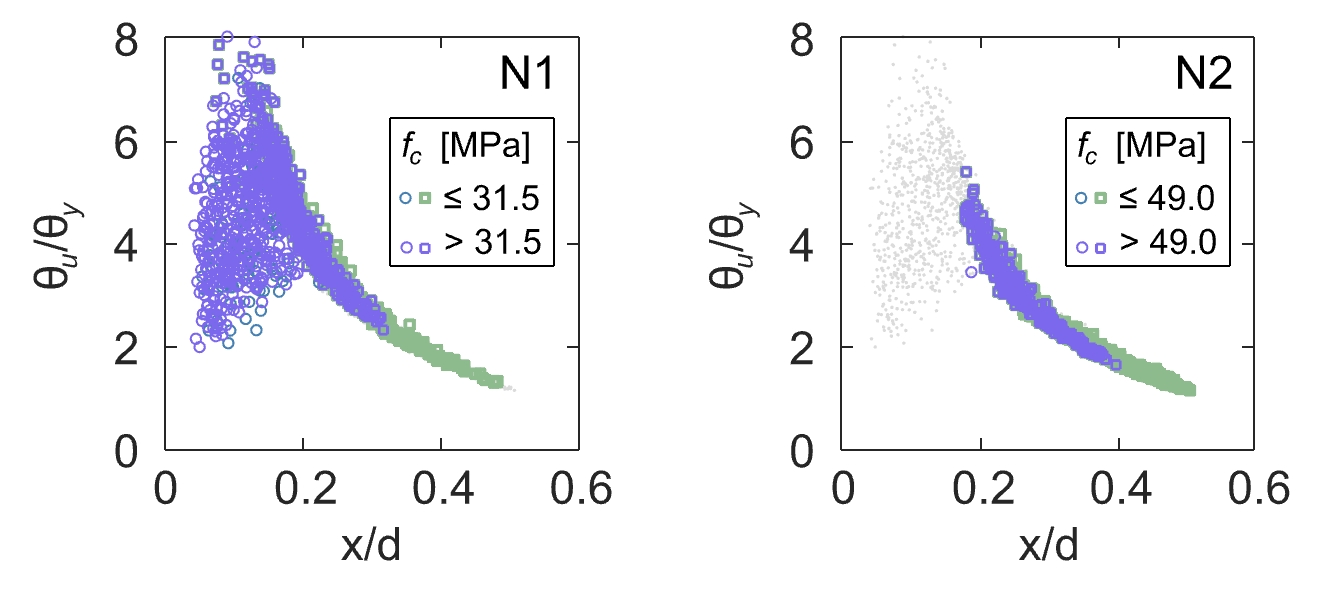
Dieser Zusammenhang kann mit Hintergrundinformationen zu den Versagenskriterien in jedem Schnitt des mechanischen Modells interpretiert werden. Der Querschnitt kann entweder durch Bruch der Bewehrung versagen oder wenn der Beton in der Druckzone eine festgelegte Dehnung erreicht, die ein Versagen durch Betonbruch anzeigt. In Anlehnung an die grafische Darstellung, in diesem Blogbeitrag, wird deutlich, dass der Algorithmus die Daten nach der Versagensart trennt, siehe Abbildung 4. Dies ist bemerkenswert, wenn man bedenkt, dass die Daten keine Informationen über die Versagensart enthalten (siehe Tabelle 1) und spricht für deren Bedeutung im mechanischen Modell.
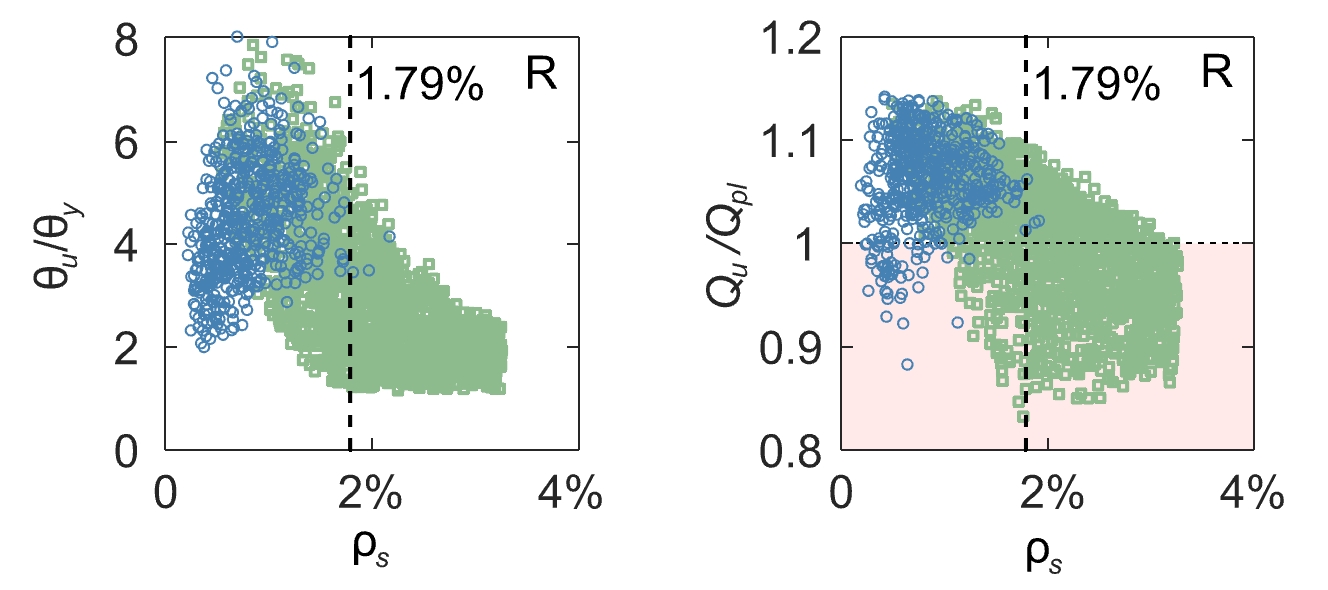
Die zweite Ebene der Unterteilungen (Abbildung 3) ist etwas weniger intuitiv, da keines der Versagenskriterien direkt von der Betondruckfestigkeit fc abhängt2Versagen durch Reissen der Bewehrung falls die Dehnung der Bewehrung in einem Schnitt grösser ist als die Bruchdehnung εsu. Versagen durch Betonbruch falls die mittlere Betondehnung am Rand des Querschnitts 5‰ überschreitet, unabhängig von der Betondruckfestigkeit.. Wenn man die Daten mit dem mechanischen Bewehrungsgrad ω auf der Abszisse aufträgt, ergibt sich ein klareres Bild. Die Betondruckfestigkeit ist Teil der Definition des mechanischen Bewehrungsgehaltes.
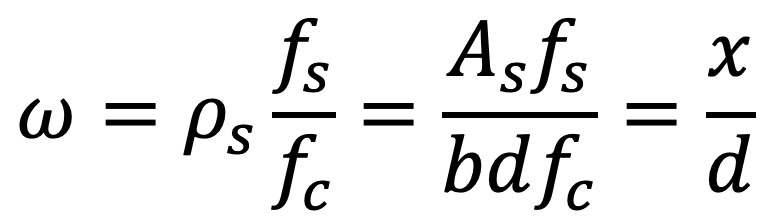
Notationen
ω: mechanischer Bewehrungsgehalt
ρs: Bewehrungsgehalt
fs: Fliessgrenze der Bewehrung
fc: Betondruckfestigkeit
As: Querschnittsfläche der Bewehrung
b: Querschnittsbreite
d: statische Höhe
x: Distanz zur neutralen Achse / Höhe der Betondruckzone
Es ist bekannt, dass dieses Verhältnis einen erheblichen Einfluss auf die Duktilität von Bauwerken hat. Es ist in den schweizerischen und europäischen Normen mit der Bedingung x/d < 0.35 enthalten, die erfüllt sein muss, um plastische Methoden bei der Bemessung anwenden zu dürfen. Interpretiert man die Aufteilung auf Ebene 2 des Entscheidungsbaums aus mechanischer Sicht, so verringert eine hohe Betondruckfestigkeit die Druckzonenhöhe x, was Reissen der Bewehrung als Versagensmechanismus und große Rotationen beim Versagen θu (d.h. hohe Duktilität) begünstigt.
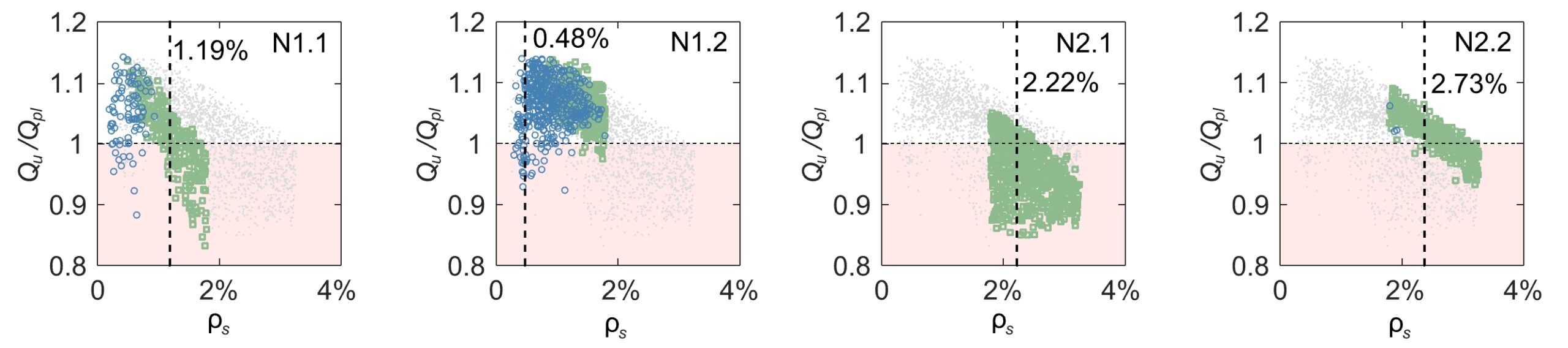
Eine hohe Betondruckfestigkeit fc hält das Verhältnis niedrig, und je höher der Bewehrungsgehalt ρs, desto höher muss fc sein, um dem entgegenzuwirken. Dies könnte die unterschiedlichen Aufteilungswerte fc = 31.5 MPa und fc = 49.0 MPa an den Abzweigungen der Stufe 2 erklären, siehe Abbildung 3 und Abbildung 5.
Auf Ebene 3 (siehe Abbildung 3 und Abbildung 6) sind die Daten wieder entlang des Bewehrungsgehalts ρs aufgeteilt, was die Annahme bestätigt, dass dies eine der wichtigsten Bemessungsvariablen ist. Es ist jedoch nicht üblich, dass alle Knoten auf der gleichen Ebene entlang der gleichen Variablen aufgeteilt sind. Bei der Interpretation ist es auch wichtig zu berücksichtigen, wie genau das Modell die Daten aufteilen kann. Bei der Vorhersage der Daten in Blatt L5 liegt der Entscheidungsbaum bei fast 40% des Trainingsdatensatzes falsch, siehe Abbildung 3. Aus der Aufteilung in Knoten N2.1 folgt also, dass die Klasse bei ρs > 2.22% relativ sicher «not ok» ist, und bei ρs < 2.22% eine weitere Baumebene helfen würde die Daten treffender aufzuteilen.
Zusammenfassend hat die Analyse der verschiedenen Aufteilungen im Entscheidungsbaum (i) dazu beigetragen, einen Einblick in die wichtigsten Merkmale zu gewinnen, und (ii) einen Anreiz geschaffen, die Beziehung zwischen diesen Merkmalen und bekannten mechanischen Prinzipien aufzudecken.
Anwendungsgrenzen
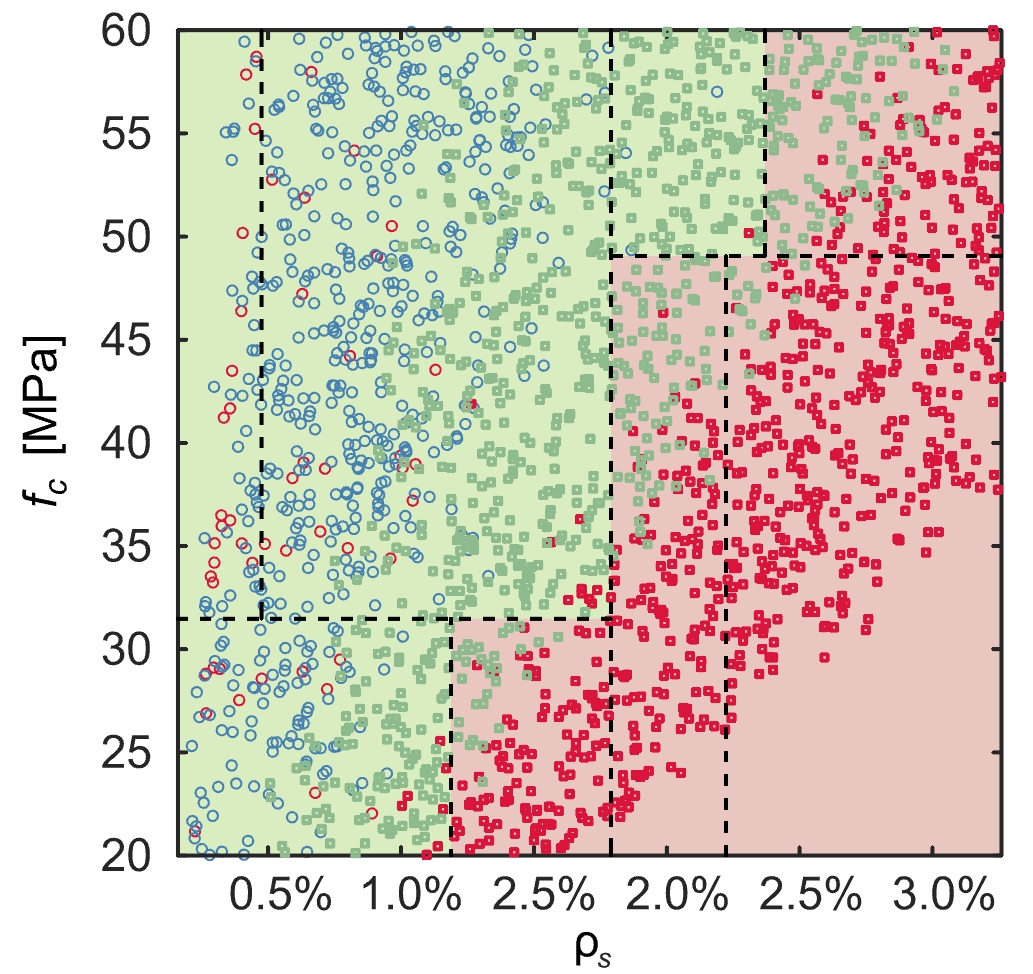
Wie bereits erwähnt, sind die Ergebnisse nur bis zu einer bestimmten Baumtiefe leicht interpretierbar, was die Anwendbarkeit für sehr komplexe Probleme einschränkt. Der Ansatz ist nur für (eine) kategorische Frage mit wenigen Antworten einfach, wie im Anwendungsbeispiel zu sehen. Darüber hinaus kann die Tatsache, dass der Entscheidungsbaum den Datensatz je Knoten nur entlang eines Merkmales aufteilen kann (siehe Abbildung 7 für eine Illustration in 2 Dimensionen), seine Anwendung auf komplexe, nichtlineare Probleme mit vielen abhängigen Merkmalen einschränken.
Wenn die maximale Baumtiefe zu hoch oder die Mindestanzahl von Datenpunkten pro Blatt zu niedrig angesetzt ist, kann der Entscheidungsbaum überangepasst werden und einzelne Punkte herausfiltern. Dadurch wird der angepasste Entscheidungsbaum weniger verallgemeinerbar und die physikalische Interpretierbarkeit wird untergraben. Dies kann überprüft werden, indem der Datensatz in einen Trainingsdatensatz und einen Testdatensatz aufgeteilt wird. Der Entscheidungsbaum wird mit dem Trainingsdatensatz trainiert, ohne je den Testdatensatz zu sehen. Falls der trainierte Entscheidungsbaum am Testdatensatz bedeutende weniger zuverlässige Vorhersagen liefert als am Trainingsdatensatz ist es wahrscheinlich, dass er überangepasst ist. Dieser Artikel gibt eine Übersicht über Methoden, um Überanpassung zu vermeiden oder abzumindern.
Entscheidungsbäume sind auf einen ausgewogenen Datensatz angewiesen (d.h. mit einer ähnlichen Anzahl Datenpunkte pro Klasse), da sie sonst tendenziell die stärker vertretene Klasse bevorzugen. Dieses Problem kann durch die Einführung von Gewichtungsfaktoren entschärft werden, die allerdings ihr eigenes Problem mit sich bringen, da sie Ausreissern eine übermässige Bedeutung zuschreiben. Falls der Gewichtungsfaktor der weniger vertretenden Klasse fünfmal grösser ist als der der stärker vertretenen Klasse, kann der Entscheidungsbaum ein Blatt mit einem Ausreisser der weniger vertretenen Klasse und vier gültigen Datenpunkten der stärker vertreten Klasse erstellen und dort die weniger vertretene Klasse vorhersagen. Dies ist nur durch eine genaue Plausibilitätskontrolle aller Aufteilungen im Baum bemerkbar. Es ist daher vorzuziehen, ausgewogene Datensätze zu erstellen oder, wenn möglich, vor dem Training des Entscheidungsbaums Ausreisser zu entfernen.
Wie bei allen ML-Modellen hängt das Ergebnis von Entscheidungsbäumen stark von den Daten ab. Man sollte sich bewusst sein, dass kleine Änderungen in den Daten oder auch der Hyperparameter zu einem anderen Entscheidungsbaum führen können. Da Entscheidungsbäume schnell trainiert werden können, empfiehlt es sich, die Hyperparameter zu variieren und zu prüfen, ob die Bäume und ihre Interpretation ähnlich bleiben.
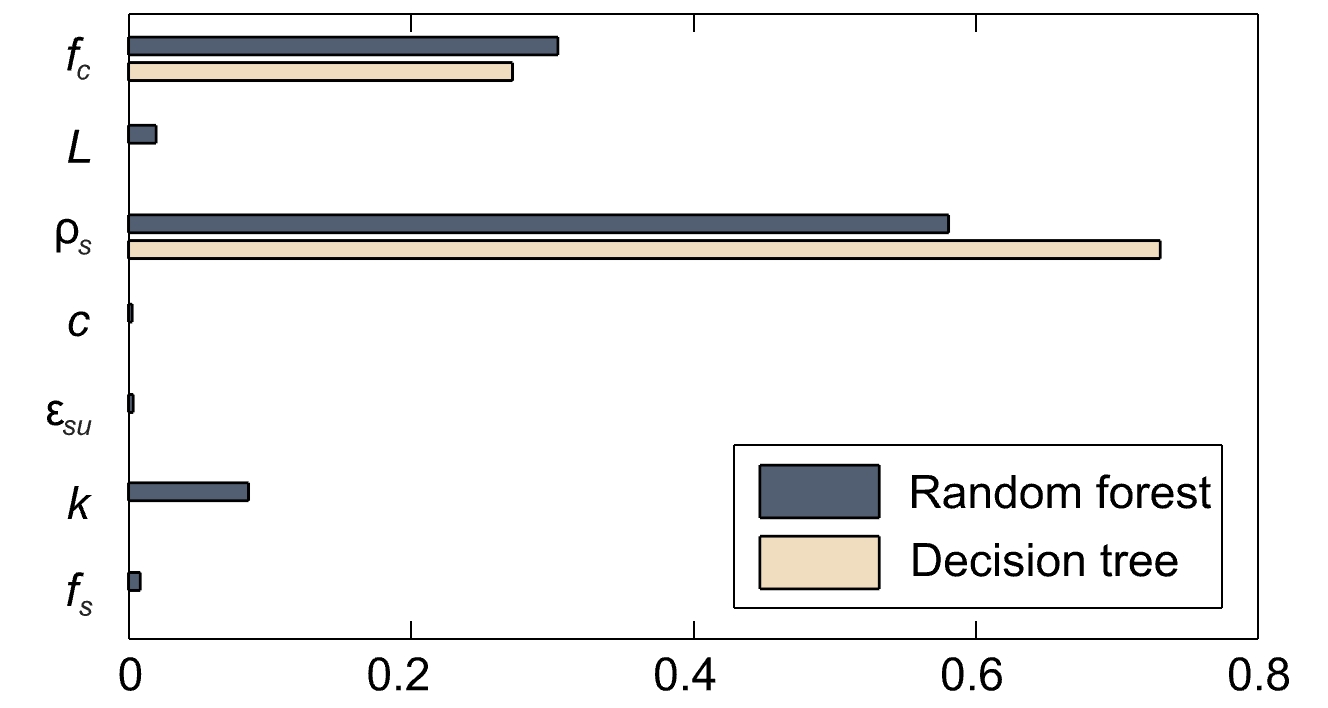
Falls der Entscheidungsbaum nicht genau genug ist, kann man stattdessen ein Random-Forest-Algorithmus nutzen, der während des Trainings mehrere Entscheidungsbäume erzeugt und die Mehrheitsentscheidung dieser Bäume für einen bestimmten Datensatz und bestimmte Hyperparameter liefert. Der Algorithmus kann komplexe Datensätze besser darstellen und ist robuster gegen Überanpassung (siehe diesen Artikel für einen Vergleich). Dies geht jedoch auf Kosten der Erklärbarkeit, da die große Anzahl der generierten Entscheidungsbäume es unpraktisch macht, sie alle manuell zu interpretieren. Bei Random Forests ist es daher üblicher, die relative «Feature Importance» zur Interpretation heranzuziehen, siehe Abbildung 8.
Persönliche Einschätzung
Trotz der Einschränkungen halte ich die Verwendung eines Entscheidungsbaums auf Daten, die von einem bestehenden Modell generiert wurden, für einen interessanten Ansatz, da man mit wenig Aufwand ein besseres Verständnis des Modells und der Daten erlangen kann. Der Prozess hat mir geholfen, mich nicht von der hohen Dimensionalität (viele Merkmale) des mechanischen Modells überwältigen zu lassen, da der Entscheidungsbaum einige Hinweise darauf gab, auf welche Merkmale ich mich konzentrieren sollte. Es hatte auch den Vorteil, dass es meine Kreativität anregte und mich dazu brachte, anders über das Problem nachzudenken, wenn die Ergebnisse nicht mit meinen Erwartungen übereinstimmten. Dies führte dazu, dass ich mein vorläufiges theoretisches Wissen über das Problem vertiefte und schließlich zu einem tieferen Verständnis des mechanischen Modells gelangte.
Ressourcen
Dieses Github-Repository enthält eine kurze Anleitung für den Einstieg ins maschinelle Lernen mit Entscheidungsbäumen (mithilfe der sklearn Toolbox und Visual Studio Code) und das Jupyter Notebook mit dem Code für den Entscheidungsbaum aus Abbildung 1 (Primzahlen).
Nathalie Reckinger