Link to English version: Shear behaviour of lightly reinforced concrete membrane elements
Bei der Beurteilung der Tragsicherheit von bestehenden Tragwerken zeigt sich immer wieder, dass die momentan zur Verfügung stehenden Berechnungsmethoden unzureichend sind, insbesondere betreffend Schubtragfähigkeit. Das liegt daran, dass zur Analyse bestehender Tragwerke in der Regel die gleichen Modelle angewendet werden, die auch für die Bemessung neuer Tragwerke gelten, dass die Querkraftbewehrungsgehalte in alten Bauwerken aber auf Grund der früher geltenden Normbestimmungen oft sehr niedrig sind. In meiner Dissertation, die ich kürzlich erfolgreich verteidigt habe, versuchte ich das Verständnis des Lastverformungsverhaltens von Stahlbeton-Scheibenelementen mit sehr geringen Bewehrungsgehalten im ebenen Spannungszustand zu verbessern.
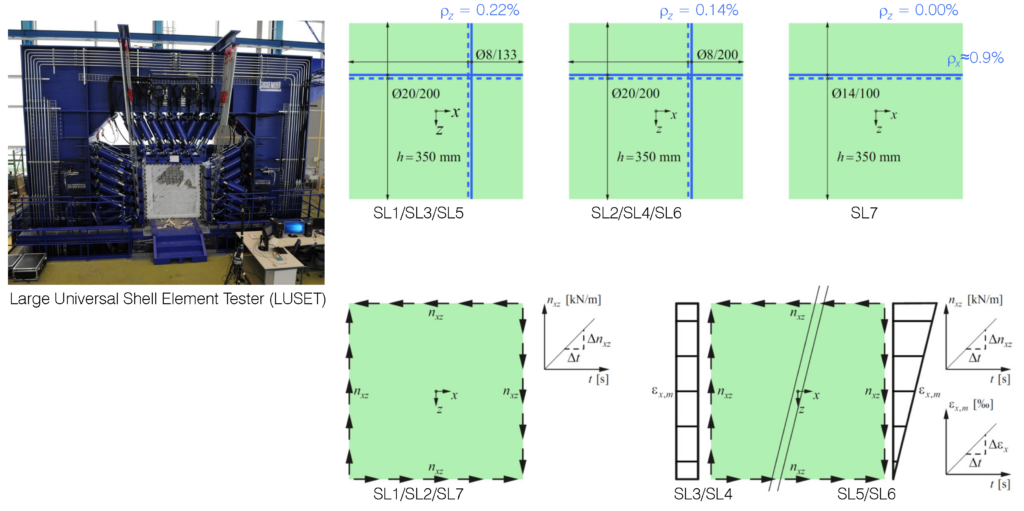
Dazu wurde eine Serie von Schubversuchen an sechs grossformatigen Scheibenelementen mit sehr geringen vertikalen Bewehrungsgehalten von ρz=0.14…0.22%, sowie an einem uniaxial bewehrten Scheibenelement durchgeführt. Drei Elemente wurden unter einer reinen Schubbeanspruchung in der Ebene und vier Elemente unter einer Schubbeanspruchung in der Ebene mit aufgebrachter Längsdehnung mit und ohne Gradient über die Höhe der Versuchskörper getestet. Die Versuche wurden in der neu entwickelten Versuchsanlage Large Universal Shell Element Tester (LUSET) durchgeführt. Dabei kamen moderne Messtechniken zum Einsatz, wobei insbesondere die digitale Bildkorrelation zur Erfassung der Verformungen und Rissbilder auf der Betonoberfläche sowie die faseroptischen Dehnungsmessungen entlang der einbetonierten Bewehrungsstäbe wertvolle und umfassende Daten zur Charakterisierung des Verformungsverhaltens lieferte.
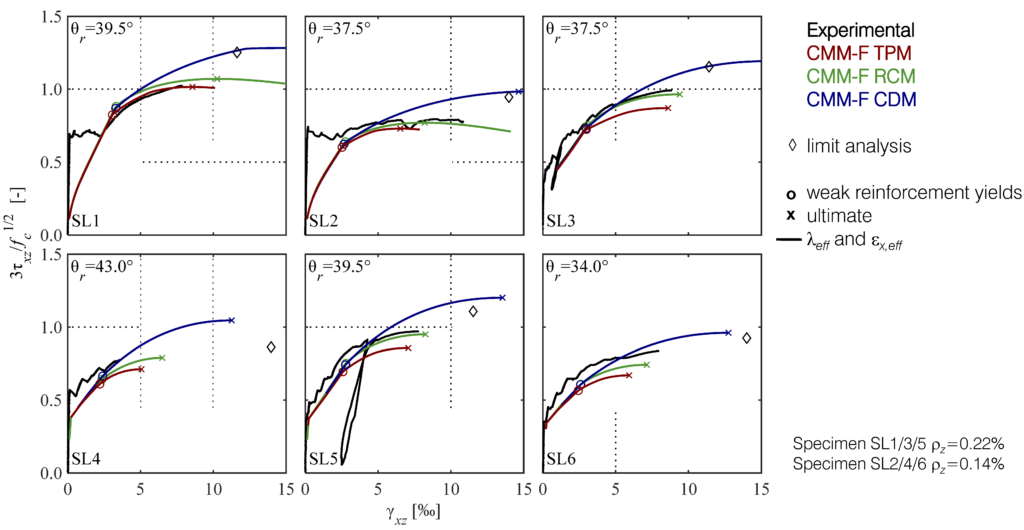
Die Versuchsergebnisse wurden hinsichtlich des Lastverformungsverhaltens der Scheibenelemente, aber auch hinsichtlich ihres Rissverhaltens und der Rissverzahnung (aggregate interlock), d.h. des durch die Unebenheit der Risse entstehenden Verzahnungswiderstandes, mit theoretischen Modellen verglichen. Die Modellvorhersagen bzgl. der Traglast wie auch des Verformungsvermögens des ursprünglich von Prof. Dr. Walter Kaufmann entwickelten gerissenen Scheibenmodells mit fester Rissrichtung (CMM-F) waren hervorragend, insbesondere unter Verwendung des rough crack model (RCM) als Rissverzahnungsmodell. Das RCM ist ein rein empirisches Rissverzahnungsmodell, das mit einer Vielzahl von Versuchen kalibriert wurde. Das CMM-F unter Verwendung des two-phase model (TPM) von Walraven, das ebenfalls empirisch kalibriert wurde, aber auf einem mechanischen Modell basiert und deshalb wohl das am weitesten verbreitete Rissverzahnungsmodell ist, führte zu konservativen Vorhersagen. Dies ist im Hinblick auf die Anwendung von Querkraftmodellen auf Basis des TPM in der Bemessungspraxis positiv zu bewerten (z.B. die Querkraftbestimmungen für Bauteile ohne Schubbewehrung in der SIA 262). Ein weiteres wichtiges Ergebnis der Versuchsserie hinsichtlich der Bemessungspraxis war die Bestätigung der bewährten Empfehlung, bei normalfesten Betonen einen Mindestbewehrungsgehalt von ρz =0,2% vorzusehen. Zu dieser Erkenntnis hat insbesondere geführt, dass die Versuchskörper mit ρz=0.14% eine Bruchlast aufwiesen, die nicht oder nur unwesentlich höher war als die Risslast, während die Last bei den Versuchskörpern mit ρz=0.22% nach dem Reissen noch gesteigert werden konnte. Es wird deshalb davon abgeraten, diesen Wert zu senken, wie dies z.B. gemäss fib MC 2010 oder in der SIA 262 zugelassen ist.
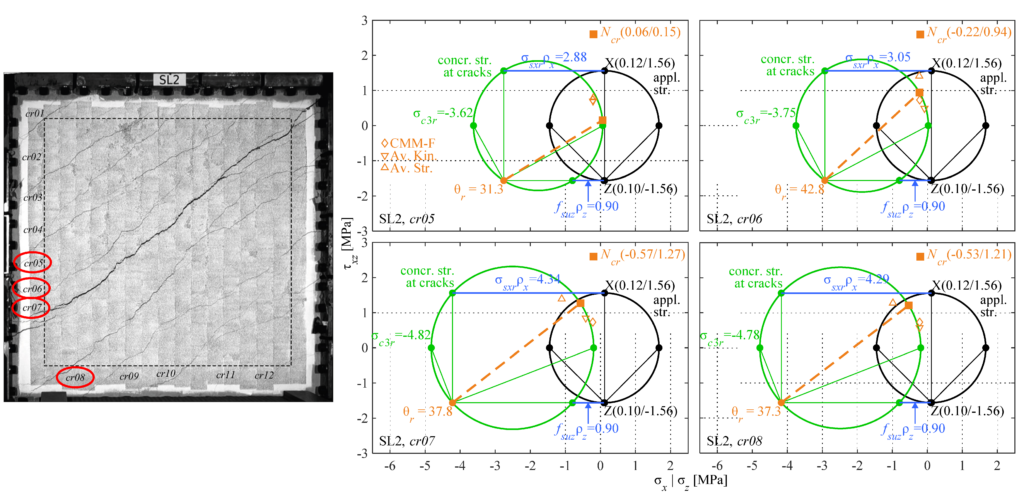
In den Versuchen konnte auch gezeigt werden, dass die verfügbaren Rissverzahnungsmodelle aus der Literatur nur mässig gut funktionieren, wenn es darum geht, die Rissverzahnungsspannungen aus der gemessenen Risskinematik zu bestimmen. Dies war ein Ziel meiner Forschung, um diese Spannungen in Zukunft vielleicht vorhersagen zu können. Die Ergebnisse dieser Berechnungen variierten aber sehr stark. Somit sind die Rissverzahnungsmodelle nicht geeignet, den Spannungszustand eines beliebig geformten Risses in einem Bauteil vorherzusagen. Zudem sind Rissabstände, -neigungen und -formen aufgrund vieler lokaler Einflüsse wie Eigenspannungszuständen, der Variation der Zugfestigkeit innerhalb des Versuchskörpers, unterhalb der Betondeckung verlaufenden Bewehrungsstäben und der Verteilung der Zuschlagstoffe im Beton kaum vorhersagbar.
Alexander Beck