Langzeiteinflüsse bei der Bemessung von monolithisch verbundenen Pfeilern für vorgespannte Träger oder Platten – Concrete E-Learning Platform

Link to the English version: Long-term effects for designing piers monolithically connected to a prestressed girder or slab

In diesem Blogbeitrag geht es um ein technisch anspruchsvolles Thema: die Berücksichtigung von Langzeiteinflüssen (Schwinden und Kriechen) bei der Bemessung von Pfeilern, die monolithisch mit einem vorgespannten Träger oder einer Platte verbunden sind. Dieses strukturelle System findet man in monolithischen Bauwerken oder in Spannbetonbrücken. Wenn Sie sich für Tragwerksplanung begeistern und vielleicht sogar schon in Ihrer beruflichen Praxis damit zu tun hatten wird dieses Thema für Sie von grossem Interesse sein.

Der Entwurf von monolithischen, d.h. fugenlosen Bauwerken setzt sich beim Brückenbau in Europa immer mehr durch. Die Hauptgründe dafür sind zum einen der Wunsch, Probleme der Dauerhaftigkeit zu minimieren und die Instandhaltungskosten zu senken, und zum anderen, dass zunehmend Richtlinien für den Entwurf solcher Bauwerke zur Verfügung stehen. Die Schweiz ist ein Referenzland, das zur Entwicklung dieser Art von Bauwerken beigetragen hat. Traditionell werden Betonbrücken mit monolithisch mit der Fahrbahn verbundenen Pfeilern und halbintegrale oder integrale Brücken (monolithische Verbindung an beiden Widerlagern) [1], wo immer möglich, bevorzugt [2]. In der Schweiz wurden zahlreiche fugenlose Brücken [3][4][5][6][7] gebaut, und technische Richtlinien fördern integrale oder semi-integrale Brücken [1][2] (alte Referenz¹ aus den 70er Jahren). Angesichts der daraus resultierenden Tendenz, immer längere monolithische, fugenlose Brücken zu bauen, sind immer genauere und komplexere Berechnungen erforderlich, um die Pfeiler zuverlässig zu bemessen. Vor etwa zehn Jahren hatte ich die Gelegenheit, an einer Veröffentlichung mitzuwirken, die Ingenieure bei der Bemessung von Pfeilern langer fugenloser Betonbauwerke unterstützt [8]. Dieses Dokument ist allerdings auf Bauwerke beschränkt, bei denen die Platte oder der Träger nicht vorgespannt ist.

Trotz der Verfügbarkeit leistungsfähiger Statiksoftware bleibt die Analyse statisch unbestimmter Strukturen, die Langzeiteinflüssen ausgesetzt sind, eine Herausforderung. Ein anschauliches Beispiel dafür, das wir in diesem Blog erörtern werden, ist die Abschätzung der Biegemomente aufgrund von Langzeiteinflüssen in einem Betonpfeiler, der monolithisch mit einem vorgespannten Träger verbunden ist. Bei dieser Art von Bauwerk ist ein grosser Teil der Kräfte, die im Pfeiler wirken, auf die Verformungen zurückzuführen, die dem Pfeilerkopf durch das Deck aufgezwungen werden und die in den Grenzzuständen der Gebrauchstauglichkeit (GZG) und der Tragsicherheit (GZT Typ 2 und GZT Typ 4²) relevant sind. Die Ermittlung der durch Langzeiteinflüsse verursachten Schnittgrössen im Pfeiler mit akzeptabler Genauigkeit ist jedoch kompliziert, da die Spannungen über der Zeit nichtlinear variieren (der Elastizitätsmodul variiert mit dem Alter des Betons), der Träger und der Pfeiler nicht gleichmässig kriechen (unterschiedliche Kriechkoeffizienten, d. h. unterschiedliche Betone und unterschiedliches Alter) und die gerissene Biegesteifigkeit über die Pfeilerhöhe variiert und von der Belastungsgeschichte abhängt (maximale Zugspannung). Um die Schnittgrössen in den Pfeilern einfach abschätzen zu können, berücksichtigen die Ingenieure in der üblichen Ingenieurpraxis daher in der Regel (i) reduzierte Pfeilerbiegesteifigkeiten aufgrund von Rissen (im Allgemeinen konstant oder linear variabel entlang der Pfeiler), die durch Iteration berechnet werden und für GZG-, GZT Typ 2- und GZT Typ 4-Nachweise unterschiedlich sind, (ii) etwa 40…50% des gesamten Schwindens der Fahrbahnplatte zur Zeit t = ∞, um die Langzeiteinflüsse zu berücksichtigen, aber (iii) vernachlässigen Langzeiteinflüsse aufgrund der Vorspannung mit der Begründung, dass das Kriechen des Pfeilers die Zunahme der Pfeilerkopfverschiebung aufgrund des Kriechens des Trägers kompensiert.

Die erste Vereinfachung kann im Allgemeinen akzeptiert werden, wenn sie mit dem nötigen technischen Sachverstand durchgeführt wird, sollte aber durch eine Sensitivitätsstudie ergänzt werden, um die Unsicherheiten der Berechnungen abzudecken. In Bezug auf die zweite und dritte Vereinfachung stellen sich jedoch unweigerlich folgende Fragen: Ist dieser Ansatz angemessen und unter welchen Bedingungen ist er gültig? Was ist der Hintergrund? Ist dieser Ansatz konservativ? Ist es notwendig, eine Sensitivitätsanalyse durchzuführen, um Unsicherheiten abzudecken, wenn diese Massnahme für den Entwurf entscheidend ist?

Nach dieser Einführung ist es nun an der Zeit, diese Fragen zu beantworten. Im Folgenden werden Sie und ich das formulierte Problem analytisch lösen, die Ergebnisse interpretieren und einige Schlussfolgerungen ziehen. Das zu untersuchende Bauwerk ist in Abbildung 1 vereinfacht dargestellt. Das horizontale Element stellt einen Spannbetonträger dar, das vertikale Element einen Pfeiler mit der Höhe h, der monolithisch mit dem Träger in einem Abstand L_T (Ausdehnungslänge) vom Fixpunkt verbunden ist. Die mechanischen Eigenschaften sind für beide Elemente konstant und sind in Abbildung 1(a) dargestellt. Abbildung 1(b) und Abbildung 1(c) zeigen die horizontalen Verschiebungen des Pfeilerkopfes über die Zeit, u_h,_εcs(t) und u_h,P,el(t), verursacht durch das Schwinden e_cs(t) bzw. die Vorspannung P(t) des Trägers. Beachten Sie, dass die Einspannung des Pfeilers in die horizontalen Verschiebungen des Trägers vernachlässigt wird, da die axiale Steifigkeit des Trägers im Allgemeinen um Grössenordnungen höher ist als die horizontale (Biege-)Steifigkeit des Pfeilers. Darüber hinaus wurden für die in Abbildung 1(c) dargestellten Gleichungen folgende Annahmen getroffen: Normalkraft konstant entlang des Trägers (keine Vorspannungkraftverluste durch Reibung) und E_PI_P<<E_GI_G, d.h. Pfeiler “perfekt” doppelt eingespannt. Es ist zu beachten, dass die letztgenannte Überlegung für einige Fälle nicht geeignet ist, z. B. für Bauwerke, bei denen die Biegesteifigkeit der Stütze im Vergleich zu der des Trägers nicht vernachlässigbar ist, oder für flexible Fundamente (Tiefgründungen). Die im Folgenden berechneten Langzeiteinflüsse werden jedoch unabhängig von den Steifigkeiten der Pfeiler und der Fahrbahnplatte formuliert, die direkt als aufgezwungene Verformungen in die Finite-Elemente-Analyse (FEA) einbezogen werden können. Darüber hinaus wird der Einfluss des Kriechens des Pfeilers auf die entsprechenden (ungerissenen und gerissenen) Biegesteifigkeiten in den folgenden Berechnungen nicht berücksichtigt, so dass die äquivalente reduzierte Biegesteifigkeit des Pfeilers unter Berücksichtigung von Kriechen und Rissbildung im statischen System verwendet werden sollte.

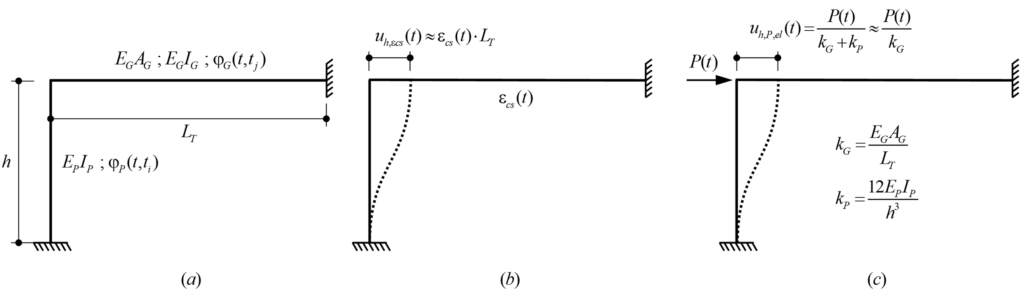
Abbildung 1. Pfeiler, der monolithisch mit einem vorgespannten Träger verbunden ist. (a) Mechanische Eigenschaften; (b) horizontale Verschiebungen über die Zeit aufgrund von Schwinden; (c) horizontale Verschiebungen über die Zeit aufgrund von Vorspannung

*E_G:* Elastizitätsmodul des Trägers
*E_P:* Elastizitätsmodul des Pfeilers
I_G: Flächenträgheitsmoment des Trägers
I_P: Flächenträgheitsmoment des Pfeilers
φ_G(*t,t_j*): Kriechkoeffizient des Trägers
φ_P(*t,t_i*): Kriechkoeffizient des Pfeilers

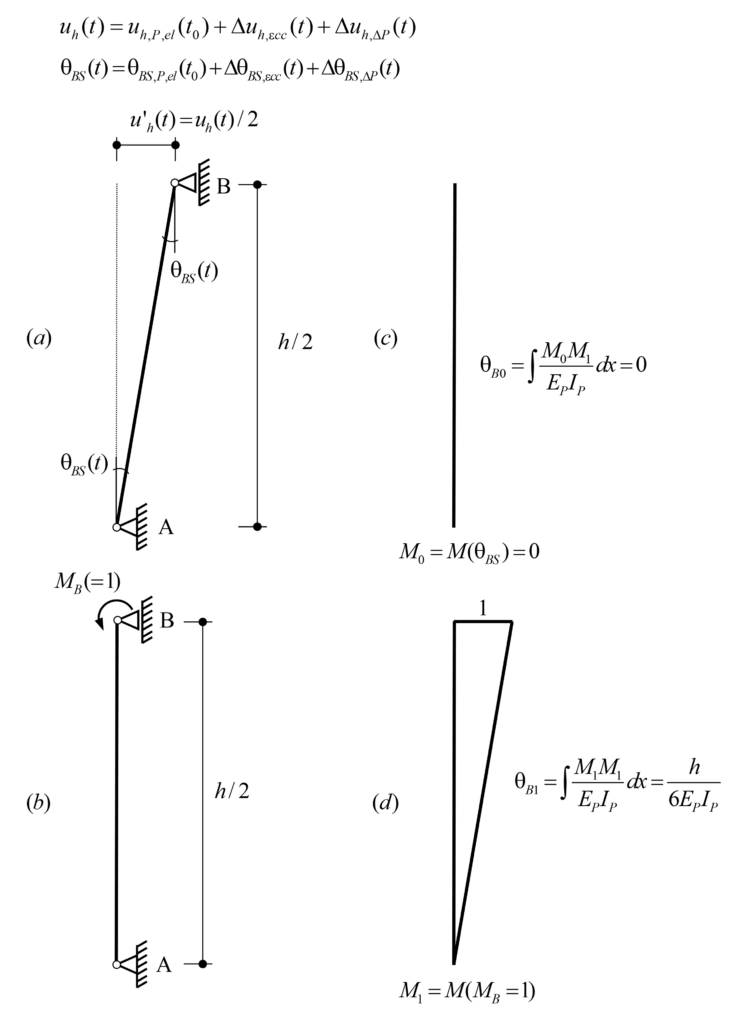
Um das System analytisch zu lösen, wird die Rahmenstruktur aus Abbildung 1 gemäss Abbildung 2 vereinfacht. Um die Schnittgrössen im Pfeiler infolge der aufgezwungenen horizontalen Verschiebung u_h, zu erhalten, kann der isolierte doppelt-eingespannte Pfeiler der Höhe h (Abbildung 2 (a)) durch den isolierten gelenkig eingespannten Pfeiler der Höhe h/2 (Abbildung 2 (b)) ersetzt werden. Abbildung 2(c) zeigt somit das äquivalente vereinfachte System zur Ermittlung der Schnittgrössen im Pfeiler infolge einer horizontalen Verschiebung u’_h am Pfeilerkopf, die gleich der Hälfte der horizontalen Verschiebung u_h im ursprünglichen System (Abbildung 1) ist, d. h. u’_h (t)= u_h(t)/2. Um die korrekte Verschiebung des Pfeilerkopfes infolge der Vorspannung zu erhalten, ist die äquivalente Vorspannkraft P’ (t) im vereinfachten System (Abbildung 2(c)) gleich der Hälfte der Vorspannkraft P(t)/2 im ursprünglichen System (Abbildung 1), wenn die Biegesteifigkeit des Pfeilers gegenüber der axialen Steifigkeit des Trägers vernachlässigt wird, andernfalls wird sie wie folgt bestimmt:

$\begin{align*}& P'(t)=\frac{P(t)}{2}\left( \frac{{{k}_{G}}+k{{'}_{P}}}{{{k}_{G}}+{{k}_{P}}} \right) \\& k{{'}_{P}}=\frac{3{{E}_{P}}{{I}_{P}}}{{{\left( {h}/{2}\; \right)}^{3}}}=\frac{24{{E}_{P}}{{I}_{P}}}{{{h}^{3}}} \\& {{k}_{P}}\text{ and }k{{'}_{P}}\text{ }\ll \text{ }{{k}_{G}}\to \text{ }P'(t)\approx \frac{P(t)}{2} \\\end{align*}$

Abbildung 2. (a) Isolierter doppelt-eingespannter Pfeiler; (b) isolierter gelenkig-eingespannter Pfeiler; (c) äquivalentes vereinfachtes System von Abbildung 1

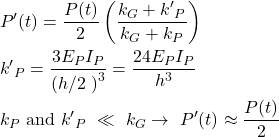
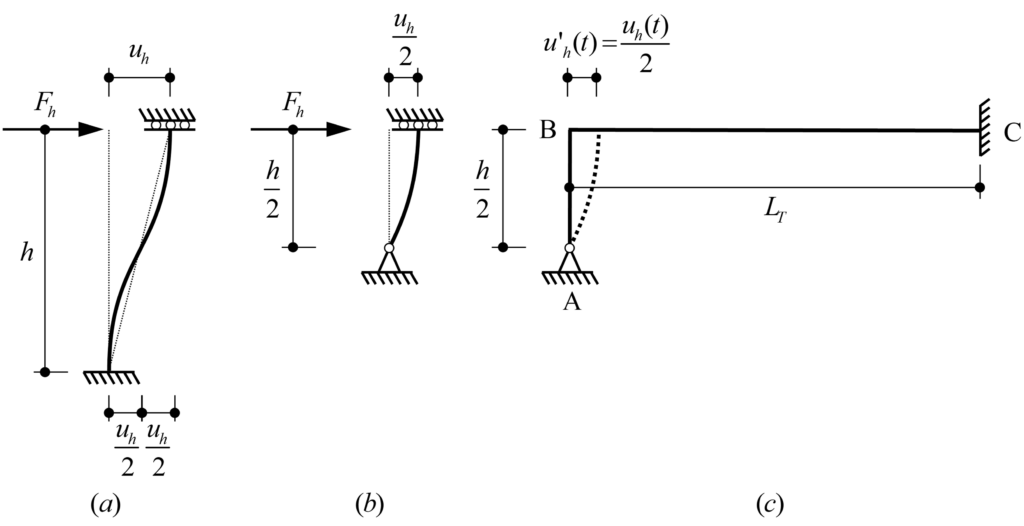
Im Folgenden isolieren wir den Pfeiler des in Abbildung 2(c) dargestellten vereinfachten Systems und lösen ein System, das aus einem Pfeiler mit einem einzigen Grad statischer Unbestimmtheit besteht, indem wir die zeitabhängige Kraftmethode anwenden und die Kompatibilitätsgleichungen über die Zeit formulieren, wobei:

BS (Basissystem): Feste Rotation in B (Pfeilerkopf) freigegeben

ÜG (Überzählige Grösse): Biegemoment in B (Pfeilerkopf)

Zusätzlich werden die zeitabhängigen Biegemomente am Pfeilerkopf infolge Schwinden und Vorspannung separat berechnet.

Zeitabhängiges Verhalten von Betonpfeilern

1. Schwinden (zeitabhängige Pfeilerkopfverschiebung³)

Abbildung 3 zeigt den isolierten Pfeiler mit dem Basissystem (BS) und der überzähligen Grösse (ÜG), die zur Bestimmung des Biegemoments M_B(t) mit Hilfe der Kraftmethode verwendet wird. Da sich das Biegemoment M_B(t) über die Zeit verändert, wird die Kompatibilität am Auflager B sowohl zum Anfangszeitpunkt als auch zeitabhängig ausgedrückt.

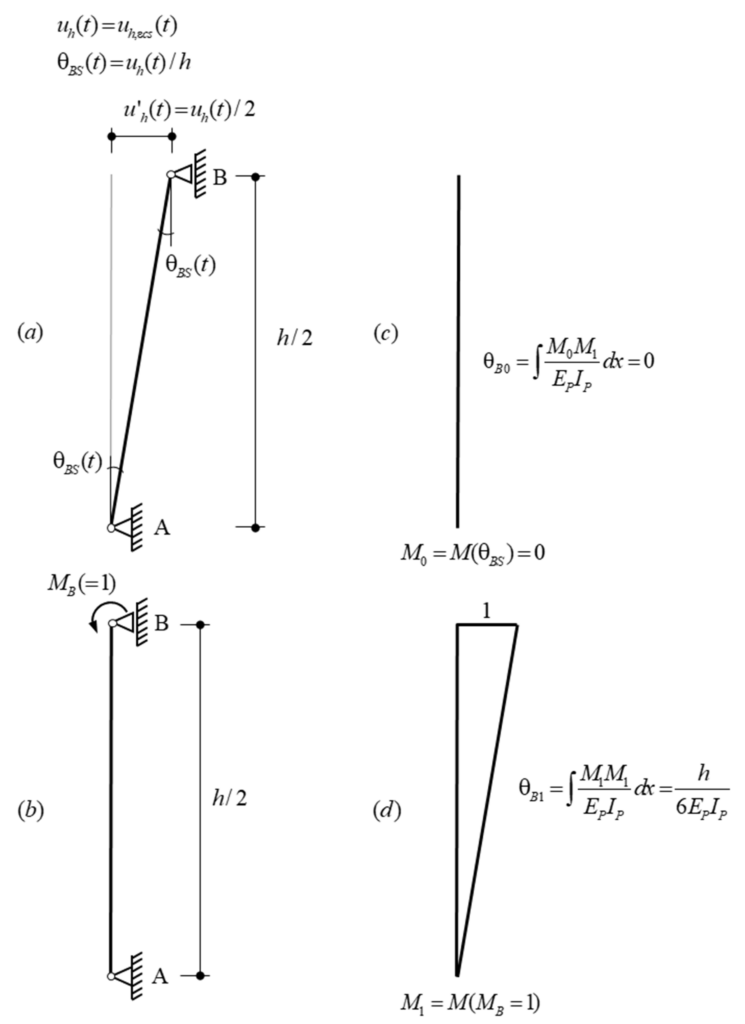
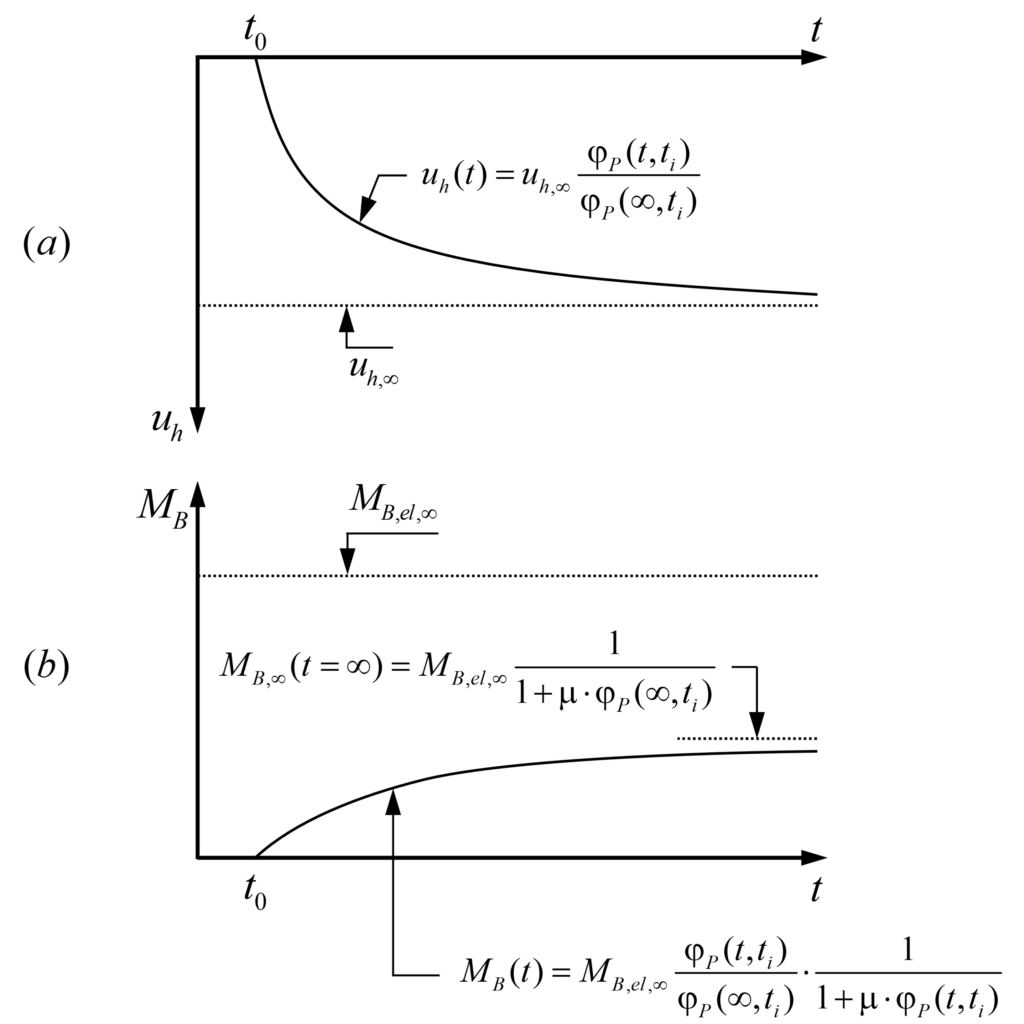
Abbildung 3. Zeitabhängige Pfeilerkopfverschiebung (Schwindung des Trägers). (a) Basissystem (BS) mit erzwungener Pfeilerkopfverschiebung; (b) BS mit überzähliger Grösse (ÜG); (c) und (d) entsprechende Biegemomentdiagramme

Das Schwinden ε_cs(t) des Trägers verursacht eine Verformung über die Zeit, die horizontale Verschiebungen u_h(t) und Biegemomente M_B(t) am Pfeilerkopf erzeugt. Zum Anfangszeitpunkt sind sowohl die horizontale Verschiebung u_h(t₀) als auch das Biegemoment M_B(t₀) Null (kein Schwinden). Zu jedem beliebigen Zeitpunkt t > t₀, ist der Träger um ε_cs(t) geschwunden, was zu einer horizontalen Verschiebung u_h(t) und einem Biegemoment M_B(t) führt, siehe Abbildung 4(a) bzw. Abbildung 4(b). Unter der Annahme, dass das Schwinden des Trägers und damit die aufgezwungenen Verformungen über die Zeit u_h(t) proportional zur Kriechfunktion des Pfeilers sind, kann u_h(t) wie folgt ausgedrückt werden:

${{u}_{h}}(t)={{u}_{h,\infty }}\frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})}\text{ (Gl}\text{. 1)}$

Daher erreicht die horizontale Verschiebung am Pfeilerkopf zur Zeit t = ∞ die maximale horizontale Verschiebung u_h,∞ = ε_cs_,∞·L_T (Abbildung 4(a)). Wie wir jedoch weiter unten sehen werden, wird das Biegemoment M_B,∞ (t=∞) geringer sein als das elastische Biegemoment M_B,el,∞ das durch die maximale horizontale Verschiebung u_h,∞ verursacht wird (Abbildung 4(b)).

Das Biegemoment M_B(t) am Pfeilerkopf kann wie folgt formuliert werden:

${{M}_{B}}(t)=\cancel{{{M}_{B}}({{t}_{0}})}+\Delta {{M}_{B}}(t)=\Delta {{M}_{B}}(t)\text{ (Gl}\text{. 2)}$

Dabei ist ΔM_B(t) die Zunahme des Biegemoments über die Zeit infolge des Schwindens.

Abbildung 4. Horizontale Verschiebungen *u_h*(t) (a) und Biegemomente *M_B*(t) (b) am Pfeilerkopf über die Zeit infolge des Schwindens

Rotationskompatibilitätsbedingung zum Anfangszeitpunkt t=t₀:

Die Rotationskompatibilität zum Anfangszeitpunkt (man beachte, dass alle Operationen im Basissystem (BS) angewendet werden) ergibt den Ausdruck:

${{\theta }_{B}}({{t}_{0}})=\cancel{{{\theta }_{B0}}}+{{M}_{B}}({{t}_{0}})\cdot {{\theta }_{B1}}={{\theta }_{BS}}({{t}_{0}})=0\to {{M}_{B}}({{t}_{0}})=\frac{\cancel{{{\theta }_{BS}}({{t}_{0}})}}{{{\theta }_{B1}}}=0\text{ (Gl}\text{. 3)}$

Wie bereits erwähnt, ist das Biegemoment am Pfeilerkopf zum Anfangszeitpunkt gleich Null M_B(t₀) = 0, da das Schwinden noch nicht eingesetzt hat.

Zeitabhängige Rotationskompatibilitätsbedingung (Methode von Trost):

Die Entwicklung der zeitabhängigen Rotationskompatibilität erfolgt nach der Methode von Trost. Wenn Sie mit dieser Methode nicht vertraut sind, empfehle ich Ihnen unsere Vorlesung zu Langzeiteinflüssen in Advanced Structural Concrete.

$\begin{align*}& {{\theta }_{B}}(t)=\cancel{{{\theta }_{B0}}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+\cancel{{{M}_{B}}({{t}_{0}})}\cdot {{\theta }_{B1}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+\Delta {{M}_{B}}(t)\cdot {{\theta }_{B1}}\left[ 1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]={{\theta }_{BS}}(t)\text{ (Gl. 4)} \\& {{\theta }_{BS}}(t)={{\theta }_{BS,\infty }}\frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})} \\& \Delta {{M}_{B}}(t)={{M}_{B}}(t)=\frac{{{\theta }_{BS,\infty }}}{{{\theta }_{B1}}}\cdot \frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})}\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})} \\& {{M}_{B,el,\infty }}=\frac{{{\theta }_{BS,\infty }}}{{{\theta }_{B1}}}=\frac{6{{E}_{P}}{{I}_{P}}}{{{h}^{2}}}{{\varepsilon }_{cs,\infty }}{{L}_{T}}\text{ (Gl}\text{. 5)} \\& {{M}_{B}}(t)={{M}_{B,el,\infty }}\cdot \frac{{{\varphi }_{P}}(t,{{t}_{i}})}{{{\varphi }_{P}}(\infty ,{{t}_{i}})}\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 6)} \\& {{M}_{B,\infty }}(t=\infty )={{M}_{B,el,\infty }}\frac{1}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})}\text{ (Gl}\text{. 7)} \\\end{align*}$

Beachten Sie, dass die Kompatibilitätsgleichung (Gl. 4) ausdrückt, dass die durch das Biegemoment M_B(t) verursachte Rotation θ_B(t) (überzählige Grösse ÜG) die Rotation aufgrund der Pfeilerkopfverschiebung θ_BS(t) kompensieren muss; beide Rotationen werden im Basissystem bestimmt. Mit anderen Worten, die Gesamtrotation des Pfeilerkopfes B muss gleich Null sein (siehe Abbildung 3). Der von Trost eingeführte Alterungskoeffizient μ⁴ trägt der Tatsache Rechnung, dass der Beton bei später einwirkenden Lasten weniger kriecht. Aus dieser Bedingung lässt sich das Biegemoment M_B(t) zu jedem Zeitpunkt t bestimmen (Gl. 6) und in Form des elastischen Biegemoments M_B,el,∞ (Gl. 5) ausdrücken.

2. Vorspannung

Im Gegensatz zum Schwinden, bei dem die horizontale Verschiebung am Pfeilerkopf von Null zum Anfangszeitpunkt zunimmt, ist die Vorspannung eine sofortige Einwirkung zum Anfangszeitpunkt (t=t₀), die eine anfängliche horizontale Verschiebung u_h(t₀) = u_h,P,el(t₀) und ein entsprechendes anfängliches elastisches Biegemoment M_B(t₀) = M_B,el(t₀) am Pfeilerkopf verursacht. Danach ändern sich sowohl die horizontale Verschiebung u_h(t) als auch das Biegemoment M_B(t) über die Zeit.

Ähnlich wie bei der Berechnung der Biegemomente infolge Schwinden wird der Pfeiler isoliert und das Basissystem (BS) mit dem Biegemoment am Pfeilerkopf B M_B(t) als überzählige Grösse verwendet, siehe Abbildung 5.

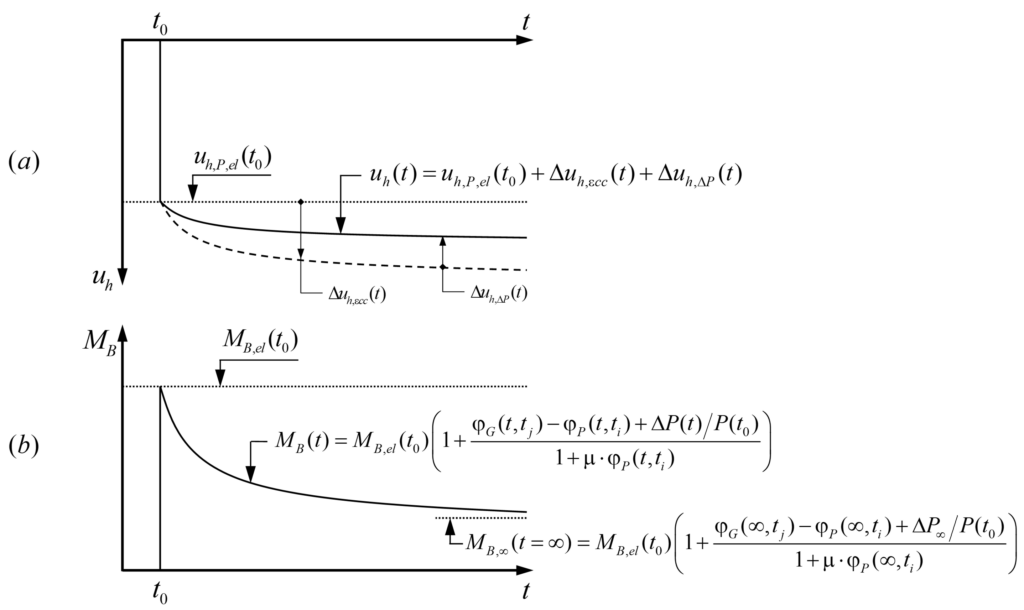
Abbildung 5. Zeitabhängige Pfeilerkopfverschiebung (Vorspannung). (a) Basissystem (BS) mit erzwungener Pfeilerkopfverschiebung; (b) BS mit überzähliger Grösse (ÜG); (c) und (d) entsprechende Biegemomentdiagramme

Die gesamte horizontale Verschiebung am Pfeilerkopf u_h(t) infolge der Vorspannung beträgt:

${{u}_{h}}(t)={{u}_{h,P,el}}({{t}_{0}})+\Delta {{u}_{h,\varepsilon cc}}(t)+\Delta {{u}_{h,\Delta P}}(t)\text{ (Gl}\text{. 8)}$

wobei,

u_h,P,el(t₀) die anfängliche horizontale Verschiebung am Pfeilerkopf infolge der elastischen Verformung des Trägers durch die anfängliche Vorspannkraft P(t₀) ist, d.h.,

${{u}_{h,P,el}}({{t}_{0}})=\frac{P({{t}_{0}})}{{{k}_{G}}}\text{ (zeitunabh }\!\!\ddot{\mathrm{a}}\!\!\text{ ngige Pfeilerkopfverschiebung) (Gl}\text{. 9)}$

Δu_h,ecc(t) ist der horizontale Verschiebungszuwachs am Pfeilerkopf über die Zeit aufgrund von Langzeiteffekten, die durch das Kriechen des Trägers φ_G(t,t_j) verursacht werden.

$\Delta {{u}_{h,\varepsilon cc}}(t)={{\varphi }_{G}}(t,{{t}_{j}})\cdot {{u}_{h,P,el}}({{t}_{0}}\text{) (zeitabh }\!\!\ddot{\mathrm{a}}\!\!\text{ ngige Pfeilerkopfverschiebung) (Gl}\text{. 10)}$

Δu_h,_D_P(t) ist der horizontale Verschiebungszuwachs am Pfeilerkopf über die Zeit infolge der Änderung der Vorspannkraft ΔP(t) (Vorspannkraftverluste) über die Zeit aufgrund von Schwinden, Kriechen und Relaxation. Sie wird als proportional zur anfänglichen horizontalen Verschiebung u_h,P,el(t₀) betrachtet und hat einen negativen Wert, da ΔP(t) <0:

$\Delta {{u}_{h,\Delta P}}(t)=\frac{\Delta P(t)}{P({{t}_{0}})}\cdot {{u}_{h,P,el}}({{t}_{0}})\text{ (zeitabh }\!\!\ddot{\mathrm{a}}\!\!\text{ ngige Pfeilerkopfverschiebung) (Gl}\text{. 11)}$

Wenn die Vorspannkraft zum Anfangszeitpunkt (t=t₀) aufgebracht wird, weist der Pfeilerkopf eine anfängliche horizontale elastische Verschiebung u_h,P,el(t₀) auf. Anschliessend nimmt die horizontale Verschiebung aufgrund des Kriechens des Trägers Δu_h,εcc(t) mit der Zeit zu, was teilweise durch die Abnahme der Vorspannkraft aufgrund der Vorspannkraftverluste Δu_h,_Δ_P(t) kompensiert wird, siehe Abbildung 6(a). Andererseits wird das Biegemoment M_B,el(t₀) im Pfeilerkopf, das durch die aufgezwungene horizontale Verschiebung u_h,P,el(t₀), die elastische Verformung des Trägers infolge der Vorspannung, verursacht wird, im Laufe der Zeit aufgrund des Kriechens und der Vorspannkraftverluste ΔP(t) des Pfeilers verringert (Abbildung 6(b)). Das Biegemoment M_B(t) kann wie folgt ausgedrückt werden:

${{M}_{B}}(t)={{M}_{B,el}}({{t}_{0}})+\Delta {{M}_{B}}(t)\text{ (Gl}\text{. 12)}$

Dabei ist ΔM_B(t) die Zunahme des Biegemoments über die Zeit aufgrund des Kriechens des Pfeilers und des Trägers sowie der Vorspannkraftverluste.

Abbildung 6. Horizontale Verschiebungen *u_h*(t) (a) und Biegemomente M_B(t) (b) am Pfeilerkopf über die Zeit aufgrund von Vorspannung

Für die Berechnung der Biegemomente M_B(t) am Pfeilerkopf über die Zeit wird, ähnlich wie bei der Berechnung des Schwindens, erstens die Rotationskompatibilität zum Anfangszeitpunkt und zweitens die zeitabhängige Rotationskompatibilität nach der Methode von Trost angewendet.

Rotationskompatibilitätsbedingung zum Anfangszeitpunkt t=t₀:

Die Rotationskompatibilität im Basissystem (BS) zum Anfangszeitpunkt (Abbildung 5) ergibt:

$\begin{align*} & {{\theta }_{B}}({{t}_{0}})=\cancel{{{\theta }_{B0}}}+{{M}_{B}}({{t}_{0}})\cdot {{\theta }_{B1}}={{\theta }_{BS,P,el}}({{t}_{0}})+\cancel{\Delta {{\theta }_{BS,\varepsilon cc}}({{t}_{0}})}+\cancel{\Delta {{\theta }_{BS,\Delta P}}({{t}_{0}})}\text{ (Gl}\text{. 13)} \\ & {{M}_{B}}({{t}_{0}})=\frac{{{\theta }_{BS}}({{t}_{0}})}{{{\theta }_{B1}}}={{M}_{B,el}}({{t}_{0}})\text{ (Gl}\text{. 14)} \\\end{align*}$

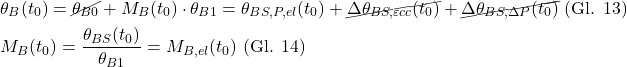
Das anfängliche Biegemoment M_B(t₀) am Pfeilerkopf ist gleich dem anfänglichen elastischen Biegemoment M_B,el(t₀), siehe Gl. 14.

Zeitabhängige Rotationskompatibilitätsbedingung (Methode von Trost):

Im Folgenden werden die Gleichungen mit Hilfe der Methode von Trost entwickelt, um den Biegemomentzuwachs am Pfeilerkopf über die Zeit ΔM_B(t) zu bestimmen.

${{\theta }_{B}}(t)={{\theta }_{B0}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+{{M}_{B}}({{t}_{0}})\cdot {{\theta }_{B1}}\left[ 1+{{\varphi }_{P}}(t,{{t}_{i}}) \right]+\Delta {{M}_{B}}(t)\cdot {{\theta }_{B1}}\left[ 1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]={{\theta }_{BS,P,el}}({{t}_{0}})+\Delta {{\theta }_{BS,\varepsilon cc}}(t)+\Delta {{\theta }_{BS,\Delta P}}(t)\text{ (Gl}\text{. 15)}$

Beachten Sie, dass die Rotation am Auflager B θ_B(t) über die Zeit, analog zur horizontalen Verschiebung, ergibt:

${{\theta }_{B}}(t)={{\theta }_{B,P,el}}({{t}_{0}})+\Delta {{\theta }_{B,\varepsilon cc}}(t)+\Delta {{\theta }_{B,\Delta P}}(t)$

wobei,

$\begin{align*} & {{\theta }_{B,P,el}}({{t}_{0}})={{{u}_{h,P,el}}({{t}_{0}})}/{h}\; \\ & \Delta {{\theta }_{B,\varepsilon cc}}(t)={{{u}_{h,\varepsilon cc}}(t)}/{h}\; \\ & \Delta {{\theta }_{B,\Delta P}}(t)={{{u}_{h,\Delta P}}(t)}/{h}\; \\\end{align*}$

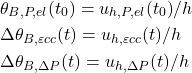
Durch Substitution von Gl. 13 und Gl. 14 in Gl. 15:

$\begin{align*} & {{\theta }_{B}}(t)={{M}_{B,el}}({{t}_{0}})\cdot {{\theta }_{B1}}\cdot {{\varphi }_{P}}(t,{{t}_{i}})+\Delta {{M}_{B}}(t)\cdot {{\theta }_{B1}}\left[ 1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]=\Delta {{\theta }_{BS,\varepsilon cc}}(t)+\Delta {{\theta }_{BS,\Delta P}}(t)\text{ (Gl}\text{. 16)} \\ & \Delta {{M}_{B}}(t)=\left[ \frac{\Delta {{\theta }_{BS,\varepsilon cc}}(t)}{{{\theta }_{B1}}}+\frac{\Delta {{\theta }_{BS,\Delta P}}(t)}{{{\theta }_{B1}}}-{{M}_{B,el}}({{t}_{0}})\cdot {{\varphi }_{P}}(t,{{t}_{i}}) \right]\cdot \frac{1}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 17)} \\\end{align*}$

Andererseits kann angenommen werden, dass das Biegemoment und die Rotation am Pfeilerkopf proportional zur horizontalen Verschiebung über die Zeit sind. Daher kann man aus Gl. 10 und Gl. 11 die Biegemomenterhöhungen ΔM_B,_ε_cc,el(t) und ΔM_B,_Δ_P,el(t) aufgrund von Kriech- bzw. Vorspannkraftverlusten wie folgt formulieren:

$\begin{align*} & \frac{\Delta {{\theta }_{BS,\varepsilon cc}}(t)}{{{\theta }_{B1}}}=\Delta {{M}_{B,\varepsilon cc,el}}(t)={{\varphi }_{G}}(t,{{t}_{j}})\cdot {{M}_{B,el}}({{t}_{0}})\text{ (Gl}\text{. 18)} \\& \frac{\Delta {{\theta }_{BS,\Delta P}}(t)}{{{\theta }_{B1}}}=\Delta {{M}_{B,\Delta P,el}}(t)=\frac{\Delta P(t)}{P({{t}_{0}})}\cdot {{M}_{B,el}}({{t}_{0}})\text{ (Gl}\text{. 19)} \\\end{align*}$

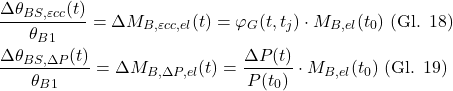
Durch Substitution von Gl. 18 und Gl. 19 in Gl. 17:

$\Delta {{M}_{B}}(t)={{M}_{B,el}}({{t}_{0}})\cdot \frac{{{\varphi }_{G}}(t,{{t}_{j}})-{{\varphi }_{P}}(t,{{t}_{i}})+\frac{\Delta P(t)}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})}\text{ (Gl}\text{. 20)}$

Durch Einsetzen des Biegemomentinkrements ΔM_B(t) aus Gl. 20 in Gl. 12 ergibt sich schliesslich das Gesamtbiegemoment am Pfeilerkopf über die Zeit M_B(t) wie folgt:

$\begin{align*}& {{M}_{B}}(t)={{M}_{B,el}}({{t}_{0}})\cdot \left( 1+\frac{{{\varphi }_{G}}(t,{{t}_{j}})-{{\varphi }_{P}}(t,{{t}_{i}})+\frac{\Delta P(t)}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(t,{{t}_{i}})} \right)\text{ (Gl}\text{. 21)} \\& {{M}_{B,\infty }}(t=\infty )={{M}_{B,el}}({{t}_{0}})\cdot \left( 1+\frac{{{\varphi }_{G}}(\infty ,{{t}_{j}})-{{\varphi }_{P}}(\infty ,{{t}_{i}})+\frac{\Delta {{P}_{\infty }}}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})} \right)\text{ (Gl}\text{. 22)} \\\end{align*}$

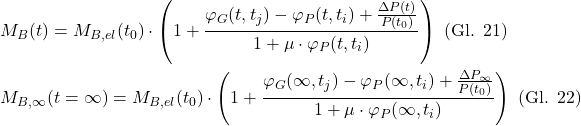
3. Zusammenfassung und Diskussion

Schwinden:

Das Biegemoment M_B,∞ am Pfeilerkopf zur Zeit t = ∞ infolge des Schwindens ist wie folgt:

${{M}_{B,\infty }}={{M}_{B,el,\infty }}\frac{1}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})}$

Dabei ist μ ≈ 0.80 und t_i das Alter des Pfeilerbetons, wenn der Träger zu schwinden beginnt. Abbildung 7 zeigt das Verhältnis zwischen dem Biegemoment M_B,∞ und dem elastischen Biegemoment M_B,el,∞ am Pfeilerkopf zur Zeit t = ∞ als Funktion des Pfeiler-Kriechkoeffizienten φ_P(∞,t_i).

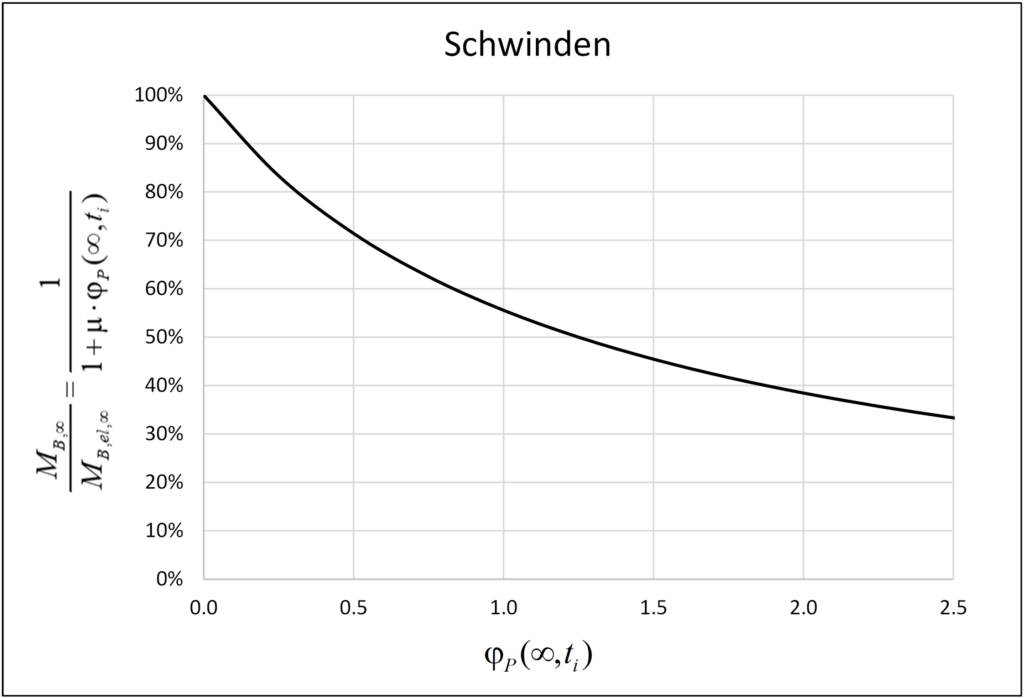
Abbildung 7. *M_B,∞* zu *M_B,el,∞* Verhältnis (μ=0.80)

Das Biegemoment M_B(t) am Pfeilerkopf infolge Schwinden wächst mit der Zeit an, bis es zur Zeit t = ∞ein maximales Biegemoment M_B,∞ erreicht (siehe Abbildung 4(b)), das das 1/(1+μ·φ_P(∞,t_i)) fache des elastischen Biegemoments M_B,el,∞infolge der kurzfristigen Wirkung des Gesamtschwindens ε_cs_,∞ beträgt.

Das maximale Biegemoment M_B,∞am Pfeilerkopf zur Zeit t = ∞, das unabhängig vom Kriechkoeffizienten φ_G(∞,t_i) des Trägers ist, ist gleich 38%·M_B,el,∞für einen typischen Wert von φ_P(∞,t_i) = 2.0. Aus diesem Grund berücksichtigen viele Ingenieure 40% des Gesamtschwindens (40%·φ_cs_,∞), um die Schnittgrössen in den Pfeilern zur Zeit t = ∞ aufgrund von Langzeiteinflüssen zu bestimmen. Da die Pfeiler jedoch vor dem Träger gebaut werden, ist der Pfeilerkriechkoeffizient im Betonalter, in dem der Träger zu schwinden beginnt, oft kleiner als 2.0 und in Regionen mit hoher relativer Luftfeuchtigkeit ohnehin kleiner (z. B. φ_P(∞,t₀) ≈ 1.8 für C30/37 und RH ≈ 80%, wie in der Schweiz üblich). Wird darüber hinaus die vorteilhafte Wirkung eines gerissenen Pfeilers mit entsprechend reduzierter Steifigkeit berücksichtigt, muss ein noch geringerer äquivalenter Kriechkoeffizient φ_P (ermittelt z.B. aus einer Querschnittsanalyse als Verhältnis der Krümmungen mit und ohne Kriechen) verwendet werden. Wenn die Ingenieure nicht über diesen Hintergrund verfügen und wahllos den Referenzwert von 40% (φ_P(∞,t_i) = 2.0) oder sogar einen reduzierten Wert für das Schwinden aufgrund der hohen Luftfeuchtigkeit verwenden, kann der Entwurf der Pfeiler auf der unsicheren Seite liegen, insbesondere bei GZG. Betrachtet man beispielsweise einen Pfeiler-Kriechkoeffizienten zur Zeit t = ∞ von φ_P(∞,t_i) = 1.25 ab dem Zeitpunkt, an dem der Träger zu schwinden beginnt, so beträgt das Biegemoment am Pfeilerkopf M_B,∞ =50%·M_B,el,∞, d.h. 32% höher als M_B,∞ =38%·M_B,el,∞für φ_P(∞,t_i) = 2.0.

Vorspannung:

Das Biegemoment M_B,∞ am Pfeilerkopf zur Zeit t = ∞ infolge der Vorspannung (einschliesslich kurz- und langfristigen Einflüssen) beträgt:

${{M}_{B,\infty }}={{M}_{B,el}}({{t}_{0}})\cdot \left( 1+\frac{{{\varphi }_{G}}(\infty ,{{t}_{j}})-{{\varphi }_{P}}(\infty ,{{t}_{i}})+\frac{\Delta {{P}_{\infty }}}{P({{t}_{0}})}}{1+\mu \cdot {{\varphi }_{P}}(\infty ,{{t}_{i}})} \right)$

wobei t_j und t_i das Betonalter des Trägers bzw. des Pfeilers bei Einwirkung der Vorspannung sind.

Abbildung 8 zeigt das Verhältnis zwischen dem Biegemomentzuwachs ΔM_B,∞ und dem anfänglichen elastischen Biegemoment M_B,el(t₀) am Pfeilerkopf zur Zeit t = ∞. Wie bei der Bemessung häufig angenommen, wirkt das Kriechen des Pfeilers zusammen mit dem (negativen) Beitrag der Vorspannungsverluste dem Anstieg der Biegemomente am Pfeilerkopf, der durch das Kriechen des Trägers verursacht wird, entgegen und kompensiert ihn bei bestimmten Werten der Kriechkoeffizienten sogar. In typischen Fällen sind jedoch erhebliche Unterschiede zu beobachten. Im Allgemeinen ist das Verhältnis ΔM_B,∞ / M_B,el(t₀) eine Funktion des Pfeiler-Kriechbeiwerts φ_P(∞,t_i), des Träger-Kriechbeiwerts φ_G(∞,t_j), der Vorspannkraftverluste ΔP_∞/P(t₀) und des Alterungsbeiwerts μ. Die in Abbildung 8 dargestellten Kurven wurden für μ=0.80, φ_G(∞,t_j) = {1.0; 1.5; 2.0} und ΔP_∞/P(t₀)= {0%; 10%} erstellt. Man kann feststellen, dass die Vorspannkraftverluste eine geringe Auswirkung auf das Verhältnis ΔM_B,∞/ M_B,el(t₀) haben (etwa 5 % für die verwendeten Parameter), was in den Berechnungen vernachlässigt werden kann.

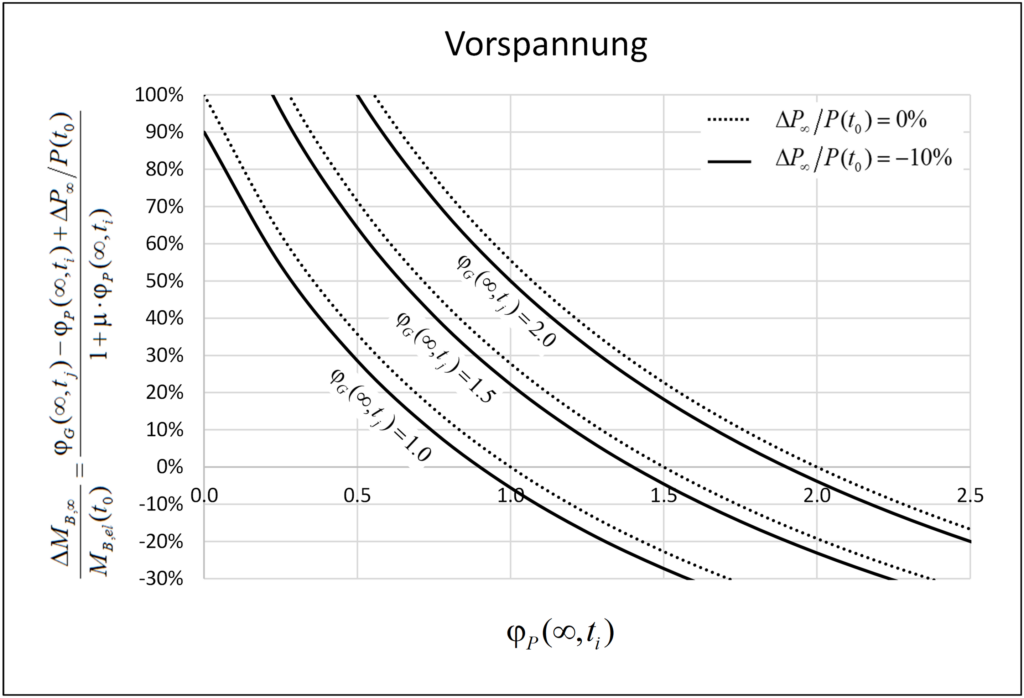
Abbildung 8. Δ*M_B,∞* zu *M_B,el*(t₀) Verhältnis (μ=0.80, φ_G(∞,*t_j*) = 1.0-1.5-2.0 und Δ*P_∞*/P(t₀)=0%-10%). Δ*M_B*_,∞: Biegemomentenzuwachs am Pfeilerkopf infolge langfristiger Vorspannungseffekte zur Zeit t = ∞; M_B,el(t₀): Anfängliches elastisches Biegemoment am Pfeilerkopf infolge der Vorspannung

Das Verhältnis ΔM_B,∞/ M_B,el(t₀) hängt von den Kriechkoeffizienten des Trägers und des Pfeilers (mit t_i und t_j = Betonalter dieser Elemente zum Zeitpunkt des Aufbringens der Vorspannung) sowie von den Vorspannungsverlusten ab. Das anfängliche Biegemoment M_B,el(t₀) am Pfeilerkopf nimmt im Laufe der Zeit ab, wenn der Kriechkoeffizient des Pfeilers φ_P(∞,t_i) höher ist als der Kriechkoeffizient des Trägers φ_G(∞,t_j), d. h. φ_P(∞,t_i) > φ_G(∞,t_j), und nimmt andernfalls zu (unter Vernachlässigung der Vorspannungsverluste), was typischerweise zutrifft, da die Pfeiler vor den Trägern gebaut werden.

Bei einem Pfeiler-Kriechkoeffizienten von φ_P(∞,t_i) = 1.25 erhöht sich das Biegemomentinkrement ΔM_B,∞zur Zeit t = ∞ um etwa 10 % bzw. 35 % gegenüber dem anfänglichen Biegemoment M_B,el(t₀) für Träger-Kriechkoeffizienten von φ_G(∞,t_j) = 1.5 bzw. φ_G(∞,t_j) = 2.0. Ein Anstieg von 35 % ist nicht von vornherein vernachlässigbar; er kann jedoch für niedrige und mittlere Vorspannungsniveaus des Trägers vernachlässigt werden, da der Biegemomentenzuwachs ΔM_B,∞ im Vergleich zu dem durch Schwinden verursachten Biegemoment in der Regel gering ist.

4. Schlussfolgerungen

Für eine vorläufige Bemessung (Abschätzung der inneren Einwirkung) von Pfeilern, die monolithisch mit einem vorgespannten Träger verbunden sind, ist es eine gültige Näherung, 40…50 % des Gesamtschwindens zur Zeit t = ∞ ε_cs_,∞ zu berücksichtigen und die über die Zeit zunehmende innere Kraft infolge der Vorspannung zu vernachlässigen. Diese Überlegungen können auch bei der Detailplanung akzeptabel sein, wenn die Bemessung der Pfeiler nicht entscheidend ist und der Planer den Einfluss der Langzeiteinflüsse auf das Bauwerk, einschliesslich des Bauprozesses, kontrollieren kann. Im Allgemeinen kann jedoch die Verwendung eines Wertes von 40%·ε_cs_,∞ zur Berücksichtigung der langfristigen Auswirkungen unsicher sein, da die in den Pfeilern wirkenden Schnittgrössen unterschätzt werden.

Die vorgestellten Gleichungen zur Abschätzung der Schnittgrössen in den Pfeilern aufgrund der Langzeiteinflüsse sind in der Ingenieurpraxis nützlich. Sie ermöglichen eine einfache, aber wesentlich genauere Langzeitanalyse, wie sie für lange fugenlose Bauwerke mit monolithischen Pfeiler-Träger-Verbindungen erforderlich ist. Darüber hinaus kann eine geeignete Strategie der Betonierabschnitte dazu beitragen, die Länge von fugenlosen Bauwerken deutlich zu erhöhen.

Abschliessend wird darauf hingewiesen, dass die durch Schwinden und Vorspannung verursachten Momente an den Pfeilerköpfen aufgrund des Kriechens der Pfeiler zwar reduziert werden, dass aber bei der Bemessung von Lagern und Dehnungsfugen und der Abschätzung von Brückenendverschiebungen in integralen Widerlagern die vollen Trägerverschiebungen berücksichtigt werden müssen.

Ich hoffe, dass dieser Beitrag für Sie von Interesse und Nutzen war. Wir freuen uns über Kommentare und Anregungen.

Alejandro Giraldo Soto

Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram