Grammatik für Fachwerkmodelle erklärt – Concrete E-Learning Platform

Link to English version: Grammars for Strut-and-Tie Models Explained

Fachwerkmodelle dienen im Stahlbetonbau häufig als vereinfachte, sichere und meist händische Entwurfsmethode für Balken oder Wände. Um ein Fachwerkmodell herzuleiten brauchen Ingenieur:innen meist viel Zeit und Fachwissen, weshalb sich Forscher:innen seit Jahrzehnten mit anderen Möglichkeiten für die Fachwerkgenerierung beschäftigen. In meinem letzten Blogpost, habe ich die zwei Hauptansätze zur automatisierten Generierung von Fachwerkmodellen für Stahlbetontragwerke und ihre Vor- und Nachteile vorgestellt. Die kontinuierliche Topologieoptimierung hat das Ziel, möglichst viel Material zu entfernen, um die Masse oder das Volumen einer Struktur zu minimieren, während gleichzeitig strukturelle Bedingungen (z.B. Fliessgrenze der Bewehrungsstäbe) erfüllt werden müssen. Daraus muss dann ein Fachwerk abgeleitet werden. Bei dieser Methode ist es jedoch schwierig, ausführungstechnische Aspekte (z.B. Präferenz für eine regelmässige Anordnung der Bewehrung oder orthogonale Bewehrung) adequat zu berücksichtigen. Die diskrete Layoutoptimierung zielt darauf ab, eine verbundene Struktur auf Grundlage vordefinierter gitterartiger Knotenpunkte unter bestimmten strukturellen Bedingungen zu finden. Diese Methode hat jedoch Schwierigkeiten, benutzerspezifische Anpassungen zu berücksichten. Aufgrund dieser Nachteile konnten sich beide Methoden bisher noch nicht in der Praxis durchsetzen.

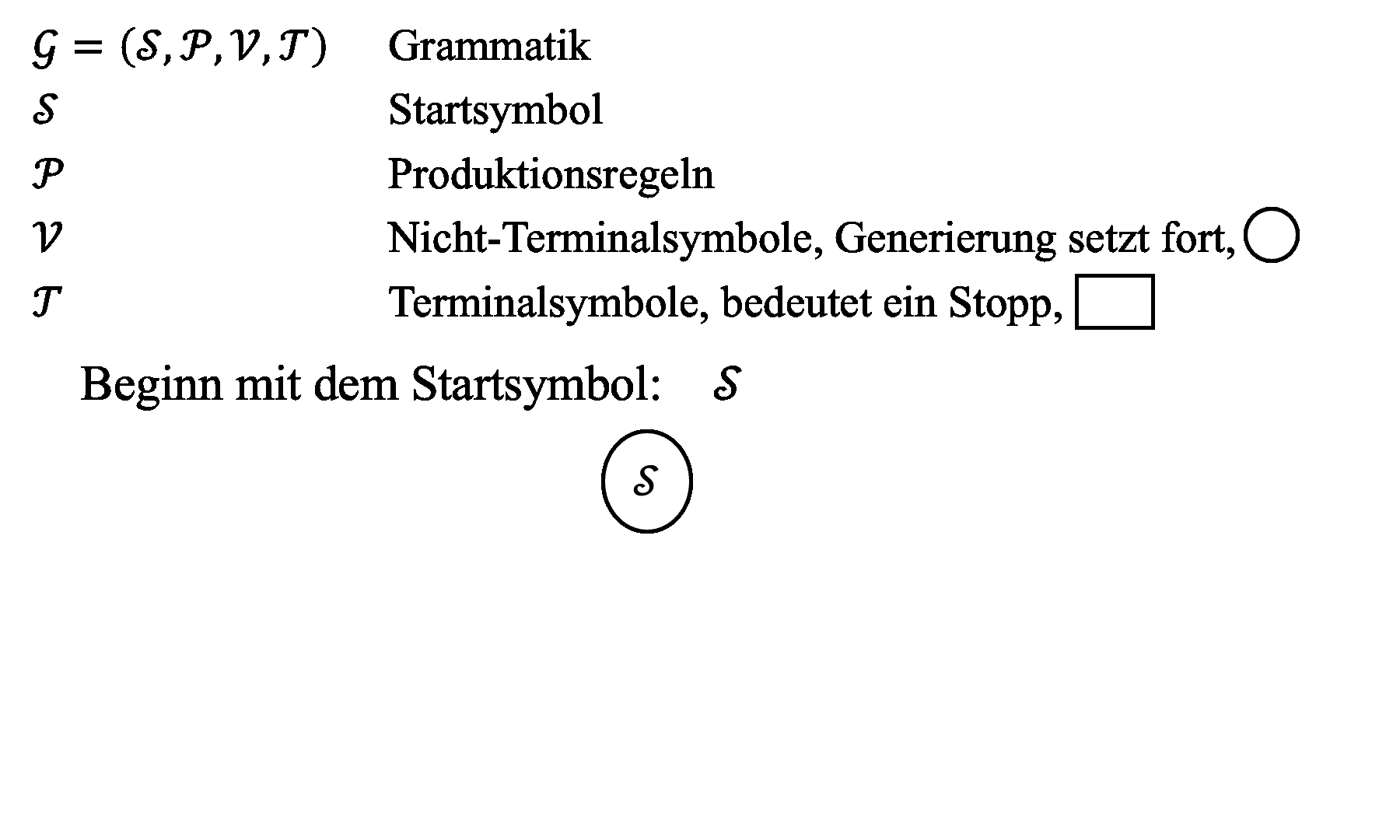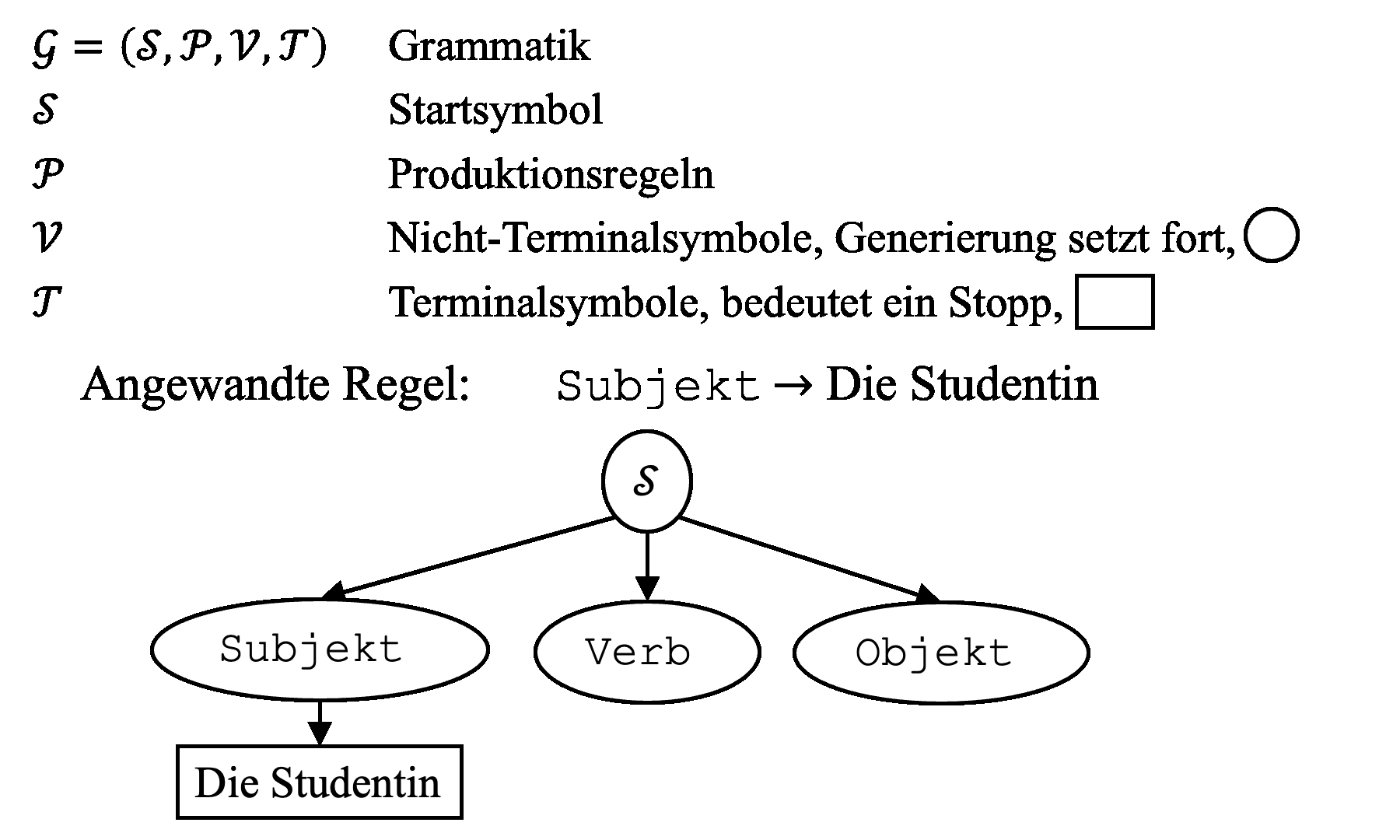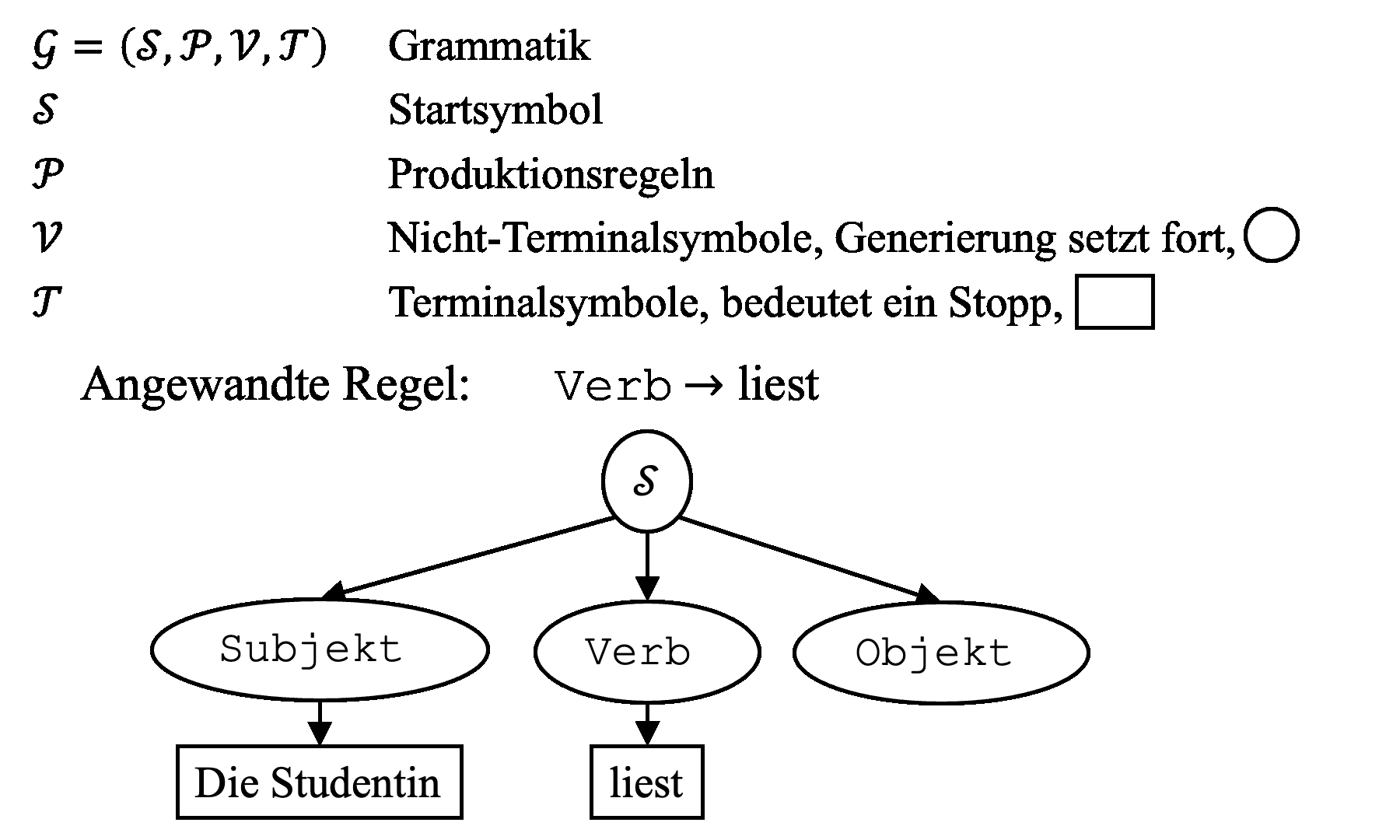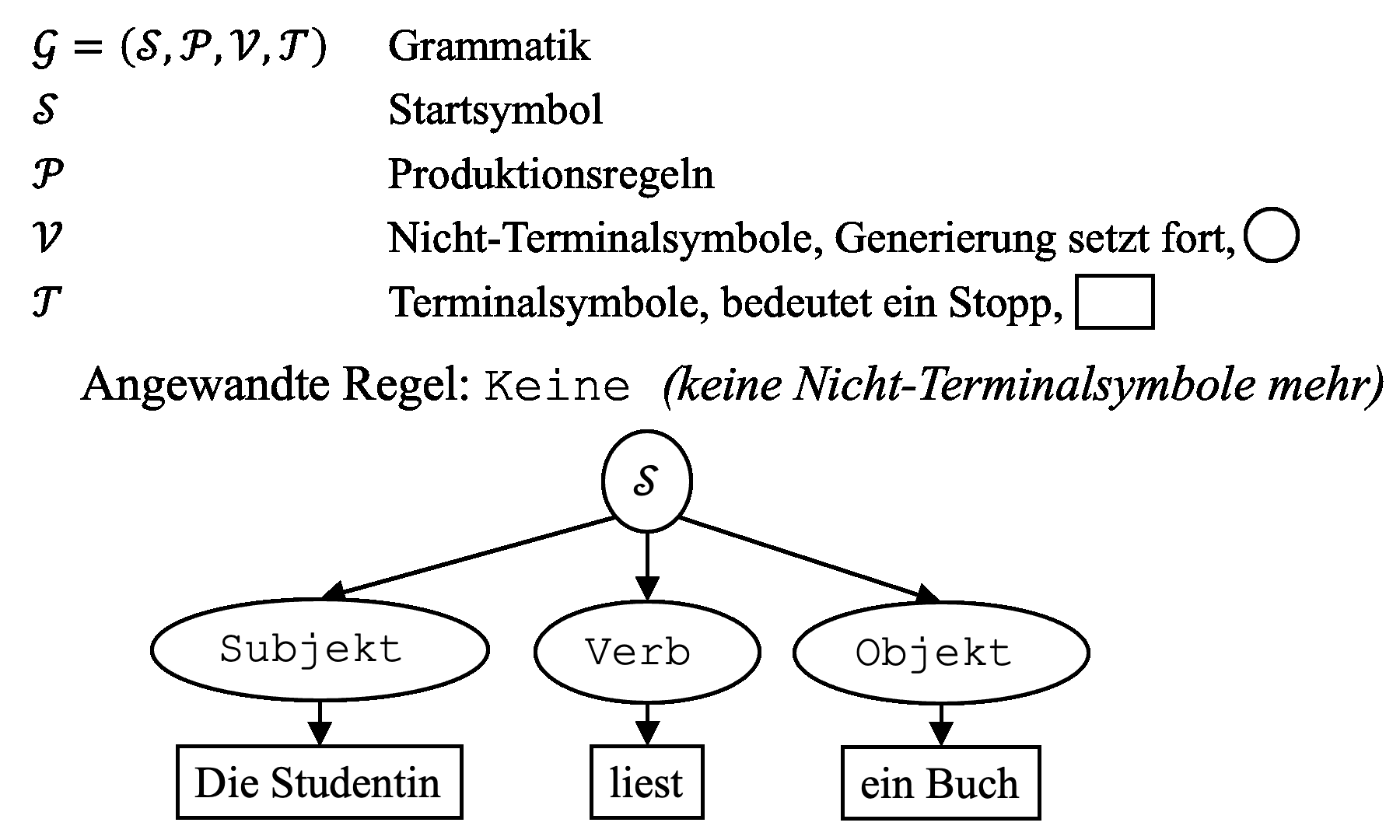
Um diese Forschungslücke anzugehen, haben wir einen Ansatz basierend auf Regeln und Grammatik entwickelt. Inspiriert von der theoretischen Informatik und formalen Sprachen, wurde das Konzept der Grammatik bereits auf Design-, Architektur- und Ingenieursanwendungen übertragen. Fachwissen und Präferenzen können somit in die Regeln integriert werden, die unterschiedliche Designs generieren können. Zuerst möchten wir dieses Konzept anhand eines einfachen Beispiels aus der formalen Sprache veranschaulichen. Sogenannte kontextfreie Grammatiken bestehen aus den Symbolen S (Startsymbol), P (Satz an Produktionsregeln), T (Terminalsymbole, Generierung stoppt; hier mit einem Rechteck dargestellt) und V (Nichtterminalsymbole, Generierung geht weiter; hier mit einer Ellipse dargestellt), siehe Abb. 1. Angenommen wir wollen einen Satz generieren, dann muss jede rechte Seite einer Regel im Generierungsprozess ein Nichtterminalsymbol (linke Seite der Regel) ersetzen. Wir beginnen mit der Regel S → Subjekt-Verb-Objekt. Als nächste Regeln ersetzen wir Subjekt durch «Die Studentin» usw. bis wir keine Nichtterminalsymbole mehr übrig haben und den Satz «Die Studentin liest ein Buch» gebildet haben.

Abbildung 1: Ein anschauliches Beispiel für die Generierung des Satzes «Die Studentin liest ein Buch» mit einer kontextfreien Grammatik.

Dieses Konzept wurde auch im generativen Design angewendet. Unsere Forschungsinteressen lagen dabei hauptsächlich darin, ob man mit einem solchen Ansatz Fachwerkmodelle generieren kann und ob diese generierten Fachwerkmodelle praktischer als optimierungsbasierte Vorschläge sind.

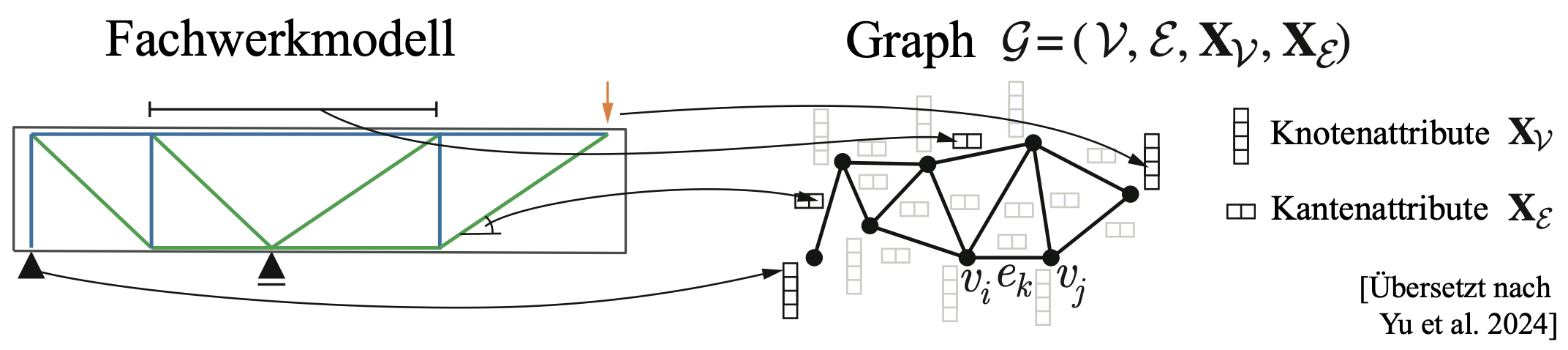
Abbildung 2: Repräsentierung eines Fachwerkmodells als Graph [1].

Als erster Schritt, wird das statische Problem als Graph dargestellt (Abb. 2). Wir sind normalerweise mit euklidischen Daten vertraut, welche man in Matrixform darstellen kann. Wenn wir jedoch komplexere Zusammenhänge von Daten (z.B. hierarchische Strukturen oder Abhängigkeiten) erfassen möchten, können wir nicht-euklidische Darstellungen wie Graphen, Gruppen oder Zellen verwenden. Darunter sind Graphen für uns vorteilshaft, da sie strukturierte Daten mittels Knoten und Kanten effizient darstellen können. Demnach kann man ein Fachwerkmodell einfach in eine Graphrepräsentierung umwandeln, indem die Knoten des Fachwerkes die Knoten des Graphen werden und die Druck- und Zugstäbe die Kanten. Dadurch erhalten wir einen Graph mit den gleichen Verbindungen wie das Fachwerk. Jedoch können wir aufgrund der Graphrepräsentierung nicht mehr die typische matrixbasierte statische Berechnungsmethode anwenden, um die Kräfte der Kanten zu erhalten. Darum verwenden wir die Gleichgewichtsbedingunen in den Knoten, um das statische Gleichgewicht zu finden. Für die computergestütze Implementierung, kann man zusätzliche Informationen wie Länge und Winkel einer Kante als Knoten- oder Kantenattribute hinzufügen.

Die Hauptschwierigkeit des grammatikbasierten Ansatzes besteht in der Herleitung der Regeln. Der Satz an Regeln sollte allgemein genug sein, um eine Vielzahl von verschiedenen Fachwerkmodelle zu generieren, aber auch spezifisch genug, um bestimmte bauliche und ingenieurtechnische Einschränkungen zu berücksichtigen, wie z.B. die Einhaltung von Mindestfachwerkwinkeln. Um diese Regeln herzuleiten, ist demnach ein gewisses geometrisches und statisches Verständnis erforderlich. Einzelheiten zu solchen Regeln finden Sie in unserem kürzlich veröffentlichten Fachzeitschriftenartikel [1], wovon einige Beispiele in Abb. 3.

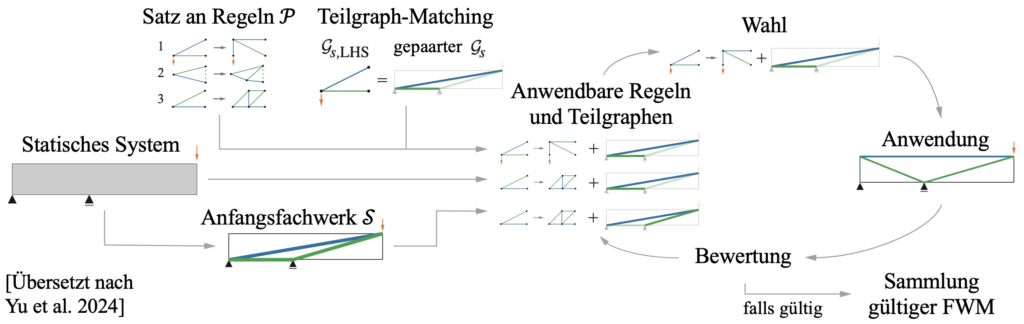
Abbildung 3: Konzept der Grammatik für die Generierung von Fachwerkmodellen [1].

Sobald die Regeln definiert sind, folgt das Verfahren zur Generierung der Fachwerkmodelle demselben Vorgehen zur Generierung von Sätzen, siehe Abb. 3. Ein Anfangsfachwerk (das Startsymbol) kann aus dem statischen Problem abgeleitet werden, z.B. indem die Randbedingungen miteinander verbunden werden. Im Gegensatz zur formalen Sprache, hat dieser Ansatz jedoch keine direkten Terminal- und Nichtterminalsymbole. Kanten können als Terminalsymbole festgelegt werden, um die Anzahl möglicher Generierungen zu reduzieren. Andererseits, erkennt ein Teilgraph-Matching-Algorithmus¹, basierend auf dem Satz der Produktionsregeln, welche linken Seiten der Regeln im aktuellen Fachwerk gefunden werden können. Diese möglichen Kombinationen werden dem Benutzer oder der Benutzerin vorgeschlagen, welche:r dann die nächste Regel auswählen kann. Nach der Transformation des Fachwerkes mit der gewählten Regel werden einige Kennzahlen zur Beurteilung der Qualität des Fachwerks angezeigt. Diese Kennzahlen beziehen sich sowohl auf die Gültigkeit (z.B. Geometrie, Überkreuzung von Kanten und Fachwerkwinkel) als auch auf die Eignung (z.B. Komplexität der Bewehrung und Stahlverbrauch) von Fachwerkmodellen.

Die Generierung von Fachwerken mit Grammatiken wird anhand des Beispiels einer Wand mit einer Öffnung in Abb. 4 veranschaulicht, welches ein übliches Beispiel² aus der Literatur ist. Zuerst wenden wir eine Regel an, welche den linken Lagerknoten über der Öffnung aufhängt. Die Parameter der Regel können angepasst werden, um die Position des neu eingeführten Knotens zu beeinflussen (vergleichen Sie den ersten Schritt jeder Lösung). Durch Variieren von Regeln und Parametern können unterschiedliche Fachwerkmodelle generiert werden. Sowohl ein einfacher und effizienter Entwurf, wie Lösung A, mit geneigter Bewehrung, wie auch ein komplexerer Entwurf (Lösung C) mit orthogonaler Bewehrung können so also mit dem grammatikbasierten Ansatz generiert werden.

Abbildung 4: Ein Beispiel der grammatikbasierten Generierung von drei Fachwerkmodellen für eine Wand mit einer Öffnung [1].

Diese und weitere Beispiele [1] zeigen, dass die grammatikbasierte Generierung es erlaubt, mittels Mensch-Computer Interaktion praktischere Fachwerkmodelle als mittels optimierungsbasierten Methoden³ zu generieren. Diese Generierung könnte jedoch mit zunehmender Komplexität des Fachwerks und der Anzahl Regeln umständlich werden. Derzeit erforschen wir deshalb alternative rechnergestütze oder KI-basierte Methoden, um den Entwurfsraum automatisierter navigieren zu können, und hoffen, Sie im Verlaufe des Jahres über Fortschritte informieren zu können. Bei Fragen oder Anmerkungen, können Sie gerne Karin Yu kontaktieren.

Karin Yu

Literatur

[1] Yu, K. L., Kraus, M. A., Chatzi, E., Kaufmann W. (2024). Grammar-Based Generation of Strut-and-Tie Models for Designing Reinforced Concrete Structures. Computers & Structures. Volume 305. 107549. doi.org/10.1016/j.compstruc.2024.107549