Link to the English version: Developing a material model for reinforced concrete structures subjected to cyclic loading
An der Professur für Massiv- und Brückenbau setzen wir seit einigen Jahren ein selbst entwickeltes Materialmodell für Simulationen von Stahlbetonstrukturen ein, unter anderem für Nachrechnungen von bestehenden SBB Rahmenbrücken. Die Simulationen werden auch nicht-lineare Finite-Elemente (NLFE) Analysen genannt. Mehr über den Begriff “NLFE Analysen” können Sie im Blogbeitrag “Die Finite-Elemente-Methode im konstruktiven Ingenieurbau” lesen. Wie in diesem beschrieben wird, besteht das Grundprinzip von FE Analysen in der Tragwerksplanung darin, eine komplexe Tragstruktur in viele Elemente zu unterteilen (Diskretisierung) und die Elemente mathematisch zu einem Gesamtmodell zu verknüpfen. Für eine FE Analyse wird neben der Geometrie der Tragstruktur, der Einwirkung und den Randbedingungen/Lagerung auch ein Materialmodell benötigt, um (auf der Elementebene, präziser gesagt im Integrationspunkt) aus den Verformungen, resp. Dehnungen, die zugehörige Kraft, resp. Spannung zu berechnen. Das an unserer Professur verwendete nicht-lineare Materialmodell, genannt CMM-Usermat, simuliert die Steifigkeiten (= Kraft / Verformung resp. = Spannungen / Dehnungen) von Scheiben-, Platten und Schalenelementen akkurat, und die in Versuchen beobachteten Verformungen, Versagensarten und Maximallasten werden vom Modell im Allgemeinen gut abgebildet. Für einen vertieften Einblick in den Aufbau und Verifikation des Materialmodelles verweise ich auf folgende Literatur: [1]–[4]. Das CMM-Usermat ist zurzeit auf unidirektionale Belastungen beschränkt, d.h. es können nur monoton ansteigende Belastungen berücksichtigt werden; Ent- und Wiederbelastungen können nicht simuliert werden.
Als logischer nächster Schritt in der Entwicklung des Materialmodelles soll es verallgemeinert werden, damit Ent- und Wiederbelastungen / zyklische Belastungen aufgebracht werden können. Dies ermöglicht es uns, Simulationen der Tragstrukturen für verschiedene Zeitpunkte der zyklischen Belastung (z.B. bei einem Erdbeben) durchzuführen, auch bezeichnet als Zeitverlaufsanalyse. In meinem Doktorat befasse ich mich mit dieser Weiterentwicklung des Materialmodelles. Ziel des Forschungsprojektes ist es, mit dem zu entwickelnden zyklisches Materialmodell stabile und zuverlässige FE Analysen durchzuführen, die das Tragverhalten von zyklisch beanspruchten Stahlbetonstrukturen möglichst exakt wiedergeben. Caminada hat sich im Rahmen von seinem Masterstudium an der Hochschule Luzern (HSLU) bereits dieser Thematik angenommen und vielversprechende Resultate erzielt [5]-[7], die eine vertiefte Erforschung rechtfertigen.
Finanzierung des Forschungsprojektes:
Das in diesem Blogbeitrag beschriebene Forschungsprojekt, das auf drei Jahre ausgelegt ist und 2025 endet, wird vom Eidgenössischen Nuklearsicherheitsinspektorat (ENSI) finanziert und von seinen Fachexpert:innen begleitet. Ein Forschungsschwerpunkt des ENSIs liegt bei der Erdbebenanalyse von Stahlbetontragwerken mit dominanter Scheibentragwirkung (Schubwände). Mit den Erkenntnissen aus diesem Projekt sichert das ENSI seine Kompetenz bei der Bewertung der Tragsicherheit solcher Tragelemente. Weitere Informationen zur Forschung des ENSI findet man im jährlich erscheinenden Erfahrungs- und Forschungsbericht.
In der Folge wird der Aufbau des zyklischen Materialmodelles beschrieben, wobei CMM-Usermat-U bzw. CMM-Usermat-C das unidirektionale bzw. zyklische Materialmodell bezeichnet.
Stahlbeton in a nutshell (für Nicht-Bauingenieur:innen):
Beton hält einer relativ hohen Druckbelastung stand, aber wenn er auf Zug beansprucht wird, ist die maximal aufnehmbare Last eine Grössenordnung kleiner, wobei das Versagen auch noch spröde ist. Die tiefe und stark streuende Betonzugfestigkeit wird daher meist vernachlässigt bei der Bemessung der Tragsicherheit. Beton wird jedoch mindestens in zwei Richtungen (normalerweise senkrecht zueinander) mit duktilem Stahlstäben (Bewehrung), die im Vergleich zu Beton eine sehr hohe Zugfestigkeit aufweisen, verstärkt. Die Kombination von Beton und Bewehrung führt zum charakteristischen Tragverhalten von Stahlbeton: Zugkräfte werden von der Bewehrung übernommen (nachdem der Beton gerissen ist) und Druckkräfte werden überwiegend vom Beton abgetragen.
Wie dieser kurzen Beschreibung der Bestandteile und des Tragverhaltens zu entnehmen ist, kann Stahlbeton nicht als homogenes isotropes Material betrachtet werden. Das Zusammenwirken der Bewehrungsstäbe mit dem umhüllenden Beton ist sehr komplex und daher erfordert die Modellierung gewisse Vereinfachungen.
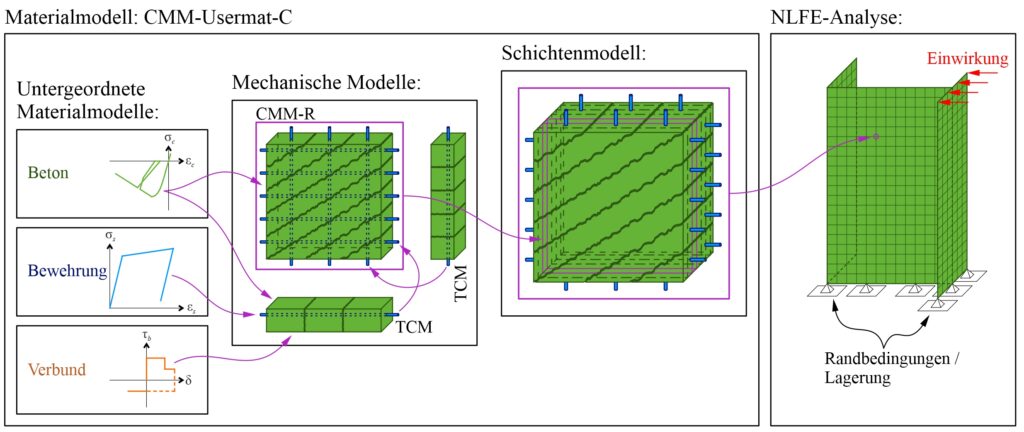
Um eine gute Näherungslösung für das komplexe Stahlbetontragverhalten zu erhalten, wurde beim CMM-Usermat-C ein Ansatz gewählt, der in drei Ebenen gegliedert werden kann: Untergeordnete Materialmodelle, mechanische Modelle und Schichtenmodell (siehe Abbildung 1).
Die untergeordneten Materialmodelle beschreiben die Spannungs-Dehnungsbeziehungen der Stahlbetonkomponenten (Beton und Bewehrung) sowie die Verbundspannungs-Schlupfbeziehung zwischen Beton und Bewehrung. Eine Bibliothek von verschiedenen untergeordneten Materialmodellen für Beton, Bewehrung und Verbund wird zurzeit aufgebaut.
Die mechanischen Modelle, die das Herzstück des CMM-Usermat-C darstellen, abstrahieren das Tragverhalten von Stahlbetonelementen so, dass die wesentlichen Mechanismen, unter anderem das Zusammenwirken der Stahlbetonkomponenten, abgebildet werden. Der Fokus liegt dabei auf einer mechanisch konsistenten Modellierung, bei der das Gleichgewicht der Kräfte und die Kompatibilität (Dehnungen und Spannungen stimmen in jedem Punkt mit den beschriebenen untergeordneten Materialmodellen für Bewehrung und Beton überein) erfüllt sind. Konkret basiert das CMM-Usermat-C auf dem Zuggurtmodell [8] (auf Englisch: Tension Chord Model (TCM)), welches die Mitwirkung des Betons zwischen den Rissen (Zugversteifung) mitberücksichtig und dem Gerissenen Scheibenmodell mit frei rotierenden Rissen [9] (auf Englisch: Cracked Membrane Model with rotating, stress-free cracks (CMM-R)), das den Lastabtrag von primär auf Schub belasteten Scheiben modelliert. Das TCM und das CMM-R greifen für das Materialverhalten der Komponenten auf die Bibliothek der untergeordneten Materialmodelle zurück. Nebenbemerkung: Der Name des Materialmodelles CMM-Usermat-C leitet sich vom verwendeten mechanischen Modell CMM-R ab, wobei «Usermat» für «user-defined material» steht.
Die dritte und höchste Ebene im CMM-Usermat-C bildet das Schichtenmodell [10], das für die Erweiterung von den bisher diskutierten mechanischen Modellen (1D und 2D) zu dreidimensionalen Platten- oder Schalenelementen zuständig ist. Dabei wird das Schalen- oder Plattenelement in Schichten unterteilt, wobei für jede Schicht ein ebener Spannungszustand angenommen wird. Die einzelnen Schichten können mit den oben beschriebenen mechanischen Modellen simuliert werden. Alle resultierenden Kräfte in den Schichten werden addiert/integriert und ergeben schlussendlich die allgemeine Beanspruchung (Membrankräfte, Biegung und Drillung) an einem bestimmten Punkt im FE-Netz.
Nachdem der gesamte Aufbau des CMM-Usermat-C erklärt wurde, beschreiben die beiden nächsten Abschnitten die konkrete Erweiterung des TCM auf zyklische Belastungen und die Verifikation des TCM für zyklische Belastungen anhand von Nachrechnungen eines zyklisch belasteten Zuggurtversuches.
Erweiterung des TCM auf zyklische Belastungen
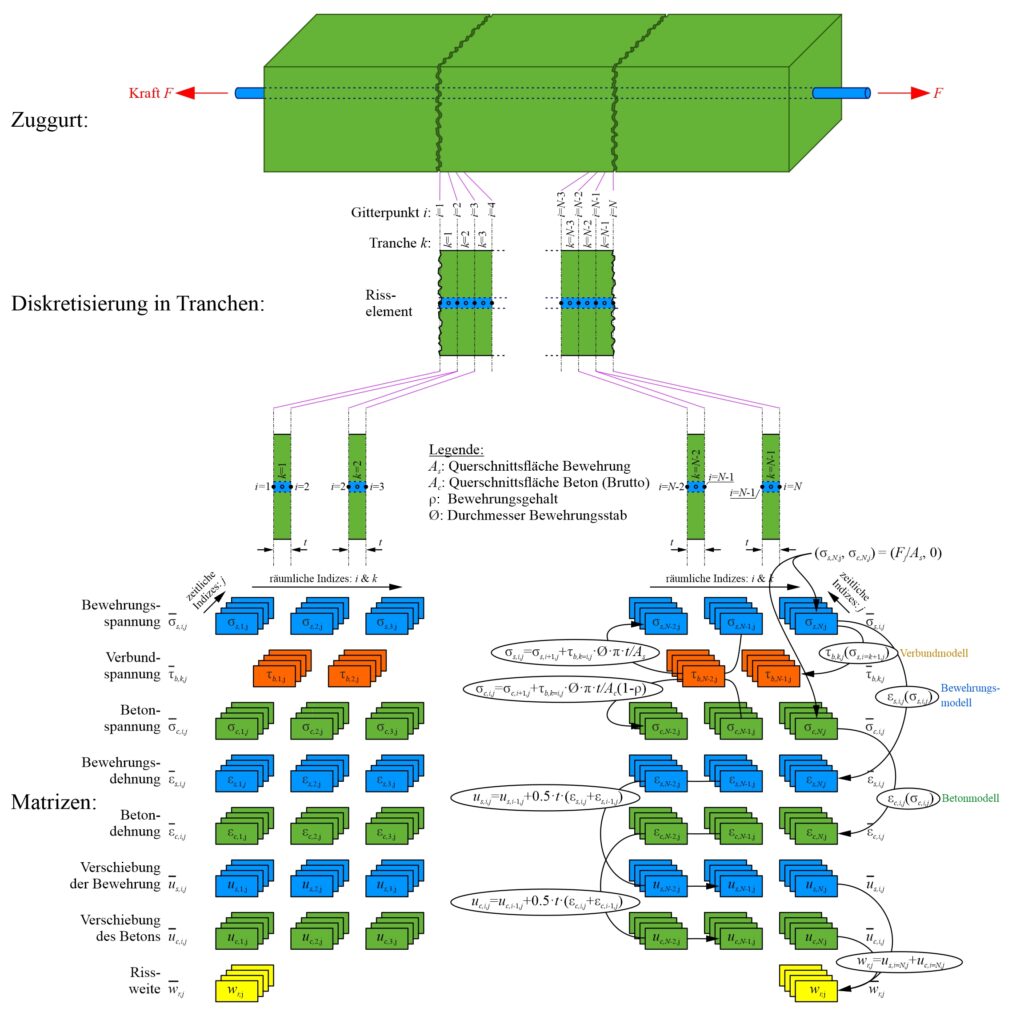
Das TCM wird im CMM-Usermat-C gebraucht, um die Beziehung zwischen durchschnittlicher Längsdehnung und Stahlspannung am Riss für ein auf Zug belastetes 1D-Stahlbetonelement zu simulieren. Eine analytische Lösung für die Beziehung zwischen durchschnittlicher Längsdehnung und Stahlspannung am Riss, wie sie für unidirektionale Belastung (CMM-Usermat-U) verwendet wird, ist bei zyklischen Beanspruchungen, angesichts der unendlichen Anzahl möglicher Lastverläufe, schwierig zu erreichen. Daher wurde eine algorithmische Lösung implementiert, in der der 1D-Zuggurt in endliche Tranchen unterteilt und Spannungen, Dehnungen und Verschiebungen in der Bewehrung und im Beton Tranche für Tranche berechnet werden (siehe Abbildung 2). Es wird angenommen, dass die Verbundschubspannung über die Dicke der Tranchen konstant ist. Alle Variablen (σs, σc, εs, εc, us, uc, wr) ausser der Verbundschubspannung (τb) werden an den Gitterpunkten zwischen zwei benachbarten Tranchen ausgewertet. Anhand von Gleichgewichtsüberlegungen können die Spannungen in der Bewehrung, dem Beton und die Verbundschubspannungen bestimmt werden. Mit den untergeordneten Materialmodellen können die berechneten Spannungen in der Bewehrung (σs,i) oder im Beton (σc,i) am Gitterpunkt i mit den Dehnungen (εs,i, εc,i) oder Verbundspannungen (τb,k) in Beziehung gesetzt werden.
Verifikation des TCM für zyklische Belastungen
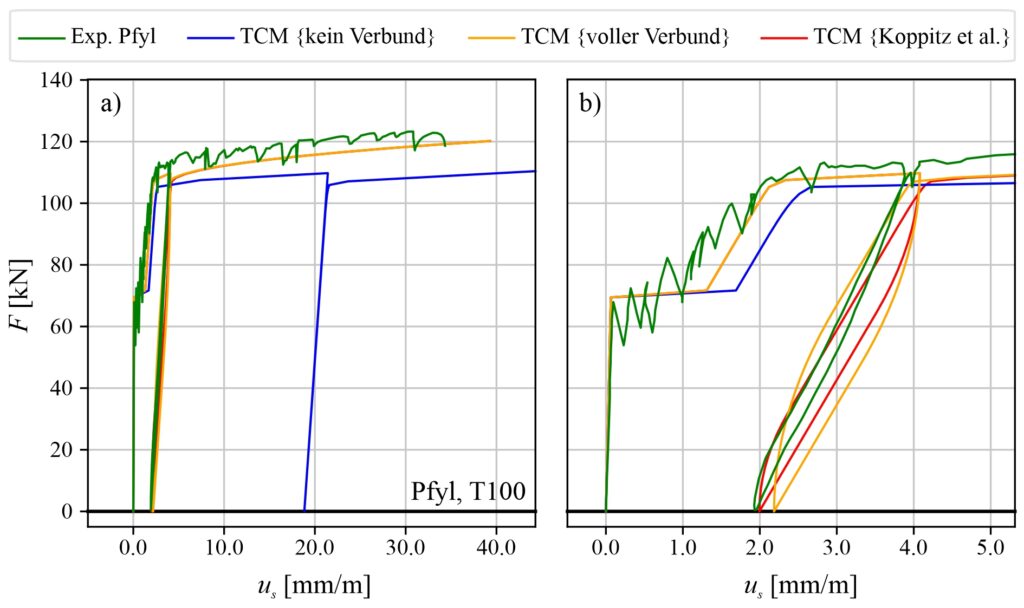
Mit dem in Python implementierten Algorithmus des zyklischen TCM können Zugversuche an Stahlbetonelementen simuliert werden. Die Ergebnisse von drei Simulationen und einem von Pfyl [11] durchgeführten Versuch sind in Abbildung 3 dargestellt. Der Stahlbeton-Zuggurt wird belastet, bis sich Risse bilden. Nach einem weiteren Lastanstieg überschreitet die Bewehrung die Fliessgrenze. Die Last wird danach auf null reduziert und wieder erhöht, bis das Versagen erreicht ist. Abbildung 3 zeigt, dass die TCM-Simulationen das Gesamtverhalten gut wiedergeben, wobei es erhebliche Unterschiede zwischen den Verbundmodellen {voller Verbund; Koppitz et al. [12]} und {kein Verbund} gibt. Letzteres berücksichtigt die Zugversteifung im gerissenen elastischen Bereich nicht und überschätzt die Verformungen im plastischen Bereich. Die TCM-Simulationen mit den Verbundmodellen {voller Verbund; Koppitz et al. [12]} überschätzen die Energiedissipation während der Ent- und Wiederbelastung (Hystereseschleife), wobei das Verbundmodell {Koppitz et al. [12]}, das eine Verbundschädigung nach dem ersten Lastwechsel berücksichtigt, weniger von der experimentellen Kurve abweicht als das Verbundmodelle {voller Verbund}. Die Ergebnisse der Simulationen sind im Allgemeinen zufriedenstellend.
Weitere Beschreibungen und Ergebnisse werden folgen, sobald das Projekt weiter fortgeschritten ist.
Simon Karrer
Literatur
[1] P. Roos, “FEM Modelle für Stahlbetonplatten – Verifizierung des Schichtenmodells anhand von Bauteilversuchen”, Hochschule Luzern Technik & Architektur, Horw, 2014.
[2] K. Thoma, P. Roos, and M. Weber, “Finite-Elemente-Analyse von Stahlbetonbauteilen im ebenen Spannungszustand”, Beton- und Stahlbetonbau, vol. 109, no. 4, pp. 275–283, 2014, doi: 10.1002/best.201300087.
[3] K. Thoma, P. Roos, and G. Borkowski, “Finite Elemente Analyse von Stahlbetonplatten”, Beton- und Stahlbetonbau, vol. 109, no. 12, pp. 895–904, 2014, doi:10.1002/best.201400047.
[4] K. Thoma, “Finite element analysis of experimentally tested RC and PC beams using the cracked membrane model”, Engineering Structures, vol. 167, no. 15, pp. 592–607, Jul. 2018.
[5] T. Caminada, “Zuggurtmodell – zykische Beanspruchug”, Vertiefungsmodul I, Fachgruppe Massivbau HSLU, Horw, 2017
[6] T. Caminada, “Normalkraft beanspruchte Betonelemente”, Vertiefungsmodul II, Fachgruppe Massivbau HSLU, Horw, 2017
[7] T. Caminada, “Gerissenes Scheibenmodell für zyklische Beanspruchungen”, Master’s Thesis, Fachgruppe Massivbau HSLU, Horw, 2018
[8] P. Marti, M. Alvarez, W. Kaufmann and V. Sigrist, “Tension Chord Model for Structural Concrete”, Structural Engineering International, vol. 8, no. 4, pp. 287–298, Nov. 1998, doi: 10.2749/101686698780488875.
[9] W. Kaufmann, “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces”, Doctoral dissertation, Institut für Baustatik und Konstruktion, ETH Zürich, Basel, 1998. doi: 10.1007/978-3-0348-7612-4.
[10] H. Seelhofer, Ebener Spannungszustand im Betonbau: Grundlagen und Anwendungen. Zürich: vdf Hochschulverl. an d. ETH, 2010.
[11] T. Pfyl and P. Marti, Versuche an stahlfaserverstärkten Stahlbetonelementen, vol. 268. 2001. [Online]. Available: https://doi.org/10.3929/ethz-a-004273447
[12] R. Koppitz, A. Kenel, and T. Keller, “Tension Chord Model Modification for Uniaxial Unloading and Reloading in Elastic and Plastic States”, Journal of Structural Engineering, vol. 140, no. 10, p. 04014077, Oct. 2014, doi: 10.1061/(ASCE)ST.1943-541X.0000999.