Ein neuer Ansatz für Schalenelemente in der Finiten Elemente Analyse – Concrete E-Learning Platform

Link to English version: A new approach for a shell element of the finite element analysis

In diesem Blogpost werde ich mich darauf konzentrieren, die Entwicklung eines neuartigen sogenannten „hybriden Machine-Learning-Finite-Elemente-Analyse“-Ansatzes (hybride ML-FEA) für Schalenelemente zu erläutern. Insbesondere werde ich dabei den Fokus darauf legen, welche Daten zur Erstellung dieses Ansatzes verwendet wurden. In meinem letzten Blogpost habe ich bereits die Motivation für die Verwendung von Machine Learning in der Finite-Elemente-Analyse für Stahlbetonkonstruktionen geschildert und ein einfaches Beispiel für ein Surrogate Model («Ersatz-Modell») eines Stahlbetonbalkens gezeigt. Kurz zusammengefasst: Um die iterative Bestimmung der Krümmung aufgrund des Moments in einem potentiell gerissenen Querschnitt eines Stahlbetonträgers zu umgehen, wurde ein neuronales Netzwerk trainiert, das diese Aufgabe ersetzen kann.

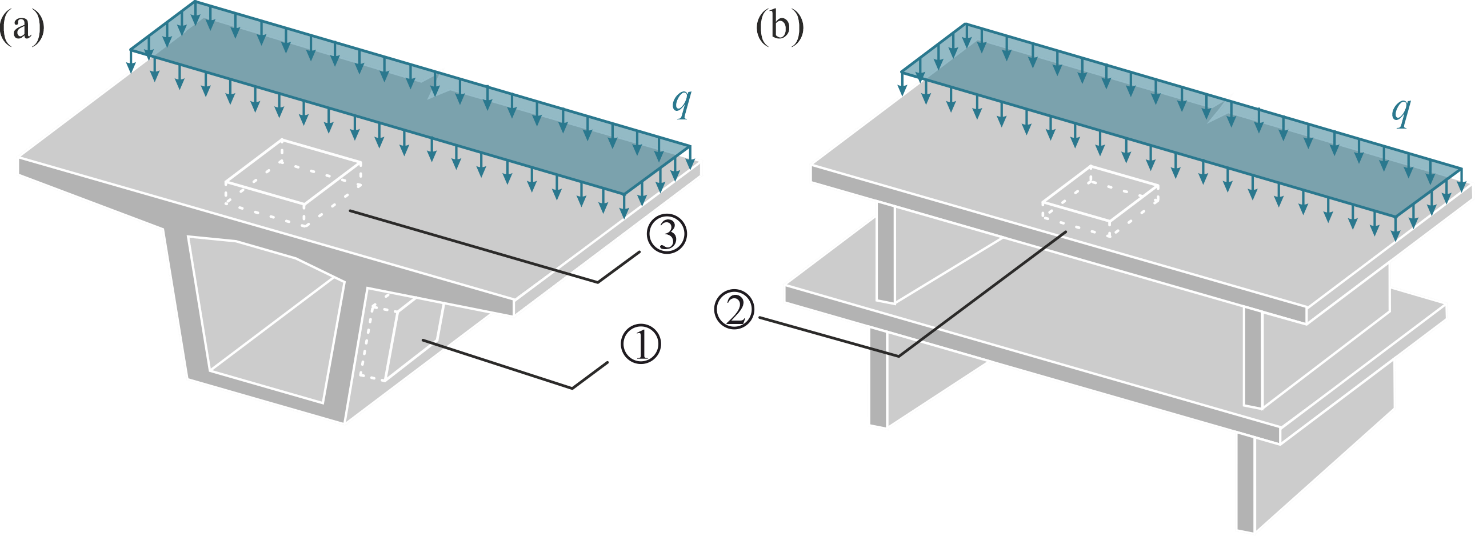
Häufig werden jedoch Stahlbetonplatten und -schalen (und nicht Stahlbetonbalken) als Bestandteile in grossen Infrastrukturbauten verwendet. Abbildung 1 zeigt drei typische Beispiele von solchen Schalenelementen in der Fahrbahnplatte oder im Steg eines Brückenträgers ((a), Nr. 1 und 3) oder in einer standartmässigen Deckenplatte ((b), Nr. 2). Es ist deshalb wichtig, die Anwendbarkeit von Machine Learning in einer schalenbasierten FEA zu untersuchen, sodass ein zweckmässiger hybrider ML-FEA Ansatz für Stahlbetonbauten erstellt werden kann, welcher als Ersatz (oder Umgehung) der standardmässigen FEA dienen kann.

Abbildung 1: Unterschiedliche mögliche Beispiele von Schalenelementen in typischen Infrastrukturbauten [1].

Im Vergleich zu anderen Machine-Learning basierten Surrogate Models, soll sich dieser Ansatz insbesondere durch das Niveau in der FEA auf dem er ansetzt hervorheben: Andere Methoden (z.B. Kuhn et al., siehe separater Blogpost) ersetzen die gesamte FEA oder versuchen durch den Ersatz von Spannungs( $\sigma$ )-Dehnungs( $\varepsilon$ )-Beziehungen auf einem Materialpunkt (z.B. Li et al., Neural Metamaterial Models) neue Materialmodelle zu entwickeln. Der hier vorgestellte hybride ML-FEA Ansatz soll jedoch für das finite Element Niveau erstellt werden können, das heisst für ein Schalenelement gültig sein.

Dies bedeutet, dass das ML Modell die Beziehung zwischen generalisierten Spannungen ( $\hat{\sigma}$ oder auch «resultierenden Schnittkräften») und generalisierten Dehnungen ( $\hat{\varepsilon}$ ) ersetzen soll. Beide bestehen aus acht Variablen wie sie für ein geschichtetes Schalenelement aus Stahlbeton verwendet werden (Abbildung 2 und Gleichung 1): Drei Membrankraft- resp. Membrandehnungskomponenten ( $n_x, n_y, n_{xy}$ resp. $\varepsilon_x, \varepsilon_y, \varepsilon_{xy}$ ), drei Momenten- resp. Krümmungskomponenten ( $m_x, m_y, m_{xy}$ resp. $\chi_x, \chi_y, \chi_{xy}$ ) und zwei Querkraft- resp. Schubdehnungskomponenten: ( $v_{xz}, v_{yz}$ resp. $\gamma_{xz}, \gamma_{yz}$ ). In Gleichung 1 entspricht $\mathbf{D}$ der generalisierten Steifigkeitsmatrix, welche den Bezug zwischen den generalisierten Dehnungen und den generalisierten Spannungen darstellt.

Abbildung 2: Schalenelement und die zugehörigen generalisierten Spannungs- und Dehnungskomponenten [1].

$\left\{\begin{matrix} n_x, n_y, n_{xy} \\ m_x, m_y, m_{xy} \\ v_{xz}, v_{yz}\end{matrix} \right\} = \left[\mathbf{D}\right]\left\{ \begin{matrix} \varepsilon_x, \varepsilon_y, \varepsilon_{xy} \\ \chi_x, \chi_y, \chi_{xy} \\ \gamma_{xz}, \gamma_{yz}\end{matrix}\right\}$

Gleichung 1: Beziehung zwischen generalisierten Spannungen und Dehnungen.

In einem ersten Beispiel der Untersuchung eines hybriden ML-FEA Ansatzes für Schalen, wird ein geschichtetes, linear-elastisches Schalenelement, basierend auf der Reissner-Mindlin Schalentheorie analysiert (Abbildung 2, Gleichung 1). Im Vergleich zu typischen Kirchhoff’schen Schalenelemente beinhalten Reissner-Mindlin-Elemente also auch Schubkomponenten und werden für dicke Schalenelemente verwendet (Gleichung 1). Aufgrund der Schichtung des Schalenelements können die individuellen Schichten, welche jeweils im ebenen Spannungszustand modelliert werden, separat analysiert werden. Während der klassischen FEA werden also zuerst die Dehnungs- und danach die Spannungszustände in jeder Schicht des Elements evaluiert. Danach werden die Spannungen über die Höhe des Elements zu den generalisierten Spannungen aufintegriert. Die lineare Elastizität vereinfacht das Problem für diesen ersten Schritt der Untersuchung und resultiert in einer geschlossenen Form für die Matrix $\mathbf{D}$ (d.h. $\mathbf{D}$ kann analytisch berechnet werden). In einem komplexeren Materialmodell, wie zum Beispiel für nichtlinearen Stahlbeton, wäre diese Matrix nicht in geschlossener Form verfügbar und müsste iterativ – je nach Dehnungszustand und entsprechendem Materialmodell – bestimmt werden (z.B. Materialmodelle, welche im gerissenen Scheibenmodell Usermat angewendet werden).

An dieser Stelle ist es wichtig zu erwähnen, dass die angenommene lineare Elastizität das Problem so fest vereinfacht, dass ein Machine Learning weder die Geschwindigkeit noch die Genauigkeit der FEA verbessern kann. Der Grund, warum dennoch ein hybrider ML-FEA Ansatz implementiert wird, liegt nur darin, die Machbarkeit eines solchen Ansatzes in einem Fall zu testen, in dem die standartmässige FEA-Lösung einfach verfügbar ist aufgrund der analytischen Lösung. In Zukunft wird das Ziel sein, diesen Ansatz auf geschichtete Scheibenelemente mit komplexeren Materialmodellen auszuweiten, wie zum Beispiel Elemente, die für nichtlineare Analysen von Stahlbeton verwendet werden.

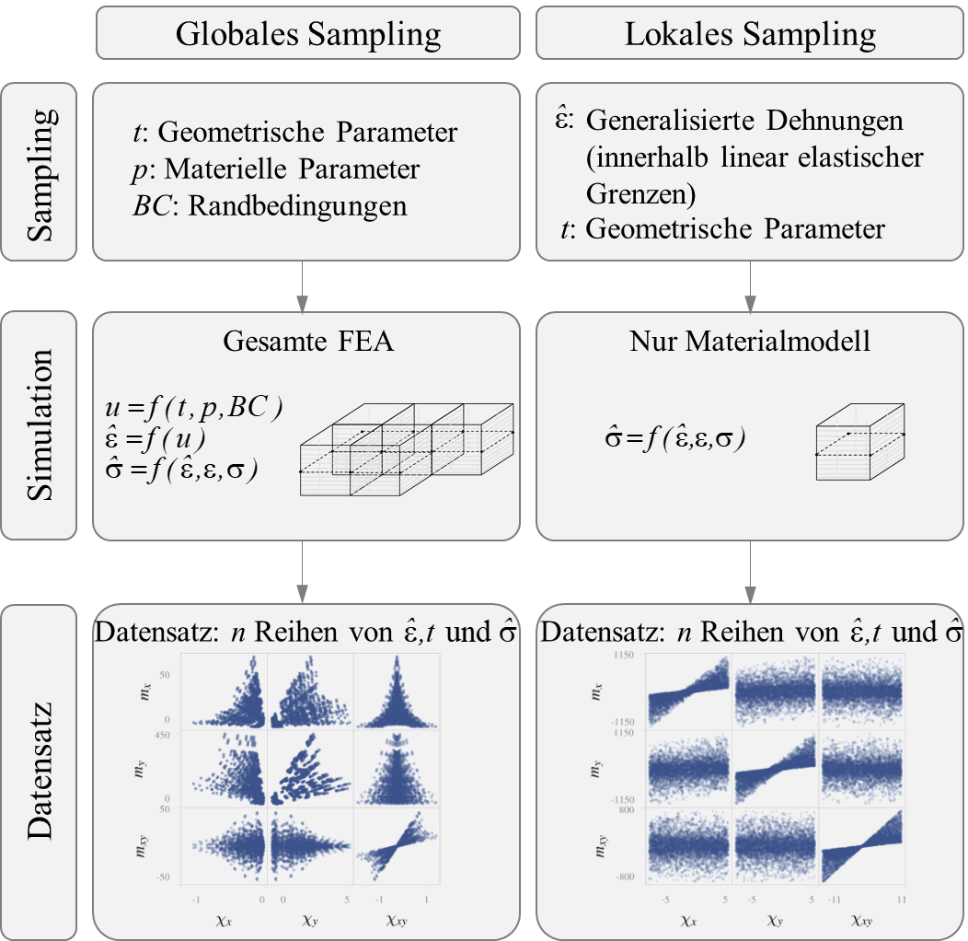
Um das ML Modell zu erstellen, braucht es zwei Hauptkomponenten: Daten und eine passende ML Architektur. In diese Blogpost möchte ich mich auf die Datenakquisition fokussieren. In diesem ersten Schritt der Untersuchung werden die Daten aus der standartmässigen FEA generiert, es handelt sich also um sogenannte «synthetische Daten». Es dauert eine Weile bis alle benötigten Daten so simuliert werden können. Sobald jedoch der Datensatz erstellt und das ML Modell trainiert ist, dauert eine Anfrage des hybriden ML-FEA Ansatzes nicht länger als eine Berechnung mit der standartmässigen FEA. Es gibt zwei Arten, wie die Daten mittels FEA simuliert werden können: Globales und lokales Sampling (Abbildung 3). In der globalen Methode werden zuerst unterschiedliche Plattencharakteristika und Randbedingungen gewählt, die mit einem Latin Hypercube Sampler (siehe auch Wikipedia) gesampelt werden. Danach werden die generalisierten Spannungen mit einer normalen FEA ermittelt. Im Gegensatz dazu werden beim lokalen Sampling direkt die generalisierten Dehnungen mit dem Latin Hypercube Sampler ermittelt. Diese müssen dann nur durch das Materialmodell geschickt werden um die generalisierten Spannungen zu bestimmen und so den gewünschten Datensatz zu erstellen. Der endgültige Datensatz besteht dann aus n Reihen von $\hat{\varepsilon}$ , $t$ , $u$ und $\hat{\sigma}$ . Obwohl diese beiden Methoden auf den ersten Blick erscheinen, als ob sie dieselben Datensätze generieren würden, beeinflusst die Sampling-Methode die Trainierbarkeit der ML Modelle massgeblich: Wie in Abbildung 3 dargestellt führt der Datensatz, der aufgrund von lokalem Sampling erstellt wurde, zu viel gleichmässiger verteilten Daten und damit zu einem viel besseren Training für ein ML Modell. Es zeigt also wieder einmal, dass jedes ML Modell nur so gut ist wie die ihm zugrunde gelegten Daten.

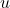Abbildung 3: Zwei unterschiedliche Sampling Methoden, welche zu unterschiedlichen Datensatzverteilungen führen. Im Bild sind nur die Daten für die Krümmungen und die Momente dargestellt. Zugehörige Schub- und Normaldehnungen wie auch Quer- und Normalkräfte wurden ebenfalls gesampelt ( $u$ : Verschiebungen; 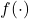$f(\cdot)$ : eine Funktion).

Vielleicht fragen Sie sich nun, warum man nicht experimentelle Daten für diese Untersuchung verwendet, sondern sich die Mühe des Samplings vom linear-elastischen Materialmodell gemacht hat. Es gibt dafür zwei Gründe: Erstens handelt es sich beim betrachteten Ansatz um ein Einführungsbeispiel, das nur für linear-elastische Bedingungen verwendet werden kann, für welche die Daten aus Experimenten schwierig zu extrahieren wären und dann doch nicht das ganze Materialverhalten abbilden würden, d.h. nur den ungerissenen Teil. Zweitens sind experimentelle Daten nur spärlich verfügbar: Als nächsten Teil des Projekts, werden zurzeit experimentelle Daten von Schalenelementtests (z.B. von Experimenten am LUSET) gesammelt, um einen Datensatz für die nichtlineare Analyse von Stahlbeton zu erstellen. Zudem besteht die Möglichkeit, dass diese Daten nicht einer so schönen Verteilung folgen, wie sie für ein gutes ML Training benötigt würden.

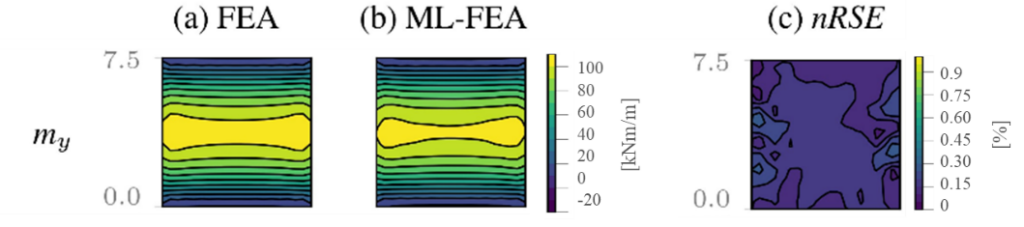
Nach dem Sampling der Daten des linear-elastischen Materialmodells wurden verschiedene physik-basierte ML Modelle getestet, um die mechanische Beziehung $D = \frac{\partial\hat{\sigma}}{\partial\hat{\varepsilon}}$ in der ML Architektur einzubetten. Ein Training mit einem Deep Operator Network führte zu den besten Vorhersagen für die generalisierten Spannungen und wurde deshalb für den linear-elastischen, hybriden ML-FEA Ansatz verwendet. Detailliertere Informationen zur gewählten ML Architektur finden Sie im Paper [1]. Das Deep Operator Network wurde dann in der FEA verwendet, wobei Abbildung 4 eine Beispielberechnung von einer Deckenplatte zeigt, welche durch Biegung in eine Richtung beansprucht ist (Beispiel 2, Abbildung 1). Diese Beispielrechnung besteht aus 100 finiten Schalenelementen (10×10). Abbildung 4 zeigt nun, dass die standartmässige FEA (a) und der hybride ML-FEA Ansatz (b), in dem jedes Schalenelement mit dem ML Modell ersetzt wurde, sehr ähnliche Resultate ergeben, was weiter durch die Fehlerberechnung (c) eines normalisierten Wurzelquadratfehlers («normalised root squared error», nRSE) hervorgehoben wird. So konnte man die Machbarkeit des hybriden ML-FEA Ansatzes im vereinfachten linear-elastischen Beispiel überprüfen.

Abbildung 4: Vergleich der standardmässigen FEA zum ML-FEA hybrid Ansatz, basierend auf der Deep Operator Network Architektur (von [1] adaptiert).

Ein Paper dazu wurde beim fib Symposium, das im Juni 2025 stattfindet, eingereicht. Dieses Paper wird hier verlinkt werden sobald es online verfügbar ist – bis dann können Sie sich gerne bei mir direkt melden, ich erläutere Ihnen gerne die weiteren Details. Bleiben Sie daran für weitere Erkenntnisse in Machine Learning für die Finite Elemente Analyse von Stahlbetontragwerken!

Vera Balmer

Literatur

[1] V. Balmer, M.A. Kraus, S. Coros, W. Kaufmann: “Training and Integrating a Machine-Learning-Based Shell Element in Reinforced Concrete Simulations”, submitted to the fib Symposium 2025, Antibes