Link zur deutschen Version: Gewindestangen aus nichtrostendem Stahl: Relaxation und Anwendung beim Vorspannen
High-strength duplex (stainless-steel) threaded rods might be a solution for external post-tensioning of structural elements in both new construction and strengthening of existing structures. However, their use in post-tensioning applications is limited due to the lack of reliable data on the relaxation of stainless-steel rods, making the estimation of relaxation relevant for their use in post-tensioning. For stainless-steel, it is even more important, as the maximum initial strain induced by tensioning is significantly lower than that of conventional prestressing steel —about 50% with respect to steel Y1860-S7—. They are limited by (i) its low yield strength ![]() < 1’000 MPa (
< 1’000 MPa (![]() > 1’000 MPa for typical steels used for post-tensioning), and (ii) the design tensile resistance of threaded rods defined in SIA 263:2013 [1] (considered as bolts):
> 1’000 MPa for typical steels used for post-tensioning), and (ii) the design tensile resistance of threaded rods defined in SIA 263:2013 [1] (considered as bolts):
(1) ![]()
where ![]() is the design tensile resistance of the threaded rod;
is the design tensile resistance of the threaded rod; ![]() the tensile strength of the threaded rod;
the tensile strength of the threaded rod; ![]() the net area of the threaded rod; and
the net area of the threaded rod; and ![]() the partial factor of resistance of cross-sections in tension (
the partial factor of resistance of cross-sections in tension (![]() = 1.25).
= 1.25).
The tensioning strain limitations play a more significant role in post-tensioned elements subject to imposed deformation (e.g. creep and shrinkage), where post-tensioning losses may reach unacceptable values. Considering a post-tensioned concrete element, Table 1 compares the post-tensioning losses in terms of strain between duplex stainless steel and Y1860 steel by using typical design and material properties values. It comes out that the post-tensioning losses of duplex stainless steel are 27%, almost double those of Y1860 steel (15%). Since high post-tensioning losses might be inadmissible according to SIA 262:2013 [2], which limits the minimum post-tensioning after losses at infinite time to 0.45·![]() , it is essential to control the post-tensioning losses by knowing the relaxation of the duplex threaded rods and exploiting the tensioning strain (
, it is essential to control the post-tensioning losses by knowing the relaxation of the duplex threaded rods and exploiting the tensioning strain (![]() ≥ 0.75·
≥ 0.75·![]() , i.e., exceeding the design tensile strength according to Eq. (1).
, i.e., exceeding the design tensile strength according to Eq. (1). ![]() is the initial tensioning stress).
is the initial tensioning stress).
| Concrete | |||||
| 30 | Modulus of elasticity | ||||
| 0.35 | Shrinkage | ||||
| 2.0 | Creep coefficient | ||||
| 5.0 | Initial stresses | ||||
| 0.17 | Initial strain | ||||
| 0.33 | Long-term strain increment | ||||
| Duplex stainless steel | Steel Y1860-S7 | ||||
| 160 | 195 | Modulus of elasticity | |||
| 800 | 1860 | Ultimate tensile strength / Characteristic tensile strength | |||
| 700 | 1640 | Yield strength / 0.1% proof stress (characteristic) | |||
| 1.25 | 1.15 | Partial safety factor | |||
| 576 | 1617 | Design value of tensile strength | |||
| 560 | 1302 | Initial prestress | |||
| 3.50 | 6.68 | Initial strain | |||
| 7.5% | 5% | Relaxation (prestress loss ratio) | |||
| 27% | 15% | ||||
| (1) | |||||
| (2) | |||||
To assess the potential of high-strength duplex (stainless-steel) threaded rods for post-tensioning, this post presents the results of an experimental campaign focused on the relaxation behaviour of M24, M27, and M30 rods. Relaxation was measured over 1’000 hours in accordance with the ISO 15630-3:2019 [3] standard. The study also evaluated whether theoretical models for prestressing steel could reliably predict long-term relaxation using shorter 120-hour tests on duplex threaded rods.
The experimental camping was conducted at the ETH Zurich structural lab in 2023, including nine relaxation tests (three specimens per rod size) on M24, M27 and M30 duplex threaded rods. Additional tensile tests (not shown here in detail) were performed on rods with no prior loading history and on rods after relaxation tests to assess changes in the mechanical properties of the material.
Experimental campaign
Table 2 summarises the designation and characteristics of the specimens, which consist of high-strength duplex (stainless steel) threaded rods (EN 1.44621Material properties of high-strength duplex EN 1.4462, according to the technical documentation of Leviat AG products [4], are as follows: Yield strength: ![]() ≥ 700 MPa, tensile strength:
≥ 700 MPa, tensile strength: ![]() ≥ 900 MPa and ultimate tensile strain:
≥ 900 MPa and ultimate tensile strain: ![]() = 15‰ – 30‰). Duplex rods with full-length threads were selected to ensure a constant stress-strain behaviour along the specimen. Higher prestressing force (or elongation) is achieved in full-length threaded rods compared to those only threaded in the anchorage zone (the threaded zones govern the maximum tensioning stress, not exploiting the capacity of the non-threaded zones).
= 15‰ – 30‰). Duplex rods with full-length threads were selected to ensure a constant stress-strain behaviour along the specimen. Higher prestressing force (or elongation) is achieved in full-length threaded rods compared to those only threaded in the anchorage zone (the threaded zones govern the maximum tensioning stress, not exploiting the capacity of the non-threaded zones).
| ID (1) | Size | Material | [mm] | Cross-section (2) (effective) [mm2] | Total length [mm] | [kN] |
| SX-M24-r | M24 | EN 1.4462 | 24 | 353 | 1800 | 229 |
| SX-M27-r | M27 | EN 1.4462 | 27 | 459 | 1800 | 297 |
| SX-M30-r | M30 | EN 1.4462 | 30 | 561 | 1800 | 364 |
| (1) SX: Specimen S1, S2 and S3; r: “relaxation tests” | ||||||
| (2) According to the technical documentation of the product [4] | ||||||
| (3) By applying Eq. (1) | ||||||
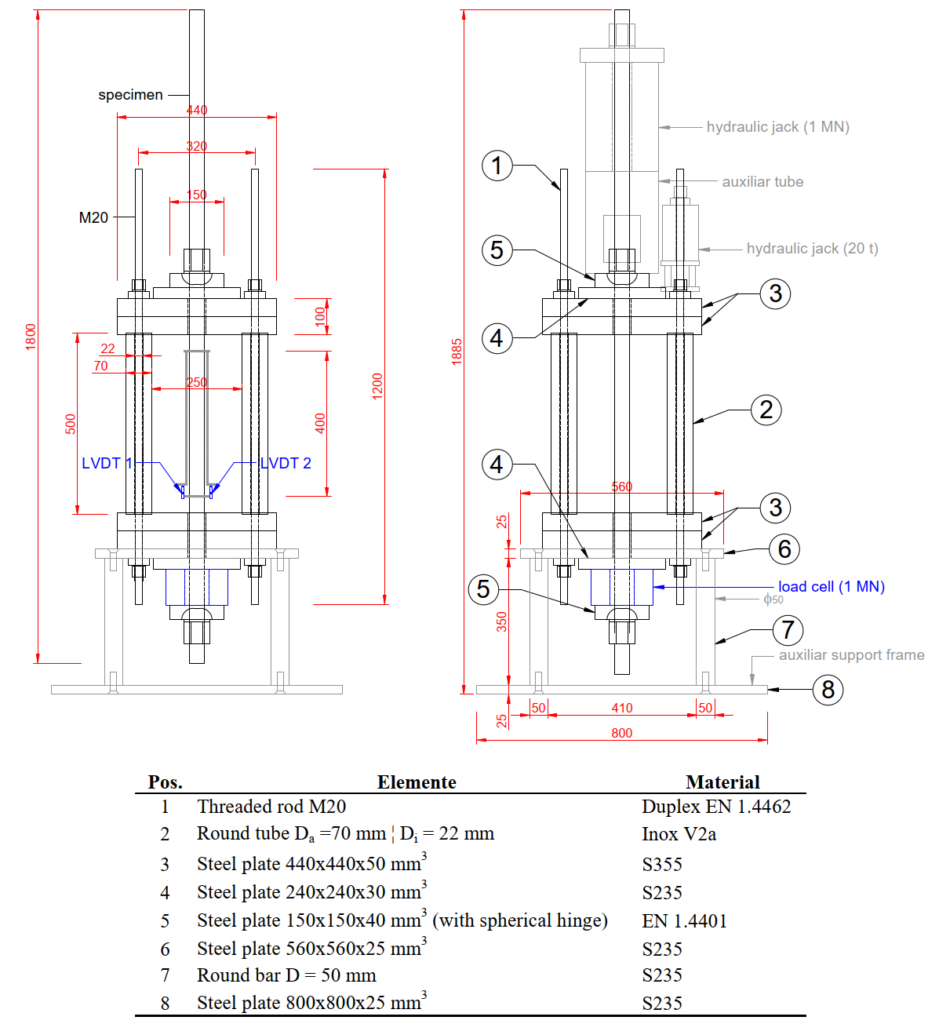
Figure 1 provides an overview of the test rig designed at ETH Zürich to conduct the relaxation tests on threaded rods according to ISO 15630-3:2019. The test rig consists of a main frame (pos. 1, 2 and 3), a support frame (pos. 6, 7 and 8), anchorage plates (pos. 4 and 5) and measuring equipment (two LVDTs and one load cell).
Relaxation at 1’000 hours
The relaxation tests of duplex threaded rods (M24, M27, and M30) were conducted at 1’000 hours with an initial tensioning stress (![]() ) ranging between 0.72 and 0.82 of the average tensile strength (
) ranging between 0.72 and 0.82 of the average tensile strength (![]() ) obtained from the tensile tests performed on rods with no prior loading history (see the average for
) obtained from the tensile tests performed on rods with no prior loading history (see the average for ![]() in Table 3). The initial stress,
in Table 3). The initial stress, ![]() , varied between the specimens because, during the tensioning process, it was difficult to precisely control (but only estimate) the initial tensioning force (
, varied between the specimens because, during the tensioning process, it was difficult to precisely control (but only estimate) the initial tensioning force (![]() ), as there was an uncontrolled loss of force upon releasing the jack after the tightening of the nut.
), as there was an uncontrolled loss of force upon releasing the jack after the tightening of the nut.
Figure 2 illustrates the experimental stresses, relaxation, and deformation variation over time for duplex threaded rods M24, M27, and M30. Relaxation (considered positive) — defined as stress losses (![]() /
/ ![]() ) — is depicted as the change in stress relative to the initial tensioning stress. The stress losses are shown by solid lines in graphs a.2 (M24), b.2 (M27), and c.2 (M30) in Figure 2.
) — is depicted as the change in stress relative to the initial tensioning stress. The stress losses are shown by solid lines in graphs a.2 (M24), b.2 (M27), and c.2 (M30) in Figure 2.
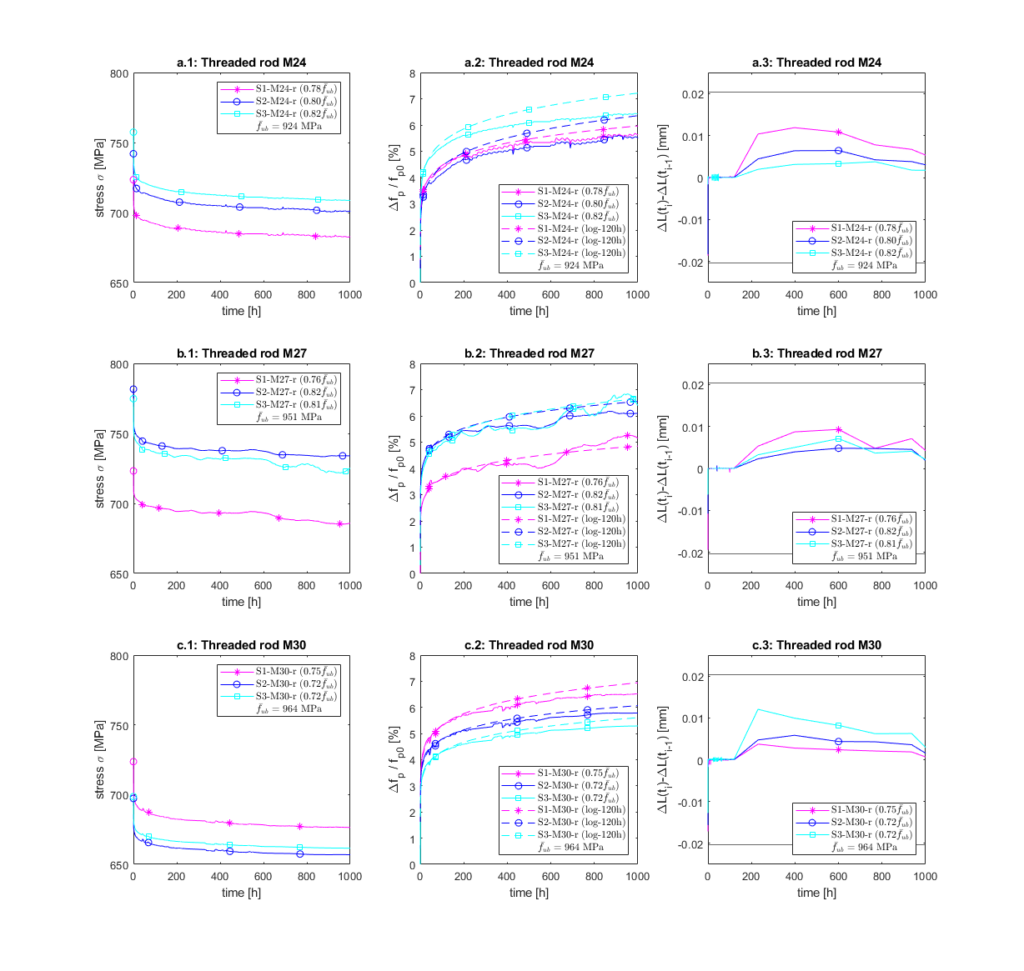
The deformation variation, ![]() , shown in Figure 2 (a.3, b.3 and c.3), is monitored to ensure that the imposed deformation remains constant within the limits established in [3], “The variation of
, shown in Figure 2 (a.3, b.3 and c.3), is monitored to ensure that the imposed deformation remains constant within the limits established in [3], “The variation of ![]() shall not exceed 5 × 10−5
shall not exceed 5 × 10−5 ![]() between two consecutive force measurements“. In the relaxation tests, the reference length
between two consecutive force measurements“. In the relaxation tests, the reference length ![]() is 405 mm; thus, the maximum admissible variation between two consecutive force measurements is ±0.0203 mm. The reference force measurements are indicated in Table 2 of reference [3]. The most significant variations (within permissible values) occur instantaneously in the first seconds, attributed to small slippages of the force holding nuts . The remaining variations are well within tolerance limits (±0.0203 mm), confirming the sufficient stiffness of the testing rigs for conducting relaxation tests.
is 405 mm; thus, the maximum admissible variation between two consecutive force measurements is ±0.0203 mm. The reference force measurements are indicated in Table 2 of reference [3]. The most significant variations (within permissible values) occur instantaneously in the first seconds, attributed to small slippages of the force holding nuts . The remaining variations are well within tolerance limits (±0.0203 mm), confirming the sufficient stiffness of the testing rigs for conducting relaxation tests.
Table 3 summarises the initial (![]() ) stresses and the relaxation (prestress loss ratio),
) stresses and the relaxation (prestress loss ratio), ![]() /
/![]() , at 10 minutes, 120 hours, and 1’000 hours of duplex threaded rods M24, M27, and M30, according to Figure 2. The average relaxation at 1’000 hours for the three metrics of threaded rods (M24, M27, and M30) is around 6% for initial tensioning stresses ranging from approximately 0.70 to 0.85 times
, at 10 minutes, 120 hours, and 1’000 hours of duplex threaded rods M24, M27, and M30, according to Figure 2. The average relaxation at 1’000 hours for the three metrics of threaded rods (M24, M27, and M30) is around 6% for initial tensioning stresses ranging from approximately 0.70 to 0.85 times ![]() . The evolution of relaxation over time resembles a logarithmic growth, with the most significant development occurring within the first 120 hours. About 30% and 80% of the relaxation at 1’000 hours occur within the first 10 minutes and 120 hours, respectively.
. The evolution of relaxation over time resembles a logarithmic growth, with the most significant development occurring within the first 120 hours. About 30% and 80% of the relaxation at 1’000 hours occur within the first 10 minutes and 120 hours, respectively.
| Specimen | ||||||||
| [MPa] | [MPa] | [MPa] | [MPa] | [-] | [%] | [%] | [%] | |
| S1-M24-r | 911 | 716 | 797 | 725 | 0.78 | 1.9 | 4.5 | 5.6 |
| S2-M24-r | 911 | 738 | 791 | 747 | 0.80 | 1.4 | 4.3 | 5.5 |
| S3-M24-r | 950 | 731 | 809 | 757 | 0.82 | 2.3 | 5.3 | 6.4 |
| Avg. M24 | 924 | 728 | 799 | 743 | 0.80 | 1.9 | 4.7 | 5.8 |
| S1-M27-r | 941 | 713 | 809 | 723 | 0.76 | 1.6 | 3.7 | 5.2 |
| S2-M27-r | 970 | 720 | – | 782 | 0.82 | 2.6 | 5.2 | 6.1 |
| S3-M27-r | 942 | 709 | 855 | 775 | 0.81 | 2.3 | 5.0 | 6.4 |
| Avg. M27 | 951 | 714 | 832 | 760 | 0.80 | 2.1 | 4.6 | 5.9 |
| S1-M30-r | 996 | 783 | – | 724 | 0.75 | 1.9 | 5.4 | 6.5 |
| S2-M30-r | 938 | 777 | 855 | 697 | 0.72 | 1.8 | 4.9 | 5.8 |
| S3-M30-r | 957 | 794 | 830 | 699 | 0.72 | 1.5 | 4.4 | 5.3 |
| Avg. M30 | 964 | 785 | 842 | 706 | 0.73 | 1.7 | 4.9 | 5.9 |
| (1) According to the direct tensile tests performed on rods with no prior loading history (2) According to the direct tensile tests performed after relaxation tests | ||||||||
Relaxation at 120 hours and theoretical estimations at 1’000 h
As an alternative to the 1’000-hour relaxation tests, ISO 15630-3 [3] allows carrying out the tests for a reduced period of at least 120 hours. In this case, the relaxation at 1’000 hours can be extrapolated from the following semi-empirical equation:
(2) ![]()
where ![]() /
/![]() is the relaxation, generally expressed in percent;
is the relaxation, generally expressed in percent; ![]() is time, expressed in hours, and
is time, expressed in hours, and ![]() and
and ![]() are coefficients. The coefficients
are coefficients. The coefficients ![]() and
and ![]() are obtained from logarithmic regression of experimental results from the first 120 hours. Figure 2 (a2, b2, and c2) shows the relaxation obtained from the semi-empirical Eq. (2), log-120h (dotted lines). It is observed that the log-120h curves correlate well with the experimental curves up to about 200 hours, but tend to overestimate relaxation at 1’000 hours.
are obtained from logarithmic regression of experimental results from the first 120 hours. Figure 2 (a2, b2, and c2) shows the relaxation obtained from the semi-empirical Eq. (2), log-120h (dotted lines). It is observed that the log-120h curves correlate well with the experimental curves up to about 200 hours, but tend to overestimate relaxation at 1’000 hours.
The relaxation values at 1’000 hours, derived from the semi-empirical Eq. (2) and compared with experimentally obtained values, are outlined in Table 4. Notably, the 1’000predicted values tends to be slightly higher, exhibiting variations of 11.3%, 1.9%, and 5.8% (average values) for rods M24, M27, and M30, respectively. These differences remain within acceptable limits and are on the safe side to be considered in the post-tensioning design in structures.
| Specimen | |||
| exp. | Eq. (2) | ||
| [%] | [%] | [%] | |
| S1-M24-r | 5.61 | 5.96 | 6.2 |
| S2-M24-r | 5.51 | 6.36 | 15.4 |
| S3-M24-r | 6.42 | 7.21 | 12.3 |
| x̄r | 5.85 | 6.51 | 11.3 |
| S1-M27-r | 5.15 | 4.85 | -5.8 |
| S2-M27-r | 6.10 | 6.55 | 7.4 |
| S3-M27-r | 6.39 | 6.65 | 4.1 |
| x̄r | 5.88 | 6.02 | 1.9 |
| S1-M30-r | 6.52 | 6.94 | 6.4 |
| S2-M30-r | 5.79 | 6.07 | 4.8 |
| S3-M30-r | 5.29 | 5.61 | 6.0 |
| x̄r | 5.87 | 6.21 | 5.8 |
Discussion and recommendations
Relaxation tests of duplex threaded rods resulted in average losses of around 6% at 1’000 hours, with their evolution over time resembling a logarithmic growth. The most significant development occurs within the initial 120 hours. Approximately 30% and 80% of the relaxation at 1’000 hours takes place within the first 10 minutes and 120 hours, respectively. However, based on comparisons made at the 10-minute mark during direct tension relaxation tests, it was observed that threaded rods previously subjected to loading and unloading cycles (in this experimental campaign, due to the relaxation tests themselves) exhibited 50% reduction in relaxation compared to rods with no prior loading history. This effect resulted in a 15% reduction in relaxation for preloaded duplex threaded rods at 1’000 hours. It is important to note that the results of the direct tension tests are not presented in this post.
In order to carry out an experimental campaign with the highest possible initial stresses in the threaded rods —so that their behaviour could potentially represent an application in the post-tensioning of structures—, these stresses were maximized. As a result, the rods were subjected to initial stress levels exceeding the minimum yield strength specified in the product’s technical documentation [4] (![]() > 700 MPa). Additionally, the loading and unloading process caused by the relaxation tests increased the yield strength of the threaded rods by at least 7% compared to the direct tensile tests on rods with no prior loading history (see Table 3), i.e., a minimum increase of 13% compared to the minimum yield strength given in [4]. It should be noted that the stress-strain curve of stainless steels shows non-linear behaviour even in the service range, resulting in a lower modulus of elasticity according to standardised estimation criteria.
> 700 MPa). Additionally, the loading and unloading process caused by the relaxation tests increased the yield strength of the threaded rods by at least 7% compared to the direct tensile tests on rods with no prior loading history (see Table 3), i.e., a minimum increase of 13% compared to the minimum yield strength given in [4]. It should be noted that the stress-strain curve of stainless steels shows non-linear behaviour even in the service range, resulting in a lower modulus of elasticity according to standardised estimation criteria.
Moreover, the average initial tensioning stresses were 0.78 times the average tensile strength of all series (![]() ), i.e.
), i.e. ![]() = 736 MPa, which is higher than the design tensile strength, fsd = 576 MPa (Eq. (1)), considering
= 736 MPa, which is higher than the design tensile strength, fsd = 576 MPa (Eq. (1)), considering ![]() = 800 MPa (minimum tensile strength according to [4]).
= 800 MPa (minimum tensile strength according to [4]).
By redoing the calculations for the example presented in Table 1, considering an initial post-tensioning stress of ![]() = 760 MPa (approximately 0.80 times the average strength of all series,
= 760 MPa (approximately 0.80 times the average strength of all series, ![]() ) and an infinite time relaxation of 6%, the total post-tensioning losses are found to be 20%, in comparison to the 27% losses obtained in the preliminary calculations (Table 1). Post-tensioning losses around 20% are generally considered acceptable in the design of post-tensioned structures. It should be noted that the limitation of the design tensile strength given in Eq. (1) has been ignored, and the minimum yield strength defined by the technical documentation of the products [4] is exceeded in this new estimation.
) and an infinite time relaxation of 6%, the total post-tensioning losses are found to be 20%, in comparison to the 27% losses obtained in the preliminary calculations (Table 1). Post-tensioning losses around 20% are generally considered acceptable in the design of post-tensioned structures. It should be noted that the limitation of the design tensile strength given in Eq. (1) has been ignored, and the minimum yield strength defined by the technical documentation of the products [4] is exceeded in this new estimation.
However, their use is currently limited by their low yield strength, the design tensile strength according to SIA 263:2013 [2] (threaded rods considered as bolts) and the uncertainty of relaxation. Therefore, some recommendations or actions are listed below to overcome the limitations and promote the use of duplex threaded rods for external post-tensioning:
- By subjecting the threaded rods to a loading and unloading process (0.80…0.90 times the tensile strength,
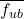 ) before the post-tensioning operations. This approach ensures an elastic behaviour during the post-tensioning phase, mitigating relaxation effects and enabling more precise tensioning control through elastic deformations.
) before the post-tensioning operations. This approach ensures an elastic behaviour during the post-tensioning phase, mitigating relaxation effects and enabling more precise tensioning control through elastic deformations. - Ideally, duplex threaded rod products destined for post-tensioning should undergo a preloading process at the manufacturing facility. Furthermore, the technical documentation should define more precisely the mechanical properties of the product, including the recommended values of initial stress for post-tensioning (0.70…0.85·
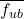 ) and their corresponding estimated relaxation.
) and their corresponding estimated relaxation. - Revision of the applicability of the design tensile strength estimation defined in SIA 263:2013 for duplex threaded rods destined for post-tensioning applications.
Please note that the recommendations and conclusions provided are derived from an experimental campaign limited to a small number of specimens. Therefore, these findings are preliminary, and a more extensive experimental campaign is needed to establish a more certain value of relaxation as a function of stress level and threaded rod diameter, and the influence of preload on the mechanical behaviour of the material.
Alejandro Giraldo Soto
References
- Schweizerischer Ingenieur- und Architektenverein (SIA), SIA 263: Stahlbau. Zürich: SIA, 2013.
- Schweizerischer Ingenieur- und Architektenverein (SIA), SIA 262: Betonbau. Zürich: SIA, 2013.
- ISO, “ISO 15630-3 Steel for the reinforcement and prestressing of concrete (Test methods) Part 3: Prestressing steel,” Geneva, Switzerland, 2019.
- Leviat AG, “Nichtrostende Bewehrungen für die Bauindustrie.” Jun. 2019.