Link to the English version: Finite-Element-Method in Structural Engineering
Grundprinzip und Anwendungsgebiete der FEM
Computerunterstützte Berechnungsmethoden – allen voran die Finite Elemente Methode (FEM) – haben sich in den letzten Jahrzehnten zu einem unverzichtbaren Werkzeug im Ingenieurwesen gemacht. Mit der Entwicklung der FEM können alltägliche Rechen- und Routineaufgaben automatisiert und ohne Flüchtigkeitsfehler durchgeführt werden. Damit ist (zumindest ein Teil) von Konrad Zuse’s [1] Traum von der Übernahme “lästiger” Aufgaben durch eine vollautomatisierte Rechenmaschine Wirklichkeit geworden. Die Aufgabe vom Ingenieur hat sich also vom Rechnen hin zur Modellbildung und Resultatinterpretation verlagert, für die jedoch die zugrundegelegten Theorien und Methoden bewusst und richtig angewendet werden müssen. Damit ist die Kunst der Baustatik nicht überflüssig geworden, sondern im Gegenteil, anspruchsvoller und interessanter.

Ganz allgemein gesprochen liefert die FEM eine numerische Näherungslösung für alle Aufgaben, die mathematisch mit partiellen Differentialgleichungen darstellbar sind, für die keine geschlossenen Lösungen vorliegen. Etwas vereinfachter ausgedrückt werden in der FEM komplexe Systeme (Tragwerke) in Komponenten (finite Elemente) aufgeteilt und mathematisch zu einem Gesamtmodell verknüpft. Sind die mechanischen Eigenschaften (Steifigkeiten) der einzelnen Elemente, durch eine im Rahmen der ausgewählten strukturmechanischen Modellierung vorgegebenen Beziehungen zwischen Spannungen und Verzerrungen bekannt, lassen sich unter gegebenen Einwirkungen und Randbedingungen (Lagerung) die Auswirkungen (z.B. Schnittkräfte, Verformungen, usw.) am Gesamtmodell ermitteln.
Für die alltäglichen Aufgaben der Bauingenieure/innen kommt meistens die linear-elastische FEM zum Einsatz, wobei ein linearer Zusammenhang zwischen den Spannungen und Verzerrungen vorausgesetzt wird. Die FEM liefert dabei z.B. die Schnittkräfte für die Bemessung eines Bauteils auf Basis von ideal-plastischen Modellvorstellungen. In Spezialfällen z.B. bei der statischen Überprüfung von bestehenden Tragwerken kommt immer öfters die (materielle [2]) nichtlineare FEM zur Anwendung. Dabei wird ein nichtlinearer Zusammenhang zwischen den Spannungen und Verzerrungen angesetzt, womit Aussagen zum Last-Verformungsverhalten, der Rissbildung und der damit einhergehenden Schnittkraftumlagerung möglich sind. Damit lassen sich gegenüber herkömmlichen Berechnungsmethoden Traglastreserven identifizieren und effizientere Tragwerke erstellten oder im Idealfall teure Verstärkungsmassnahmen bei der statischen Ertüchtigung verhindern. Ist die reine Anwendung solcher nichtlinearer FEM-Programme dank der Entwicklung von benutzerfreundlichen Oberflächen heutzutage relativ einfach, umso komplexer gestaltet sich die Frage um die Wahl der zur vorliegenden Problemstellung passenden (nichtlinearen) Material- und Strukturmodellierung. Die Modellvorstellungen und deren Grenzen sowie die Eigenheiten einer NLFE Berechnung (z.B. Divergenzen) sollten im Detail verstanden werden. Die Vermittlung dieses Wissens ist eine zentrale Herausforderung für uns als Lehr- und Forschungsinstitut.
Geschichtlicher Abriss der Finite Elemente Methode
Im Allgemeinen geht die Entwicklung der FEM nicht auf eine einzige Person oder ein einzelnes Fachgebiet zurück, sondern hat bis heute einen stark interdisziplinären Charakter mit Aspekten aus der Mathematik, der Mechanik, dem Ingenieurwesen und der Informatik. Die Entwicklung der FEM begann in den 1950er Jahren und wurde durch die Pionierarbeiten von J. Argyris an der Universität Stuttgart, R.L. Taylor oder R. Clough an der Universität von Kalifornien, Berkley und O.C. Zienkiewicz von der Universität von Wales geprägt (alles ausgebildete Bauingenieure!). Ab den 1960er Jahren nahm die Entwicklung mit der ersten internationalen FEM Konferenz 1965 und mit dem ersten Standardwerk 1967 von Zienkiewicz mit dem Titel “The Finite Element Method in Structural and Continuum Mechanics” richtig Fahrt auf.

Die Anwendung der FEM auf Stahlbetonstrukturen begann Ende der 1960er mit den Arbeiten von Ngeo and Scordelis 1967 and Rashid 1968. Seit daher wurden unzählige Publikationen und Bücher mit den theoretischen Grundlagen, Anwendungsfällen und Richtlinien publiziert (siehe FIB Bulletin 45 2008). Die ersten FEM-Programme wurden an Universitäten entwickelt und ab den 1970er zu kommerziellen FE-Paketen mit erhöhter Benutzerfreundlichkeit weiterentwickelt (Ansys, Abaqus, ATENA, Diana). Dabei entstanden eine Vielzahl von verschieden Elementtypen (1D bis 3D) und diverse mathematische Lösungsalgorithmen für die Orts- und Zeitdiskretisierung des vorliegenden Problems. Eine Vorreiterrolle in der Entwicklung von nichtlinearen Materialmodellen für Stahlbeton und deren Implementierung in entsprechende FEM-Programme nahmen dabei D. Mitchel, M.P. Collins und F. J. Vecchio von der Universität in Toronto in den 1980er Jahren ein (Entwicklung der Druckfeldmodelle und deren Implementierung in die Software VecTor). Heutzutage ist die FEM eines der am meist verbreiteten numerischen Lösungsverfahren für unterschiedlichste physikalische Aufgabenstellungen im Bereich aller Ingenieurswissenschaften bis hin zu Wettervorhersagen. Desto stolzer können wir sein, dass Bauingenieure einen signifikanten Beitrag bei der Entwicklung der FEM lieferten.
NLFE-Tools an der Professur für Massiv- und Brückenbau
Wir von der Professur für Massiv- und Brückenbau konzentrieren uns auf die Entwicklung von nichtlinearen Materialmodellen und deren Implementierung in numerische Methoden, wie eben der FEM. In den letzten Jahren wurden an der Professur für Massiv- und Brückenbau verschiedene Tools zur nichtlinearen FEM Analyse von Bauteilen aus Stahlbeton und Mauerwerk entwickelt:
Die Compatiable Stress Field Method (CSFM) eignet sich für die detaillierte Analyse von einzelnen, eben beanspruchten Stahlbetonbauteilen eines Gesamttragwerkes (z.B. Rahmenecken oder Längsträger einer Hohlkastenbrücken wie in Abbildung 3 ersichtlich). Das CSFM basiert im Wesentlichen auf der Implementierung des Zuggurtmodelles in das FE-Programm Idea StatiCa Detail.
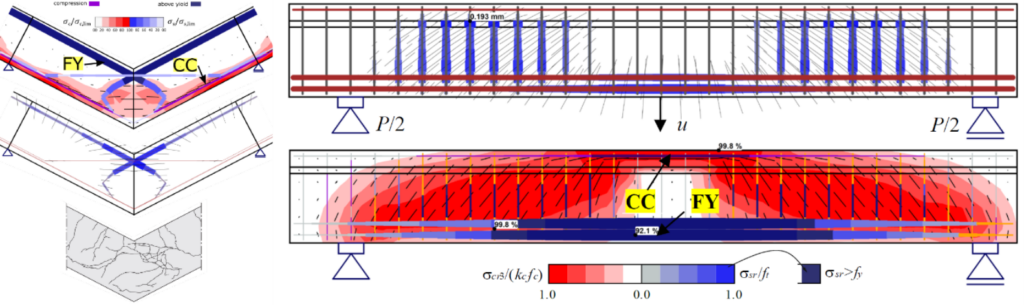
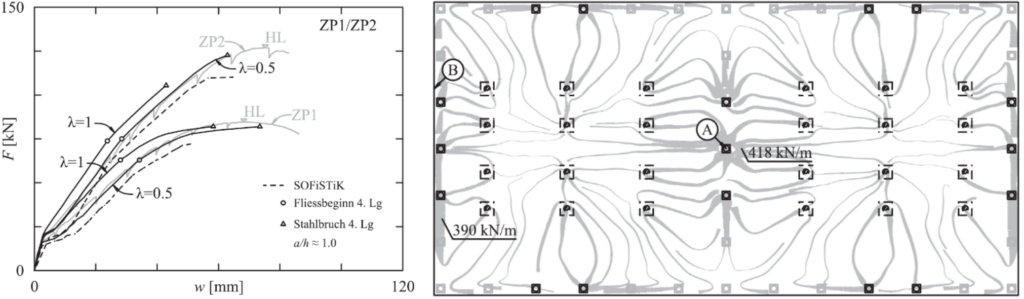
Das CMM-Usermat beinhaltet im Wesentlichen die Implementierung des durch Prof. Dr. Walter Kaufmann entwickelten Cracked Membrane Model (gerissenes Scheibenmodell) als user-defined material (Usermat) in das FEM-Programm ANSYS Mechanical APDL. In Kombination mit dem Schichtenmodell lassen sich damit komplexe Schalentragwerke (kombinierte Platten- und Scheibentragwirkung) aus Stahlbeton untersuchen (siehe Abbildung 4).
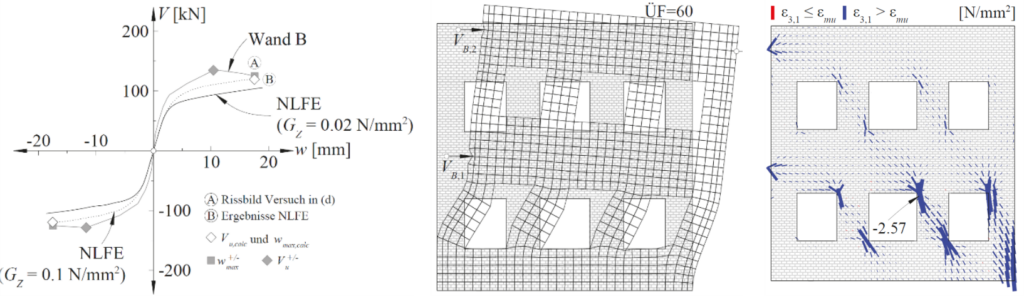
Mit dem URM-Usermat lässt sich das nichtlineare Tragverhalten von unbewehrten Mauerwerksstrukturen untersuchen (siehe Abbildung 5). Das URM-Usermat basiert auf der Implementierung erweiterter Bruchbedingungen von Ganz (welche in den 1980er an der ETH Zürich entwickelt und heute immer noch als Grundlage für die Bemessung von Mauerwerk verwendet werden) als user-defined material in das FEM-Programm ANSYS Mechanical APDL. In Kombination mit dem CMM-Usermat lässt sich das komplexe Tragverhalten von Mischtragwerken aus Stahlbeton und Mauerwerk untersuchen (siehe Abbildung 6).
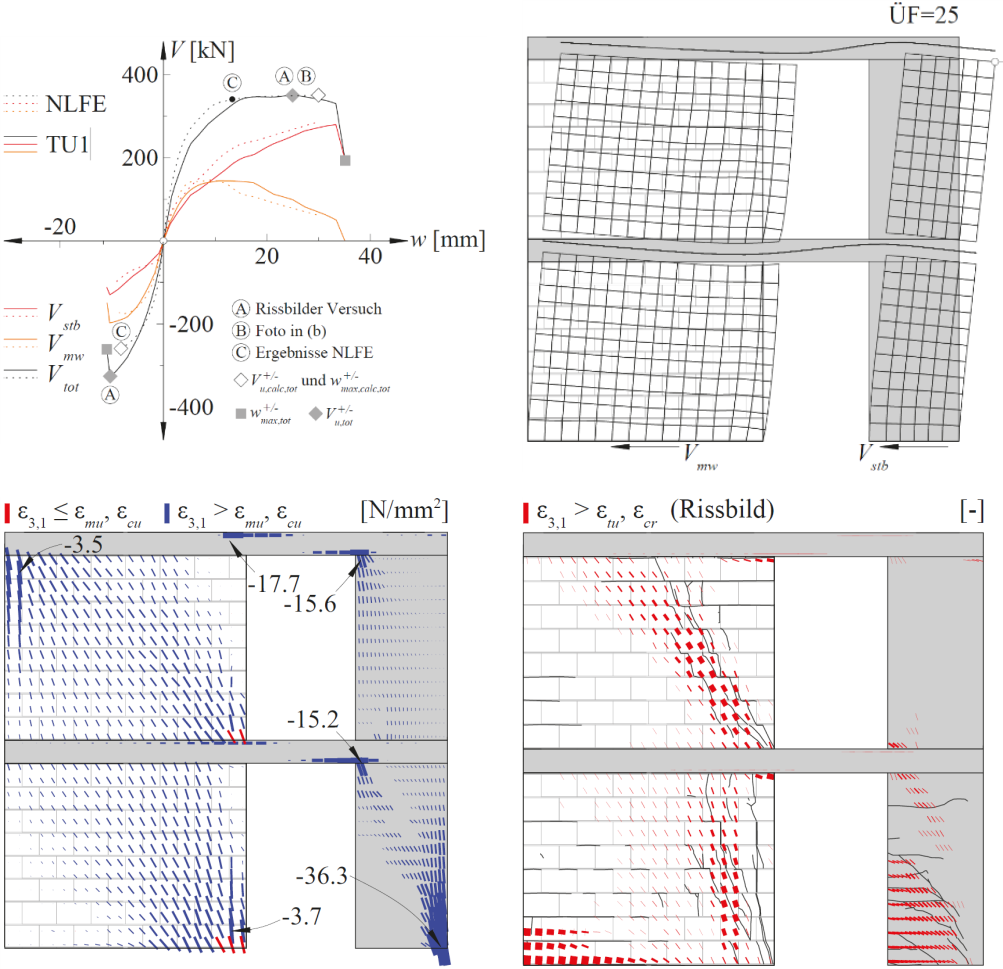
Allen NLFE-Tools gemeinsam ist, dass die Materialmodelle – auf Basis von mechanisch konsistenten Zusammenhängen – die wesentlichen Eigenschaften des Tragverhaltens von Stahlbeton bzw. Mauerwerk berücksichtigen. Zudem werden nur wenige, physikalisch klar definierte Inputparameter benötigt, welche bei der Bemessung oder der statischen Beurteilung von Tragwerken bekannt sind. Damit eignen sich die NLFE-Tools hervorragend für die Anwendung in der Baupraxis.
Aktuelle Entwicklungen
Die NLFE-Tools werden aktuell in die StrucEng Library implementiert, welche an der Professur für Massiv- und Brückenbau entwickelte wird. Die StrucEng Library ist eine OpenSource Software, mit welcher computergestützte Berechnungen von Tragsystemen aus Stahlbeton und Mauerwerk durchgeführt werden können. Dabei stehen neben den nichtlinearen Materialmodellen verschiedene weitere Materialmodelle zur Verfügung, welche das gesamte Spektrum vom Tragwerksentwurf über die Bemessung mit linear-elastischen ideal-plastischen Modellvorstellung abdecken. Die StrucEng Library soll in Zukunft im OpenSource Format zur Verfügung gestellt werden, womit die entsprechenden Modellvorstellungen von praxistätigen Ingenieuren/innen unter Verwendung einer benutzerfreundlichen Oberfläche frei verwendet werden können. Zudem werden in diversen Projekten die nichtlinearen Materialmodelle weiterentwickelt (z.B Korrosion, faserbewehrte Bauteile, etc.). In Zukunft werden zudem Lehrveranstaltungen und Weiterbildungsangebote im Bereich der numerischen Modellierung von Stahlbeton- und Mauerwerkstrukturen an der Professur für Massiv- und Brückenbau angeboten. Mit diesem besonderen Fokus in Lehre und Forschung auf die numerische Modellierung sind wir davon überzeugt, dass die angehenden Bauingenieure/innen fit für die zukünftigen Herausforderungen sind.
[1] Konrad Ernst Otto Zuse war ein deutscher Bauingieneur (!), Erfinder und Unternehmern. Mit seiner Entwicklung der Z3 im Jahre 1941 baute Zuse den ersten funktionsfähigken Computer der Welt.
[2] Im Rahmen diese Blogbeitragens wird immer von materiellen Nichtlinearität gesprochen. Des weiteren gibt es noch die geometrische Nichtlinearitäten (Berechnungen 2. Ordnung), welche über den P-Delta Effekt berücksichtigt werden.
Marius Weber
Kommentieren Sie diesen Beitrag auf LinkedIn oder Instagram